改进的抗差UKF在AUV水下声学导航中的应用

王君婷，王振杰，2

(1.中国石油大学(华东)，山东 青岛 266580；2.海洋国家实验室 海洋矿产资源评价与探测技术功能实验室，山东 青岛 266071)

0 引言

伴随着水声通信、能源、控制和导航技术的发展，自主式水下航行器(autonomous underwater vehicle，AUV)广泛应用于海上预警、水下搜索、海洋资源勘探、海底地形地貌调查与水下环境监测等领域[1]。高精度的导航系统是AUV实现自主导航的关键技术，已有的AUV导航技术包括惯性导航、声学导航以及地球物理导航[2]。随着近年来声学定位技术的迅速发展，声学导航克服了惯性导航中误差会随着时间积累的缺点，广泛应用于AUV导航系统中。水声定位技术可分为长基线定位(long baseline，LBL)、短基线定位(short baseline，SBL)和超短基线定位(ultra short baseline，USBL)。本文基于长基线定位系统进行AUV位置解算的无迹卡尔曼滤波(unscented Kalman filter，UKF)滤波算法研究。

常见的AUV导航滤波方法有拓展卡尔曼滤波算法(extended Kalman filter，EKF)、无迹卡尔曼滤波算法(unscented Kalman filter，UKF)、粒子滤波算法(particle filter，PF)。EKF算法具有实时数据处理能力，在非线性强度较弱的动态数据处理时有较大的优势；但是对于强非线性系统，线性化的EKF方法会出现较大的截断误差，甚至导致滤波发散，算法的定位精度严重降低。粒子滤波器(PF)在非线性情况下有较好的性能，但是需要大量的粒子样本才能达到最优的滤波效果[3]。UKF滤波算法是用固定量的参数去近似一个高斯分布，比近似任意的非线性函数或变换更容易；UKF算法的滤波效果不会受到非线性强度的影响，更加适用于AUV导航系统中非线性的动态估计。

在实际的观测过程中，观测数据难免存在观测粗差。UKF算法无法随着观测系统的改变而进行自动调节，影响了实时滤波估计结果，从而大大减少了UKF滤波算法的稳定性和滤波解的精度。为了抑制观测粗差对滤波结果的影响，提高滤波结果的稳定性，文献[4]分别提出了多模型自适应估计法(multiple model adaptive estimation，MMAE)、采用预报残差向量估计当前观测残差的协方差矩阵的自适应开窗估计法(innovation-based adaptive estimation，IAE)、采用测量残差向量估计当前观测残差的协方差矩阵的自适应开窗估计法(residual-based adaptive estimation，RAE)。MMAE算法要求几种平行的卡尔曼滤波器进行估计从而获得滤波的正确统计信息，导致了估计效率降低，IAE法和RAE法对观测噪声协方差矩阵进行估计，要求各历元观测信息不仅同类、同分布，而且同维。文献[5-6]基于残差向量，采用观测信息的等价协方差矩阵原理，给出了基于M估计的抗差UKF的算法。文献[7]提出了一种测量噪声比例因子，将其与观测噪声协方差矩阵相乘以减弱观测粗差的影响。

本文结合2段函数模型和测量噪声比例因子构造抗差因子函数，进而计算UKF算法中的增益矩阵，同时利用文献[8]提出的统计信息来进行粗差探测，以期改善仅依据残差进行粗差探测而无法完全正确识别粗差的问题。

1 基于长基线的AUV水下声学导航系统

目前大部分的AUV都装有全球卫星导航系统(global navigation satellite system，GNSS)接收机，用来对水面航行时的AUV定位校准，且方便回收。为解决水下导航的问题，则要结合水下定位系统和惯性导航系统得到AUV的位置信息和航向信息。基于长基线的AUV导航的基本原理如图1所示。

图1 基于长基线的走航式水下定位

从图中可知，走航式布设海底应答器的工作过程类似于空间全球定位系统(global positioning system，GPS)的原理[9]。搭载着GPS接收机的测量船可以得到船的实时位置，并利用姿态仪测量船体的实时姿态。船的实时位置和姿态数据可换算出船底换能器的实时位置。换能器通过发射声脉冲信号并接收水下应答器的应答信号，得到换能器与应答器之间的双向距离。测量船沿某一航迹航行可以得到不同时刻的多组观测值，再进行后处理就可以解算出应答器在WGS-84坐标系统中的坐标[10]。

通过走航式布设海底应答器同时进行应答器位置的求解，可以求得海底应答器的位置，原理如图2所示。

图2 AUV水下声学定位原理

已知海底应答器的空间三维坐标位置为x，海底AUV的三维坐标位置为xk，k时刻测得的AUV至应答器的距离zk(传播时间乘以声速)，则有AUV导航的观测方程和状态方程为

观测方程：zk=h((xk,x),vk)

(1)

状态方程：xk=f(xk-1,wk-1)

(2)

式中：坐标系为局部地方坐标系，坐标原点可设为研究区域的任意合适位置，坐标轴可设为北、东、天或者自定义的空间直角坐标系：h(·)为关联k时刻状态xk和k时刻测量向量zk的更新方程；f(·)为关联k-1时刻状态xk-1和k时刻状态xk的差分形式的预测方程；wk-1为过程噪声向量；vk为观测噪声向量。

2 AUV动态导航中的UKF滤波

2.1 基于M估计的抗差UKF滤波

UKF的基本原理是在原先状态分布中按某一规则(U变换)取一些点，使这些点的均值和协方差等于原状态分布的均值和协方差，将这些点代入非线性函数中，相应得到非线性函数值点集，通过这些点求取变换后的均值和协方差[6]。UKF滤波算法的步骤如下：

1)初始化

(3)

(4)

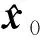
2)时间更新

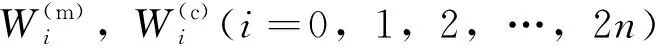
(5)

(6)

(7)

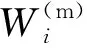
计算预测σ点，即

(8)

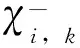
计算预测估计值和预测协方差，即

(9)

(10)

式中Qk表示状态噪声协方差矩阵。

3)计算预测量测值，即

(11)

式中h[]表示量测方程函数。

4)计算信息方差和协方差，即

(12)

(13)

式中Rk表示量测噪声协方差矩阵。

5)计算Kalman增益，即

(14)

6)更新状态和协方差，即

(15)

(16)

基于M估计的抗差UKF的滤波方程只需在标准UKF滤波方程的基础上，利用稳健M估计等价权原理[11]求逆计算等价协方差阵，对噪声协方差阵Rk进行等价协方差的替换，从而起到调节Kalman滤波增益的作用，以使滤波方程对导航系统中存在的观测粗差有较强的抵抗作用，进而消除滤波方程发散的可能性[6]。

根据标准UKF方程，建立基于M估计的抗差UKF的滤波模型，只需对式(12)进行修改为

(17)

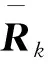
稳健M估计目前常用的方法有Huber法[12]、IGGⅢ法等，本文将应用IGGⅢ法计算等加权，求逆获得等价协方差矩阵，减小或消除粗差对估计结构的影响。等价权的计算公式[13]为

(18)

(19)

(20)

2.2 改进的抗差UKF滤波

当观测值不含有粗差时，标准的UKF算法可以得到较好的滤波结果；一旦观测值中含有粗差，必定会影响状态参数的估计，得不到可靠的滤波结果，甚至导致滤波发散。由式(21)可以看出粗差通过状态增益矩阵K影响到状态滤波值；由式(22)可知，通过采用基于预报残差的测量噪声比例因子Sk来调节信息方差；同时由式(23)求得正确的滤波增益值，最终得到准确的状态滤波结果。其计算过程为

(21)

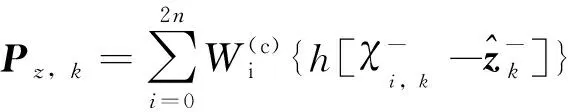
(22)

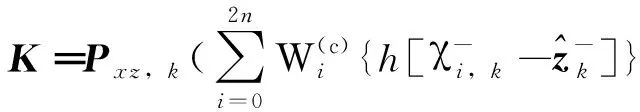
(23)

改进的抗差UKF算法的核心是测量噪声比例因子Sk的确定。式(24)中，不等式左侧是真实的信息方差值，不等式右侧是预报信息方差值。当量测值不等于预测量测值时，真实的信息方差值就会超过预报信息方差值，因此需要测量尺度因子Sk来调节信息方差。

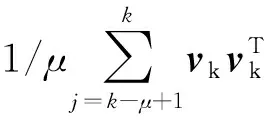
(24)

为了计算测量噪声比例因子Sk，由式(24)构造式(25)，考虑式(26)的情况，得到测量噪声比例因子Sk即式(27)[8]。

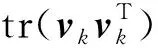
(25)

(26)

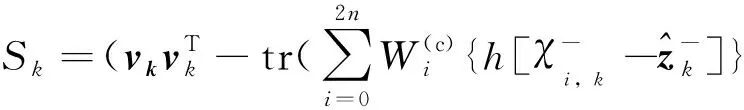
(27)

(28)

(29)

式中：

这个值来自χ2分布时的自由度是9，可靠性水平是95 %。

在标准UKF的基础上，由式(29)计算得到的滤波增益矩阵根据式(15)更新状态和协方差，从而得到正确的滤波结果。

3 实验及结果分析

模拟海上AUV的定位方式如图3所示。模拟海底应答器阵对AUV进行导航，用三角符号表示应答器，4个应答器呈中心放射状布设在海底，应答器的坐标分别为(0 m，500 m，-497 m)，(435 m，-253 m，-486 m)，(-428 m，-232 m，-474 m)，(5 m，7 m，-456 m)。模拟AUV在水下100 m深的位置做匀速转弯运动，AUV的运动参数分别是X坐标、Y坐标、速度、半径和转向角，AUV的初始位置是(100 m，0 m，-100 m)，半径为100 m，转向角为π/100，仿真100个历元，采样间隔1 s，采用Munk声速剖面和射线跟踪算法模拟观测量，并对观测量添加随机噪声，同时每隔几个历元对其量测值分别添加10～15 m的随机观测粗差，然后将滤波结果分别与已知的坐标值作差，改变AUV的初始位置，模拟20个历元，每个历元都是加入的随机粗差；算法中采用最小二乘估计初始值，重复上述过程。

文章通过仿真算例对标准UKF、粒子滤波、改进的抗差UKF与基于M估计的抗差UKF进行对比分析，结果如图4～图5、表1所示。

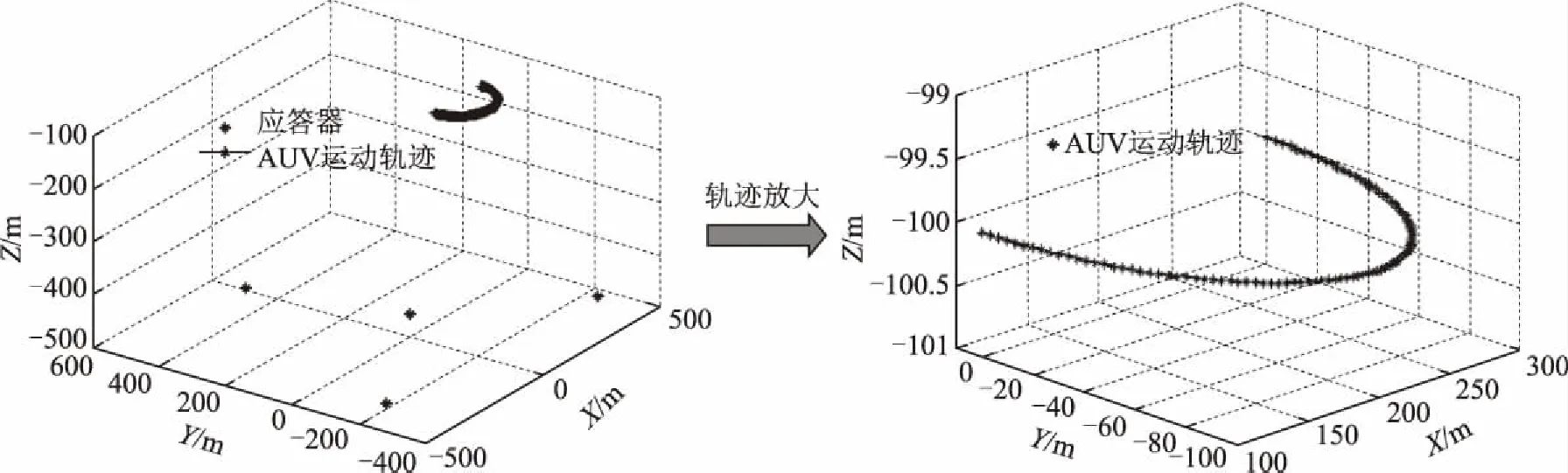
图3 海上AUV曲线运动轨迹和海底应答器模拟示意

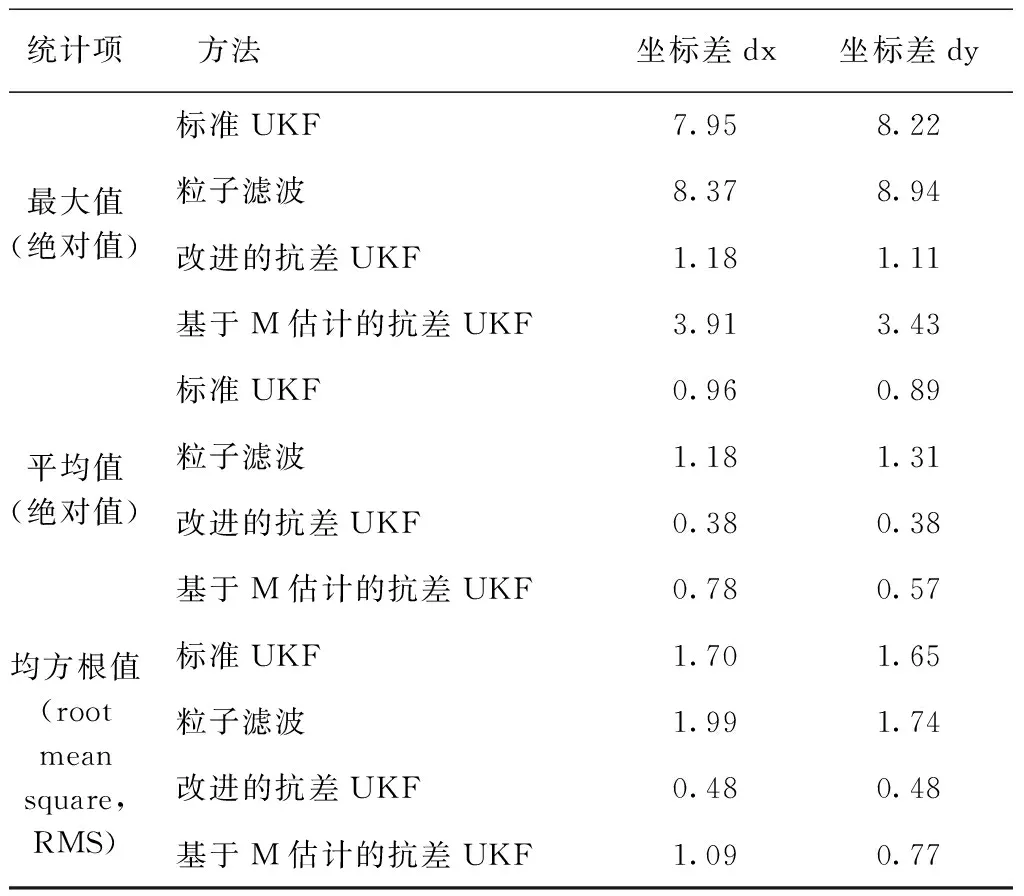
表1 含粗差时4种滤波算法的X、Y坐标差值统计 m

为了验证算法的精度和稳定性，改变AUV的初始位置，利用标准UKF、粒子滤波、改进的抗差UKF与基于M估计的抗差UKF进行解算，得到结果如表2所示。图6为改进的抗差UKF与基于M估计的抗差UKF算法的精度比较结果。

结果分析如下：

1)由图4可以看出：在观测无粗差时，2种抗差UKF算法和标准UKF算法得到的滤波结果相当；但是由于观测值中加入了随机噪声，基于M估计的抗差UKF仅仅基于预报残差来进行粗差探测，导致滤波结果在某一历元采样时刻出现较小的偏差；粒子滤波算法的定位精度与标准UKF算法的效果相当。

2)由图5可以看出：在观测值中存在粗差时，标准UKF算法和粒子滤波算法不能对数据中的粗差进行处理，由于粒子权重错误选取导致定位结果出现错误[15]，标准UKF滤波由于不具有抗差性，所以滤波估值存在较大的误差；2种抗差UKF算法都可以判断出含粗差的观测值，并且不同程度上抑制粗差观测值对滤波结果的干扰。从表1可知，本文中改进的抗差UKF算法的最大值、平均值和RMS值都要小于基于M估计的抗差UKF算法，当粗差影响较大时，可以得到更为可靠的滤波结果。

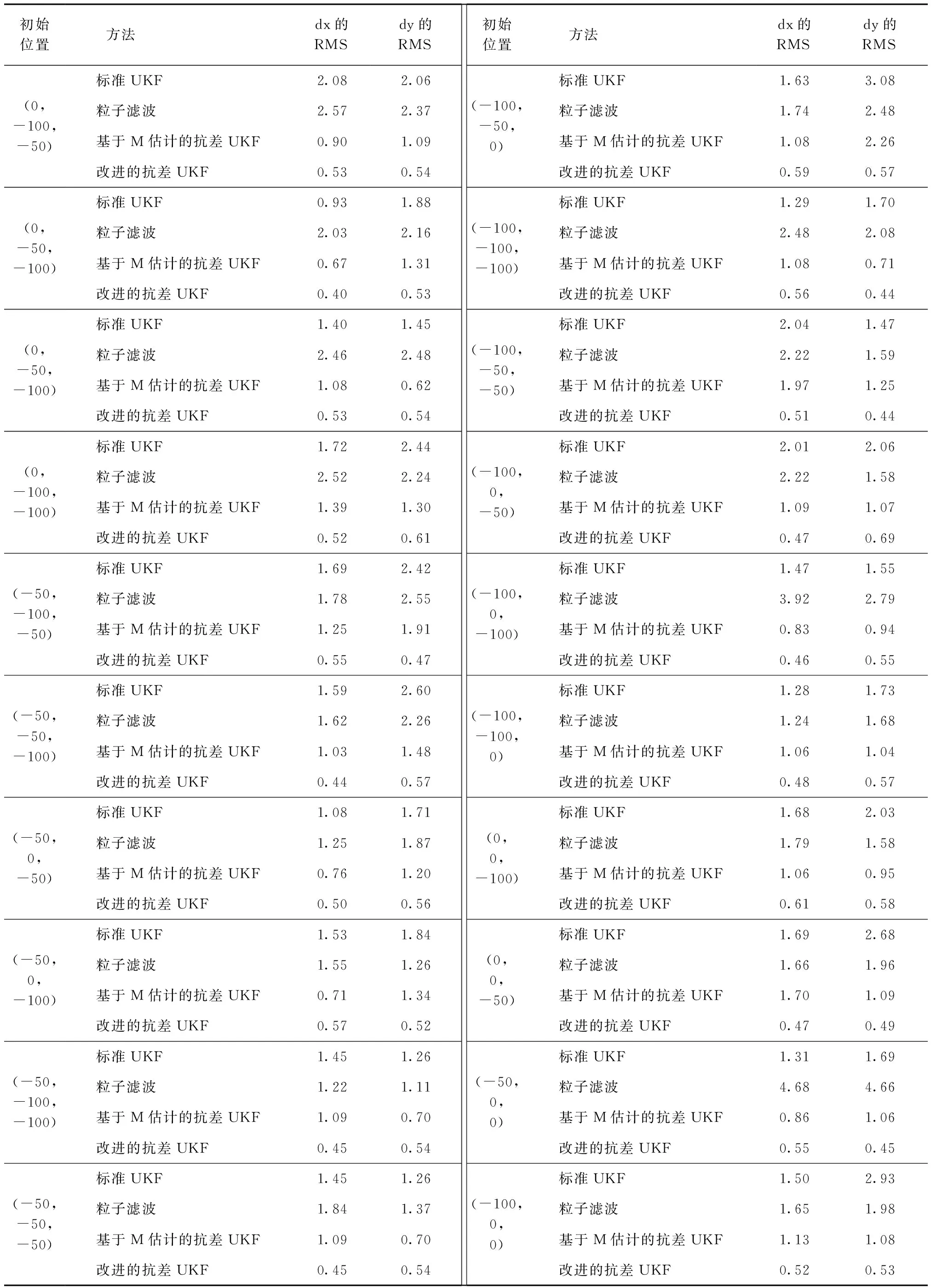
表2 含粗差初始位置不同时4种滤波算法坐标差值的RMS值统计 m

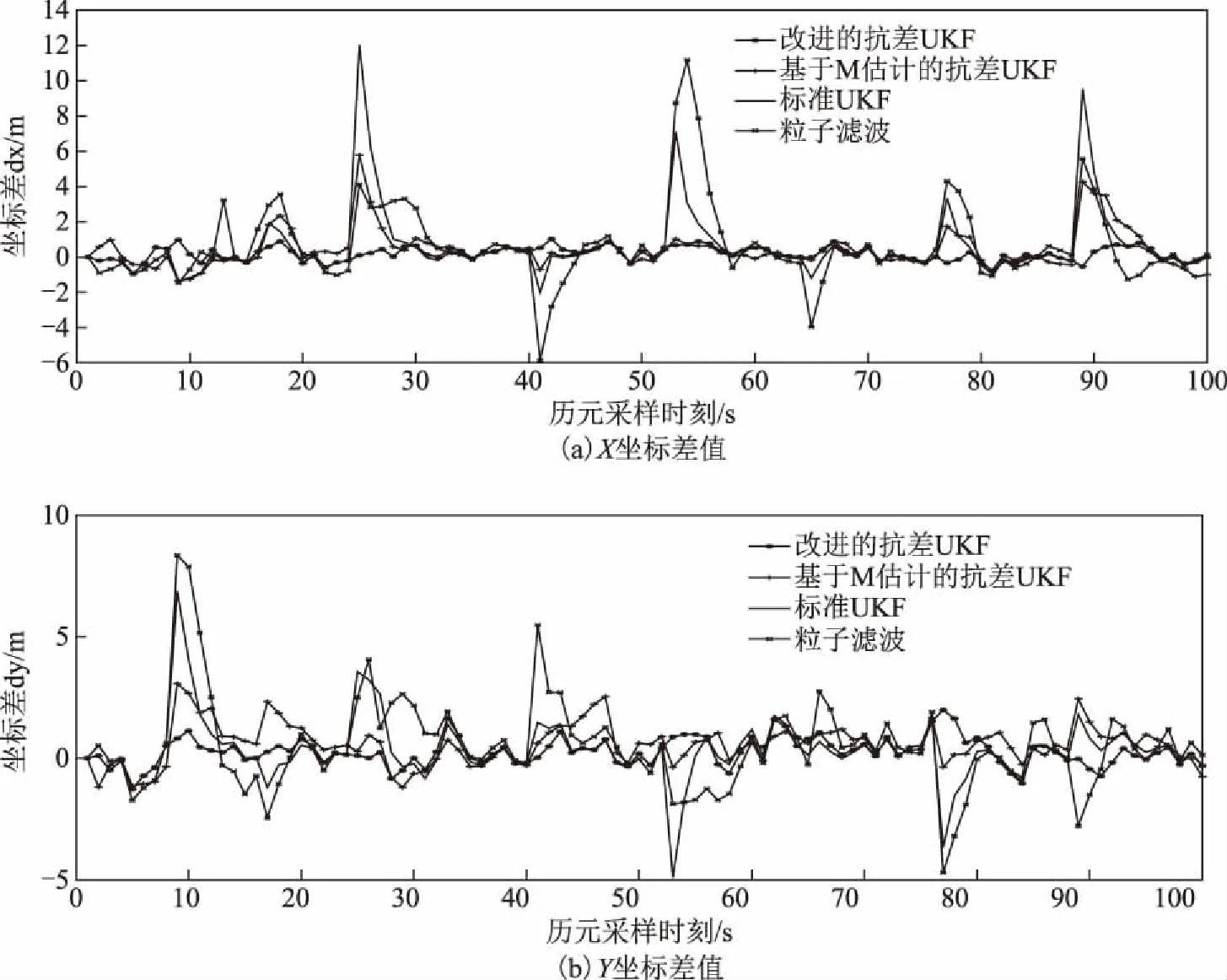
图5 含粗差时4种滤波算法解算结果对比

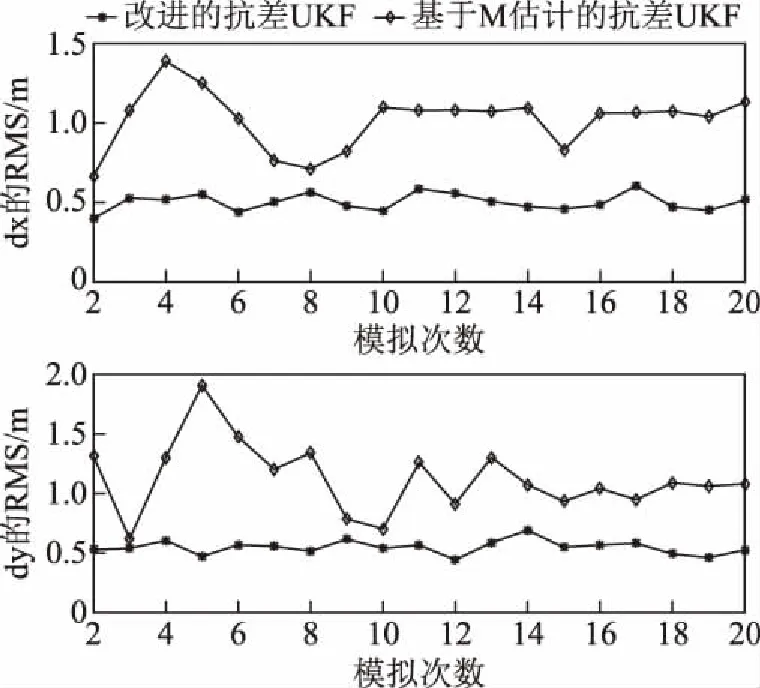
图6 模拟20次的2种抗差UKF算法的RMS值对比

3)为了验证算法的有效性和稳定性，模拟20个历元对2种抗差算法进行对比分析。由表2可以看出：标准UKF和粒子滤波不具有抗差性，定位精度较差且结果相当；另2种抗差滤波定位精度明显提高。由图6可以看出，本文中改进的抗差UKF算法不仅具有较高精度的滤波结果，而且与基于M估计的抗差UKF算法相比，改进的抗差UKF具有更好的稳定性。

4 结束语

1)预报残差可以判断观测值是否存在粗差；但是由于1个粗差影响所有残差，使得仅利用预报残差进行粗差探测会出现偏差。本文基于预报残差和信息方差来进行粗差探测，可以更为准确地判断观测值是否存在粗差：结合2段函数和测量尺度因子来构造抗差因子，利用抗差因子增大观测协方差来减小存在观测粗差的滤波增益，可以降低观测粗差对滤波估值的影响，提高滤波解的精度和可靠性。

2)由于采用2段函数模型来构造抗差因子，使得滤波算法仅受1个常数的影响，可以提高算法的稳定性，使其在实际观测数据的粗差处理上更具优势。

[1] CHANDRASEKHAR V, SEAH W K, CHOO Y S, et al. Localization in underwater sensor networks-survey and challenges[EB/OL].[2017-07-16].http://vijaychan.github.io/Publications/2006%20-%20Localization%20in%20Underwater%20Sensor%20Networks-%20Survey%20and%20challenges.pdf.

[2] 崔海英,崔鑫山,罗康,等.粒子滤波在AUV组合导航技术上的应用研究[J].声学技术, 2014,33(5):269-270.

[3] LEFEBVRE T, BRUYNINCKX H, SCHUTTER J D. Kalman filters for nonlinear systems[EB/OL].[2017-07-16].https://link.springer.com/chapter/10.1007%2F11533054_4.

[4] HIDE C, MOORE T, SMITH M. Adaptive Kalman filtering algorithms for integrating GPS and low cost INS [EB/OL].[2017-07-16].https://ieeexplore.ieee.org/document/1308998/.

[5] 李雪鹏,张幼群,包括. UKF的改进算法及其在伪卫星定位中的应用[J]. 测绘科学技术学报, 2008, 25(2):108-111.

[6] 汪秋婷.自适应抗差UKF在卫星组合导航中的理论与应用研究[D].武汉:华中科技大学,2010.

[7] HAJIYEV C. Adaptive filtration algorithm with the filter gain correction applied to integrated INS/radar altimeter[J]. Journal of Aerospace Engineering, 2007, 221(5):847-855.

[8] HAJIYEV C, ATA M, DINC M, et al. Fault tolerant estimation of autonomous underwater vehicle dynamics via robust UKF[EB/OL].[2017-07-16].https://innovate.ieee.org/see-if-your-organization-or-institution-qualifies-for-a-free-trial-of-ieee-xplore/?LT=XPLLG_XPL_Bold728x90_2018_FT_Subpage.

[9] 李莉.长基线阵测阵校阵技术研究[D].哈尔滨：哈尔滨工程大学，2007.

[10] SATO M，FUJITA M，MATSUMOTO Y，et al.Improvement of GPS acoustic seafloor positioning precision through controlling the ship’s track line[J].Journal of Geodesy，2013，87(9)：825-842.

[11] 张凯，赵建虎，张红梅.一种基于M估计的水下地形抗差匹配算法[J].武汉大学学报(信息科学版)，2015，40(4)：558-562.

[12] 赵全哲，徐爱功，徐宗秋，等.基于稳健总体最小二乘的GPS水准拟合[J].导航定位学报，2017，5(1)：95-99.

[13] 杨元喜.等价权原理：参数平差模型的抗差最小二乘解[J].测绘通报.1996(6)：33-35.

[14] 杨元喜，任夏，许艳.自适应抗差滤波理论及应用的主要进展[J].导航定位学报，2013，1(1)：10-15.

[15] 范澎湃，隋立芬，曹轶之.观测值含有粗差的抗差粒子滤波算法[J].测绘工程，2009，18(2)：24-27.