数字信号处理案例教学法研究与实践

2018-06-05张晓光汤文豪王艳芬

实验技术与管理 2018年5期

张晓光, 汤文豪,2, 王艳芬, 王刚

(1. 中国矿业大学信息与控制工程学院, 江苏徐州 221116；2. 天津大学电气自动化与信息工程学院, 天津 300072)

“数字信号处理”课程概念抽象、理论繁琐,学生面对各种繁杂的公式和算法推导,很容易丧失学习兴趣,难以从应用的角度去掌握和理解[1-3]。传统教学以教师为主,难以发挥学生学习的主动性,但采用案例式教学方法能有效解决这个问题。结合案例式教学方法,精心设计与教学内容结合紧密的实验案例,理论课上引入案例、实验课上进行设计实践、开放实验室内课外兴趣小组进行拓展创新实践[3-5]。整个过程以学生为主、教师为辅,通过实训,学生能够将课堂内容与实践应用结合起来,增加学生对于课程内容的参与、体验以及分享,使学生的知识获取从枯燥、呆板的被动学习模式,变为趣味、生动的主动学习模式[6-7],激发学生学习兴趣和创新能力。

1 案例教学设计

合理的案例设计是保证教学效果的关键,案例既要涵盖数字信号处理的主要理论知识,又要和实践应用相结合。同时,案例要按照理论知识讲解的进度进行合理分解,保证学生在做任务过程中学习理解相应的理论知识[4-5,7]。数字信号处理课程是一门重要的专业基础课,主要学习离散时间信号及系统、离散傅里叶变换(DFT,及其快速算法FFT)、数字滤波器的设计等内容。将美妙的音乐、有趣的图像等引入课堂会引起学生的共鸣,容易激发学生学习的兴趣,为此,整个教学过程围绕图1所示“玛丽莲•爱因斯坦”的图像合成展开。

图1 玛丽莲·爱因斯坦

“玛丽莲·爱因斯坦”的趣味性在于它的变化性:远看它是玛丽莲·梦露,近看是爱因斯坦；放大看是爱因斯坦,缩小看是玛丽莲梦露。为了合成图1,首先要将图2对应的2幅原始图像(分辨率均为225×265)提供给学生,然后根据教学内容将整个项目分解为3个子任务:图像信号的频谱分析、图像信号的滤波以及图像信号的合成。

图2 两幅原始图像

1.1 图像信号频谱分析

频谱分析这一步需要学生在理解一维离散傅里叶变换理论基础上,学习图像信号二维离散傅里叶变换原理及其实现过程,掌握图像和其傅立叶变换系数之间的关系[8]。该部分布置给学生的子任务有2个。

1.1.1 图像频谱理论分析

二维DFT变换对为

(1)

(2)

式中x,u=0,1,…,M-1；y,v=0,1,…,N-1。

设f(x,y)是一幅M×N的图像,其频谱示意如图3所示。图像的二维频谱对应着图像像素值在2个相互垂直方向上的变化程度,频谱图中沿u、v方向在u,v=0,N/2,N-1三点处的频率分别为f0=0,fN/2=fmax=fs/2(fmax为信号的最高截止频率,fs为采样频率),fN-1=0。因而,频谱图的4个角(0,0)、(0,M-1)、(N-1,0)和(N-1,M-1)处沿和方向的频率分量为0,频谱图中心(N/2,M/2)处沿和方向的频率分量为最大值fmax。由于图像中能量主要集中在低频分量上,即频谱图4个角区域能量较大,但4个角范围较小且不集中,实际中不利于图像分析,因此利用周期性和共轭对称性对频谱图坐标移位,使高频成分于四周,所有低频成分集中于频谱图中心,对图3进行频谱移位后,相当于A、D对调,B、C对调。

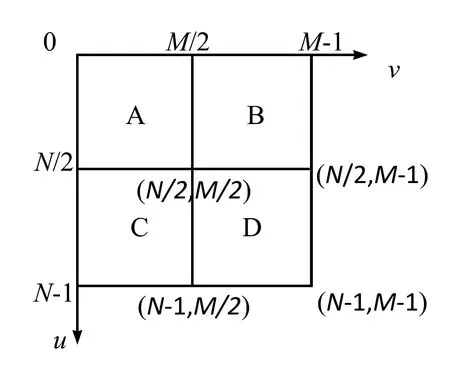
图3 频谱示意图

1.1.2 图2所示两幅原始图像的FFT频谱分析

仿真实验在Matlab2014a、Windows7下进行。图4所示为图2两幅原始图像经离散傅里叶变换后呈现的频谱图像。频谱图中间部分为低频分量,越向外部扩展频率越高,从图4可以看到此时图像中的大部分能量集中在低频区,高频区能量很少。

图4 两幅原始图像的频谱

1.2 图像信号的滤波

图1所示图像之所以能在不同状态毫不违和地呈现2种不同画面,有2个原因:一是图像信号处理技术,简而言之就是图2(a)通过合适的低通滤波,图2(b)通过合适的高通滤波,然后两者有效地合成在一起；二是人眼具有视觉感知特性,在近距离观察图像时对高频细节十分敏感,看到的是高通滤波后的图像；在远距离观察图像时高频信息逐渐消失,低频信息被人眼感知到,看到的则是低通滤波后的图像。因此如何根据案例中图像的要求确定滤波器的参数,设计满足要求的滤波器是本任务的主要目标。该部分布置给学生的子任务有2个。

1.2.1 图像信号的FIR滤波方式

数字信号处理课程主要讲授了IIR和FIR两类滤波器的设计方法,IIR数字滤波器设计简单、阶数低,但相位非线性会引起频率的色散,不利于图像信号的处理,而FIR数字滤波器具有严格的线性相位,因此为了实现本任务,在IIR和FIR滤波器中只能选择FIR滤波器[9]。

二维FIR滤波器在时域上可以用有限长单位脉冲响应表示为

h(n1,n2)=w(n1,n2)hd(n1,n2)

(3)

式中w(n1,n2)是二维的窗函数,hd(n1,n2)是理想滤波器的无限长单位脉冲响应。时域相乘,对应的频域为卷积关系,因此二维FIR滤波器的频谱为

H(ω1,ω2)=

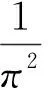
(4)

下面是应用Matlab软件,选择海明窗设计的线性相位二维FIR低通滤波器的程序代码。

%线性相位二维FIR低通滤波器:

[f1,f2]=freqspace(51,′meshgrid′);

hd=ones(51);

r=sqrt(f1.^2+f2.^2);

hd((r>0.15))=0; %%低通

mesh(f1,f2, hd)

h=fwind1(hd,hamming(51));

freqz2(h);

title(′基于hamming窗的低通幅度′)

图5所示为线性相位二维FIR低通滤波器的三维立体仿真波形。同样,可以得到线性相位二维FIR高通滤波器的三维立体仿真波形如图6所示。

1.2.2 图2所示2幅原始图像的滤波处理

利用线性相位二维FIR滤波器,分别实现图2(a)的高通滤波和图2(b)的低通滤波。图7是原始图像经过滤波处理后得到的图像,从(a)图可以看到“爱因斯坦”经高通滤波后只留下边缘细节,从(b)图可以看到“玛丽莲”经低通滤波后滤除了边缘细节，因而图像变得模糊。

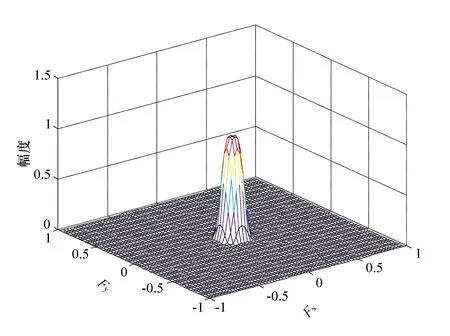
图5 低通滤波器

图6 高通滤波器

图7 原始图像经过滤波处理

1.3 课外拓展

课外拓展以小组为单位,要求学生在完成基本实验之后有更深入的思考,鼓励学生充分发挥创造力。图像合成子任务不是“数字信号处理”教学的重点内容,但能够引导并鼓励学生将基本实验成果与实际应用结合在一起。

1.3.1 图像信号的合成

在频域中,假设I1表示图2(a)图,I2表示图2(b)图,G1表示图5所示的线性相位FIR低通滤波器,1-G2表示图6所示的线性相位FIR高通滤波器,则合成图像H可表示为

H=I1·G1+I2·(1-G2)

(5)

为了显示图像合成的效果,本文将合成图像缩放成不同的尺寸,并将它们拼接成一张图,如图8所示。从图8中可以看到随着图像尺寸的变小,图像内容由爱因斯坦变为玛丽莲梦露。

图8 图像合成效果

1.3.2 影响该图像合成效果的2个因素

在图像合成时,滤波器参数的合理选择是至关重要的,不仅与图像尺寸有关,还与图像内容密切相关[10-11]。

(1) 滤波器截止频率差距的影响。由图9和图10可以看出,当FIR低通和FIR高通滤波器恰好互补的时候,混叠效果不理想；而当两个滤波器的截止频率(幅度下降到0.5时对应的频率)呈现一定的差距的时候,混叠效果才比较好。

(2)频率通道的影响。频率通道的选择也是影响合成效果的重要因素。如图11所示,如果将 “爱因斯坦”与“玛丽莲”相互交换频率通道,即原来高通的图像现在低通,原来低通的图像现在高通,效果会大打折扣。

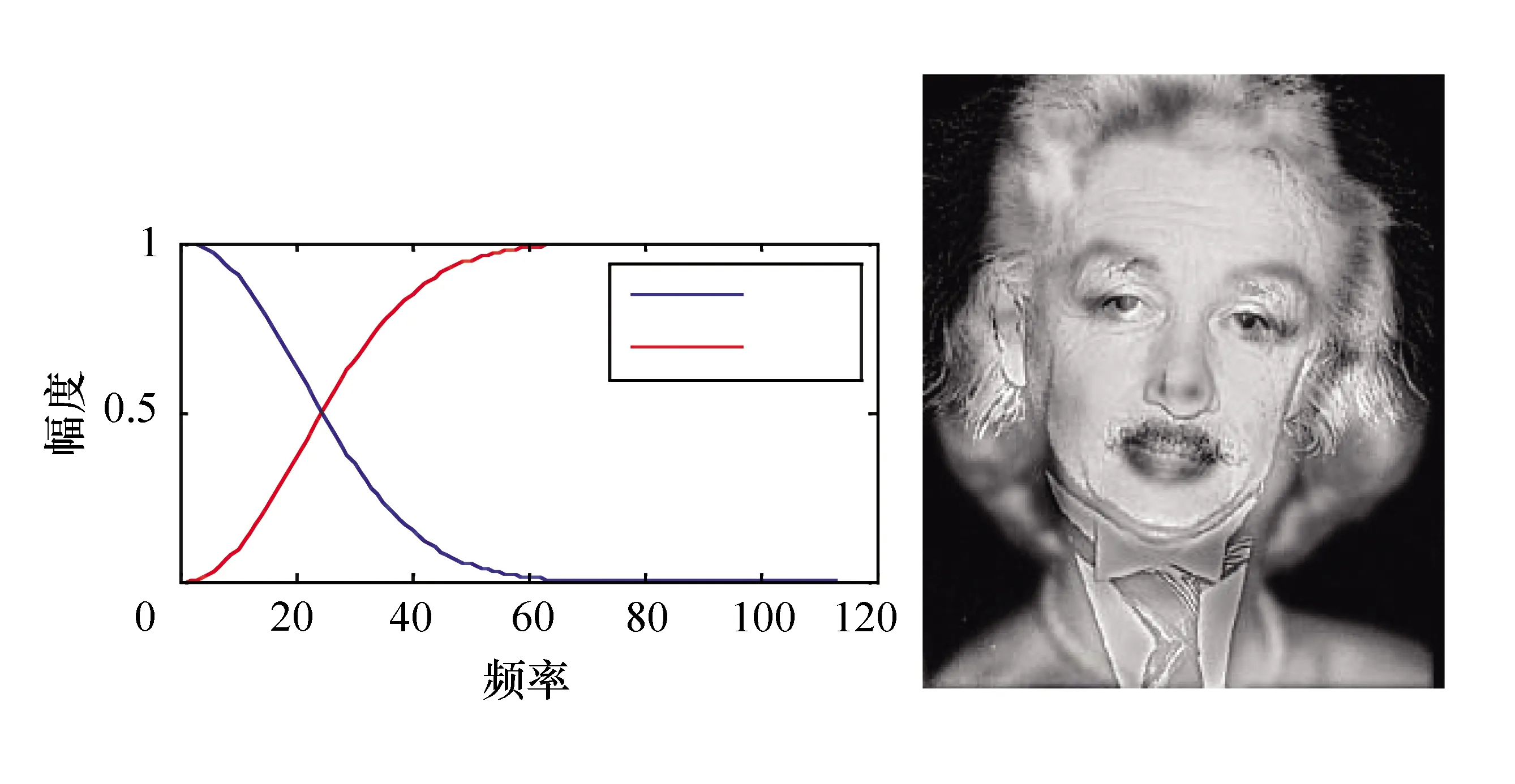
图9 Gap较小时—合成图像效果

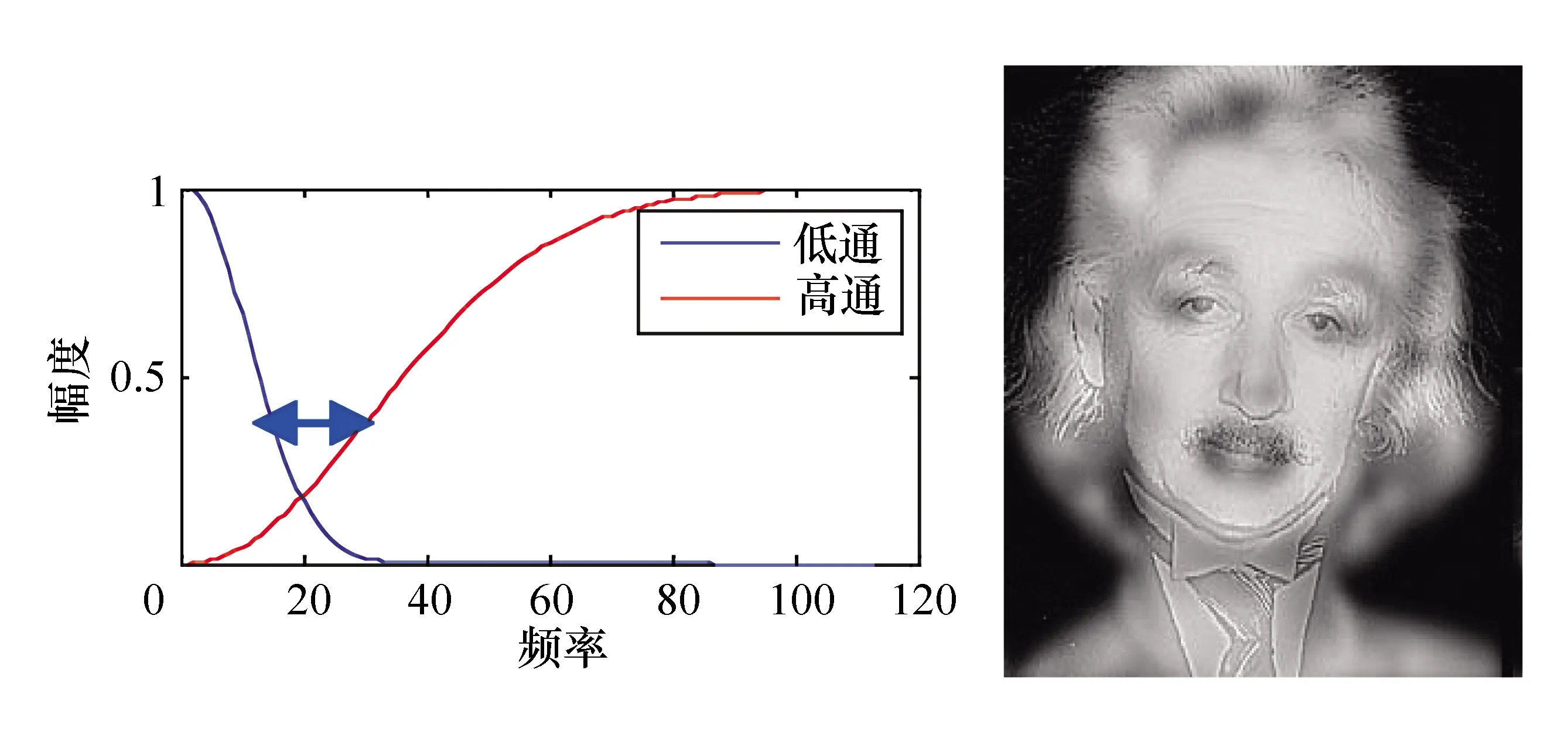
图10 Gap较大时—合成图像效果

图11 交换频率通道后的合成图像效果

本案例中涉及的图像是灰度图像,而彩色图像包含的信息量更大,在相同模糊程度下,颜色更容易被人眼察觉,因此课外拓展中也会鼓励有兴趣的学习小组对彩色图像进行合成设计与效果探讨。

2 教学组织

“数字信号处理”绪论课上,任课教师将“玛丽莲•爱因斯坦”引入课堂,演示整个图像信号的处理过程,让学生看到不同处理后的图像效果,激发学生的求知欲望。然后对应演示步骤,介绍每种处理用到的知识点,结合理论教学单元将案例进行同步分解,用案例子任务将整个教学内容贯穿起来；当子任务对应的理论教学结束之后,教师督促学生以小组形式开展案例的实验设计工作。实验课上,在前2个基本子任务完成后,要求优秀作品小组学生代表做交流总结,拓展子任务部分,仍以小组为单位,引导并鼓励学生将基本实验成果与实际应用结合在一起。整个任务完成后,由任课教师验收,每个小组需要提交一份案例实践报告,并将成果制作成PPT展示及接受教师提问,最终根据学生回答问题的情况和实践报告综合打分,所得成绩占整个数字信号处理结业考试的10%。