新工科教育中离散数学教学改革探讨

唐新亭, 张小峰, 杨洪勇

(鲁东大学 信息与电气工程学院, 山东 烟台 264025)

新工科是“卓越工程师教育培养计划”的升级版,要面向产业界、面向世界、面向未来,深化工程教育改革、加快建设新工科,促进我国工程教育加速进入世界第一方阵。从理念引领、结构优化、模式创新、质量保障、分类发展5个方面持续深化工程教育改革。在离散数学的授课与学习过程中存在明显的误区,认为构成计算机科学的核心是数据结构、算法和程序设计,忽略了离散数学在思维培养和实践能力训练中的重要性,片面强调离散数学的理论性。在一些高校进行培养方案的设计与调整时,也明显存在压缩离散数学课时的问题。离散数学不仅对于思维培养有很大作用,而且对于应用实践能力培养也有非常关键的作用。

1 目前离散数学授课中存在的问题

和其他工程数学一样,离散数学的内容常常因书而异、因学校而异。经过多年的实践,对于离散数学的授课内容有了统一的认识。左孝凌老师指出,离散数学的授课内容包括5部分:数理逻辑、集合论、代数系统与布尔代数、图论、形式语言与自动机[1]。然而,随着计算机科学的快速发展,许多高校在设计离散数学的教学内容时,对上述内容有所取舍,并结合不同高校的专业发展特色,增加了新的内容。例如,北京大学屈婉玲教授为主的离散数学教学团队,对代数系统内容进行压缩,增加了组合数学的知识,对基本的计数原则、递推式进行了介绍；河北地质大学对离散数学的授课内容进行改革,将离散数学分为3个学期上课,分别介绍数理逻辑与集合论、图论和代数系统。

在课时的设计上,大部分高校安排的课时是72左右,但部分地方高校为了突出应用型人才培养,对离散数学的课时进行挤压,有部分高校离散数学的课时甚至被压缩到了32课时,这给离散数学的教学工作带来了很大的困难。

在教学模式上,由于离散数学的特点,许多教师采取了以教师为主、满堂灌的传统教学模式,导致了学生在学习离散数学时,感受的只是课程的枯燥、乏味,甚至导致学生失去了学习后续专业课程的动力与兴趣,这对专业学习非常不利。

2 面向新工科教育和应用实践能力进行改革

我校是山东省内一所普通的二本院校,具有明显的师范高校特色,2007年更名后,开始朝着综合型、应用型大学转型发展。

2.1 学习兴趣的培养

一般而言,数学类的课程比较枯燥,如何提高学生在学习离散数学时的学习兴趣,是一门学问,更是一门教学艺术。在授课过程中,借助离散数学发展史和相关学科发展的前沿知识提高学生的学习兴趣,可收到较好的效果[2]。

(1) 在数理逻辑部分,介绍德摩根(Augustus de Morgan,1806—1871)对符号化推理演算的贡献,介绍德摩根与阿达(Augusta Ada King,1815—1852,英国著名诗人拜伦的女儿)的师生关系。在消解律部分,围绕人工智能学科的产生、发展,介绍人工智能的发展历程,从最初的感知机,引进到神经网络,直至最新的深度计算,让学生对学科最前沿的知识有所了解。

(2) 在布尔代数部分,介绍数学史上的两个天才人物伽略瓦(Évariste Galois,1811—1832)和阿贝尔(Niels Henrik Abel,1802-1829),让学生在敬仰他们取得的数学成就的同时,对数学产生兴趣。

(3) 在集合论部分,介绍德国数学家康托尔(Georg Ferdinand Ludwig Philipp Cantor,1845—1918)以及冯·诺伊曼(John von Neumann,1903—1957)对集合论的贡献,介绍罗素(Bertrand Russell,1872-1970)在集合论的公理化上的贡献。在德摩根律部分,介绍布尔(George Boole,1815—1864)对德摩根律的贡献,同时对问题进行进一步扩展,介绍香农(Claude Elwood Shannon,1916—2001)利用开关电路实现布尔代数,同时介绍图灵(Alan Mathison Turing,1912—1954)设计的计算模型,为电子计算机的最终实现奠定了必要的基础。

(4) 在图论部分,介绍伟大数学家欧拉(Leonhard Euler,1707—1783)的传奇人生,同时也介绍对推动四色定理证明而努力奋斗的德摩根、哈密尔顿(William Rowan Hamilton,1805—1865)、凯莱(Arthur Cayley,1821—1895)、肯普(Alfred Kempe,1849—1922)、海伍德(Percy John Heawood,1861—1955)等系列数学家。在树部分,围绕哈夫曼树,介绍费诺(Robert Fano,1917—2016)与哈夫曼(David A. Huffman,1925—1999)在数据压缩、编码等领域的贡献。

通过介绍离散数学的发展史和计算机的学科前沿知识,可以让学生了解相关知识点的由来、发展,同时了解相关学者为了问题的解决而奋斗的经历,这对提高学生的学习兴趣、培养学生的创新意识非常有益。

2.2 思维训练

离散数学不仅是数据结构、算法分析与设计等后续专业课程的基础,而且在计算机相关专业的人才培养过程中对思维的训练起着非常关键的作用,授课教师在教学过程中应该注重并强化这一点[3-5]。以德摩根律的证明来说明如何在教学过程中对学生的思维进行训练。

德摩根律是描述集合运算间的关系,可以表述为:

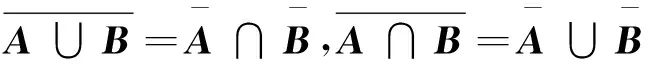
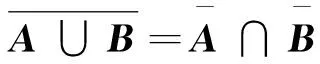
在证明这2个子问题时,需要根据集合运算的性质,将一个集合从一种表现形式转换为另一种形式。

如果授课过程中按照上述思路对问题进行分析,可以消除学生对于离散数学的恐惧心理,对后续专业课程的学习,很有帮助。

2.3 应用实践能力培养

计算机等相关专业的一个特点是对应用实践能力要求较高,所有的课程都应为培养学生的应用实践能力服务。在离散数学的授课过程中,将提高学生的程序设计能力作为教学的落脚点,通过设计教学案例,将离散数学的学习与学生程序设计能力的提高结合起来,既提高了学生的学习兴趣,又让学生体会到了离散数学对后续专业课程的重要性。通过几个简单的例子加以说明。

(1) 张三说李四在说谎,李四说王五在说谎,王五说张三李四都在说谎[6]。这是命题逻辑中的一个非常经典的问题,一般结合主析取范式进行求解,并结合“等价”这个联结词的特性进行分析。在授课过程中,对该问题的求解分为3个不同的层次:(a)让学生自行分析,培养他们思考和解决问题的方法；(b)通过主析取范式,将命题逻辑与后续课程数字电路的逻辑代数打通,方便学生推导；(c)通过编程实现,进一步提高学生的编程能力,可以将上述问题设计为如下的程序:

#include

int main()

{

int a,b,c;

for(a=0;a<=1;a++){

for(b=0;b<=1;b++){

for(c=0;c<=1;c++){

if(((a&&!b)||(!a&& b))&&((!b&&c)||(b&&!c))&&((c&&a+b!=0)||(!c&& a+b==0))){

printf(″张三%s说谎 ″,a?″在″:″没有″);

printf(″李四%s说谎 ″,b?″在″:″没有″);

printf(″王五%s说谎 ″,c?″在″:″没有″);

}

}

}

}

return 0;

}

(2) 关系的复合运算满足结合律。关系复合运算的这一性质属于纯数学范畴,学生在学习过程中由于不知道结合律的应用,因而普遍比较头疼。在授课过程中,将复合运算的结合律与矩阵的连乘结合起来。由于关系的复合可以用矩阵的乘法进行表示,因而,关系的复合运算满足结合律等价于矩阵的乘法运算满足复合律。进一步,利用矩阵乘法运算的复合律,可以计算矩阵乘法运算的最优次序[7-8]。例如,对于3个矩阵来说,设矩阵A1的维数是5×10,矩阵A2的维数是10×100,矩阵A3的维数是100×20,则计算(A1A2)A3和A1(A2A3)所需要的乘法次数分别为15 000次和21 000次。通过这样的分析和要求,可以将学生的注意力从纯粹的数学性质证明转移到算法设计上,此时可以要求学生课下通过自学去编写相应的程序实现,可以采用递归、动态规划和备忘录算法分别实现。

(3) 鸽笼原理。鸽笼原理是组合数学上的一个经典结论,在离散数学中的最短路径、关系的闭包运算中需要用到。然而,许多教师在授课时,仅仅是把鸽笼原理和相关应用进行简单的介绍,不再进行深入分析。在授课过程中,除了介绍相关原理外,更注意鸽笼原理与程序设计技巧的相关结合。例如,授课过程中引入下面的例子:给定n个实数,求这n个实数在数轴上相邻2个数之间的最大差值,设计解最大间隙问题的线性时间算法。该问题其实并不复杂,最简单的思路是将给定的数进行排序,然后将排序后的数组扫描一下,得到2个数之间的最大间隙。问题复杂在要求的时间复杂度上,要求在O(1)时间内完成,而现在最快的排序算法时间复杂度为O(nlogn),因而该思路不满足题目的要求。授课中,将鸽笼原理的思想与程序设计结合起来,这就需要设计相应的鸽子和笼子。假设输入了n个数字,除去最大和最小2个元素外,剩余n-2个元素,如果将这n-2个数字分配到n-1个区间里,根据鸽笼原理,则至少有一个区间是空的。而分配在区间内部2个元素的差一定小于区间的宽度,因此,最大间隙是一定存在的。可以通过扫描空区间左边非空区间的最大值和右边非空区间的最小值的差得到最大间隙。介绍完实现思路后,具体的程序可以让学生去实现。通过这样的训练,学生不仅掌握了鸽笼原理,还提高了程序设计的技巧。

(4) 容斥原理。容斥原理是计数问题中的典型问题,授课过程中大部分教师将重点放在容斥原理的应用上[9-12]。在授课过程中,除了考虑容斥原理的应用外,可将更多的注意力放在容斥原理的证明上。在容斥原理的证明过程中,需要用到数学归纳法。授课过程中,对数学归纳法的机理进行深入分析,将数学归纳法与递归算法进行对比、分析,发现数学归纳法与递归算法非常相似。基于这样的分析,可以有效解决学生在学习递归算法时的困惑。如果学生容易接受,可以进一步分析递归算法的缺点,从而引出动态规划算法和备忘录算法,这可以让学生课后自行学习。

3 结语

对新工科教育中面向实践能力培养的离散数学授课模式进行了介绍,通过实践取得了较好的效果。学生在近3年的程序设计竞赛、ACM程序设计大赛中,均取得了较好的成绩。在后续的教学工作中,教学团队将进一步挖掘离散数学的相关知识点与程序设计的结合,让学生在学习离散数学这门课程的同时,尽可能提高程序设计能力和解决问题的思路。

参考文献(References)

[1] 左孝凌.离散数学的形成、发展及其在计算机科学中的作用与地位[J].自然杂志,1984,7(6):414-417.

[2] 张小峰,赵永升,杨洪勇,等. 离散数学[M]. 北京:清华大学出版社,2016.

[3] 张小峰, 蔡春波, 李秀芳,等.基于程序设计能力培养的离散数学教学改革[J].计算机教育,2015(2):44-47.

[4] 张小峰,李仁璞,邹海林.面向思维培养的离散数学教学模式[J].计算机教育, 2012(13):72-75.

[5] 李秀芳,张小峰,杨洪勇,等.离散数学知识解析与习题解答[M].北京:清华大学出版社,2017.

[6] 叶青,米春桥,唐波.地方应用型本科院校离散数学研究性教学改革与实践[J].大学数学, 2016, 32(6):53-57.

[7] 邓秀勤,李文洲,刘海林,等.基于计算思维能力培养的离散数学课程教学改革探索[J]. 大学数学,2017,33(1):75-79.

[8] 廖伟志,李文敬,王汝凉.基于培养学生计算思维的任务驱动式“离散数学”教学模式研究[J].计算机教育,2009(21):93-95.

[9] 曹建芳,赵青杉,陈立潮,等.面向计算思维能力培养的离散数学教学模式研究[J].高师理科学刊,2014(2):79-81.

[10] 汪荣贵,王晓华,杨娟,等.离散数学及其应用[M].北京:机械工业出版社,2017.

[11] 傅彦,徐洁,吴跃.计算机专业主干课程建设与教学改革[J].电子科技大学学报(社会科学版),2002(4):103-105.

[12] 陈光喜,古天龙.“离散数学”精品课程教学改革实践[J].桂林电子科技大学学报,2007, 27(4):300-302.

实验教学示范中心建设