基于Matlab/Simulink的TORA系统仿真实验

赵海滨, 刘 冲, 陆志国, 颜世玉, 于清文

(东北大学 机械工程与自动化学院, 辽宁 沈阳 110819)

具有旋转激励的平移振荡器(translation oscillators with rotating actuator,TORA)最早来源于双自旋航天器,用来研究其共振俘获现象[1-4]。TORA由一个能够做圆周运动的小球固定在一个与弹簧连接的小车上组成。TORA系统有2个自由度,但只有1个控制输入,因而是一种典型的欠驱动机械系统。

TORA系统作为非线性控制器设计的基准系统,常用的控制方法有无源法[5]、反步法[6]、基于能量的控制法[7-8]和滑膜控制法[9]等。基于能量的控制法和PD控制法是一致的。本文首先对TORA系统的动力学方程进行分析,然后利用Matlab/Simulink建立TORA系统的仿真实验平台,利用PD控制器对系统进行控制,仿真和研究了摩擦力对系统的影响。通过仿真模型,向学生完整地展示系统的仿真过程,能够加深学生对TORA系统的理解,激发学生的学习兴趣,有助于欠驱动系统的理论和实验教学。

1 TORA系统

TORA系统如图1所示。小球在输入转矩的控制下转动,通过小球和小车的耦合作用,对小车的位置进行控制。

图1 TORA系统的结构

采用拉格朗日方程法进行TORA系统的动力学建模[10]如下:

(1)

(2)

式中:m为小球的质量；r为小球的转动半径；M为小车的质量；k为弹簧的倔强系数；J为小球关于其质心的转动惯量；x为小车的位移；θ为小球与竖直向下方向的角度；f为小车受到水平面上的摩擦力；τ1为旋转小球的输入转矩。

将式(1)和(2)写成矩阵形式为

(3)

TORA系统的小车和小球是在水平面内运动,系统的势能P(q)为弹簧的弹性势能

(4)

TORA系统的向量G(q)和势能P(q)的关系为

(5)

TORA系统的总能量E(包括动能和势能)为

(6)

2 PD控制器

TORA系统中,小车在水平面运动时,小车和水平面会存在摩擦力。摩擦力会阻碍小车的运动,本文采用的摩擦力为

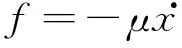
(7)

其中参数μ为摩擦系数。对于TORA系统,PD控制器和采用基于能量的控制方法是一致的。本文采用小球转角的PD控制器为

(8)

3 仿真实验平台

Matlab软件已经广泛应用于动态系统仿真,既可以用于连续系统和离散系统,也适用于线性系统和非线性系统[11-12]。Simulink功能强大、使用简单方便,是Matlab软件的重要软件包。根据TORA系统的动力学方程,采用Matlab/Simulink软件建立仿真模型。由于TORA系统的动力学方程比较复杂,不适合采用普通Simulink模块来建立模型,因而采用M-函数和积分模块等来建立模型,如图2所示。

图2 TORA系统仿真实验

M-函数为Simulink中用户自定义功能模块库中的Matlab Fcn模块。

TORA模块内的代码如下:

function [dd, E]= fcn(xdthd, xth, mu, tau1)

M=1.3608; m=0.096; k=186.3;

r=0.0592; J=0.0002175;

x=xth(1); th=xth(2); xd=xdthd(1); thd=xdthd(2);

d11=M+m;

d12=m*r*cos(th);

d21=m*r*cos(th);

d22=m*r^2+J;

D=[d11, d12; d21, d22];

C=[0, -m*r*thd*sin(th); 0, 0];

G=[k*x; 0];

f= -mu*xd;

dd=D([f; tau1]-C*[xd; thd]-G);

E=0.5*[xd,thd]*D*[xd; thd]+ 0.5*k*x^2;

输入值mu为摩擦系数,tau1为输入力矩,输出值E为按公式(6)计算的总能量。

PD模块内的代码如下

function tau = fcn(xdthd, xth)

th=xth(2);

thd=xdthd(2);

kp=0.07; kd=0.0023;

tau= -kp*th -kd*thd;

程序中的参数kp和kd为PD控制器的参数,摩擦系数μ用“mu”表示，输出力矩为tau。在图2中,积分模块的初始值由外部输入,手动开关Manual Switch在PD控制器和无控制输入之间进行切换,通过To Workspace模块将运行结果保存在工作空间中。

4 仿真设计实例

在仿真过程中,采用变步长的ode45算法,最大步长为0.0001 s。采用的TORA系统参数[2]为:

M=1.360 8 kg,m=0.096 kg,k=186.3 N/m,

r=0.059 2 m,J=0.000 217 5 kg/m2

4.1 实例1

通过手动开关模块将TORA系统的控制输入设置为0,摩擦系数μ=0,则系统的总能量保持不变。小车的初始位置为0.01 m,即初始状态为

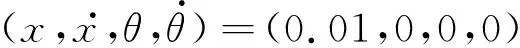
仿真时间为20 s,结果如图3所示。小车的位移在弹簧的弹力作用下周期运动,小球做圆周运动。

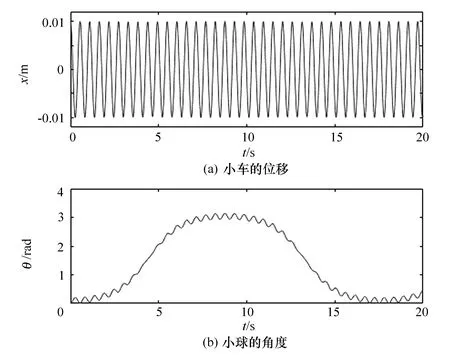
图3 实例1的仿真结果

4.2 实例2

将TORA系统的控制输入设置为0,摩擦系数μ=0.1,小车的初始位置为0.02 m,即初始状态为

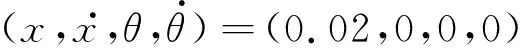
仿真时间设置为50 s,结果如图4所示。小车的位移做周期运动,小球做圆周运动。由于摩擦力的作用,小车的最大位移不断减小,系统的总能量逐渐减小。

4.3 实例3

图4 实例2的仿真结果

在PD控制器的作用下,小车的位移和小球的角度都趋近于0,小球的力矩和系统的总能量也趋近于0,系统的状态趋近于稳定状态，即：

5 结论

通过对TORA系统的动力学进行分析,利用PD控制器进行控制,采用Matlab/Simulink建立系统的仿真实验平台。利用该平台,可以非常容易地分析不同参数条件下系统的结果,把复杂的动力学模型进行简单、直观的展示,有助于学生对TORA系统的全面理解,为欠驱动系统理论的教学和实验提供方便。该仿真模型,还可以作为检验不同控制算法的基准平台。

参考文献(References)

[1] Liu Y, Yu H. A survey of underactuated mechanical systems[J].IET Control Theory and Applications, 2013,7(7):921-935.

[2] Bupp R T, Bernstein D S, Coppola V T. A benchmark problem for nonlinear control design[J].International Journal of Robust Nonlinear Control,1998,8(4/5):307-310.

[3] Bupp R T, Bernstein D S, Coppola V T. Experimental implementation of integrator backstepping and passive nonlinear controllers on the RTAC testbed[J].International Journal of Robust and Nonlinear Control, 1998,8(4/5):435-457.

[4] Olfati-Saber R. Normal forms for underactuated mechanical systems with symmetry[J].IEEE Transactions on Automatic Control, 2002,47(2):305-308.

[5] Jankovic M, Fontaine D, Kokotovic P V. TORA example: cascade-and passivity-based control designs[J].IEEE Transactions on Control Systems Technology,1996,4(3):292-297.

[6] 高丙团,贾智勇,陈宏钧,等.TORA的动力学建模与Backstepping控制[J].控制与决策,2007,22(11):1284-1288.

[7] 高丙团.TORA的动力学建模及基于能量的控制[J].自动化学报,2008,34(9):1221-1224.

[8] 武宪青,何熊熊.欠驱动基准系统的约束控制[J].控制理论与应用,2015,32(12):1692-1697.

[9] Xu R, Ozguner U. Sliding mode control of a class of underactuated systems[J].Automatica,2008,44(1):233-241.

[10] 蔡自兴.机器人学[M].2版.北京:清华大学出版社,2009.

[11] 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].2版.北京:清华大学出版社,2011.

[12] 赵海滨.MATLAB应用大全[M].北京:清华大学出版社,2012.