基于AMR的环境磁场测量仪设计与应用
2018-06-05王晓娜王彦霞宋世德
林 淮, 王晓娜, 王彦霞, 宋世德
(1. 大连理工大学 物理学院, 辽宁 大连 116024;2. 大连理工大学 土木工程学院, 辽宁 大连 116024)
目前磁场测量的方式众多,磁场测量的范围也已达到10-15~103T[1]。在此范围内的磁场测量传感器可分为低强度、中强度以及高强度磁场传感器[2]。低强度磁场传感器通常检测 1 μG 以下的磁场,中强度磁场传感器通常检测 1 μG~10 G 磁场,高强度磁场传感器检测范围通常在 10 Gs 以上[3]。日常生活中的环境磁场,主要源于地磁场及建筑钢构,一般在中强磁场强度的范围内。在主要利用的原理包括:霍尔效应、磁通门、AMR等。AMR因其响应时间短、测量精度高等优势,成为中强磁场测量仪器中的常用传感器。
传统的磁场测量仪器结构复杂,产生的磁场对测量结果产生较大影响,仪器的使用地点也受到限制;霍尔式的磁场测量仪器则要求手持操作,不易实现快速且精确的测量,并且传感器探头较为脆弱,不利于室外测量与长期使用。
针对传统磁场测量仪器的缺陷,本文基于AMR传感器设计环境磁场测量仪,通过电路系统进行信号调理,抑制交变磁场信号及噪声的干扰,使用单片机进行信号的计算,以及环境中稳恒磁场磁感应强度大小的显示。仪器通过电路简化操作的同时,也与外部机械构造一同确保测量的精度与稳定性。
1 磁场信号采集原理
1.1 各向异性磁阻传感器(AMR)原理
HMC1021z磁阻传感器中的硅片上镀有坡莫合金,构成惠斯通电桥。当环境磁场的磁感应强度在±6×10-4T之内、工作电压Ub=5V时,磁阻传感器输出电压Uout与敏感轴方向磁感应强度B变化呈线性关系,即[4]:
Uout=U0+kB
(1)
式中U0表示磁阻传感器电桥存在的偏置电压。
传感器的S/R端可以对磁畴进行复位,保持传感器的灵敏度与高精度。
1.2 环境磁场探测原理
该磁场测量仪器测量环境中稳恒磁场的磁感应强度大小及磁倾角大小,从而描述特定的磁场。环境中稳恒磁场的磁感应强度B可分解为水平分量B1以及竖直分量B2,见图1。
(2)
(3)
公式中θ代表磁场磁倾角大小。由于仪器使用单轴各向异性磁阻传感器进行测量,因此,测量过程中需要分别测量磁场水平分量(水平方向磁感应强度最大值)、竖直分量的磁感应强度大小。

图1 磁场示意图
2 系统设计部分
2.1 全局设计
测量系统的主要模块见图2。为了实现仪器的便携性,并且减小电源产生的磁场对测量的干扰,电源部分采用2节电池连接,提供正负±9 V的双电源为仪器供电。对于传感器及单片机所需的5 V电压,使用7805稳压芯片将9 V降为5 V。
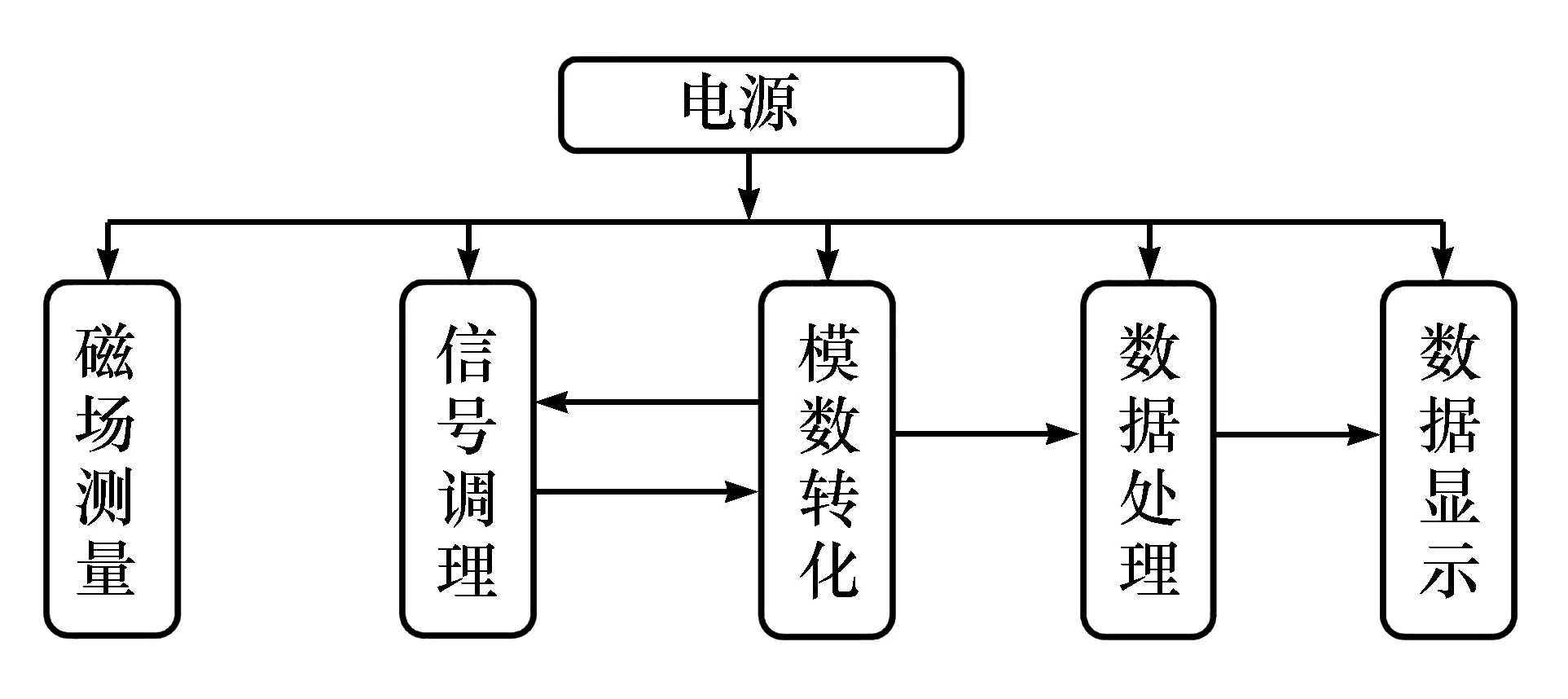
图2 系统模块框图
2.2 信号调理部分
在5 V直流供电的条件时,传感器敏感轴方向感应到1×10-4T磁感应强度,输出5 mV电压,而一般环境磁场强度约为0.5×10-4T,其分量对应的输出电压更加微小。由于传感器输出的是相当小的电压信号,需要将传感器输出信号进行调理后送入单片机模块处理[5]。为了数据处理以及抑制零点漂移,在传感器的输出端使用AD620对电压信号进行500倍的差分放大,AD620具有高精度、低功耗、低失调漂移等特性,常用于微小信号的一级放大。
为了抑制传感器的噪声及特殊环境可能存在的交变磁场,仪器的二级电路采用二阶有源低通滤波电路对信号进行处理。Sallen-key结构是电路设计中最常用的有源低通滤波器电路结构[6],其电路结构见图3。
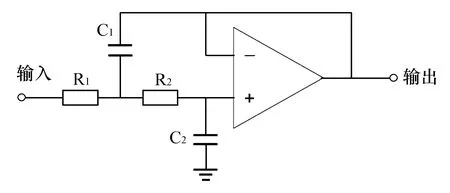
图3 Sallen-key结构的有源低通滤波器
在保证响应时间及滤波效果的前提下,根据截止频率为1 Hz的指标选择滤波器类型,再通过设计表中的元器件参数值即可完成滤波器的设计[7]。
图3中的运算放大器选择常用的高精度运放OP07,它拥有高开环增益、低失调偏移电压、低噪声的特性,适用于传感器的信号处理[8]。
考虑到AD7705模数转换器输入电压在0~5 V之间,而磁场方向与传感器敏感轴方向夹角大于90°时电压信号有可能出现负值。5 V供电时,-1×10-4T磁场输出-2.5 V(信号放大500倍),因此电路中使用OP07运算放大器搭建加法运算电路。TL431为信号提供2.5 V的偏置,在±1×10-4T(一般环境强度约0.5×10-4T)的磁场范围内,保证仪器的正常使用。
放大、滤波后的电压信号使用AD7705模数转化芯片,将电压信号数字化,由单片机进行采样与计算,最终在LCD1602显示屏上进行显示。
2.3 软件仿真
为了检验电路设计部分的性能,可使用Multisim对信号调理部分进行仿真, 完成电路的瞬态分析和稳态分析[9]。其中函数发生器模拟传感器输出,使信号依次经过放大、滤波、加法电路,并使用波特图仪对信号进行分析。仿真电路见图4。波特图仪模拟结果见图5。

图4 仿真电路
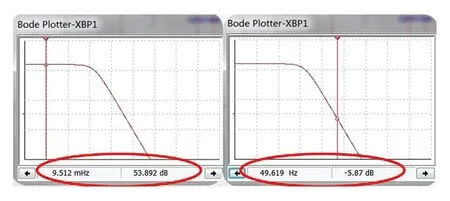
图5 波特图仪模拟结果
从图5中可以看出,对于接近稳恒的信号,电路能产生53.892 dB的增益,而对于约50 Hz的干扰信号则产生5.87 dB的衰减,能够很好地减少噪声及其余交变干扰,对环境稳恒磁场进行测量。
2.4 整体构造
整体上看仪器分为两大部分,电池位于单片机下方,传感器所在部分搭配木材与亚克力等材料制作的水平、竖直调节装置,在减小干扰并且易于操作的同时,保证测量时装置的精确度及稳定性。搭建完成的实物图见图6。
3 单片机编程
仪器综合了单片机控制的低成本优势和软硬件的通用性,使用简便、操作直观[10]。仪器中的单片机对电压信号进行采集,对未标定的仪器,LCD1602显示屏上将显示实时电压值;而将标定后的B-U曲线加入程序中进行编程,显示屏上即可实时显示采集到的磁感应强度大小,并同时输出测量过程中磁感应强度的最大值。程序流程图见图7。

图6 测量系统实物图

图7 程序流程图
4 实验结果与分析
4.1 仪器标定
装配完成的仪器还需要在其量程范围内,确定输出的电压U,与传感器易磁化方向接收到的磁感应强度B之间的关系,因此需要对制作完成的仪器进行标定。
首先借助亥姆霍兹线圈对仪器的B-U直线斜率进行标定。亥姆霍兹线圈能在其公共轴线中点附近产生较广的均匀磁场区,故常用于较弱磁场的计量标准[11]。亥姆霍兹线圈公共轴线中心点位置的磁感应强度可表示为[12]
(4)
其中N为线圈匝数;I为流经线圈的电流强度;r为亥姆霍兹线圈的半径;μ0为真空磁导率。
标定过程中,将仪器的传感器模块放置在亥姆霍兹线圈轴线的中点处,并且使测量方向和公共轴线垂直。改变I的大小,得到确定的磁感应强度值。由于仪器标定时会受到恒定环境磁场的干扰,因此首先需要通过亥姆霍兹线圈磁感应强度的改变量ΔB,以及未标定的仪器显示的电压改变量ΔU确定U-B直线的斜率k,即
(5)
标定结果见图8,使用最小二乘法得到斜率k=3.667×10-4,截距b=-0.119 7,相关系数R=0.999 9。
除了亥姆霍兹线圈产生的磁场外,B-U拟合直线的截距受到环境磁场以及仪器内部失调电压的影响,产生恒定的偏置,故有
B=kU+b
(6)
此时需要对内部失调电压进行补偿,使得测得的磁感应强度与实际环境磁感应强度相同。
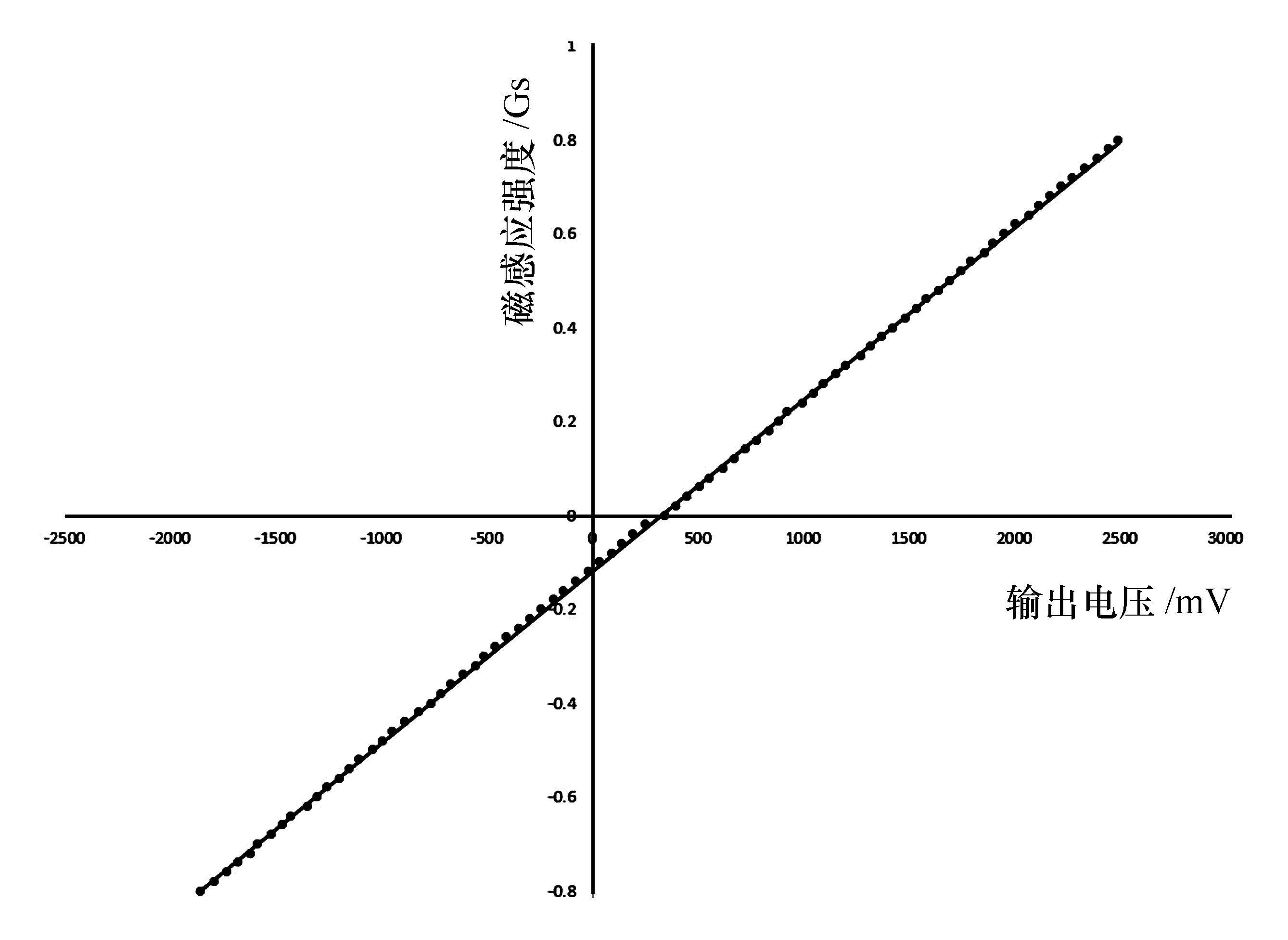
图8 标定数据图
撤去亥姆霍兹线圈,水平放置传感器部分,此时测得的磁感应强度可表示为
B1=Be+C
(7)
式中B1表示仪器显示的磁感应强度,Be表示环境磁感应强度,C表示仪器失调电压产生的偏置,可看作一个常数。
此时利用底座上的转盘将仪器水平旋转180°,测得磁感应强度B2为
B2=-Be+C
(8)
由式(6)、(7)可得失调电压准确值为
(9)
因此,修正后的U-B曲线可表示为
B=kU+b-C
(10)
将标定的数据代入式(10)可得最终B-U关系
B=0.0003667U-0.04603
(11)
4.2 测量结果对比
标定完成的仪器可以分别测量水平与竖直方向上的磁感应强度分量及合成环境中的总磁感应强度。在5个不同地点,使用仪器与高精度的Lakeshore 425高斯计对比测量,结果见表1。

表1 测量结果对比
5 结语
本文在分析环境磁场测量仪器的技术关键及技术难点的基础上,设计并制作出基于各项异性磁阻传感器的磁场测量仪。该仪器能够有效地测量环境磁感应强度的大小及磁倾角的大小。1×10-4T的量程及较高的精度,能够满足室内外环境磁场测量的要求,在实验教学及磁场监测等方面具有实际意义。
参考文献(References)
[1] 姜智鹏,赵伟,屈凯峰.磁场测量技术的发展及其应用[J].电测与仪表,2008,45(4):1-5.
[2] Caruso M J, Smith C H, Bratland T, et al. A New Perspective on Magnetic Field Sensing[J].Sensors,2010,15(12):1-16.
[3] 潘启军,马伟明,赵治华,等.磁场测量方法的发展及应用[J].电工技术学报,2005, 20(3):7-13.
[4] 王国余, 张欣, 景亮. 新型磁阻传感器在地磁场测量中的应用[J]. 传感器技术, 2002, 21(10):43-45.
[5] 刘莹,祝学云,范文. 检测技术课程设计型实验系统研制[J].实验技术与管理.2015,32(6):137-138.
[6] 林斯波,葛愉成. 基于Sallen-Key 滤波器的主成形放大电路的研究[J]. 2015,35(4):408-416.
[7] Williams A B. Analog Filter and Circuit Design Handbook[M].America:McGraw-Hill Education,2014.
[8] 王晓娜,宋世德. 基于NI ELVISⅡ平台实现低通滤波器的设计与性能分析[J]. 实验技术与管理, 2017, 34(9):72-75.
[9] 颜芳,宋焱翼,谢礼莹,等. 基于Multisim的电路原理课程仿真实验设计[J].实验技术与管理,2013,30(5):59-62.
[10] 倪文彬,陆广华,叶留芳. 基于STM32单片机的三轴实验平台设计[J].实验技术与管理,2016,33(12):163-166.
[11] 鲁绍曾.现代计量学概论[ M].北京:中国计量出版社, 1987:492-493.
[12] 贾玉润, 王公冶, 凌佩玲.大学物理实验[ M].上海:复旦大学出版社, 1987:256-258.
