基于激光光斑中心检测的改进算法

秦运柏, 徐汶菊, 朱 君

(广西师范大学 电子工程学院, 广西 桂林 541004)

激光光斑图像[1]因为各种干扰,眼睛不能精确对其定位。借助物理手段可以比较精确地找到光斑的中心点,但费时费力,而且对物理器材的要求精准度很高。用软件实现定位算法相对速率更快[2],精准度比较高[3-5]。在最小二乘原理[6]的基础上,孔兵等2人提出了圆拟合算法[7],该算法可以在干扰很小的情况下对光斑中心进行较高精度的定位,还可以检测出半径大小。所以该算法不仅具有很快的计算速度, 而且具有很高的可操作性和实时性，但是在实际使用中对光斑图像的质量要求比较高。吴泽楷等[8]提出了一种基于改进圆拟合算法的激光光斑检测算法,该算法定位光斑中心虽然有很高的精度,但要经过多次迭代,需要的时间比较多。Chan等[4]提出了TV(total variation)修复算法的雏形,并与其他修复算法相比,TV修复实现较为简单,能很好地修复图像的局部模糊。在传统的圆拟合激光光斑中心定位算法上其精度有一定的提高,但是却限制了在实际测量中在噪声干扰下的圆拟合算法的计算。

本文在传统圆拟合算法[7-10]的基础上做了改进。首先,光斑图像通过预处理[11]去掉日常因素的干扰,再通过改进的TV滤波算法进行较好的滤波去噪,最后通过圆拟合算法进行精确定位。

1 理论分析

1.1 圆拟合法

在圆拟合算法中,最为经典的就是有利于最小二乘法对光斑的边界点的坐标进行拟合,能更大程度地模拟激光光斑轮廓。

圆的标准方程为

(x-a)2+(y-b)2=r2

(1)

取残差εi为

εi=(xi-a)2+(yi-b)2-r2

(2)

式中,i∈E,E为光斑图像所有边界点的集合；(xi,yi)为光斑图像所有边界点的坐标。

由此可得残差平方和函数Q为

(3)

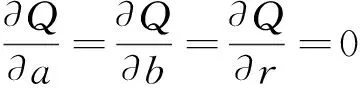
(4)

(5)

(6)

其中各参数可用下式表示:

(7)

式中I为集合。化简整理有:

(8)

(9)

由上可推得参数a、b、r的表达式：

(10)

(11)

(12)

虽然圆拟合算法在计算光斑中心坐标的过程中很复杂,但是对光斑图像的边界点只循环计算1次,就可以得出它的各个参数值,包括光斑中心点的坐标和光斑的半径,所以整个计算过程还是很快的。

1.2 TV修复理论算法

Chan和Shen在2002年提出了基于TV修复算法的雏形[12]描述如下:通常在一个完全的图像区域x=(x1,x2)∈Ω上定义了一个理想的图像u0=u0(x)。但是,由于其他因素,其图像采集、传输并不是完美的,其子集D⊆Ω,代表了D上的图像信息缺失。令E=Dc=Ω/D,如图1所示。

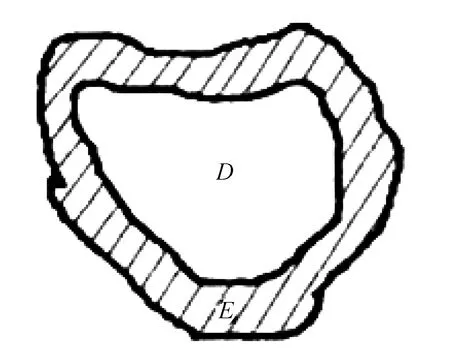
图1 区域Ω示意图

则定义修复函数为

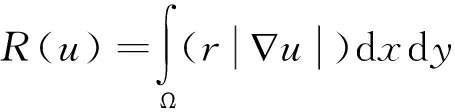
(13)

且满足噪声约束:

(14)

其中, 外邻域面积就是A(E),高斯白噪声就存在阴影内的图像内；u为图像；σ2为白噪声的标准方差；r为非负的实函数。

可寻找一个适合的函数r,来获得图像边缘的处理的良好效果。在边缘上，u是一个冲击函数δ，因而要求函数r有限，即:

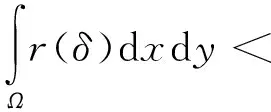
(15)

若函数r(s)展开,可获得其形式:

r(s)=sa+低阶展开项(S为总迭代次数)

(16)

式(15)要求s→时r(s)有限,因此a≤1。选取a=1,此时TV修复技术的模型就是公式(13)。把Lagrange乘子应用到公式(13)可得新的函数为

(17)

式中，λ为拉格朗日待定系数。

根据Euler-Lagrange方程,若Jλ(u)有最小的u,必有:

-

(18)

其中:

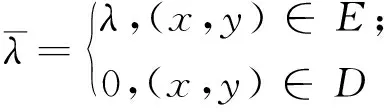
相对应的最速下降方程为

(19)

(20)

-

(21)

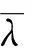
在图像里去掉高斯白噪声,由(20)式有

(22)

即为TV模型的图像修复基本公式。

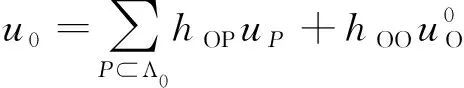
用下面的迭代公式替换原来的迭代公式:

最终算法步骤如图2。

图2 TV修复算法流程图

在迭代初期，选用较大α值，以确保边界信息可以充分扩散，然后在使用当前α值迭代至收敛时，逐步减小α值，使边界有较好的修复效果。

(1) 读取整个区域的图像信息；

(2) 令α=5；

(3) 对Ω区域内的每个像素,按照(13)、(14)、(15)、(22)公式的顺序进行迭代,更新每个像素值,当图像更新值与原值的差值d小于阈值c时停止当前迭代,进入下一个循环；

(4) 令α=α/5,重复第3步骤。在经过4轮不同α值的循环后,当当图像更新值与原值的差值a小于阈值y或总的迭代次数超过迭代上限(2 500次)时停止迭代；

(5) 最终的迭代结果即为修复结果。

2 实验方案

2.1 流程

本文的改进方案是在圆拟合的基础上进行改进的,并结合了传统的TV滤波原理,在圆拟合算法之前先对图像进行预处理。改进方案的算法流程见图3。

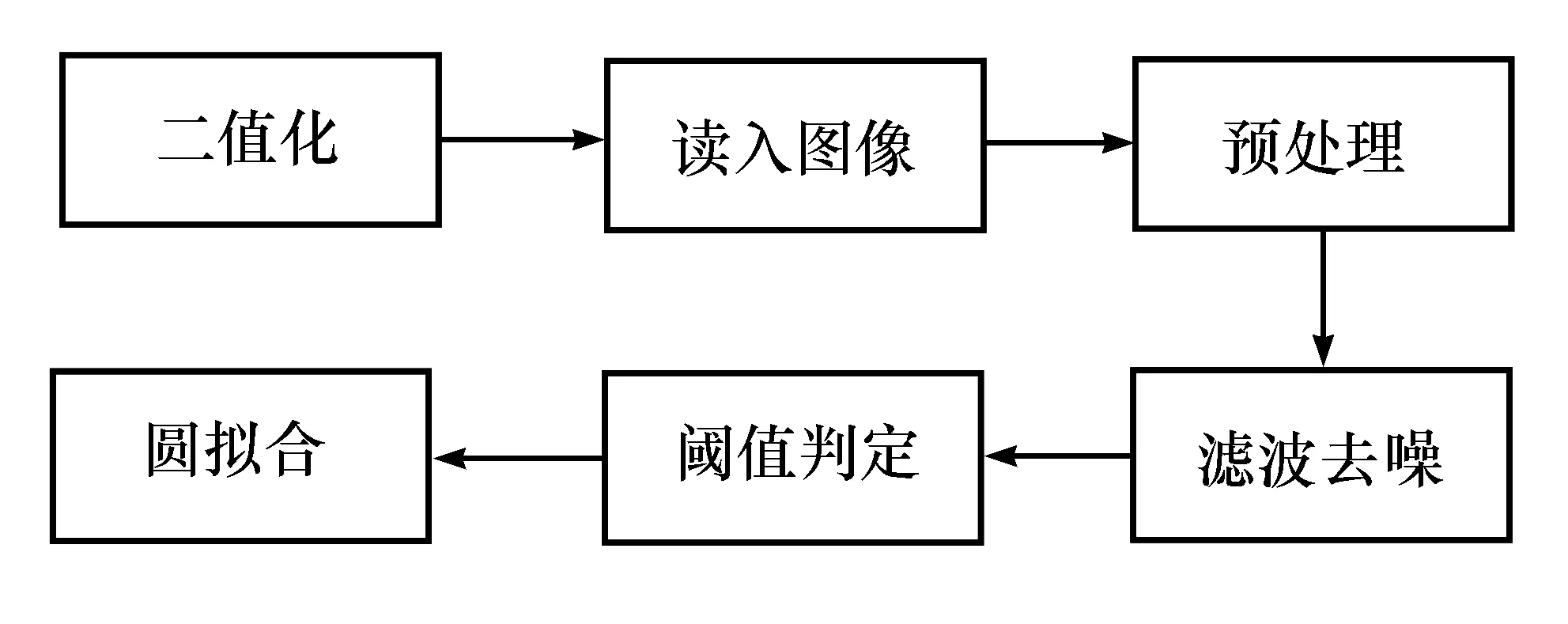
图3 改进方案的算法流程

预处理用于随机噪声的影响,二值化分割用于凸显光斑轮廓,滤波去噪进一步减弱图像中的噪声影响,然后圆拟合对光斑进行中心定位。该算法经过多次迭代提高了光斑坐标的精确度。

2.2 改进算法及特性分析

若一个白噪声n(k)是高斯的,那么其所有的有限边界分布是高斯的。日常图像处理中,最为平常不过的就是带有高斯分布的噪声。故本文加入的噪声类型就是高斯白噪声。

为了验证本文所采用的滤波方法的有效性,本文在Matlab2010上应用自适应TV修复技术的方式对加入高斯白噪声的同一副光斑图像进行滤波测试。对比了几种滤波效果,有自适应TV修复技术、中值滤波(median filtering,MF)、均值滤波(averge filtering, VF)的比较,结果见图4。

从实验结果可以看出,当对被污染图像进行滤波时,中值滤波和均值滤波输出图像的光斑边缘开始模糊，并且出现了大量斑点,而且轮廓模糊,表明它们对被高斯白噪声污染的图像的滤波效果不够理想; 而采用本文滤波算法对光斑图像进行滤波,能有效地抑制光斑图像的噪声,同时还能较为有效地保留图像边缘细节,效果良好。

图4 滤波效果比较

3 结果与数据分析

本文算法的核心在于先对光斑图像滤波,然后进行圆拟合,最后计算光斑中心。采用Matlab进行实验,可以对比计算出来的点中心坐标和原图中心的坐标,从而可知定位光斑中心精度。

图5是通过圆拟合法对图4的一系列光斑进行圆拟合的效果图。表1给出了利用圆拟合算法结合改进TV滤波方法进行中心定位的误差,可以看到自适应TV修复技术提供了更为准确的中心坐标。实际上，平常对于光斑图像的采集都是附带有干扰和噪声,用常见的滤波算法(如均值滤波和中值滤波)来操作光斑图像必然会产生过大的误差。这也是本文采用自适应的TV修复技术进行滤波的原因。

图5 圆拟合效果

本文通过采集一组大小约为 300像素×400像素的光斑图像 ,并对这组光斑图像进行编号为1、2、3、4、5。这组图像是具有相似形状 、灰度值和中心位置的光斑,然后它们被加入高斯白噪声,并被改进的自适应TV滤波算法进行滤波,最后被圆拟合算法进行中心定位。可以对比计算出来的点中心坐标和原图中心的坐标,从而可知定位光斑中心精度，结果见表1。

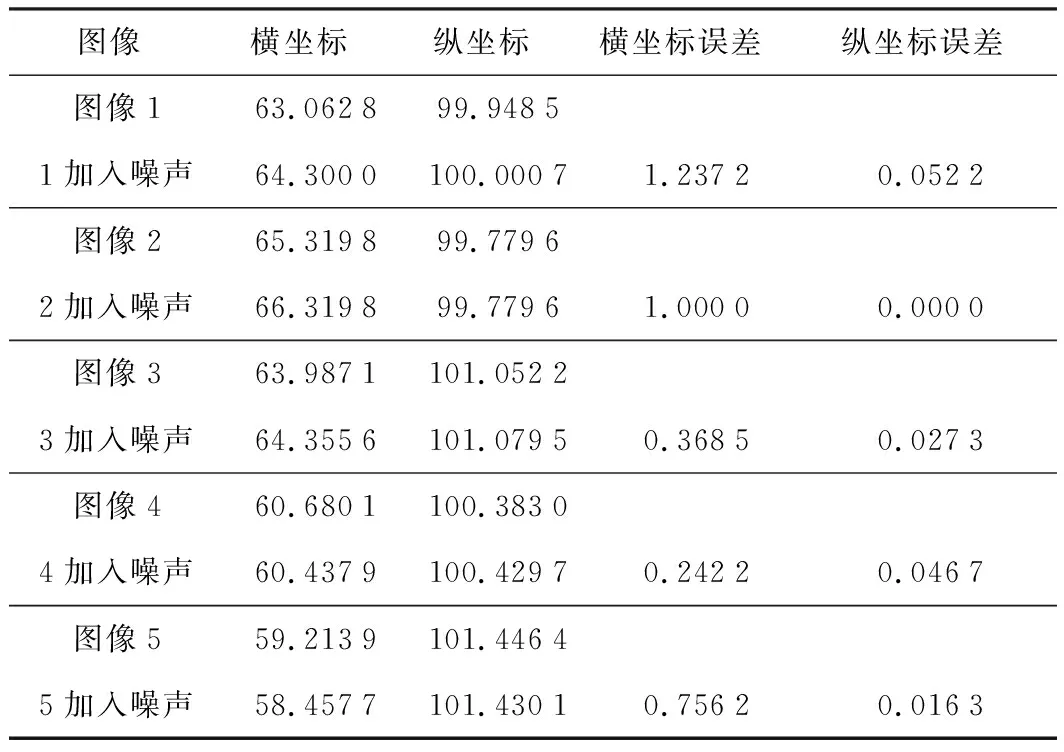
表1 对TV滤波方法图像进行中心定位的误差 像素

从表1的数据可以看出,在光斑夹杂噪声的情况下,光斑中心横坐标误差小于2个像素,而纵坐标误差在1个像素之内,这说明本文的算法具有较高的精度。

4 结语

均值滤波和中值滤波等虽然简单明了、运算快,但是这些传统的滤波算法适用的范围过窄,只在少量噪声的光斑图像中才会凸显传统滤波算法的优势，如果光斑图像带有大量的噪声和干扰,则测出的光斑中心坐标误差较大。自适应TV滤波对实际光斑的滤波效果更好,该算法结合圆拟合能取得较高的坐标精度，在有噪声情况下本文算法的定位误差在2个像素内,说明本文算法在实际应用过程中具有更强的抗干扰能力。

参考文献(References)

[1] Lu Z W, Liu X Y, Wang X, et al. High-precision small-scale laser focal spot measurements[J]. Laser & Particle Beams, 2013, 31(1):177-183.

[2] 谈凯德, 杨晶东, 薛皓天. 一种有效的激光光斑中心检测算法研究[J]. 控制工程, 2016,23(11):1813-1819.

[3] 黄浩, 詹玲. 一种光斑中心定位算法的研究与实现 [J ]. 小型微型计算机系统 ,2005,26(7):22-26.

[4] 魏振忠, 高明, 张广军,等. 一种光斑图像中心的亚像素提取方法[J]. 光电工程, 2009,36(7):7-12.

[5] 王丽丽,胡中文, 季杭馨. 基于高斯拟合的激光光斑中心定位算法[J]. 应用光学, 2012, 33(5):985-990.

[6] 陈明逵, 凌永祥. 计算方法( 工程类) [ M]. 西安: 西安交通大学出版社, 1992.

[7] 孔兵, 王昭, 谭玉山. 基于圆拟合的激光光斑中心检测算法[J]. 红外与激光工程, 2002, 31(3):275-279.

[8] 吴泽楷, 李恭强, 王文涛,等. 基于改进圆拟合算法的激光光斑中心检测[J]. 激光与红外, 2016, 46(3):346-350.

[9] Chan T F, Shen J. Mathematical models for local nontexture inpaintings[J]. Siam J Appl Math,2002,62:1019-1043.

[10] 穆娟. 利用圆拟合进行激光光斑中心检测[J]. 舰船科学技术, 2016(24):127-129.

[11] 张艳玲, 刘桂雄, 曹东,等. 数学形态学的基本算法及在图像预处理中应用[J]. 科学技术与工程, 2007, 7(3):356-359.

[12] Kenneth R Caslteman.数字图像处理[ M].阮秋琦，译.2版. 北京: 电子工业出版社, 2003.