基于相关分析法的脉冲响应辨识实验设计

刘 恒, 孙 晋, 邰凡彬, 张易晨

(南京信息工程大学 电子与信息工程学院, 江苏 南京 210044)

系统辨识是控制领域的一个十分重要分支。在多数情况下,被控对象的模型是不知道的,或者在正常运行期间模型的参数可能发生变化。在控制领域经常会碰到这样的问题,并且模型未知的被控对象很难得到合理控制。为了能更好地分析和控制被控对象,首先需要建立它的数学模型,即系统辨识[1]。单位脉冲响应函数中包含了系统所有的动力特性参数,提取系统的单位脉冲函数或频率响应函数是获取系统动态特性参数、进行系统辨识以及对系统进行有效监测与精确控制的前提[2]。相关分析法是目前普遍受到重视的一种辩识脉冲响应的方法,当系统存在噪声时,利用相关分析法辩识脉冲响应可以收到比较满意的效果[3]。相关分析法脉冲响应辨识广泛应用于大气温室效应建模[4]、地球物理电磁方法勘探的研究[5]、电机励磁绕线变形[6]等。目前,相关分析法辨识脉冲响应主要基于Matlab软件,通过软件产生m序列信号,激励待辨识系统,通过m序列信号和待辨识系统的输出计算,得到相关分析法辨识的脉冲响应[7-9]。仿真有一定的空洞性,不利于学生对辨识方法的各个节点响应的理解。鲜有文献报道硬件辨识实验[10]。本实验结合电子信息类学生的专业基础,利用仿真软件和实际硬件完成了实验介绍,将相关分析法辨识系统脉冲响应仿真通过硬件系统来实现,提高学生对系统辨识中m序列信号、卷积运算等相关知识的理解。

1 相关分析法原理

相关分析法辨识系统脉冲响应是经典辨识方法中的一种。如果有2个时间函数,其中一个总是在任何时刻的值总是以某种确定关系依赖于另一个函数的值,则这2个函数是时间相关的。m 序列的特性类似于白噪声,常在系统辨识过程中作为输入信号,通过对输入输出信号的互相关运算,就可以得到待测系统的脉冲响应。

m序列是循环周期为Np·Δt、自相关函数近似于δ函数的一种随机序列,其统计特性近似于白噪声。m序列的自相关函数Rm(τ)为:

(1)

式中,a为m序列的幅值,τ为时间常数,Δt为移位寄存器移位周期,Np为m序列的长度。Np足够大(选择Np使m序列的循环周期大于系统的过渡过程时间)。

设数据的采样时间等于m序列移位脉冲周期Δt,则Wiener-Hopf方程写成离散形式[11]为

(2)

当m序列的循环周期Np·Δt大于系统的过渡过程时间tr时,脉冲响应在时间大于Np·Δt后基本上衰减为零。

(3)

实际应用中,式(3)中,j小于Np,式(3)同样可表示为

(4)

式(4)中,M(j-τ)为离散后第j-τ个时刻的m序列信号,y(j)为第j时刻的系统激励后的测量输出。

系统输入和输出的时刻τ的相关函数可以通过对输入输出测量获得。结合式(1)和(2),将式(3)展开为

(5)

假设:

对于一个稳定的待辨识系统来说,C是一个有界常数,而且很小(当Np充分大时),根据式(4)和(5),则有[11]:

(6)

待辨识的二阶系统的传递函数为

时间常数T1=2.0 ms,T2=1.0 ms,静态增益K=5.0。二阶系统可以转换为

(7)

式中，ϖ02=1/(T1·T2)=500 000，

很显然,系统阻尼ξ大于1,系统过阻尼,不存在超调量。对应的单位阶跃响应h(t)为

(8)

式(8)中,M1和M2分别为:

随着t的增大,h(t)的后两项趋近于0,所以对应的稳态值为1,假定从t=0开始,达到稳定值的98%为过渡时间tr,根据式(8)可以得到:

(9)

求解式(9),得到过渡时间tr=9.2 ms。利用Multisim软件搭建待辨识二阶系统,二阶系统由运算放大器和电阻、电容构成,搭建的电路原理见图1。

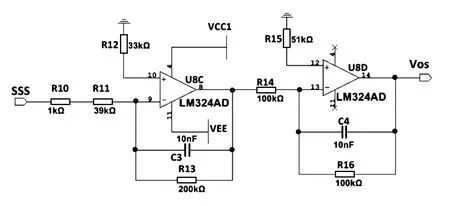
图1 二阶待辨识系统电路原理图

系统在ϖ=0 rad/s时,s=jϖ=0,对应二阶系统增益为5,此时幅频曲线幅度为20log(5)=13.979 4 dB,见图2。二阶系统有低通滤波特性,系统的带宽约为72 Hz,见图3。

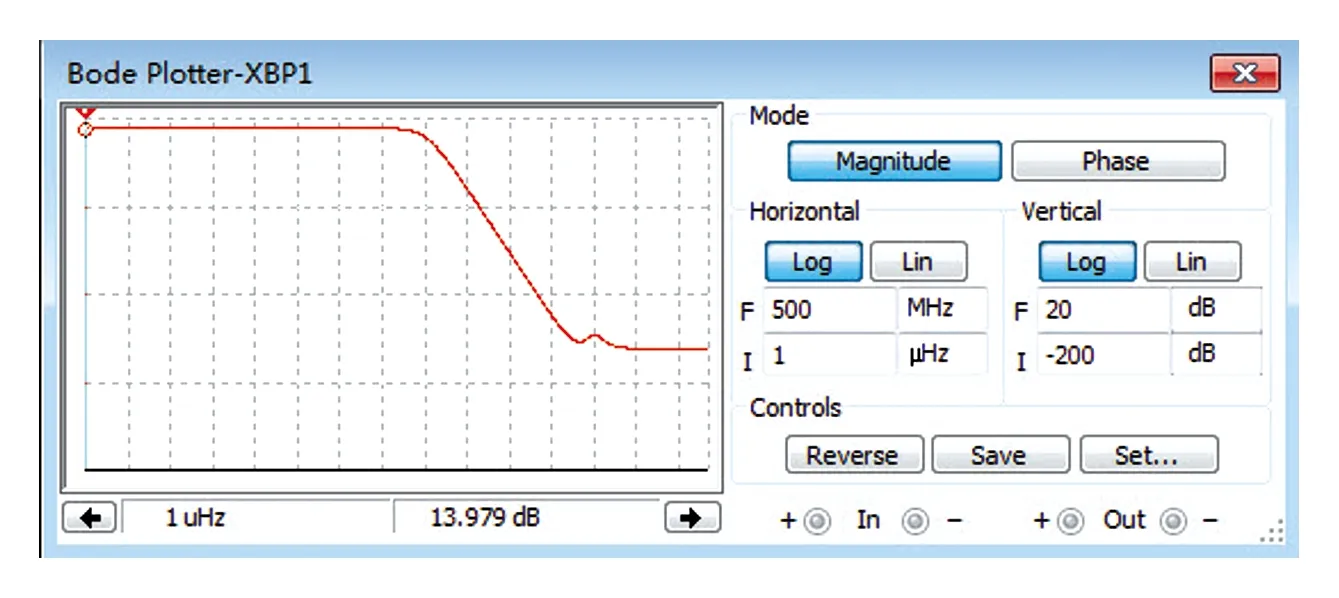
图2 系统对应的幅度-频率响应曲线(低频)

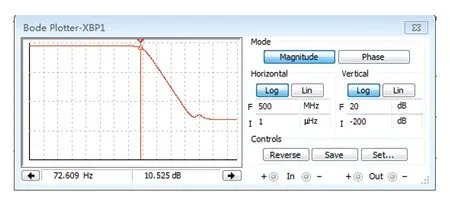
图3 系统带宽仿真估算

用m序列作输入信号辨识脉冲响应的步骤:

(1) 预估被辨识系统的过渡时间tr和系统的最高工作频率fmax,tr和fmax是选择m序列的重要依据,实验中tr=9.2 ms,fmax=72Hz。

(2) 在系统辨识中,激励输出数据必须尽可能多的包含系统动态特性的信息,这和输入信号的选择有很大关系。当系统的频率特性接近低通滤波特性时,m序列的参数Np和Δt应满足下述条件:

(10)

(Np-1)·Δt≥tr

(11)

根据式(10)有Δt≤1/216=4.63 ms。对于m序列的阶数N与参数Np之间存在如下关系：Np=2N-1。 利用m序列来激励二阶系统,通过系统的输出及激励信号的运算来达到辨识。根据相关分析法的理论推导,m序列阶数越高,对应的辨识精度越高,但辨识算法的卷积计算的时间越长,同时采样的周期也更长,使得辨识响应变慢。实验综合考虑后,结合式(10)和(11),选择了6阶m序列信号来激励二阶系统,Np=63,Δt=0.2 ms。通过对激励信号和响应信号进行采样,利用辨识算法得到系统的脉冲响应曲线。

2 辨识电路设计

辨识电路包括m序列产生电路和脉冲响应辨识电路。前者包括时钟电路、移位寄存器及控制电路、序列变换电路；后者包括二阶系统、电平抬升电路、主控电路、按键、数字显示屏,见图4。

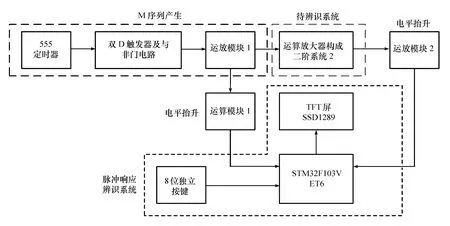
图4 辨识电路硬件电路模块

555定时器产生时钟信号,移位寄存器及控制电路由双D触发器及逻辑门构成,序列变换由运算放大器和电阻组成。待辨识二阶系统由运算放大器和电容、电阻构成,电平抬升电路均由运算放大器和电阻构成,主控制器为STM32F103单片机最小系统,数字显示屏为TFT屏SSD1289,8位独立按键。

2.1 M序列产生电路

时钟电路见图5，由555定时器LM555及直插电阻、电容、二极管构成。输出的方波信号高电平为+5 V,低电平为0 V。芯片采用5 V电源供电,调节电阻R1、R2、R3及电容C1就可以改变方波的频率和占空比。其中输出高电平时间tw1≈0.7(R1+R2+R3)C1,低电平时间tw2≈0.7(R2+R3)C1。设计的输出方波频率为5 kHz,对应周期为0.2 ms,仿真输出波形见图6,对应的硬件测试输出波形见图7,硬件测试与仿真一致,但电源提高到6 V,便于后续驱动触发器。

图5 时钟电路

图6 仿真时钟波形

m序列信号由1和0构成,通过移位寄存器和控制电路来实现。逻辑“1”的个数比逻辑“0”多1。一种6阶M序列信号,由6个移位寄存器组成。对应的m序列信号长度为63,序列信号的逻辑为{1,1,1,1,1,1,0,0,0,0,0,1,0,0,0,0,1,1,0,0,0,1,0,1,0,0,1,1,1,1,0,1,0,0,0,1,1,1,0,0,1,0,0,1,0,1,1,0,1,1,1,0,1,1,0,0,1,1,0,1,0,1,0}。对于6阶m序列的反馈系数(八进制)为103,147,155,有3种实现方式,对应二进制数为1000011、1100111、1101101。7位分别对应D0、Q1、Q2、Q3、Q4、Q5、Q6,0表示没有参与反馈,1表示参与了反馈。3种控制输出D0= Q5⊕Q6,D0= Q1⊕Q4⊕Q5⊕Q6,D0= Q1⊕Q3 ⊕Q4⊕Q6。在本项目中,没有采用异或门,采用与非门来实现异或门的逻辑功能。设计中,采用了2个2输入1输出与非门单元,1个8输入1输出与非门,1个3输入1输出与非门。没有全部采用二输入一输出的与非门,便于更好地可靠连线,保障信号发生器的功能。图8为由3片双D触发器和逻辑门电路构成的移位寄存器及控制电路，图9为其仿真输出波形,周期约为12.6 ms,刚好是周期0.2 ms的63倍,图10为实测的输出波形,与设计的期望一致。

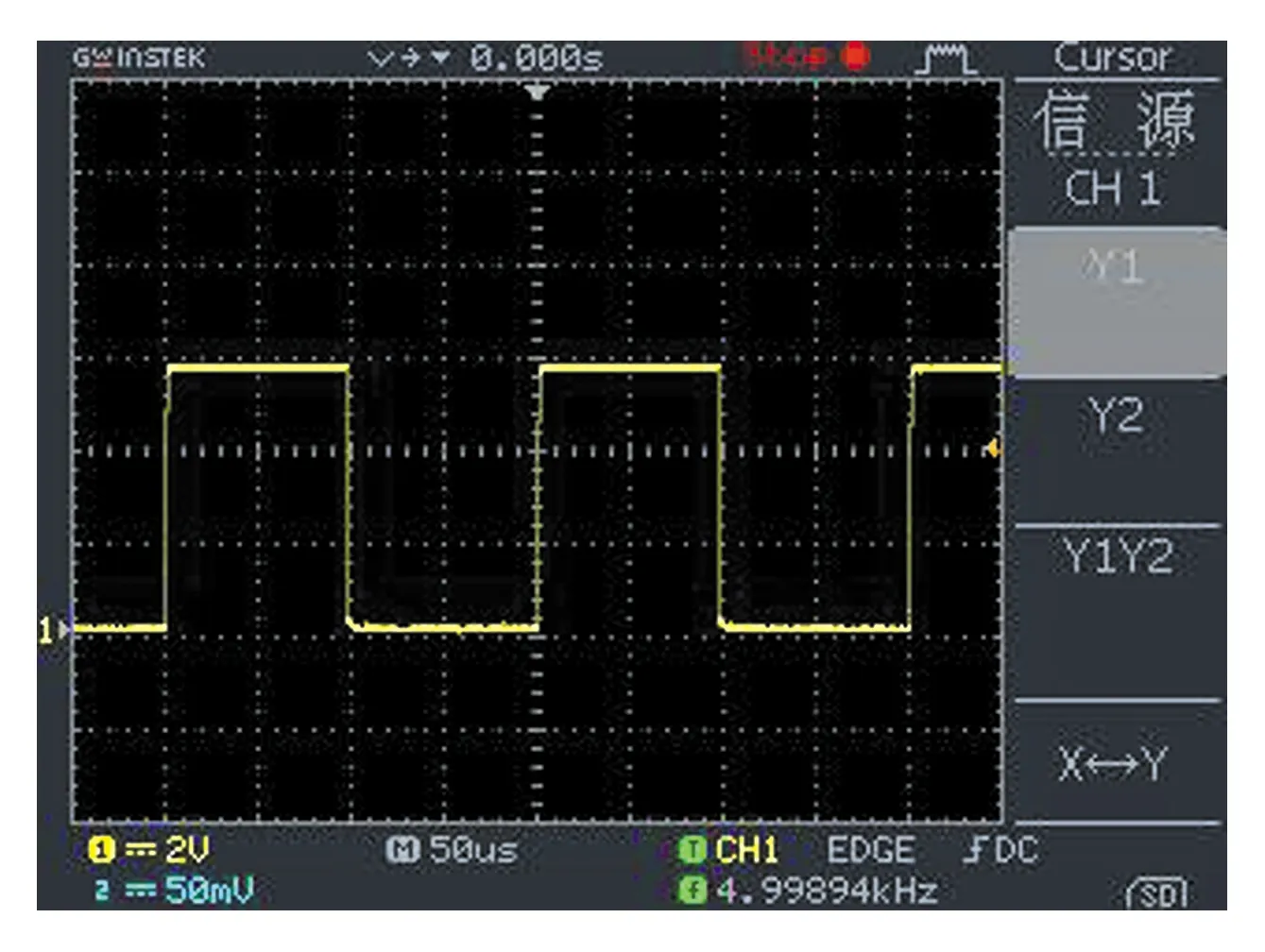
图7 实测时钟输出波形

图8 移位寄存器及控制电路

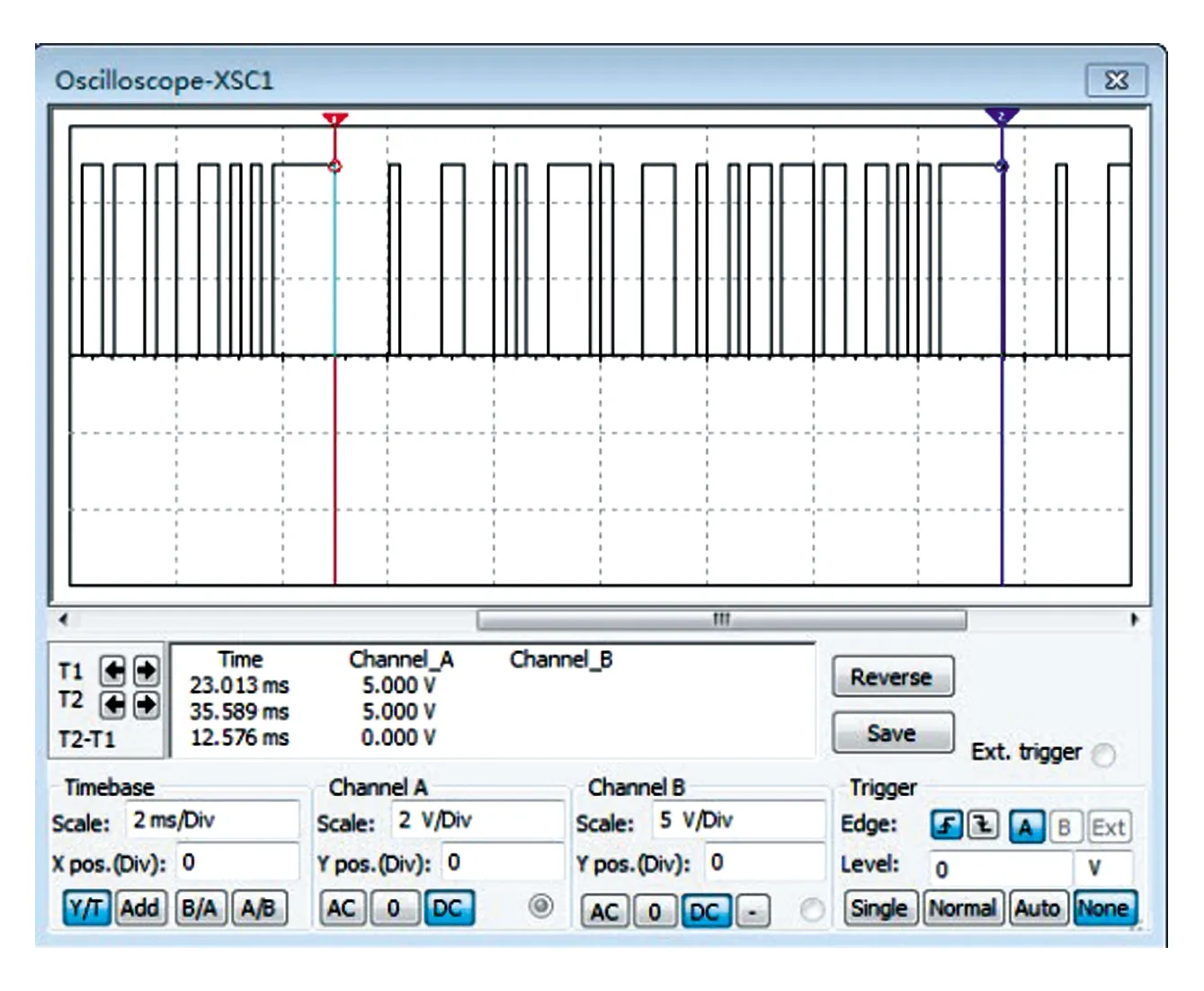
图9 仿真m序列信号波形

图10 实测m序列信号

输出的m序列信号高电平为+5 V,低电平为0 V,波形不具有幅度的对称性。为此增加了m序列变换电路,见图11,为线性电路。实验设定幅值为+1 V和-1 V,仿真波形见图12,实测波形见图13,与仿真设计的一致。

图11 m序列变换电路

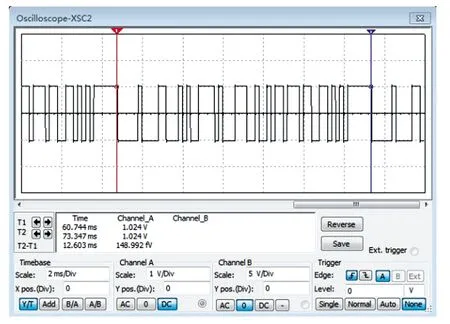
图12 仿真m序列变换后的波形

图13 实测m序列变换后的波形

2.2 信号激励及抬升电路

系统脉冲响应辨识需对激励信号及响应信号进行卷积运算,需利用单片机等数字处理器来完成[12]。由于激励信号及响应信号电平不在A/D采样要求范围内,需对2个信号进行抬升处理。激励信号的幅值为-1 V～+1 V,响应信号的幅值为-0.5 V～+0.88 V,利用分压电路和同相加法器将2个信号分别抬升1.45 V,满足电平0～3.3 V范围。图14为对应的电平抬升电路,电路由电阻串联分压电路、电压跟随器电路组成,抬升电路参考电压VR=5×4.1/14.1=1.454 V。抬升后m序列信号仿真电压范围+0.453 V～+2.453 V,硬件实测电压范围为+0.44 V～+2.40 V,电压范围略有变小,误差为2%。

图14 电压抬升电路原理图

变换后的m序列激励二阶系统的响应需能完全反映二阶系统的特性。图11输出的SSS信号端连接图1的SSS端。图15是仿真对应图1的Vos端输出波形及电平抬升后的波形,系统激励输出波形具有周期性,周期为12.6 ms,激励后二阶系统的输出电压幅值范围为-0.55 V～+0.77 V,利用图14电路波形抬升了1.45 V后,电压幅值为+0.9 V～+2.22 V。硬件实测激励后的波形幅值为-0.5 V～+0.8 V,抬升后的实测波形,电压幅值范围为+0.9 V～+2.28 V,满足设计预期。

图15 仿真激励输出抬升前、后的波形

2.3 辨识算法及实现

电平抬升后,利用STM32F103主机自带A/D模块对抬升后的激励信号和抬升后的系统输出电压进行两通道采样。在辨识算法嵌入式程序实现前,用Matlab软件进行了仿真设计,程序由5个自主编写和软件自带的其他函数组成,函数correlationAnalysis.m,函数transferFcn.m,函数estValue.m,函数ImpEstErr.m,函数theoreticalValue.m。

打开Matlab软件,在主窗口输入以下语句:

clear；% 清空工作空间的变量数据

clc； % 清除命令行的命令及多余的字符信息

然后打开correlationAnalysis.m函数,并在Matlab软件选单里点击“运行”控件,函数就开始运行,得到辨识均方误差和辨识结果比较曲线。给定的二阶系统,辨识结果与理论计算结果均方根最大误差为0.019 3；对应的辨识结果和理论计算值在一个周期内比较见图16；曲线非常接近,也验证了软件算法的有效性。

图16 理论计算和辨识算法结果对比

图17 系统软件流程图

图18为实测及结果显示,第一个波形为变换后的m序列,第二个波形为系统响应,黑色线为理论值,红色为辨识算法得到的响应曲线,辨识结果与理论只有一定的偏差,这跟实物电路元件参数与仿真的不一致有关,上位机数据处理得到最大偏差在2%以内。

图18 实测及结果显示

3 结论

一种二阶系统的脉冲响应辨识综合教学实验,包括m序列产生和脉冲响应测试2个子实验。m序列采用555定时器、D触发器、逻辑门、变换电路产生,涵盖了模拟电子技术和数字电子技术课程知识,没有采用可编程器件,不需复杂的编程和程序下载,增加了实验的适应性。采用6阶m序列信号,一方面考虑辨识的准确性,另一面兼顾了电路的复杂性。增加了m序列变换电路,提高了序列电平的对称性,扩大了序列的应用范围,同时将Multisim软件应用到教学实验设计中。采用了单片机自带A/D模块,不需增加硬件开销,稳定性好。采用了基于相关分析法来对脉冲响应曲线进行辨识,相比其他算法,电路可实现性强,并通过Matlab软件建模对算法进行验证。可扩展蓝牙模块,在上位机上显示输入、输出波形曲线及辨识曲线,方便直观,学生可以掌握上位机编程。

致谢:感谢中国高等教育学会及浙江天煌科技实业有限公司对实验设计的支持。

参考文献(References)

[1] 邓春龙,许伟明,张昕.相关函数脉冲响应法系统实时辨识[J].微计算机信息,2012,28(3):29-30.

[2] 于亮亮,宋汉文.环境激励下脉冲响应函数与相关函数的关系[J].噪声与振动控制,2017,33(3):14-18.

[3] 王燕平,陈昕志.利用相关分析法辨识系统脉冲响应[J].郑州工业高等专科学校学报,2003,19(2):1-2.

[4] 孙兴帅,秦琳琳,吴刚. 基于稀疏有限脉冲响应的温室温度系统建模[J].中国科学技术大学学报,2015,45(1):9-16.

1.4.1 心脑血管事件定义 心脑血管病事件定义为发生冠心病事件和（或）脑卒中事件。其中冠心病事件包括急性心肌梗死、冠心病猝死和其他冠心病死亡：脑卒中事件包括出血性脑卒中、缺血性脑卒中，但不包括一过性脑缺血和其他原因引起的脑血管病。在分析时，按冠心病事件和脑卒中事件进行统计分析，脑卒中事件再进一步划分为缺血性脑卒中事件和出血性脑卒中事件。同一类事件如发生2次或2次以上，以首次发生的事件为终点事件。

[5] 武欣,薛国强,底青云,等.伪随机编码源电磁响应的精细辨识[J].地球物理学报,2015,58(8):2792-2802.

[6] 高佳平,沈煜,陈鹏,等.用伪随机M 序列激励的绕组变形试验方法[J].中国电机工程学报,2016, 36(20):5678-5687.

[7] 方俊初,聂启燕.多次采样M序列法辨识LTI脉冲相应计算方法[J].河北工程大学学报,2016,33(3):109-112.

[8] 杨宪强.线性参数变化系统辨识方法研究[D]. 哈尔滨:哈尔滨工业大学,2014.

[9] 陈磊.连续系统的传递函数模型辨识[D].无锡:江南大学, 2012.

[10] 何华锋,李元凯,董海迪,等.伪随机信号(m序列)相关辨识的动态测试方法[J].中国测试,2013,39(4):88-92.

[11] 刘金琨,沈晓蓉,赵龙.系统辨识理论及Matlab仿真[M].北京:电子工业出版社,2013.

[12] 刘恒,吴朝阳,刘建成,等.一种典型闭环PID控制教学实验设计[J].实验技术与管理,2017,34(9):42-46.