一种改进的加权频差电阻抗成像算法

张夏婉

(南京邮电大学 自动化学院,江苏 南京 210000)

0 引言

电阻抗断层成像技术(Electrical Impedance Tomography, EIT)通过设置电极向人体施加安全的激励电流，同时在体表设置的电极处测量电压信号，经重构算法重构出人体某一块部位内部的阻抗或阻抗变化分布[1-4]。由于EIT技术对于检测疾病具有较好的无损伤性，大量的科研工作者投身到EIT的研究中，以期早日应用到临床应用当中，造福人类。EIT传统上可分为静态成像和动态成像。静态成像的数据采集系统要求苛刻，因此在临床应用中有一定的限制，目前仍在研究阶段。动态成像通过对不同时刻的测量数据进行差分成像，只可用于对某些疾病的发展过程进行实时图像监测，临床上对于病灶已形成并且在短时间内不会发生阻抗动态变化的疾病而言还不能实际应用。由于各种生物组织具有特定的电阻抗频谱特性[5-17]，不同频率点上的生物组织的电阻抗相差甚远。因此可利用不同频率下的测量数据进行差分成像，以期达到实时检测疾病的目的。这种成像方式即为准静态EIT成像(Quasi-Static EIT,QS-EIT)，是可以应用到临床应用当中的一种方法。近期，有人提出了基于加权频差阻尼最小二乘法的QS-EIT算法，有效地减少了背景区域存在伪影的问题[18]。

本文在基于加权频差阻尼最小二乘法的QS-EIT算法基础上提出对权值处理，从理论上对背景区域进行归一化，并且对先验信息矩阵进行改进，通过物理实验验证算法的有效性和可行性。

1 加权频差重构算法

1.1 数学模型

在成像区域Ω当中，当注入电流频率为ω时，在x∈Ω处的复电导率为:

γω(x)=σω(x)+iωεω(x)

(1)

其中σω(x)和εω(x)分别为电导率和电容率。

使用N电极多频EIT系统，电极设置在边界∂Ω上，可以将电极看作系统模型上面的一个点，依次在两个相邻电极上注入幅值为I、频率为ω的正弦激励电流。区域内电位和电导率的关系可由麦克斯韦方程组得出：

(2)

(在边界上)

(3)

设在区域Ω中，异常区域D在一个均匀电导率背景当中，有：

(4)

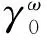
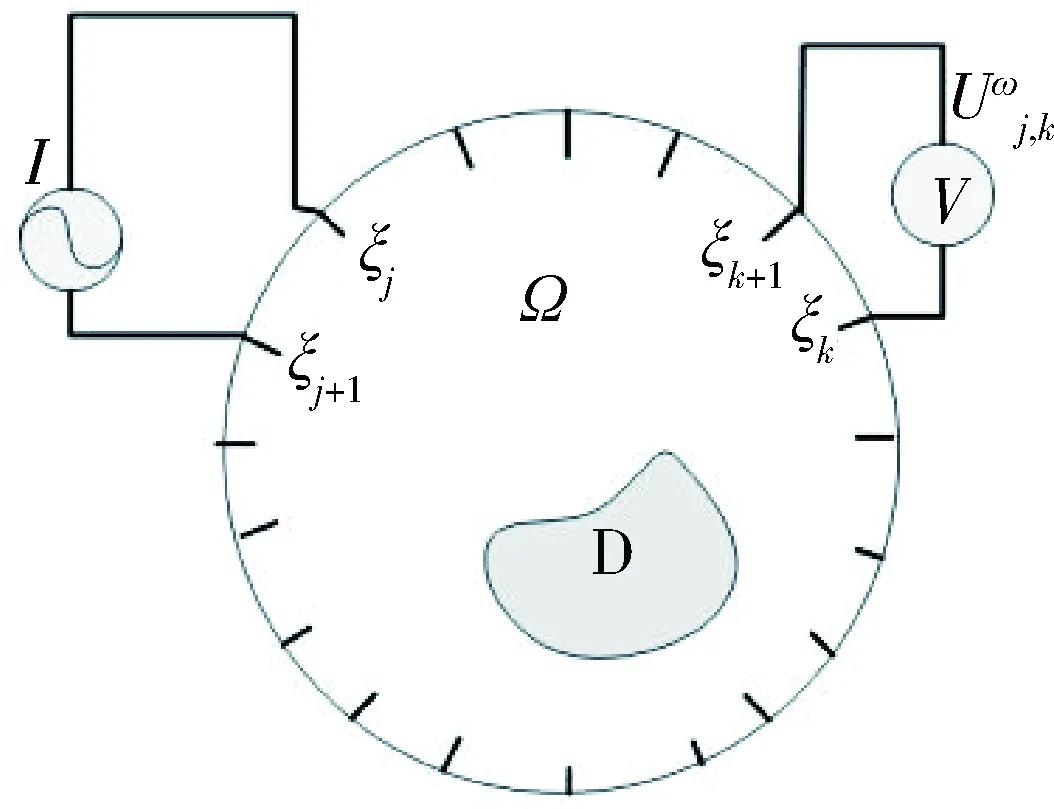
图1 EIT成像模型

分别测量电流频率为ω1和ω2时的电压数据集Uω1和Uω2。设加权频差数据矩阵V为：

(5)

从式(2)和式(4)可导出加权频差数据矩阵V和异常区域电导率的关系式：

(在区域内)

(6)

通过(3)式可以得到：

∂νυj|∂Ω=0 (在边界上)

(7)

从式(3)、格林公式和式(2)，可以得出[18]：

Vj,k=υj(ξk)-υj(ξk+1)

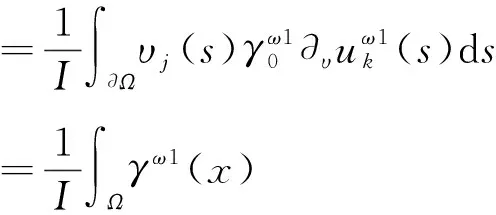
(8)

通过格林公式和式(6)、式(7)可以推导出:

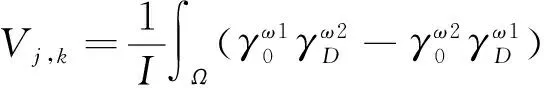
(9)

(10)

(11)

V=S·Δγ

(12)

式中，V为加权频差数据矩阵，Δγ为所要求的成像矩阵，S为敏感矩阵，矩阵元素为：

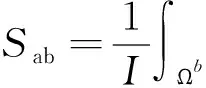
(13)

其中，Sab表示激励电流幅值为I时第a对激励-测量电极对对应的区域Ω当中的第b个单元所对应的敏感矩阵元素；和为阻抗分布为均匀分布时场域内的电位分布。

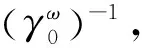
(14)

(15)

(16)

通过式(5)可以求得加权频差数据矩阵V。

1.2 传统加权频差方法

传统加权频差方法为：对于两组频率下的复电导率γω1和γω2，令γω2(x)为αγω2(x)，那么在复电导率差为Δγ=αγω2(x)-γω1时，对应的电压差矩阵为V=Uω2-αUω1。

改进后的加权频差方法，通过双加权的方法处理的背景区域电导率的值变为1，只通过异常区域电导率的变化进行成像，在理论上达到化背景区域电导率归一化的效果。

1.3 逆问题求解

对于病态方程V=SΔγ，利用最小二乘正则化方法对Δγ进行求解：

Δγ=(STS+λR)-1·STV

(17)

式中，λ为正则化参数，通过L曲线法选取[17]。本文中，对先验矩阵R进行改进。R是一个包含某些关于被测场域电导率分布的先验信息的调制矩阵，代表了各剖分单元间的互相关系，改进后的构造规则如下：假定有限元剖分单元数为H，则R为一个H×H的矩阵，其元素取值规则为：对每个单元进行编号后，如果两个单元拥有同一条三角边，则对应元素值为-1；如果单元有一条边在边界上，则其对应元素值为2；如果单元任一边都不在边界上，则其对应元素值为3。

1.4 传统先验矩阵

传统的先验信息矩阵R利用了敏感矩阵中的先验信息，具体实现为：

R=diag(STS)

(18)

敏感矩阵本身带有区域内部的先验信息，利用敏感矩阵数据作为先验信息虽然可以实现EIT成像，但是成像结果中存在较多伪影。本文直接将区域单元的位置作为先验信息，并通过物理实验进行验证比较两种方法的优越性。

2 实验结果

本实验采用课题组自主研发的MFEIT多频数据采集系统。实际测量中，激励频率选择5 kHz和10 kHz，激励电流为1 mA。物理模型内壁等间距地安放16个电极，对胡萝卜和黄瓜进行成像研究。

实验通过单目标和双目标两种模型进行物理实验比较，结果如图2～图5所示，发现改进后的加权频差EIT算法相比于传统加权频差成像算法明显地减少了很多伪影,成像效果更加清晰。

图2 单目标传统加权频差成像结果

图3 单目标改进加权频差成像结果

图4 双目标传统加权频差成像结果

图5 双目标改进加权频差成像结果

3 结论

本文对传统的加权频差EIT算法和改进后的加权频差EIT算法进行物理模型实验。从实验结果可以看出，改进后的加权频差EIT算法相比于传统加权频差成像算法减少了很多伪影。因此，该算法是一种有效的QS-EIT算法。

[1] GEDDES L A, BAKER L E. The specific resistance of biological material—a compendium of data for the biomedical engineer and physiologist[J]. Medical & Biological Engineering & Computing, 1967, 5(3):271-293.

[2] GABRIEL S, LAU R W, GABRIEL C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz[J]. Physics in Medicine & Biology, 1996, 41(11):2271-2293.

[3] GRIMNES S, MARTINSEN O G. Bioimpedance and bioelectricity basics (Third Edition)[M].Bioimpedance and Bioelectricity Basics. Elsevier LTD, Oxford, 2008.

[4] 何为,罗辞勇,徐征,等.EIT原理[M].北京：科学出版社，2009.

[5] 徐桂芝,李颖,杨硕,等.生物医学EIT技术[M].北京：机械工业出版社，2010.

[6] GRIFFITHS H, AHMED A. A dual-frequency applied potential tomography technique: computer simulations[J]. Clinical Physics & Physiological Measurement, 1987, 8 (S):103-107.

[7] GRIFFITHS H, LEUNG H T, WILLIAMS R J. Imaging the complex impedance of the thorax[J]. Clinical Physics & Physiological Measurement, 1992, 13 (S):77-81.

[8] JOSSINET J, TRILLAUD C. Imaging the complex impedance in electrical impedance tomography[J]. Chinical Physics and Physiological Measurement, 1992, 13 (S):47-50.

[9] RIU P J, ROSELL J, LOZANO A, et al. A broadband system for multifrequency static imaging in electrical impedance tomography.[J]. Clinical Physics & Physiological Measurement, 1992, 13 (A):61-65.

[10] SCAIFE J M, TOZER R C, FREESTON I L. Conductivity and permittivity images from an induced current electrical impedance tomography system[J]. Chinese Journal of Applied Physiology, 1994, 24(1):356-362.

[11] BROWN B H, BARBER D C, MORICE A H, et al. Cardiac and respiratory related electrical impedance changes in the human thorax[J]. IEEE Transactions on Biomedical Engineering, 1994, 41(8):729-734.

[12] BROWN B H, BARBER D C, WANG W, et al. Multi-frequency imaging and modelling of respiratory related electrical impedance changes[J]. Physiological Measurement, 1994, 15 (S):A1-12.

[13] SCHLAPPA J, ANNESE E, GRIFFITNS H. Systematic errors in multi-frequency EIT[J]. Physiological Measurement, 2000, 21(1):111-118.

[14] YERWORTH R J, BAYFORD R H, BROWN B, et al. Electrical impedance tomography spectroscopy (EITS) for human head imaging[J]. Physiological Measurement, 2003, 24(2):477-489.

[15] ROMSAUEROVA A, MCEWAN A, FABRIZI L, et al. Evaluation of the performance of the multifrequency electrical impedance tomography (MFEIT) intended for imaging acute stroke[C]// 13th International Conference on Electrical Bioimpedance and the 8th Conference on Electrical Impedance Tomography. Springer Berlin Heidelberg, 2007:275-286.

[16] XUETAO S, FUSHNEG Y, FENG F, et al. High precision multifrequency electrical impedance tomography system and preliminary imaging results on saline tank[C]//International Conference of the Engineering in Medicine & Biology Society. PubMed, 2005:1492-1495.

[17] SEO J K, LEE J, KIM S W, et al. Frequency-difference electrical impedance tomography (fdEIT): algorithm development and feasibility study[J]. Physiological Measurement, 2008, 29(8):929-944.

[18] 杨琳, 徐灿华, 付峰,等. 一种基于加权频差阻尼最小二乘的准静态EIT算法[J]. 仪器仪表学报, 2013, 34(8):1879-1885.