浅析数学思想方法在中考命题的渗透
2018-06-05江苏省徐州市第三十一中学蒋冬豹
江苏省徐州市第三十一中学 蒋冬豹
所谓数学思想方法,主要是指人们在研究数学过程中,对数学内容、方法、结构以及思维方式等的基本看法或者是数学本质的认识。初中学生是否能够具有自主学习能力,关键在于学生是否全面掌握了数学思想方法。究其原因在于数学思想方法的应用,有助于学生看清数学问题的本质,从而在解题过程中能够避免盲区,进而有效提升自身的解题能力。由此可见,初中数学教师进行数学思想方法教学的重要性。鉴于此,本文对“数学思想方法在中考命题的渗透”进行深入分析具有极为重要的现实意义。
一、方程思想分析
该思想主要是将数学问题当中的一些已知量与未知量之间的数学关系,转化为方程或者是方程组等数学模型,之后通过解方程或者是解方程组得出最终答案的方法便是方程思想。通常情况下,方程模型的建立主要是运用在代数、几何以及列方程(组)的应用题当中,相比其他方法,在上述类型应用题当中,方程思想方法的应用,更加有利于问题的解决。
例1(2017菏泽):某玩具厂生产一种玩具,按照控制固定成本降价促销,使生产的玩具能够及时促销,根据市场调查,每个玩具按照480价格销售,每天可售160,每降价1元,则可以多售出2只,问玩具销售价多少元时,便可以获取2万元的利润?
分析:学生在列方程解决此类型应用,有必要事先弄清题目中要求的量、等量关系等。之后明确未知数,通过等量关系建立起方程组。
解:设玩具售价为x元时,可获取2万元的利润,由题意可列方程(x-360)(160+2x(480-x)=20000,去分母整理得,x2-920+211600=0,解得x1=x2=460,答:玩具销售价460元时,便可以获取2万元的利润。
二、函数思想分析
在整个解题过程中,主要是通过未知数的设立,从而将一些变化的量,通过函数关系式加以表达,之后通过解决函数关系式得出相应的答案。值得注意的是在整个解题过程中,建立函数关系式可谓是重中之重。总而言之,函数思想就是通过函数概念、图象以及性质进行分析问题以及解决问题。
例2:某宾馆共有50个房间,房价为每天180元时,房间会住满。房价每天每增加10元时,将会出现一个空闲房间。宾馆对已有人居住的房间每天需要支出20元的杂费。根据相关规定,房价不得超过340元。设每个房间每天增加x元(x为10的整数倍)。(1)设宾馆一天的总利润为w元,求w与x的函数关系式;(2)宾馆一天需定租出多少个房间,产生最大利润?最大利润是多少元?
分析:本题主要考查的知识点是二次函数,在解题过程中,学生极易出现在求最值时不考虑x的范围,直接求顶点坐标这一错误。(1)房间订住后产生的利润是房价减去20元,总利润便是每间利润与所订的房间数的积;(2)先是求出二次函数的对称轴,根据二次函数的增减性以及x的范围便可以得出相应的答案。
解:(1)w=(180-20+x)(50-x/10),整理可得由此可得抛物线对称轴为x=170,并开口向下,当x<170时,w随x的增大而增大,但0≤x≤160,因而当x=160时,即房价是340元时,宾馆每天产生的利润最大化,房间数为34间,产生的最大利润为10880元。答:宾馆一天订住34个房间时利润最大,最大利润为10880元。
三、数形结合思想分析
所谓的数形结合思想,主要是指根据数学问题中的已知条件与结论之间的潜在关系,在分析代数意义的基础上,借助空间图形加以描述数量关系,促使其数量关系更为直观。在解题过程中,数形结合思想的应用能够快速找出解题出口,便于简化数学问题,从而有助于学生理解并解决数学问题。值得注意的是在数形结合思想的应用,要求学生极为熟悉概念、几何意义,同时要求学生具有数形转化能力。除此之外,在解决问题时,需要明确参数的取值范围。
例3:如下图,在壶内盛上一定量的水,壶下有小孔,水从小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用x表示时间,y表示壶底到水面的高度,下面的图象适合表示一小段时间内y与x的函数关系的是(不考虑水量变化对压力的影响)( )
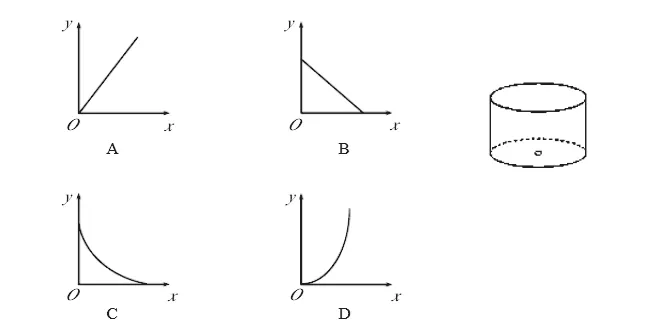
分析:本题主要考查的知识点便是函数与图象的应用,采取数形结合思想方法解决此类问题,首先需要明确的是在单位时间内流出的水是定量的,同时水将会随着时间的增加逐渐减少,为此正确答案应该选择B。
综上所述,近年来,中考试题当中明显侧重于数学思想方法的应用,尤其是数学压轴题,主要是考查学生是否能够应用数学思想方法解决问题。为此,初中数学教师在具体的教学过程中,有必要重视起数学思想方法的教学,并且通过典型例题,帮助学生掌握数个必要数学思想方法,以此促进学生数学素质的提升,从而有助于学生学习成绩的提高。
[1]陈安宁.浅谈数学思想方法对小学数学教学的启示——以鸡兔同笼问题为例[J].兰州文理学院学报(自然科学版),2014(06):97-100.
[2]施华玲.论小学数学教学中数学思想方法之渗透[J].福建教育学院学报,2014(06):68-70.
[3]王永春.小学数学教材与数学思想方法[J].课程.教材.教法,2015(09):44-48.
