深度学习视野下的初中数学课堂教学设计
——由“线段、射线、直线(第2课时)”教学设计引发的思考
2018-06-05江苏省太仓市实验中学赵红琴
江苏省太仓市实验中学 赵红琴
基于深度学习视野下的课堂教学设计,可以引发学生深层次地思考,更好地发展学生的思维,也会让数学课堂更具有活力。因此要让学生能达成深度学习,必须建立在教师深度备课后的教学设计的基础之上。下面就“线段、射线、直线(第2课时)”来阐述如何进行深度学习的教学设计。
本节课的教学目标是:能根据学习情境,借助于刻度尺、圆规等画图工具比较两条线段的大小;了解尺规作图,会画一条线段等于已知线段;理解线段的和、差表示;了解线段中点的含义;会求线段的长,进行简单的推理。
一、教学过程
1.引入新知
观察图片,提出问题:(如图1)如何比较两棵树的高低、两支笔的长短?

图1
【设计意图】通过目测法观察两棵树高,在比较两支笔的长短时,发现目测法不一定可靠,引出度量法与叠合法的必要。指出当我们把树、笔看成是一条线段时,我们可以把生活中的问题转化为几何问题,那么这就是两条线段的比较问题。教师创设真实的情境,激发出学生对学习活动的需求与真诚的热情,步入了课堂深度学习。
2.探索线段比较的方法
(1)在图1、图2上画线段AB、CD,隐去图片,如何对线段AB、CD进行比较?(2)对图1、图2进行几何画板度量验证;对图1、图2进行几何画板叠合法演示;(3)问题:将叠合后的图1旋转得图3,总结线段比较的结果及线段的和差表示。

图3
【设计意图】引导学生探索圆规的功能,通过实践操作,得出使用圆规可以把一条线段平移到另一条线段上。几何画板演示,让学生有了一个动态的叠合感受,帮助学生更好地理解叠合法。在叠合的图形中研究线段的和差数量关系,显得顺理成章。在操作、验证实践中加深对知识的深层次理解。
3.用尺规作一条线段等于已知线段
(1)尺规作图历史文化介绍 ;(2)探索用尺规作一条线段等于已知线段的方法;(3)教师示范,学生模仿,口述作法过程;(4)学生讨论探究如何用尺规作一条线段等于已知线段的2倍。
【设计意图】介绍尺规作图,增加数学史知识,激发兴趣,充满积极情感,营造支持深度学习的课堂文化。教师示范时,动作、顺序、作图语言要规范,给学生充分的时间模仿消化,操作时注意指导,也要发挥小组同伴间的互相帮助和示范作用。通过变式作图,提高学生应用新知识的能力,也为线段中点的得出做好准备。
4.揭示线段中点的概念
截取上面的作图部分,得图4:(1)归纳得出线段中点的定义;(2)用符号语言表示;(3)如AB=BC,则B是否一定是AC的中点?几何画板展示验证。
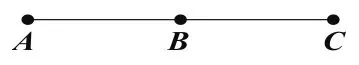
图4
【设计意图】引导学生读图,发现图中线段之间的数量关系,用文字语言表达线段中点的概念。同时,符号语言的表示让学生感受到几何语言的魅力,它是数形结合思想的最好体现,也是最简洁精彩的一种语言表达。最后,问题的提出引发学生深度思考,激发了学生思维的冲突,培养学生批判、创新、联想的能力,也让学生体会到数学概念的严谨性。
5.线段的计算
例题:已知线段AB=10cm。
(1)如图5,点C在线段AB上,且BC=4cm,D为AC的中点,求线段DB的长。
(2)点C在直线AB上,且BC=4cm,D为AC的中点,则线段DB=______。
(3)如图6,点C在线段AB上,且BC=4cm,D为AC的中点,E为BC的中点,求线段DE的长。
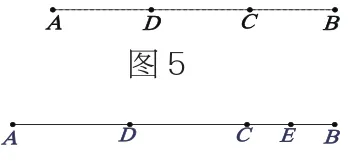
图6
(4)点C在直线AB上,D为AC的中点,E为BC的中点,DE=______。
【设计意图】本例题主要是对中点知识的应用。从一个中点到两个中点,从一个位置到不同位置,从BC已知到BC未知。层层递进,适合不同层次的学生,考查学生分析能力,简单推理,感受数形结合、分类讨论、整体思想以及方程思想等数学思想。梳理出与中点有关的基本图形、基本模型,让学生感受知识间的联系,变化之中的不变。经过变式的内容是有挑战性的,所以对内容的整合和变式是促成深度学习的有效途径。
6.学生编题
已知线段AB=10cm,____________,求_____。(请添加恰当条件,画出图形,提出问题)
【设计意图】添加条件编题,对本节课所学的知识进行了一次较高要求的迁移应用。开放性的问题设置,考查了学生的综合能力,发展了学生的思维,也可鼓励学生勇于创新、勇于尝试。
7.课堂小结
这节课学到了哪些知识?有哪些需要注意的地方?用到了哪些数学思想方法?
【设计意图】通过和学生一起深层次反思,让学生归纳总结自己的发现,感悟数学思想方法,构建自己的知识结构,体会几何的魅力以及成功的喜悦。
二、反思
1.教学内容要深度加工,构建知识间的关联
本节课程设计的学习过程:情景引入——探求新知——形成策略——知识应用——梳理总结。在每一个环节间都以有层次、有逻辑关联的问题来链接,驱动学生深层次思考,将各个模块内容串成线,思路清晰,自然展开。教师在教学设计时要精选例习题,通过一题多变、一题多解等使学生举一反三,构建问题间的联系,而不是一题一题孤立地呈现,让学生在比较之间分析、论证、归纳,把握问题本质,掌握数学思想方法。
2.学习情境要有真实性和批判性,走进学生情感和思维深处
学生的学习需要特定的课堂情境,本节课第二条线路是创设学生活动的情境,动脑、动手、动口、“动感”的过程,经历了尺规作图、几何语言叙述、感受几何画板、几何推理论证、编题等活动。在观察、猜想、验证的过程中,激发学生主动地、全身心地投入。
3.评价方式要即时有效,指明探究深化的方向
新课程标准倡导教师要关注学生的学习状态,指出了形成性评价在学生发展中的重要意义,但课堂上简单的赞扬等浅层评价常常出现,数学课堂教学评价需要的是有数学味的、有指导意义的即时性评价。
深度学习是以发展思维为任务的数学学习,任何没有思维含量,没有深度,不能引发学生兴趣的学习,都是难以提升学生的学习品质的。深度学习是一片广阔的领域,需要我们在教学实践中不断探索、提炼。
