一类完全三阶边值问题的上下解方法

李嫣红, 李永祥

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

讨论完全三阶非线性边值问题(BVP)

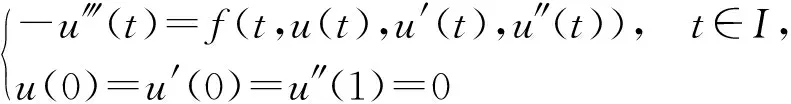
(1)

解的存在性与唯一性,其中f:I×R3→R连续,I=[0,1].

三阶常微分方程边值问题在应用数学和物理学等领域有着重要的应用[1-3],可用来描述电磁波、重力流、三层梁、地球引力吹积的涨潮以及带有固定或变化横截面的弯曲横梁的挠度等实际问题.近年来,人们通过相关问题的研究,得到了多种非线性分析的工具和方法,如打靶法[3]、拓扑度方法[4]、上下解方法[5]及单调迭代技巧[6]等.特别地,其解的存在性与唯一性受到了许多学者的关注[6-14].

文献[9-11]分别运用Krasnoselskii不动点定理、不动点指数理论和Leray-Schauder度理论,获得了(1)式非线性项不含导数项的简单三阶边值问题解的存在性结果;文献[13]运用锥拉伸与锥压缩型的Krasnoselskii不动点定理,获得了(1)式非线性项含一阶导数项问题解的存在性结果;对非线性项同时含一二阶导数项的一般情形,文献[6,14]分别运用单调迭代方法和Leray-Schauder非线性抉择讨论了解的存在性.但未见对更一般的三阶BVP(1)解的唯一性的研究.

鉴于上述文献中所提到的方法都不能处理二阶导数项问题.受文献[15]的启发,给出解的二阶导数的有界估计,并对BVP(1)解的存在性与唯一性做讨论.本文在提出一个恰当的Nagumo条件来限制f关于z增长的情形下,运用一个特殊的截断技巧、Leray-Schauder不动点定理及上下解方法,获得BVP(1)解的存在性,并在解存在的基础上,借助微分中值定理,获得了BVP(1)解的唯一性.

为了叙述方便,需引入以下条件.

(H1) 存在[0,+∞)上的正值连续函数h(ρ)满足

(2)

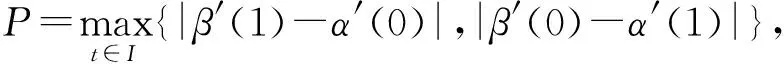
|f(t,x,y,z)|≤h(|z|),t∈I,α(t)≤x≤β(t),
α′(t)≤y≤β′(t),z∈R;

(3)

(H2) 当α(t)≤x≤β(t),(t,y,z)∈I×R2时,

f(t,α(t),y,z)≤f(t,x,y,z)≤f(t,β(t),y,z),

∀t∈I;

(H3) 对∀(t,x,y,z)∈I×R3,有

fx(t,x,y,z)+fy(t,x,y,z)<0.

(4)

本文的主要结果如下.

定理1.1设f:I×R3→R连续.BVP(1)存在下解α(t)及上解β(t),满足α′(t)≤β′(t).若f满足条件(H1)和(H2),则BVP(1)至少存在一个解u(t)∈C3(I),满足

α(t)≤u(t)≤β(t),

α′(t)≤u′(t)≤β′(t).

定理1.2设f:I×R3→R连续.α(t)、β(t)分别是BVP(1)的下解和上解.若f在I×R3上关于变量t、x、y、z连续可微,且满足条件(H1)～(H3),则BVP(1)有唯一解u(t)∈C3(I),满足

α(t)≤u(t)≤β(t),

α′(t)≤u′(t)≤β′(t).

1 准备工作

定义1设α(t)∈C3(I),若α(t)满足

(5)

则称α(t)为BVP(1)的下解.若(5)式均取反向,则称α(t)为上解.

对∀h∈C(I),BVP(1)相应的线性边值问题(LBVP)

(6)

存在唯一解u∈C3(I),即

(7)

其中

(8)

为相应的Green函数,则解算子S:C(I)→C3(I)为线性有界算子.由嵌入C3(I)→C2(I)的紧性,则S:C(I)→C2(I)是线性全连续算子.

为完成定理1.1的证明,需要下列解集的‖·‖C估计.

证明对∀t∈I,有

因此

引理1.2设f:I×R3→R连续.若存在常数a,b,c,d≥0,满足a+b+c<1及d>0,使得f满足条件:

1) |f(t,x,y,z)|≤a|x|+b|y|+c|z|+d,t∈I,x,y,z∈R;

2) |f(t,x2,y2,z2)-f(t,x1,y1,z1)|≤a|x2-x1|+b|y2-y1|+c|z2-z1|,t∈I,x2,x1,y2,y1,z2,z1∈R,

则BVP(1)存在唯一解.

证明存在性 设f:I×R3→R连续.对∀u∈C2(I),令

F(u(t))=f(t,u(t),u′(t),u″(t)),t∈I,

(9)

则F:C2(I)→C(I)连续,把有界集映为有界集.定义映射A:C2(I)→C2(I),

A=S∘F.

由S:C(I)→C2(I)的全连续性,A:C2(I)→C2(I)为全连续映射.按S的定义,BVP(1)的解等价于A的不动点.对A应用Leray-Schauder不动点定理.考虑方程簇

u=λAu, 0<λ<1.

(10)

下证方程(10)的解集在C2(I)中有界[16].

设u∈C3(I)为某个λ∈(0,1)相应的方程(10)的解,则u=λAu=S(λF(u)).按S的定义,u为h=λ(F(u))相应的LBVP(6)的解,因此u∈C3(I)满足

(11)

由条件1),有

|u‴(t)|≤λ|f(t,u(t),u′(t),u″(t))|≤
a|u(t)|+b|u′(t)|+c|u″(t)|+d,

方程两边取‖·‖C,由引理1.1,有

因为

唯一性 设u1,u2∈C3(I)为BVP(1)的解.令u=u2-u1,则由方程(1),有

因u∈C3(I)为h(t)相应的LBVP(6)的解,由条件2)及引理1.1有

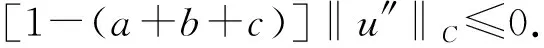
则u≡0,即u1=u2,因此,BVP(1)有唯一解.

2 主要结果的证明

定理1.1的证明由条件(H1),∃M>0,使得

(12)

取常数N=M+‖β‖C2+‖α‖C2+1,令

(13)

(14)

(15)

作f(t,x,y,z)的截断函数

(16)

有

|f*(t,x,y,z)|≤

‖α‖C+‖β‖C,|y|≤

则f*:I×R3→R连续有界.因此,由引理1.2,修改了的边值问题

(17)

有解u0(t)∈C3(I),下证u0(t)为BVP(1)的解.

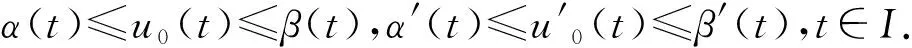
1) 若t0∈(0,1),则u″(t0)=0,u‴(t0)≤0,即

u‴0(t0)≤β‴(t0).

(18)

根据截断函数的定义,条件(H2)及(18)式有

f(t0,η1(t0,u0(t0)),β′(t0),[β″(t0)]N)-

f(t0,β(t0),β′(t0),β″(t0))-

f(t0,β(t0),β′(t0),β″(t0))≤-β‴(t0),

即u‴0(t0)>β‴(t0),与(18)式后一不等式矛盾!故t0∉(0,1).

2) 若t0=0,则

(19)

3) 若t0=1,则u″(1)=u″(1-)≥0,即

(20)

又

由P的定义及中值定理,则存在t0∈(0,1),使得

下证情形1),其他情形类似可证.当1)成立时,根据上述证明及条件(H1),有

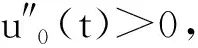
(21)

即

与(12)式矛盾! 故

综上所得,f*=f,即u0(t)为BVP(1)的解.

定理1.2的证明由定理1.1,BVP(1)至少存在一解,下证唯一性.

设u1、u2∈C3(I)都为BVP(1)的解,记u(t)=u1(t)-u2(t).由微分中值定理,u(t)∈C3(I)为方程

(22)

u″(t*)=0,u‴(t*)≤0,

(23)

(24)

由a(t*)≥0,(24)及(4)式,有

-u‴(t*)=a(t*)u(t*)+b(t*)u′(t*)+
c(t*)u″(t*)=

a(t*)u(t*)+Kb(t*)≤

a(t*)|u(t*)|+Kb(t*)≤

K(a(t*)+b(t*))<0,

由

即u≡0,因此BVP(1)有唯一解.

[1]GREGUS M. Two sorts of boundary value problem of nonlinear third order differential equations[J]. Arch Math,1994,30(4):285-292.

[2]BERNIS F, PELETIER L A. Two problems from draining flows involving third-order ordinary differential equations[J]. SIAM J Math Anal,1996,27(2):515-527.

[3]TROY W C. Solutions of third-order differential equations relevant to draining and coating flows[J]. SIAM J Math Anal,1993,24(1):155-171.

[4]O′REGAN D. Topological transversality:applications to third order boundary value problems[J]. SIAM J Math Anal,1987,18(3):630-641.

[5]CABADA A. The method of lower and upper solutions for second,third,fourth and higher order boundary value problems[J]. J Math Anal Appl,1994,185(2):302-320.

[6]姚庆六. 一类非线性三阶两点边值问题的单调迭代方法[J]. 云南大学学报(自然科学版),2011,33(1):1-5.

[7]YAO Q L, FENG Y Q. The existence of solution for a third-order two-point boundary value problem[J]. Appl Math Lett,2002,15(2):227-232.

[8]冯育强,刘三阳,姚庆六. 关于三阶边值问题解的存在性[J]. 应用数学,2003,16(3):108-111.

[9]姚庆六. 三阶常微分方程的某些非线性特征值问题的正解[J]. 数学物理学报,2003,A23(5):513-519.

[10]张琦. 一类三阶两点边值问题的变号解[J]. 数学物理学报,2013,A33(2):216-223.

[11]刘瑞宽. 一类奇异三阶两点边值正解的存在性[J]. 四川师范大学学报(自然科学版),2014,37(4):482-486.

[12]白婧,李永祥. 含一阶导数项的三阶周期边值问题解的存在唯一性[J]. 四川师范大学学报(自然科学版),2015,38(6):834-837.

[13]姚庆六. 一类奇异三阶常微分方程的正解存在性与多解性[J]. 华东师范大学学报(自然科学版),2010,2010(3):113-118.

[14]姚庆六. 线性增长限制下一类三阶边值问题的可解性[J]. 纯粹数学与应用数学,2005,21(2):164-167.

[15]BAI Z B. The upper and lower solution method for some fourth-order boundary value problems[J]. Nonlinear Anal,2007,67(6):1704-1709.

[16]DEIMLING K. Nonlinear Functional Analysis[M]. New York:Springer-Verlag,1985.