GNSS诱偏系统转发器的布阵高度分析
2018-06-04陈树新刘卓崴
黄 森,陈树新,刘卓崴,陈 坤
(空军工程大学 信息与导航学院,西安 710077)
0 引 言
全球导航卫星系统(global navigation satellite system,GNSS)系统已成为火力打击武器和无人侦察机的重要组成部分,为保护重要设施和区域不被侦查打击,针对卫星导航的干扰措施应运而生[1]。相对于传统压制干扰无法控制干扰对象运动轨迹的不足,GNSS诱偏系统在要地上空部署转发平台,利用转发卫星信号,改变信号的传播路径和时间,使干扰对象偏离到目标点以外的安全区域[2]。
通过设定转发器的布阵位置和信号转发时延值[3-4],该系统可将目标接收机从真实点欺骗至一虚假位置,构成映射关系,而真实点的邻域也会连续地映射到虚假点的邻域。为了避免映射邻域中位置的异常变化被完好性监测所识别,文献[5]对邻域映射的保形性进行研究,并定义了比例因子K作为衡量指标。在此基础上文献[5-6]相继研究了转发器布阵位置与虚假点的位置对映射邻域保形性的影响,文献[7]更是得出转发器位于卫星与真实点连线的等比例处时,2个邻域会近似“等比例”的结论。
上述的文献未对转发器布阵高度进行影响分析,且均只分析了真实点在初始位置的领域映射情况,未考虑由于目标的高动态性,真实点远离初始位置所引起的映射性能显著恶化。本文通过解析分析,得到了布阵高度对映射性能的影响,并给出了布阵的准则,减小了映射误差偏差。
1 转发诱偏系统模型
转发诱偏系统是通过改变信号在空间中的传播时间,对接收机进行诱导欺骗。该系统由转发器、运载平台和地面控制站3部分组成。运载平台搭载转发器部署在空间中,控制站监测目标的运动状态并发送指令给转发器,转发器根据指令对卫星信号进行不同的延时转发,其模型如图1所示。
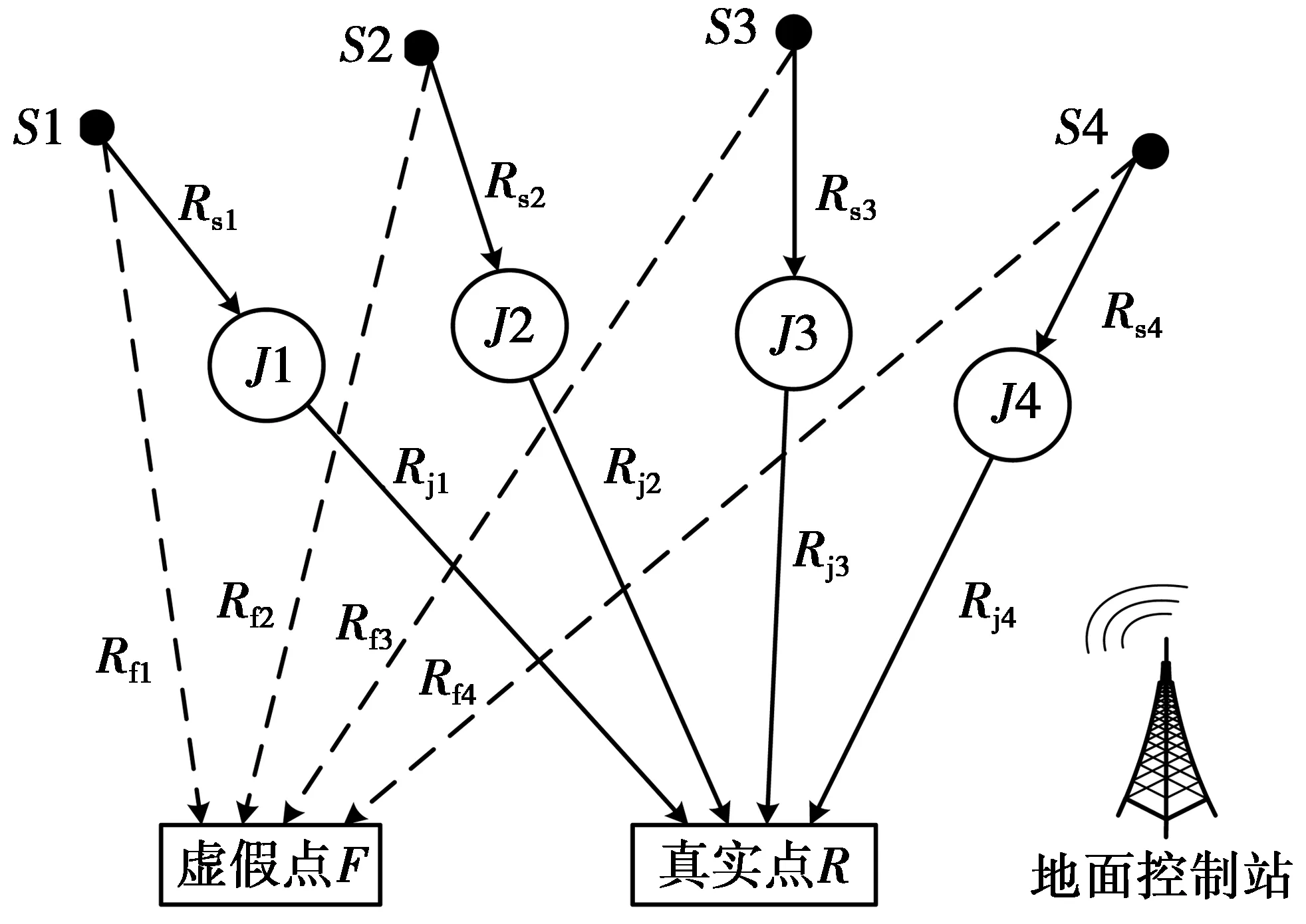
图1 GNSS转发诱偏系统原理示意图Fig.1 Schematic diagram of GNSS decoying system
图1中,Si为在该区域中备用作导航定位的卫星,i=1,2,3,4;Ji为在空中的转发平台,可以是飞机、气球、飞艇等,其核心是射频接收转发器,将卫星信号接收之后,加入一定时延再发射出去,i=1,2,3,4;R是目标接收机所在的真实点;F是目标接收机被转发诱偏后错误定位到的虚假点;Rsi,Rji,Rfi分别表示卫星到转发器,转发器到真实点和卫星到虚假点的距离,i=1,2,3,4。另外,设Rri表示卫星到真实点的距离,i=1,2,3,4。
GNSS系统采用“伪距”来定位,其基本原理是同时接收4颗(或4颗以上)卫星信号,并测量其到达接收机的时间差,计算出卫星与接收机的距离。由于时间差或距离测量值有误差,因此,称之为伪距。利用三球交汇原理,联立方程见(1)式,求解位置。
ρi=[(xi-x)2+(yi-y)2+
(zi-z)2]1/2+c·tR
(1)
(1)式中:ρi为各卫星信号的传播伪距;tR是用户钟和卫星钟之间的钟差;c为光速;(xi,yi,zi)是各卫星在地心地固坐标系(earth centered earth fixed,ECEF)中的坐标;(x,y,z)是接收机的坐标。(1)式中(x,y,z)和tR均为待求解量。
在不受诱偏的情况下,导航信号的传播路径为从卫星到接收机,即ρi=Rri。而当有GNSS诱偏导航装置的情况时,接收到的导航信号则是需经转发器延时Δτi秒的转发信号,因此,传播路径和时间差发生改变,即
(2)
在实际应用中,为防止接收机自身的完好性监测产生告警,虚假点一般选择在真实点附近。因此求解点F时,可将真实点R(xr,yr,zr,tR)视为其近似解,即
F=R+ΔX
(3)
(3)式中,F,R分别包含有点F,R位置信息和钟差信息的向量形式:
将(2)式代入(1)式中,并将各非线性方程在R处按泰勒级数展开,忽略高阶项,化简整理成矩阵形式
A+M·ΔX=T
(4)
(4)式中:
2 区域映射模型及优化分析
2.1 区域映射模型
诱偏系统受限于系统实时性差,采用固定转发器和固定时延进行工作。为避免转发信号产生的位置信息被接收机自主完好性监测[8-9],系统应实现高保形性的连续诱偏,因此,需对目标真实点与虚假点邻域的映射情况进行分析。
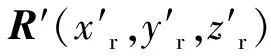
(5)
其中,邻域的半径应小于某一小值a,即
(6)
GNSS接收机监测可通过识别位置参数的不合理变化来剔除不可信数据,因此,为了提高诱偏系统的可行性,可对邻域映射的保形性进行分析,即对目标在2个邻域中位置参数的变化一致性进行分析。根据(3)式,可将点F与点R的变化程度的差异值用各自位移的空间距离‖ΔX′-ΔX‖2来衡量,‖ΔX′-ΔX‖2越小,2个邻域中位置参数变化越一致,越不易被完好性检测识别。
从(4)式中可以看出,‖ΔX′-ΔX‖2的值与矩阵A和M有关,而其中与诱偏系统参数有关的则是转发器Ji的位置。文献[7,10]认为在布阵时,转发器Ji位于卫星Si与接收机初始位置R连线上,且满足(7)式时,区域映射的保形性较好,如图2所示。图2中,R′点表示目标是运动离开R点后的位置,dR为目标的位移。
(7)

图2 卫星、转发器和接收机的空间关系Fig.2 Spatial relations among satellite, repeater and receiver
(7)式代入(4)式后是一个关于dR和λ的矩阵函数,但由于是对转发器布阵的分析,所以,可将dR视为一个定值,将邻域映射保形性研究转变成一个关于λ的目标函数‖ΔX′-ΔX‖2最小化问题的研究,即
min ‖ΔX′-ΔX‖2
s.t. ΔX′(λ)=M-1·[T-A(λ)]
(8)
2.2 区域映射优化分析

min ‖ΔX′-ΔX‖2⟺
(9)

min ‖M-1·[T-A(λ)]‖2⟺
min ‖T-A(λ)‖2
(10)
一方面,系统为满足转发时延是可实现的,必须保证各时延值大于或等于零,即T≥0;另一方面,根据三角形定理,图2中各线段满足Rri-Rsi-Rji≤0,即A(λ)≤0。因此,(10)式中矩阵范数的最小化可以等价为矩阵A(λ)中各负值元素的最大化:
min ‖A(λ)‖2⟺
max (Rri-Rsi-Rji)
(11)
设L=Rri-Rsi-Rji,(11)式中:
求L关于λ的导数
(12)
(12)式中:
P(λ)= [λ·(xi-xr)-dxr]·(xi-xr)+
[λ·(yi-yr)-dyr]·(yi-yr)+
[λ·(zi-zr)-dzr]·(zi-zr)
Q(λ)={[λ·(xi-xr)-dxr]2+
[λ·(yi-yr)-dyr]2+
[λ·(zi-zr)-dzr]2}1/2
由(7)式可知,0<λ<1,且相较与卫星的距离,目标在地球表面的移动距离(dxr,dyr,dzr)很小,所以,只要转发器的部署高度不在卫星轨道上,均可满足
此时,(12)式经放缩法推导可得
(13)
λ的取值区间为
(14)
此时,‖ΔX′-ΔX‖2为一个关于λ的单调减函数。
通过解析分析可得结论,在转发器布阵满足(14)式的情况下,λ的值越大,‖ΔX′-ΔX‖2目标函数的值越小,目标接收机在2个邻域中的位置参数变化趋势越一致,映射偏差越小。若将转发器视作伪卫星星座,其布阵高度越高意味着星座多面体体积越大、GDOP越小,可见这种布阵高度优化也符合传统的选星准则[11]。
3 仿真分析
在卫星、转发器、目标接收机的空间位置关系来看,上面分析中的λ值可看作是转发器的离地高度的另一表现形式。因此,仿真实验可采用转发器部署的海拔高度来对结论进行验证。
仿真中,初始设置时卫星、真实点和虚假点的位置数据来自文献[13]采用的实测数据,其在ECEF坐标系下的位置如表1所示。
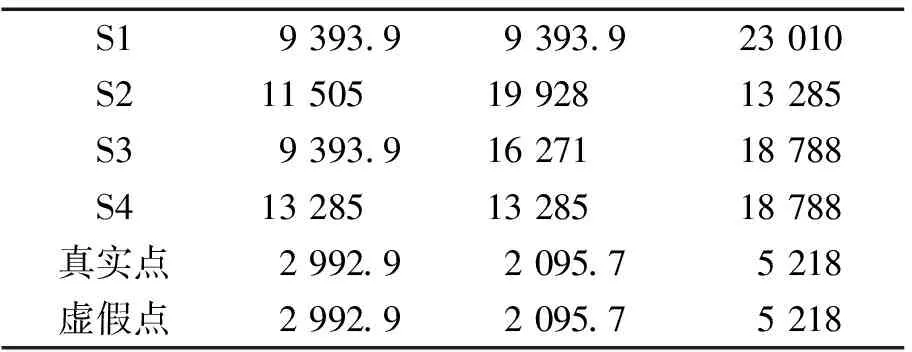
表1 卫星、真实点和虚假点位置坐标
针对本文分析得到结果,采用转发器J1的离地高度h作为控制量,对转发平台进行布阵。由于固定转发器一般都部署在临近空间(20~80 km),因此,仿真中取h=20,40,60 km作为典型值,其对应的λ值分别为6.883 8×10-4,1.688 7×10-3,2.689 0×10-3,此时各转发器的坐标分别为
(15)
3.1 仿真一:运动轨迹的映射情况
假设转发器初始布阵完毕并转发信号实施干扰,此时目标真实点继续运动,对该运动取200个采样点,采样间隔为1 s,采样点的轨迹为

(16)
其在不同布阵高度h下映射的虚假点轨迹和真实点轨迹如图3所示。
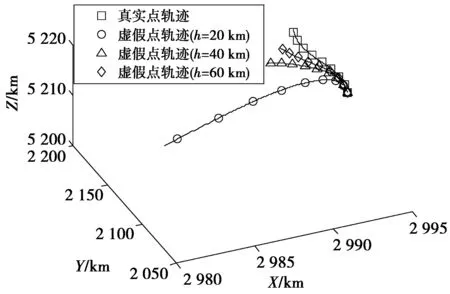
图3 接收机运动轨迹映射情况Fig.3 Mapping of receiver trajectory
图3中,真实点和虚假点运动轨迹的水平位移变化偏差‖ΔX′-ΔX‖2如图4所示。
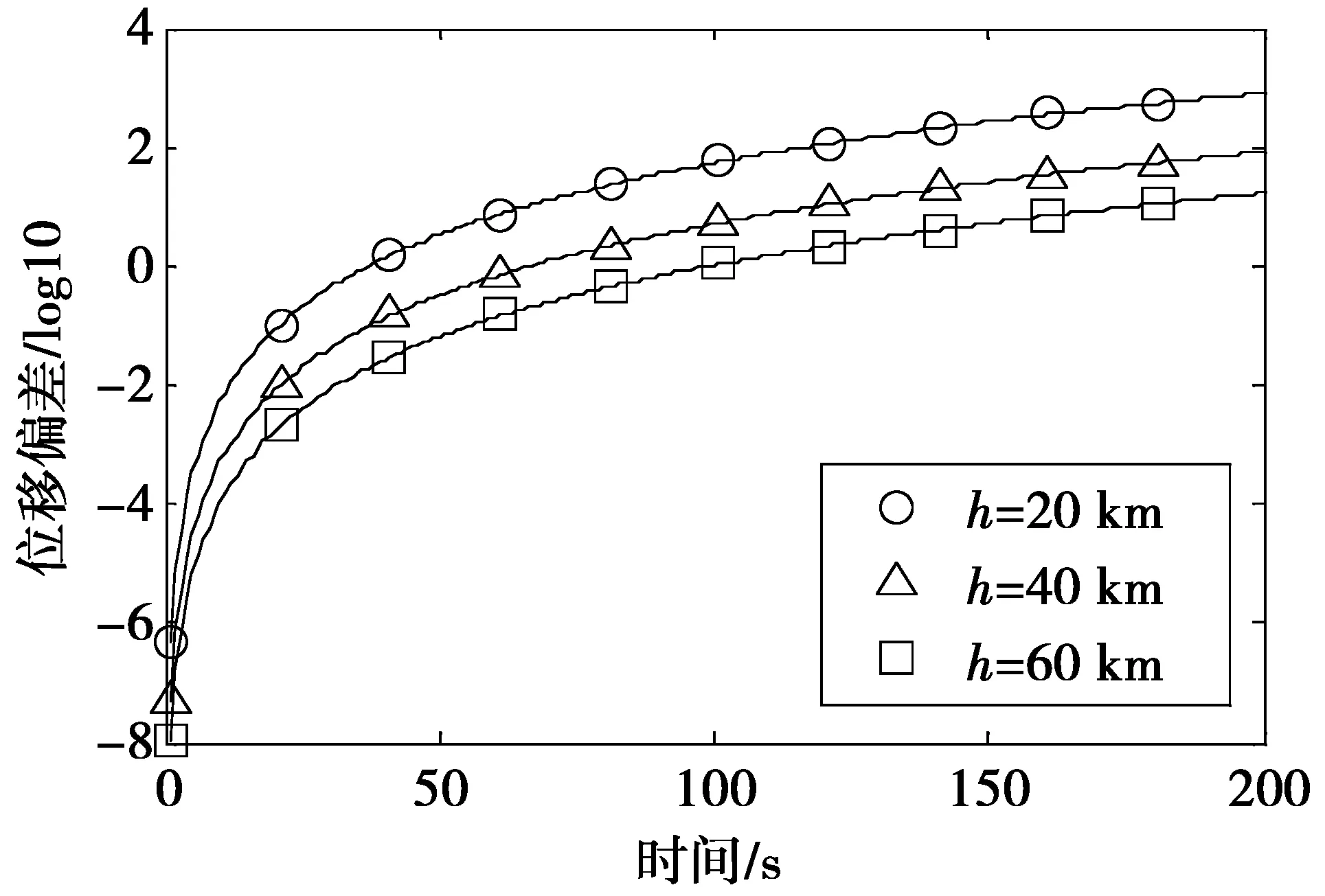
图4 真实点和虚假点位移变化偏差量Fig.4 Displacement variation between false and actual position
通过仿真可以得到以下结论。
1)当目标接收机逐渐远离初始位置R时,虚假点的运动轨迹逐渐远离真实点的运动轨迹,且当h值越小时,轨迹偏差越明显;当h值越大时,虚假点的映射轨迹越接近真实轨迹。
2)在相同运动轨迹下,目标接收机虚假点与真实点的位移变化偏差量与转发器布阵有关,当h值越小时,这种偏差量越大。
3.2 仿真二:真实点邻域映射情况
仿真一中的轨迹偏差是对位置参数变化一致性的长时描述,而领域映射情况则是瞬时描述。当采样点t=100时,将球心在真实点R′、半径为d=10 km的球作为该采样时刻真实点R′的邻域,如图5所示。在仿真一的条件下,对同一真实点R′的领域在不同典型布阵高度h下的映射虚假点F′的邻域进行了仿真,如图6、图7所示。其中,虚假点邻域与真实点邻域在形状上越相似,尺度上越接近,说明映射的保形性越好。
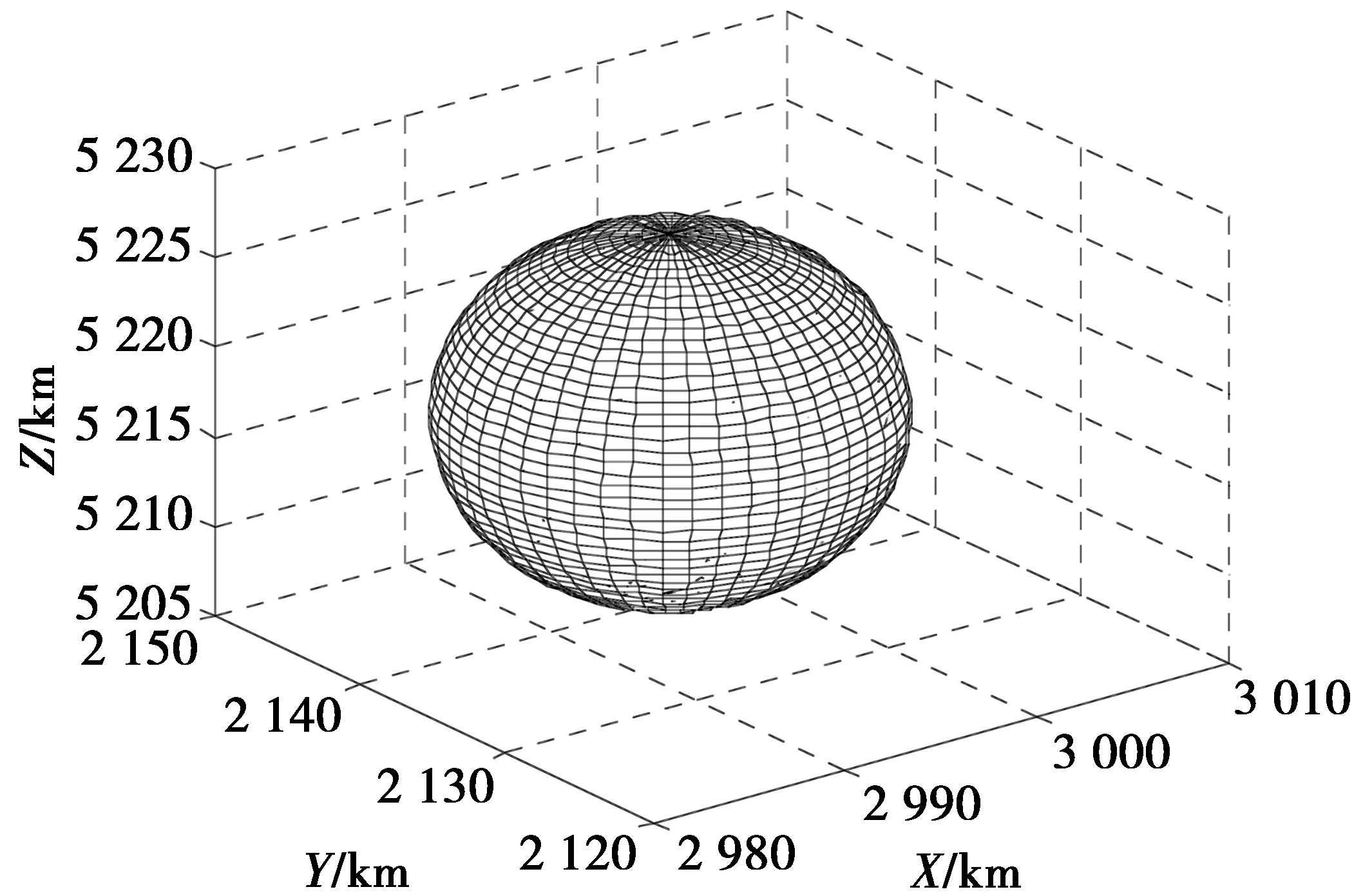
图5 真实点邻域Fig.5 Neighborhood of actual position

图6 h=20 km时虚假点的邻域Fig.6 Neighborhood of false position when h is 20 km
其中,离地h=20 km的情况下映射邻域形状产生较大形变,离地h=60 km的情况下映射邻域与真实领域形状相似,但有尺度上的不同。此处利用映射比例因子K来对不同映射邻域的保形性进行定量描述[5],如(17)式所示,即真实点与虚假点的邻域半径之比的最大值Kmax和最小值Kmin越接近1,映射效果越好,比例因子与转发器部署高度h的关系如图8所示。
(17)

图7 h=60 km时虚假点的领域Fig.7 Neighborhood of false position when h is 60 km

图8 比例因子与转发器高度关系Fig.8 Scaling factor versus to the altitude of receivers
仿真一中3种典型布阵情况下的比例因子如表2所示。
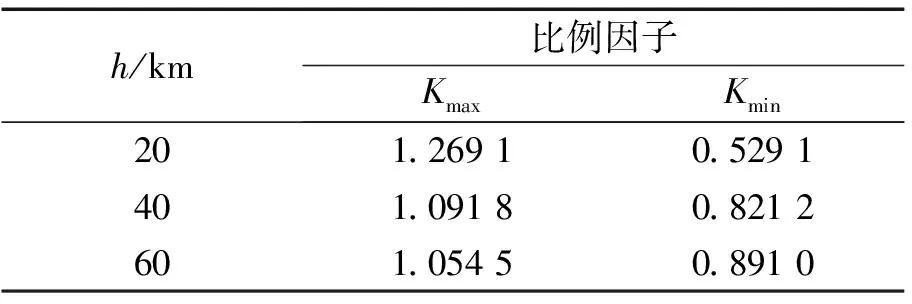
表2 比例因子典型值
通过仿真可以得到结论。
1)在目标接收机经运动后位于R′处时,邻域的形状经映射后会产生形变,转发器布阵高度h越大,Kmax,Kmin越接近1,两邻域形状越相似。
2)在临近空间内,不论转发器布阵高度h如何选择,其邻域形变永远存在,无法达到一致。
4 结束语
本文根据GNSS多站转发诱偏系统原理,在转发时延值和转发器位置更新实时性差的应用背景下,分析了转发器布阵高度对系统映射性能的影响,得到了升高其布阵高度以优化映射性能的结论。此外,仿真结果表明:在临近空间内,该系统的映射邻域存在无法避免的形变,因此,为应对接收机自主完好性监测的识别,该系统必须解决实时性的问题。本文的结论为GNSS诱偏系统转发器的布阵提供理论依据。
参考文献:
[1] PSIAKI M L,HUMPHREYS T E.GNSS Spoofing and Detection[J].Proceedings of the IEEE,2016,104(6):1-13.
[2] 杨景曙,曾芳玲,盛琥,等.通过区域映射实现诱导的GPS干扰系统[J].电子学报,2005,33(6):1036-1038.
YANG Jingshu,ZENG Fangling,SHENG hu,et al.A Jamming System Through Section Mapping for GPS Navigation[J].Acta Electronica Sinica,2005,33(6):1036-1038.
[3] 张颂,杨景曙,潘高峰,等.诱骗暨导航一体化系统中诱偏时延算法[J].安徽大学学报:自然科学版,2011,35(1):64-68.
ZHANG Song, YANG Jingshu, PAN Gaofeng, et al. The time-delay algorithmic in GPS area-mapping deceiving unites battlefield navigation integrative system[J]. Journal of Anhui University: Natural Science Edition, 2011, 35(1):64-68.
[4] 史密,陈树新,刘卓崴.GPS转发式欺骗时延分析与优化[J].重庆邮电大学学报:自然科学版,2017,29(1):56-61.
SHI Mi, CHEN Shuxin, LIU Zhuowei. Analysis and optimizing of time-delay in GPS repeater deception[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2017, 29(1) :56-61.
[5] 田东生,曾芳玲,杨景曙.对GPS区域映射比例影响因素的分析[J].现代防御技术,2008,36(5):52-56.
TIAN Dongsheng, ZENG Fangling, YANG Jingshu. Influence factor analyzing for GPS area mapping scale[J]. Modern Defence Technology, 2008,36(5):52-56.
[6] 张颂,苗苗,侯帅,等.多站与单站转发实现GPS诱导的性能研究[J].现代雷达,2013,35(1):1-5.
ZHANG Song, MIAO Miao, HOU Shuai, et al. A Study on the Performance Between Multi-transmitters and Single Transmitter GPS Inducing System[J]. Modern Radar, 2013,35(1):1-5.
[7] 闫占杰,吴德伟,何晶,等.GPS转发欺骗式干扰源部署方法[J].现代雷达,2015,37(3):75-79.
YAN Zhanjie, WU Dewei, HE Jing, et al. Deployment Method of Jammer in GPS Repeater Deception Jamming[J]. Mordern Radar, 2015,37(3):75-79.
[8] 周坤芳,任卓谊.GPS/INS深组合技术及其应用[J].舰船电子工程,2016,36(1):8-10.
ZHOU Kunfang, REN Zhuoyi. Application of Modular Technology of Tightly-coupled GPS/INS[J]. Ship Electronic Engineering, 2016, 36(1):8-10.
[9] 马宏阳,程鹏飞,黄华东.GPS/INS位置、速度和姿态全组合导航系统研究[J].测绘通报,2016(3):10-14.
MA Hongyang, CHENG Pengfei, HUANG Huadong. Research on the Complete Integrated GPS/INS Navigation System of Position,Velocity and Attitude[J]. Bulletin of Surveying and Mapping, 2016(3):10-14.
[10] 闫占杰,吴德伟,刘海波,等.GPS转发欺骗式干扰时延分析[J].空军工程大学学报:自然科学版,2013,14(4):67-70.
YAN Zhanjie, WU Dewei, LIU haibo, et al. Analysis of Time-delay in GPS Repeater Deception Jamming[J]. Journal of Air Force Engineering University: Natural Science Edition, 2013, 14(4):67-70.
[11] 阮冬茹,张莫.组合定位中选星算法的改进研究[J].测控技术,2015,34(8):111-113.
RUAN Dongru, ZHANG Mo. Research on Improving Stars Selecting Algorithm of Combination Positioning[J]. Measurement & Control Technology, 2015, 34(8):111-113.
[12] 张颂.GPS诱偏干扰暨局域导航一体化可行性研究[D].合肥:电子工程学院,2011.
ZHANG Song. A study of feasibility in GPS area-mapping deceiving unites battlefield navigation integrative system[D]. Hefei: Electronic Engineering College, 2011.
[13] 王艳奎.临近空间飞行器应用前景及发展分析[J].国防科技,2009,30(2):20-24.
WANG Yankui. An Analysis on Application Prospects and Development of Near-Space Vehicles[J]. National Defense Science & Technology, 2009, 30(2):20-24.
