基于堆叠降噪稀疏自动编码器的软件缺陷预测

薛参观

(1.南京航空航天大学计算机科学与技术学院,江苏 南京 210016；2.江苏省软件新技术与产业化协同创新中心,江苏 南京 210016)

0 引 言

软件缺陷预测[1]是提高和保证软件产品质量的关键技术之一。尽管很多学者已经对此问题进行了大量的探索，但其依然是一项艰巨而又有挑战性的工作[2]。刘芳等人[3]首先用主成分分析法对软件缺陷数据进行降维，消除冗余信息，然后用处理后的缺陷数据进行训练，构建软件缺陷预测模型；孟倩等人[4]使用粗糙集方法对软件缺陷数据进行属性约减，去掉冗余和无关的属性，再用支持向量机对软件缺陷进行分类预测；王海林等人[5]用基于关联规则的特征选择算法提取软件缺陷数据的特征，降低训练样本的维度，去除噪声属性，再用人工神经网络构建软件缺陷预测模型。这些方法都是先对软件缺陷数据进行特征提取，再结合机器学习等方法构建软件缺陷预测模型，而作为关键步骤的特征提取过程，它们都是采用浅层机器学习算法，很难获得软件缺陷数据的深层次本质特征。因此，如何自动从软件缺陷数据中提取与缺陷预测相关的深层特征成了一个重要的研究课题。

Hinton等人[6]提出的深度学习理论可以有效解决这个问题。深度学习的本质是将神经网络搭建成多层或多阶非线性信息处理的模型，使用有监督或无监督的特征映射获取原始数据的深层次本质信息。在进行分类预测时，将特征提取与分类器组合到一个框架中，用原始数据去自动学习特征，去除人工特征提取的过程，提高特征提取的效率[7]。目前将深度学习理论应用到软件缺陷预测中的主要研究有：Yang等人[8]用深度信念网络对软件缺陷进行特征提取，结合Logistic回归分类器构建软件缺陷预测模型；Wang等人[9]提出用深度信念网络自动学习软件程序源代码的语义语法特征，并利用学习到的特征训练和构建缺陷预测模型。

自动编码器[10]作为深度学习理论的重要组成部分，在无监督特征提取中扮演着重要角色，也被应用到多种领域。甘露等人[11]将改进的自动编码器应用于软件缺陷预测中，取得了不错的效果，但其实验数据量较小，容易造成训练欠拟合。Meng等人[12]对降噪稀疏自动编码器进行了研究，并分析了稀疏性约束和隐藏层节点数对数据重构和特征提取的影响，但其应用领域仅为手写字体的分类，Kumar等人[13]用于静态手势的特征提取，Sankara等人[14]用于指纹的特征提取，都证明了降噪稀疏自动编码器的有效性。

为了解决软件缺陷预测中特征提取面临的问题，获取软件缺陷数据深层次本质特征信息，提高预测精度，本文提出基于堆叠降噪稀疏自动编码器进行特征提取的软件缺陷预测方法，通过设置不同的隐藏层数和稀疏性约束，获取软件缺陷数据各层次的特征表示，然后用Logistic回归分类器进行分类预测，构建软件缺陷预测模型。

2 基于堆叠降噪稀疏自动编码器的软件缺陷预测方法

2.1 自动编码器

自动编码器(Auto-Encoder,AE)[11]是一种无监督学习算法，通过学习一个尽可能恢复自身的非线性编码，可以获取输入数据的深层次本质特征表示。自动编码器模型结构如图1所示，AE首先对输入数据进行编码，得到隐藏层的特征表示，然后对隐藏层的特征表示进行解码得到重构数据，再使用反向传播算法来训练网络，使得重构数据尽可能地等于输入数据，得到编码结果。

图1 自动编码器结构示意图

y(i)=fθ(x(i))=f(wx(i)+b)

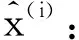
其中，θ′=(w′,b′),w′为权值矩阵，通常取w′=wT，b′为偏置向量。则对AE的网络参数优化调节实际上就是最小化重构误差：

其中，L(·)为代价函数。为了比较重构数据与输入数据之间的差异，通常有如下2种代价函数：

1)平方差代价函数：

2)交叉熵代价函数：

Nielsen[15]证明了交叉熵代价函数优于平方差代价函数，因此本文中选择交叉熵代价函数。自动编码器在整个训练样本集的代价函数为：

其中，第一项为整体代价项，第二项为规则化项，其目的是减小权重的幅度，防止过拟合。权重衰减系数λ用于控制两项的相对重要性。

2.2 稀疏自动编码器

稀疏自动编码器[16](Sparse Auto-Encoder,SAE)是在AE的基础上给隐藏神经元添加稀疏性约束而得到的。稀疏性约束是指激活最少(最稀疏)的隐藏神经元来表示输入数据的特征。

稀疏自动编码器在整个训练样本集的代价函数为：

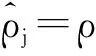
2.3 降噪稀疏自动编码器

降噪稀疏自动编码器[13](Denoising Sparse Auto-Encoder,DSAE)是在SAE的基础上，首先对输入数据进行加噪处理，再对加噪处理后的数据进行稀疏性编码，使得SAE必须学习去除这种噪声，迫使其学习输入数据更加鲁棒的表示，提高泛化能力。

图2 降噪稀疏自动编码器结构示意图

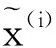
降噪稀疏自动编码器在整个训练样本集的代价函数为：

2.4 堆叠降噪稀疏自动编码器

将多个降噪稀疏自动编码器逐层叠加构建成深度神经网络模型，则称为堆叠降噪稀疏自动编码器(Stacked Denoising Sparse Auto-Encoder,SDSAE)，其可以获取输入数据更深层次的特征信息，越深的层次获取的特征信息具有越强的特征表示能力。

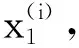
由于SDSAE的不同层是各自学习的，所以需要将它们组合成一个完整的深度网络，并对网络参数进行微调。微调过程是在预训练过程完成之后，SDSAE与分类器组合在一起，使用反向传播算法计算代价函数的偏导数，通过梯度下降法对网络参数进行迭代更新，同时调整所有层以获取最优化的网络参数的过程。

2.5 基于堆叠降噪稀疏自动编码器的软件缺陷预测方法

本文设计一个具有4个隐藏层的SDSAE用于软件缺陷数据的特征提取，并使用Logistic回归分类器对提取的特征进行分类的软件缺陷预测模型。在构建的预测模型中，为了学习到最优的网络参数，在预训练过程中，使用大量的无标签数据进行逐层贪婪训练，获得近似最优化的网络参数，在微调过程中，将包括分类器在内的整个深度网络进行微调，获得最优的网络参数。使用堆叠降噪稀疏自动编码器进行软件缺陷预测的具体步骤如下：

1)将软件缺陷数据集划分为训练数据集和测试数据集，并对训练数据集进行预处理；

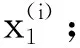
5)将步骤2～步骤4得出的特征表示和原始数据的标签分别作为Logistic回归分类器的输入构建软件缺陷预测模型；

6)通过梯度下降法分别对各阶特征表示构建的预测模型进行“微调”，优化深度网络中的参数；

7)将测试数据按训练数据相同的方法进行预处理后分别输入至训练好的预测模型，得出预测结果；

8)对得到的预测结果进行评价，得出结论。

使用堆叠降噪稀疏自动编码器进行软件缺陷预测的完整过程如图3所示。

3 实验与分析

3.1 实验准备

3.1.1 实验环境

本实验所用计算机配置为Intel(R) Xeon(R) E3-1230 3.30 GHz处理器，8 GB内存。实验所运行的软件环境为在Windows 7操作系统下安装的Matlab R2014a。

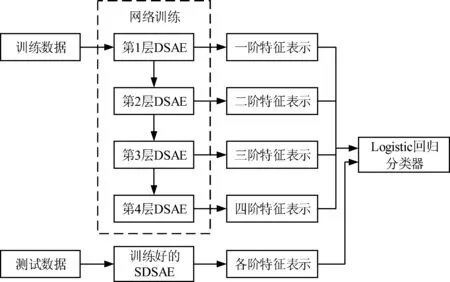
图3 基于SDSAE的软件缺陷预测过程

3.1.2 实验数据集

本文采用的实验数据为Eclipse缺陷数据集[17]，该数据集是软件缺陷预测领域应用较为广泛的公共数据集之一，可以从Eclipse Bug Data获取。Eclipse缺陷数据集有6个文件，分别对应于Eclipse的3个版本2种粒度下的故障记录，本文所采用的实验数据均为Eclipse 2.0版本files粒度的故障数据记录。

本文实验以软件发布后模块缺陷倾向性为预测目标，首先去除该数据集中所有非数值类型的特征，然后将发布后缺陷数量(post)转换为软件模块是否有缺陷的类标has_defects，转换方法为：若post=0，则has_defects=0，否则has_defects=1。经过处理后，数据集共有198个特征，主要包括软件规模度量特征、复杂性度量特征和基于语义语法树的度量特征等。该数据集中共有6729个样本，其中有缺陷样本为975个，缺陷率为14.49%。

3.1.3 超参数设置

本文实验中，由于数据集共198个特征，故输入层节点数设为198；权重衰减系数λ设为1e-3，稀疏性惩罚系数β设为3。本实验中，采用minFunc函数最小化DSAE的整体代价函数，minFunc是一个开源的Matlab函数，用于使用线性搜索方法对可微分真值多元函数进行无约束优化，可以从minFunc获取。在实验中，将代价函数优化方法指定为L-BFGS，并将最大迭代次数设为400。Logistic回归分类器的权重衰减系数设为1e-4，同样采用minFunc最小化其代价函数，最大迭代次数设为100。

3.2 评价指标

本文采用的评价指标为F1-度量，是综合衡量准确率和召回率的分类评价指标，其大小用来评价软件缺陷预测模型的好坏。F1-度量的计算公式为：

其中，准确率precision=TP/(TP+FP)，召回率recall=TP/(TP+FN)，TP是预测为有缺陷模块中确实有缺陷的软件模块数量，FP是预测为有缺陷模块而实际却无缺陷的软件模块数量，FN是预测为无缺陷模块而实际却有缺陷的软件模块数量。

3.3 实验结果及分析

为了验证降噪稀疏自动编码器DSAE对软件缺陷数据进行特征提取的能力，分别经过主成分分析法PCA[18]、线性判别分析法LDA[19]、独立成分分析法ICA[20]与降噪稀疏自动编码器DSAE进行特征提取构建缺陷预测模型，验证模型性能。其中：PCA累计贡献率设为0.95，DSAE的隐藏层单元数设为100，稀疏性约束设为0.2，加噪方式为掩蔽噪声，掩蔽率设为0.2。实验结果如图4所示，其中LR为文献[17]中所述没有经过特征提取，直接使用Logistic回归分类器构建缺陷预测模型的预测性能。由图4可以看出，使用DSAE对软件缺陷数据进行特征提取，不需要预先定义特征，只需将缺陷数据输入预测模型，其会自动学习，获取缺陷数据深层次本质特征。经过DSAE进行特征提取构建的缺陷预测模型，相比没有经过特征提取或经过PCA、LDA、ICA等方法进行特征提取的预测模型，在F1-度量上均有明显的提高，这表明DSAE对特征提取的效果比传统特征提取方法要好。

为了验证DSAE中微调和稀疏性约束对预测模型性能的影响，在实验中，设置只含一个隐藏层的DSAE构建缺陷预测模型，DSAE的隐藏层节点数设为100，稀疏性约束分别设为0.01、0.04、0.07、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0，实验结果如图5所示。从图5可以看出，未经过微调的预测模型在稀疏性约束小于0.4时呈增长趋势，在0.4～0.7区间内呈下降趋势，大于0.7时变得不稳定，而经过微调的预测模型在不同稀疏性约束情况下均能表现出良好的预测性能，且均比未经过微调的预测模型的性能优越。分析原因，未经过微调的预测模型当稀疏性约束小于0.4时，DSAE的隐藏神经元激活数随着稀疏性约束的增大而增多，使DSAE可以学习原始数据更本质的特征表示，因此预测性能增加；当稀疏性约束在0.4～0.7之间时，DSAE的隐藏神经元需要激活的过多，这将造成训练过拟合，因此预测性能会降低；但当稀疏性约束大于0.7时，意味着隐藏层中的大多数神经元都需要激活，这种不合理的设置会破坏网络参数正常的优化，虽然预测模型仍然具有预测能力，但其网络参数已经不是通过“学习”得到的，所以得到的预测模型属于无效预测模型。而经过微调的预测模型的网络参数已经在分类器的监督下进行了调整，使得DSAE的稀疏性约束设置对预测模型的影响消失，因此，经过微调的预测模型在不同稀疏性约束下均能表现出良好的性能。

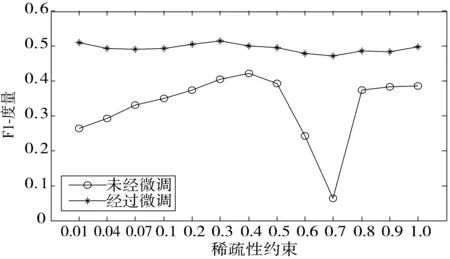
图5 微调和稀疏性约束对预测性能的影响

为了验证SDSAE中模型深度和稀疏性约束对预测性能的影响，在实验中，设置含有4个隐藏层的预测模型，隐藏层单元数为150-100-50-30，稀疏性约束分别为0.05、0.1、0.2、0.3、0.4、0.5，实验结果如图6所示。从图6可以看出，对于相同的模型深度，当稀疏性约束小于0.3时，其值越大，预测性能越好，但大于0.3时，又略有降低。与此同时，对于相同的稀疏性约束，网络深度越深，预测性能越好。分析原因，是由于深度模型可以获取输入数据更深层次的特征信息，越深的层级获取的特征信息具有越强的特征表达能力，因此预测模型深度越深预测性能越好。但并不是模型深度越深越好，其深度取决于预测模型与训练数据的规模，当预测模型深度太深时，会造成“梯度消失”现象，从而不能完成模型训练，得不到预测结果；并且从图6还可以看出，预测模型的深度越深，预测性能相对提升得越少，甚至可能造成训练过拟合，降低预测性能，所以不能盲目地增加模型深度。

图6 隐藏层数和稀疏性约束对预测性能的影响

为了验证SDSAE中掩蔽噪声的不同掩蔽率对预测性能的影响，在实验中，设置SDSAE的隐藏层为4层，隐藏层单元数为150-100-50-30，稀疏性约束设为0.3，掩蔽噪声的掩蔽率分别为0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0，实验结果如图7所示。从图7可以看出，对于加入掩蔽噪声相同掩蔽率的预测模型，模型深度越深预测性能越好。而对于相同的模型深度，掩蔽噪声的掩蔽率越大，预测性能越差。分析原因，是由于预测模型在训练时，掩蔽噪声会掩蔽掉训练数据中与软件缺陷有相关性的数据，即对缺陷预测有益的信息，因此掩蔽率越大，预测模型的性能越差。当掩蔽率为1.0时，所有训练数据都被掩蔽，虽然预测模型具有预测能力，但其网络参数并不是根据训练数据“学习”得到的，因此得到的预测模型属于无效模型，其预测结果也不是有效的预测结果。但对预测模型的训练数据中加入噪声，可以使学习到的预测模型鲁棒性更高，泛化能力更强，因此掩蔽噪声的掩蔽率应设置在一个合理的范围。

图7 掩蔽噪声的掩蔽率对预测性能的影响

4 结束语

为了解决软件缺陷预测中传统的特征提取方法不能提取出软件数据中深层次本质特征的问题，本文提出一种基于堆叠降噪稀疏自动编码器的软件缺陷预测方法，其首先用堆叠降噪稀疏自动编码器对软件缺陷数据进行特征提取，然后用Logistic回归方法对提取后的特征表示进行分类预测，取得了较好的预测效果。但由于预测模型的性能受模型深度、稀疏性约束、掩蔽率等超参数的影响，而超参数的选择并没有统一的理论指导，因此对超参数的选择是今后研究的主要课题。

参考文献：

[1] 王青,伍书剑,李明树. 软件缺陷预测技术[J]. 软件学报, 2008,19(7):1565-1580.

[2] 陈翔,顾庆,刘望舒,等. 静态软件缺陷预测方法研究[J]. 软件学报, 2016,27(1):1-25.

[3] 刘芳,高兴,周冰,等. 基于PCA-ISVM的软件缺陷预测模型[J]. 计算机仿真, 2014,31(3):397-401.

[4] 孟倩,马小平. 基于粗糙集-支持向量机的软件缺陷预测[J]. 计算机工程与科学, 2015,37(1):93-98.

[5] 王海林,于倩,李彤,等. 基于CS-ANN的软件缺陷预测模型研究[J]. 计算机应用研究, 2017,34(2):467-472.

[6] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006,313(5786):504.

[7] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015,521(7553):436-444.

[8] Yang Xinli, Lo D, Xia Xin, et al. Deep learning for just-in-time defect prediction[C]// IEEE International Conference on Software Quality, Reliability and Security. 2015:17-26.

[9] Wang Song, Liu Taiyue, Tan Lin. Automatically learning semantic features for defect prediction[C]// ACM International Conference on Software Engineering. 2016:297-308.

[10] Deng Li, Seltzer M, Yu Dong, et al. Binary coding of speech spectrograms using a deep auto-encoder[C]// Conference of the International Speech Communication Association. 2010:1692-1695.

[11] 甘露,臧洌,李航. 基于DA-SVM的软件缺陷预测模型[J]. 计算机与现代化, 2017(2):36-39.

[12] Meng Lingheng, Ding Shifei, Xue Yu. Research on denoising sparse autoencoder[J]. International Journal of Machine Learning & Cybernetics, 2016,31(5):1-11.

[13] Kumar V, Nandi G C, Kala R. Static hand gesture recognition using stacked denoising sparse autoencoders[C]// IEEE International Conference on Contemporary Computing. 2014:99-104.

[14] Sankaran A, Pandey P, Vatsa M, et al. On latent fingerprint minutiae extraction using stacked denoising sparse AutoEncoders[C]// IEEE International Joint Conference on Biometrics. 2014:1-7.

[15] Neilsen M. Neural Networks and Deep Learning[M]. Determination Press, 2015.

[16] Jiang Xiaojuan, Zhang Yinghua, Zhang Wensheng, et al. A novel sparse auto-encoder for deep unsupervised learning[C]// The 6th IEEE International Conference on Advanced Computational Intelligence. 2013:256-261.

[17] Zimmermann T, Premraj R, Zeller A. Predicting defects for Eclipse[C]// IEEE International Workshop on Predictor Models in Software Engineering.2007:9.

[18] Vidal R, Ma Yi, Sastry S S. Principal Component Analysis[M]. IEEE Computer Society, 2005.

[19] Ye Junxiao, Janardan R, Li Q. Two-dimensional linear discriminant analysis[C]// Proceedings of the 8th Annual Conference on Neural Information Processing Systems. 2004:1569-1576.

[20] Choi S. Independent Component Analysis[M]. Springer Berlin Heidelberg, 2012.