基于深度强化学习DDPG算法的投资组合管理
2018-06-04黄硕华
齐 岳,黄硕华
(1.南开大学商学院,天津 300071; 2.南开大学中国公司治理研究院,天津 300071;3.中国特色社会主义经济建设协同创新中心,天津 300071)
0 引 言
投资组合管理是将一定资金分配给多个金融资产的决策过程,通过不断改变分配权重来提高收益,减小风险[1]。已经有学者从理论方面对投资组合优化进行了详尽的研究[2-3],但是由于金融资产价格难以预测,交易数据体量庞大,并具有严重非线性,在实践中仅靠人脑难以做出最优决策。然而随着人工智能技术的发展,利用计算机进行自我学习和大量计算,并实现优化的投资组合管理已经成为可能。自从击败人类顶尖围棋高手的AlphaGo问世以来,深度强化学习[4]成为人工智能领域的研究热点,这种技术被应用于包括金融等多个领域,展现出强大的实力,因此深度强化学习在金融领域有很广阔的应用前景。
深度学习[5]和强化学习[6]都是人工智能的重要分支,深度学习是指采用深度神经网络进行学习的方法,对于求解复杂的非线性问题具有较大优势;强化学习则是与监督学习和无监督学习对等的学习模式,善于求解复杂的优化决策问题。这2种方法都可以单独应用于金融领域。
目前深度学习和强化学习在金融领域的研究主要集中在预测单个资产价格趋势,例如Selvin等人[7]使用LSTM(Long Short Term Memory Network), RNN(Recurrent Neural Network)和CNN(Convolutional Neural Network)这3种不同的深度学习网络对一组上市公司的价格进行预测并比较它们的表现,采用滑动窗口方法,预测短期内的价值;Khare等人[8]对比了多层前馈神经网络和LSTM应用于股票价格预测的效果,发现多层前馈神经网络预测精度优于LSTM;曾志平等人[9]提出了基于深度信念网络对短期内金融资产价格的涨跌进行预测,准确率较高;李文鹏等人[10]构建3层深度神经网络模型对股票价格趋势进行预测,获得了较高的正确率。为了对2个资产进行配对交易,胡文伟等人[11]提出了结合Sarsa强化学习方法和自适应模式动态参数优化方法的配对交易策略,提升了交易系统的获利能力并降低回撤风险。Li等人[12]使用中国股市2008-2015年的历史数据,通过SVM和LSTM预测股价趋势,实验结果表明LSTM要优于SVM。孙瑞奇[13]采用BP(Back Propagation)神经网络、RNN和LSTM,预测标普500指数在2013年3月-2015年9月的收盘价,与BP神经网络相比,RNN由于考虑了时间序列的时序关系的影响,预测精度比BP神经网络高,而LSTM是在RNN基础上改进的,因此预测精度更高。然而在投资组合交易决策方面,深度学习和强化学习方法的研究尚有空白。
深度强化学习是一种将深度学习与强化学习结合的方法,由Google的DeepMind团队于2015年首次提出并应用于游戏[14-15],近年来,已经有学者将深度强化学习应用于金融领域。例如,Deng等人[16]将其应用于单个金融资产的交易,使用深度学习网络对市场状态进行学习,使用强化学习做出交易决策,并在股票和期货市场得到了验证。Jiang等人[17]采用深度确定性策略梯度DDPG算法进行虚拟货币交易,并获得极高收益。Zhang等人[18]采用DDPG方法,通过判断最佳股票并投入绝大多数资金的方式,获得较高收益。这些研究仍是集中于单个金融资产的交易,或者虽然针对多个金融资产[17-18],但是将投资权重几乎全部集中在一个金融资产上,更类似于每次从几种金融资产中择优下注,而非投资组合管理。
综上所述,目前还没有学者将深度强化学习技术应用于中国股票市场的投资组合管理。本文首次将深度强化学习的DDPG算法进行改进,使之能够应用于投资组合管理问题。通过限制投资组合中单个风险资产所占的总资金量的权重,达到分散风险的目的,并采用丢弃算法(Dropout)[19],即在训练模型时随机丢弃一些节点的方法,解决过拟合的问题,提高投资效益。本文实验以中国股票市场为例,选取16只中证100指数成分股作为风险资产,实验结果表明本文基于深度强化学习构建的投资组合,2年累计价值增幅达到65%,显著高于其对照组,表明本文的方法是非常有效的。而且通过进一步实验,表明当用于训练的数据距离实际测试的时间越近,则本文构建的投资组合表现越好。
1 深度学习与强化学习概述
1.1 深度学习
深度学习是一种利用多层非线性变换处理网络结构来进行表征学习的通用框架。得益于计算机性能的提升,深度学习大大提升了人工神经网络方法的有效性,是近年来人工智能领域的重要方法。
传统人工神经网络随着神经网络层数的增加,容易出现局部最优解或过拟合问题,因此不适用于深层网络;另外需要人工设计数据特征并进行数据标记,使得学习耗时耗力。
深度学习的概念由加拿大多伦多大学的Hinton等人[20]于2006年提出,基于深度信念网络DBN(Deep Belief Network)提出无监督逐层预训练和有监督调优算法,可以自动学习数据特征并对学习结果进行有效的优化,解决了深层神经网络结构容易出现局部最优解的问题以及需要人工设计数据特征的问题。后来,Hinton又提出了Dropout方法解决神经网络过拟合问题[19]。之后深度学习快速发展,并且在语音、图像、医疗、金融等领域应用广泛。
深度学习常见的网络结构包括深度神经网络DNN(Deep Neural Networks)、深度信念网络DBN、卷积神经网络CNN、循环神经网络RNN、LSTM等。
1.2 强化学习
强化学习,又称为增强学习或再励学习。强化学习的主体是智能体,其主要思想是智能体与环境交互和试错,利用评价性的反馈信号实现决策的优化。当智能体的某个动作导致环境正的奖赏或回报,即为强化信号,则智能体以后产生这个动作的趋势便会加强;反之,智能体产生这个动作的趋势会减弱[21]。强化学习主要有4个要素,即策略、回报、动作和环境。强化学习的目标是学习一个策略,使得智能体选择的动作能够获得环境最大的回报。回报可以用一个函数来计算,又称为回报函数。为了衡量强化学习的长期效果,通常用值函数(value function)来代替回报函数,不仅衡量动作的即时回报,还衡量从该状态起随后一系列可能的状态所累积的回报。
经典的强化学习方法往往无法解决状态和动作空间维度很高的问题,一个有效的解决方法是使用函数近似,即将值函数或者策略用一个函数来表示。常用的近似函数有线性函数、核函数、神经网络等。近年来最成功的函数近似方法就是使用深度神经网络作为强化学习的非线性近似函数[22],将深度学习和强化学习相结合,即为深度强化学习。深度强化学习由DeepMind团队于2015年首次提出之后,将其发展并分别应用于打败人类围棋冠军的AlphaGo[23]和更强的AlphaGo Zero[24]。然而这时的深度学习技术DQN(Deep Q-Learning)依然解决的是离散动作的问题,无法直接应用于权重连续的投资组合管理。DeepMind团队于2016年提出的深度确定性策略梯度方法即DDPG算法[25],解决了连续动作空间的强化学习问题。DDPG算法是一种无模型的离策略Actor-Critic强化学习方法,利用深度神经网络来学习连续动作空间的策略,DDPG算法中,策略是参数化的,通过策略梯度方法,直接优化深度神经网络的参数。
2 问题描述与模型表示
投资组合管理是指通过不断改变资金在金融资产上的分配权重,从而最大限度提高回报率并降低风险的过程。在投资组合管理中,各项资产的权重是连续的变量,需要通过深度强化学习网络进行自我学习和大量计算,在实现总收益最大化的目标下,在每个交易时刻之前输出一次最优权重,并通过自动交易将投资组合各项资产的比例调整到最优权重,从而实现优化的投资组合管理。
2.1 模型假设
在现实中,金融市场运行情况较为复杂,例如较大的资金量可能会对市场价格产生影响,交易成本不一定与交易额成正比,投资者可能无法恰好以收盘价买入或卖出股票,以及投资者可能不能购买非整股股票。但为了适当简化复杂的投资组合管理问题,本文作出以下假设:
假设1交易资金量足够小,以至于不会对市场中其他投资者行为以及金融资产价格造成影响。
假设2交易成本为当日交易额的固定比例。
假设3交易过程中能够将收盘价作为股票交易的成交价格。
假设4投资者能按照最优的资金分配权重购买任意数量的股票,包括购买股票数可以为非整数。
2.2 投资组合的资产组成
本文的投资组合由N+1种金融资产组成,分别包括N项风险资产和一种货币(人民币)。之所以将货币作为投资组合中的一种资产,是为了方便深度强化学习的网络进行计算,投资组合的总权重被设为1,这时如果组合中仅包括风险资产,就会使得在市场表现不佳时,投资者也需全仓持有风险资产,使得收益率降低,且增加风险。而将货币作为投资组合中的一种资产,则当市场表现不佳时,可以仅持有货币,即相当于不持有风险资产。
2.3 投资组合的资产权重与收益
设yt为用向量表示的投资组合各项资产在区间[t-1, t]上的投资收益率,将之称为收益向量,具体表示如下:
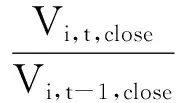
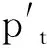
(1)
设Rt为投资组合在t时刻的累计总收益率,即:
(2)
用wt表示投资组合各项资产在[t-1,t]时刻所占的权重,将之称为权重向量,具体表示如下:
wt=[w1t,w2t,w3t,…,w(N+1)t]
因此易知
(3)
2.4 考虑交易费用的投资组合收益
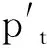
(4)
将式(3)、式(4)相乘,并分别代入式(1)、式(2)中,可知:
rt=(1-μt)wtyt
(5)
(6)
2.5 缺失数据处理
在股票市场中,可能存在个别股票停牌的现象,此时单只股票的价格数据为空白,因此将停牌期间的价格设为停牌之前最后一个交易日的收盘价,避免影响整体的运算。
此外周末和节假日为非交易日,此时所有股票的数据都为空白,因此直接将非交易日的数据全部去掉,不会影响到整体数据的计算。
3 实验数据输入
在本文的实验中,从中证100指数成分股中选取16只股票作为风险资产,因此N=16,再加上货币,构成投资组合中的N+1=17种金融资产。其中,选取的中证指数成分股股票代码如下:600011,600015,600016,600028,600030,600036,600048,600115,600276,600518,600519,600585,600837,600999,601006,601009。
将交易成本占交易额的比例设为0.025%,这个数值的设定对于中国的股票市场是很合理的,而且由于中国股票市场规定当日买入的股票只能次日或之后才能卖出,因此选用每个交易日最多交易一次的交易频率,同时为了简化模型的难度,设定交易时间间隔必须为整数天。
4 DDPG算法结构
强化学习的基本要素包括智能体Agent、环境、状态s、策略π、动作a、回报r。Agent从环境感知当前状态st,根据策略π选择动作at,作用于环境,得到回报rt,转换到下一状态st+1。由于回报rt只能反映当前动作和状态的回报,不能反映对未来回报的影响,因此又引入了值函数v,v包含当前回报和未来估计的折扣(用γ表示)回报。深度强化学习方法利用深度神经网络来学习连续动作空间的策略,将策略进行参数化表示,输出即为动作。
DDPG算法采用强化学习的Actor-Critic[16]架构,由4个神经网络组成:2个结构相同的Actor策略网络,分别为Actor_online网络和Actor_target网络;2个结构相同的Critic评价网络,分别为Critic_online网络和Critic_target网络。其中Actor_target和Critic_target网络主要用于产生训练数据集,而Actor_online和Critic_online网络主要用于训练优化网络参数。根据引言部分的分析,与其他神经网络相比LSTM网络更适合于时间序列数据的预测[12-13],因此本文的算法中采用LSTM。
2个Actor策略网络都是由一个长短时记忆网络层LSTM、一个全连接网络层(FC)和一个softmax层组成的,其中全连接网络层的激活函数采用线性纠正函数(ReLU)。网络输入为状态,即资产价格st,输出为买卖动作at。
2个Critic评价网络都是由一个LSTM网络层、一个FC全连接网络层(输入为资产价格st)和一个FC全连接网络层(输入为动作at)组成,最后2个FC相加后接入另一个FC全连接网络层。网络输入为资产价格st和买卖动作at,而输出为估计的未来折扣回报γqt+1。
DDPG算法结构如图1所示。
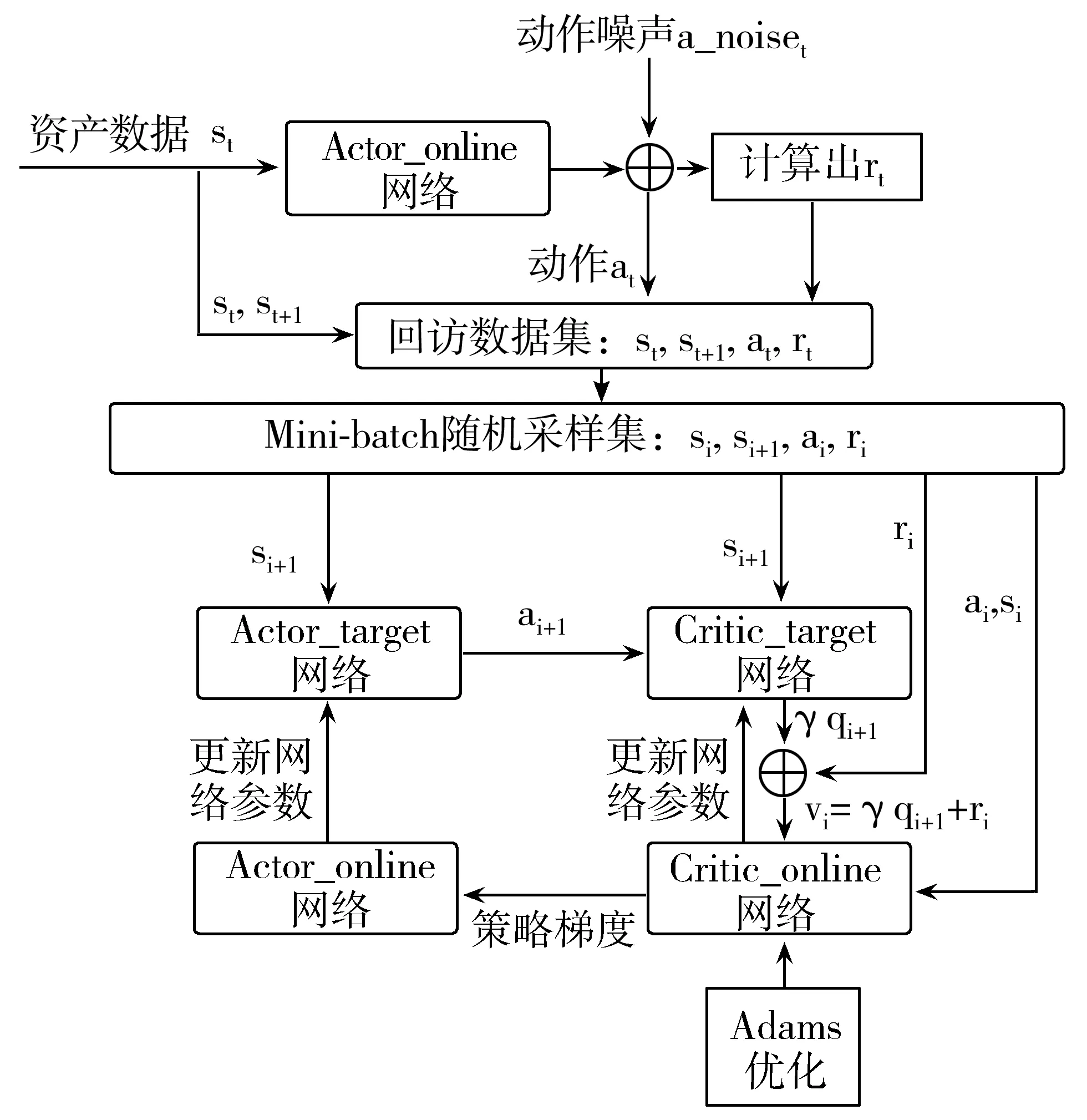
图1 DDPG算法架构
DDPG算法具体步骤如下:
1)Actor_online网络产生回放数据集:根据资产价格st输出初始动作,再加上随机噪声a_noiset输出动作at,并计算即时回报rt,即公式(5)所示的当前收益率;转换到下一状态,即下一时刻资产价格st+1。于是得到训练数据集,也称为回放数据集,由(st,at,rt,st+1)构成。
2)对回放数据集进行Mini-batch采样,即每次随机采样相同数目且连续的样本作为网络的训练数据。用(si,ai,ri,si+1)表示单个Mini-batch中的一组数据。
3)使用Mini-batch采样数据估计值函数vi。由Actor_target网络计算动作ai+1,由Critic_target网络计算未来折扣回报γqi+1,最后计算值函数vi=ri+γqi+1。
4)使用Mini-batch采样数据和计算的值函数vi对Critic_online网络进行训练,采用Adams(Adaptive Moment Estimation)方法进行优化,同时由Critic_online网络通过策略梯度对Actor_online网络进行优化。
5)最后由Critic_online网络和Actor_online网络分别更新Actor_target网络和Critic_target网络的参数。
5 DDPG算法实现及问题解决
5.1 软件环境
计算机操作系统为Windows10,运行环境为Tensorflow1.4,采用Python3.6编程语言。
5.2 遇到的问题及解决办法
在实际训练网络时主要发现了过拟合和资产权重分配不合理的问题,下面具体分析产生的原因和解决办法。
1)过拟合。
在算法实现的过程中,神经网络容易出现在训练中效果良好而在测试中表现不佳的现象,说明这时网络过于依赖训练数据集,因此当新数据出现时无法有效处理,也就是出现了过拟合现象。为了解决该问题,采取以下措施:在所有的LSTM网络中增加Dropout选项;适当减少数据集的采样次数(Max Step);改变输入资产数据的窗口长度(Window Length),“窗口长度”为在交易过程中设置的历史数据天数,用于计算当前的最优权重。
2)资产权重过于集中。
由于强化学习是以马尔科夫决策过程为基础的[6],即认为未来的回报与过去的状态无关,仅与当前和未来状态有关。由于投资组合的风险(即方差)需要根据历史数据计算得到,若将投资组合的风险最小化作为优化目标,就会使得未来的回报与过去的状态有关。因此本文采用的方法将值函数v(即当前收益率加上未来折扣收益率)最大化作为唯一的优化目标,因而无法同时做到风险最小化。但是,为了通过投资组合适当分散非系统风险,可以对原始权重进行进一步处理,做到在尽量不影响投资组合表现的前提下,适当对组合中的各项资产权重进行分散,从而达到优化收益、减小风险的目的。具体过程如图2所示。
首先判断出原始权重中的最大值并设为wmax1,判断wmax1是否大于0.7,若不大于0.7,则说明输出的原始权重已经达到一定程度的风险分散,此时直接将原始权重作为最终权重。若wmax1大于0.7,则说明投资组合的权重过于集中于一个金融资产,这时需要对权重进行处理。
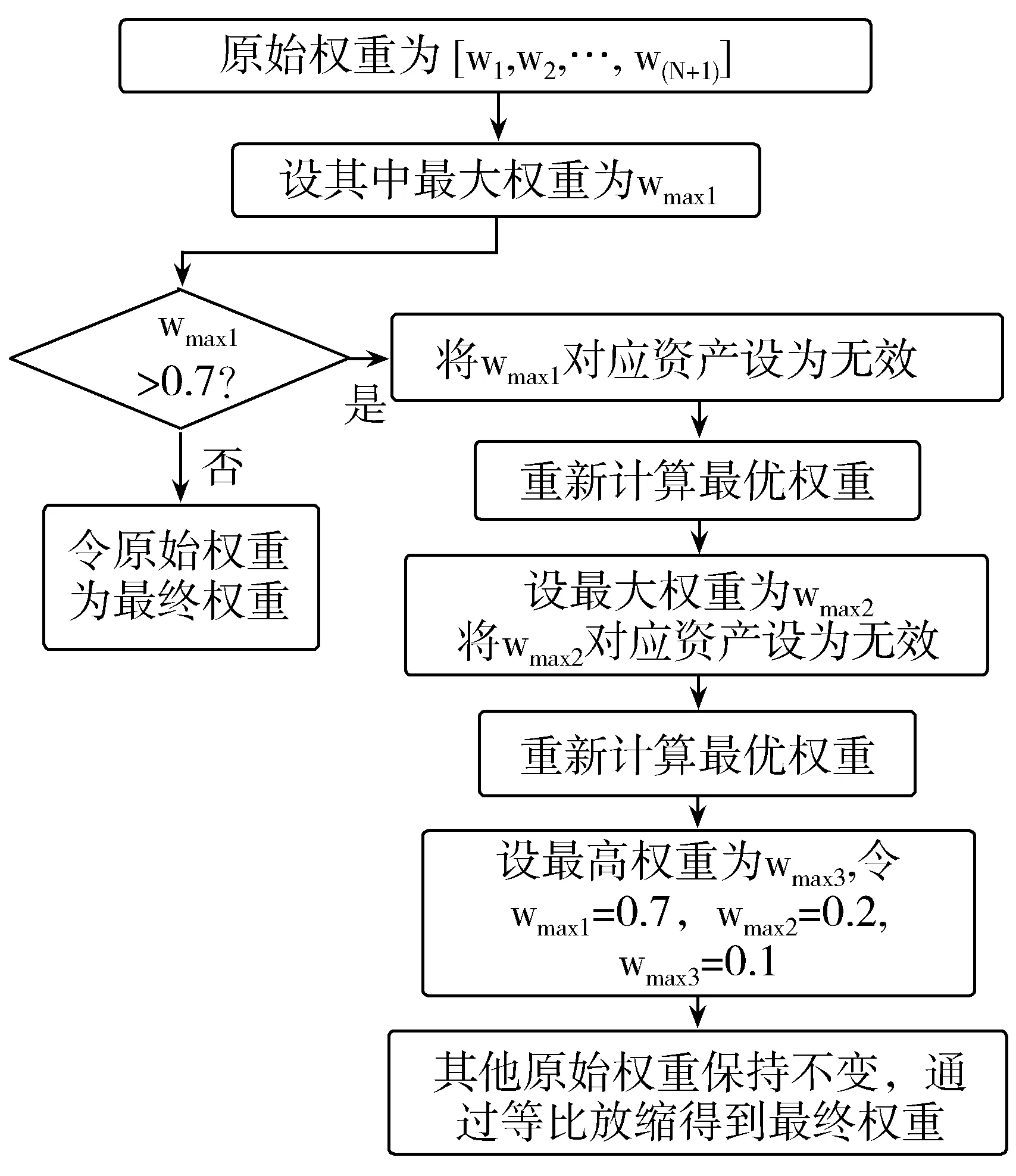
图2 投资组合的权重限制实现
接着将wmax1对应的资产设为无效,重新利用神经网络计算一组新的最优权重,将第二次得到的权重中的最大值设为wmax2,并继续将其对应的资产设为无效。继续重新计算最优权重,将第三次的最大值设为wmax3。
令wmax1=0.7,wmax2=0.2,wmax3=0.1,其他权重保持不变,此时所有资产权重的总和可能超过1。之后通过等比缩放,使得所有资产的权重的总和变为1,得到最终权重。注意,由于中国的股票市场不允许做空,因此需要设定单个资产的权重不为负。
6 实验结果
本文选取16只中证100指数成分股从2011年7月18日-2018年1月15日的收盘价作为实验数据。其中共包括1581个交易日,将其中约2/3的数据,即1000个交易日,作为神经网络的训练数据,剩余的581个交易日作为测试数据。因此训练数据由2011年7月18日-2015年8月27日的收盘价组成,测试数据由2015年8月28日-2018年1月15日的收盘价组成。先对神经网络进行训练,并用训练好的神经网络对测试数据进行交易,就可得到实验结果。
由于本文中的实验是先随机挑选16只股票作为风险资产,再用这16只股票构建投资组合,并没有选择其他股票的权利,所以与现实中主动型股票基金情况不同,不能进行直接的绩效对比。因此为了评价本文方法的结果,构建另一个投资组合作为对照组(等权重组合),即假设该组合在最初分配给各项风险资产的权重都是1/16,并不改变权重一直持有至期末。
本文实验的窗口长度为6天;Dropout的概率为0.8,即在训练过程中LSTM网络中每个节点没有被丢弃的可能性为0.8。
实验结果如图3所示。
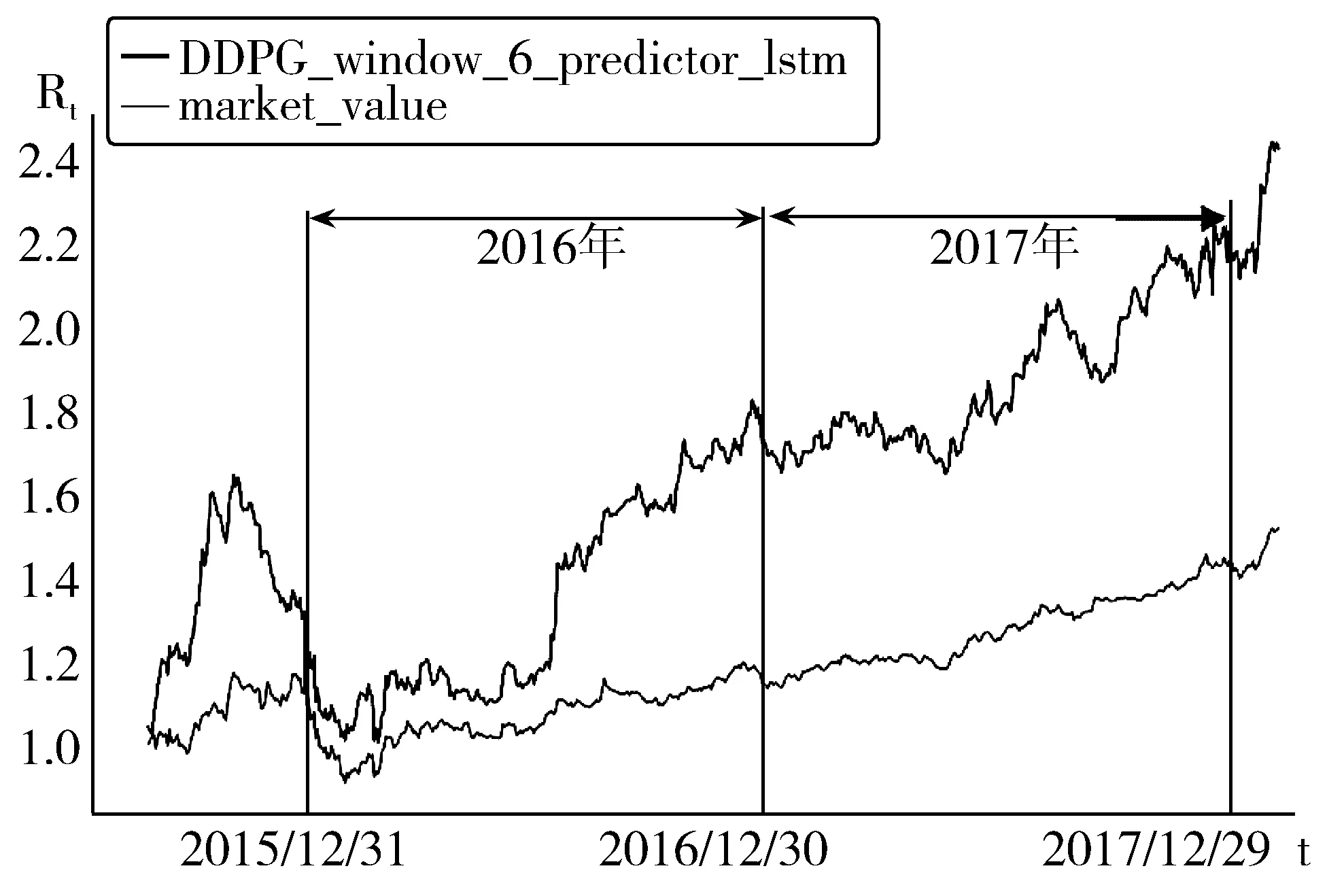
图3 本文投资组合与对照组的总价值变化
图3中的横坐标为时间t,纵坐标为公式(6)中的累计收益率Rt,其中DDPG_window_6_predictor_lstm对应的曲线为本文构建的投资组合的价值,而market_value则为对照组(等权重组合)的市场价值。从图3中可以清晰地看出本文采用深度强化学习构建的投资组合的收益要显著高于等权重组合。之后进一步对实验数据进行分析。
2015年8月28日为交易开始的时间,此时本文组合和对照组的价值为初始价值,将其设为p0,并用p0的倍数来表示之后不同时间节点的本文投资组合与对照组价值。选取每年最后一个交易日作为关键时间节点,将相应数据进行汇总和对比,结果如表1所示。
表1 本文投资组合与对照组的价值对比

项 目本文组合对照组2015年8月28日总价值p0p02015年12月31日(最后一个交易日)总价值1.33 p01.15 p02016年12月30日(最后一个交易日)总价值1.69 p01.17 p02017年12月29日(最后一个交易日)总价值2.20 p01.45 p0
根据表1中的数据分别计算出本文投资组合与对照组的2016年增幅、2017年增幅、2016-2017年期间的几何平均价值增幅以及2016-2017年期间总增幅,结果如表2所示。
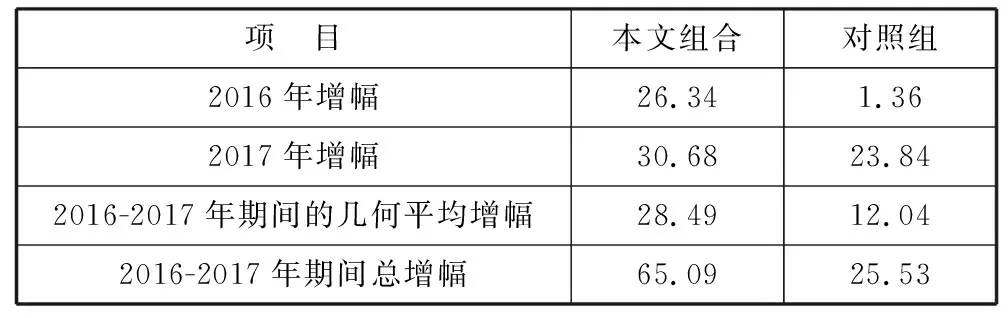
表2 本文投资组合与对照组的价值增幅对比 单位:%
从表2可以看出,本文采用深度强化学习构建的投资组合价值增幅在不同区间都显著高于对照组,说明本文方法进行的积极型投资组合管理取得较好的效果,本方法的应用价值得到了证实。
不过,本文投资组合的价值增幅在2016年比对照组高了24.98%,但在2017年却仅比对照组高了6.84%,因此可以认为本文构建的投资组合在2016年的表现优于2017年。这可能是因为训练集包含的是2011年7月18日-2015年8月27日的历史数据,经过这些数据训练出来的神经网络仅仅学会了这一时间段存在的市场规律。当被应用于2017年时,由于与训练数据时间的间隔过长,市场情况已经发生了变化,原有规律有一部分已经不能完全适用,因此导致本方法在距离训练数据时间较近的2016年表现要优于较远的2017年。
为了验证这一猜想,进一步进行实验,仍采用2011年7月18日-2018年1月15日的收盘价作为实验数据。将实验数据中的前1250个交易日作为训练数据,剩余的331个交易日作为测试数据。因此训练数据由2011年7月18日-2016年9月5日的收盘价组成,测试数据由2016年9月6日-2018年1月15日的收盘价组成。测试结果如图4所示。
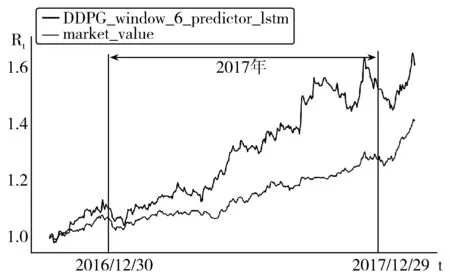
图4 进一步实验中本文组合与对照组总价值变化
从图4可知,当在训练数据集中加入2016年的数据之后,本文投资组合的表现显著优于之前对照组。对投资组合价值的增幅进行计算,得到表3的结果。对比表2中未加入2016年数据训练的实验结果,发现本文投资组合的表现明显变好,证实了训练数据与测试数据的时间间隔越短,则训练效果越好的猜想。

表3 本文投资组合与对照组的价值增幅对比 单位:%
综上所述,本文方法进行的积极型投资组合管理所构建的投资组合具有较好的效果,这一方法的应用价值得到了证实。
7 结束语
由于目前还没有深度强化学习技术在投资组合管理的应用,本文首次将深度强化学习的DDPG算法进行改进,使之能够应用于投资组合管理,通过限制投资权重,分散了风险,并采用丢弃算法,解决了过拟合问题。本文以中国股票市场为例,选取了16只中证100指数成分股,作为投资组合中的风险资产进行实验。实验结果表明,本文方法构建的投资组合表现远超其他对照组,表明了本文方法的有效性。但是本文方法为了适当简化而提出了一些假设,例如假设交易资金量足够小,以至于不会对市场中其他投资者行为以及金融资产价格造成影响,但当本方法的使用者为机构投资者或资金量较大的个人投资者时,就需要考虑自身交易对市场价格带来的影响,因此有必要进行更深入的研究。此外,虽然本文仅针对中国股票市场进行了实验,但这一方法对于期货市场和外汇市场是否也适用,有待于进一步探索。
参考文献:
[1] Markowitz H M. Portfolio Selection: Efficient Diversification of Investments[M]. 2nd Ed. New Jersey: Wiley, 1991.
[2] Qi Yue, Wang Zhi-hao, Zhang Su. On analyzing and detecting multiple optima of portfolio optimization [J]. Journal of Industrial and Management Optimization, 2018,14(1):309-323.
[3] Qi Yue. On the criterion vectors of lines of portfolio selection with multiple quadratic and multiple linear objectives[J]. Central European Journal of Operations Research, 2017,25(1):145-158.
[4] 赵冬斌,邵坤,朱圆恒,等. 深度强化学习综述: 兼论计算机围棋的发展[J]. 控制理论与应用, 2016,33(6):701-717.
[5] 李玉鑑,张婷. 深度学习导论及案例分析[M]. 北京:机械工业出版社, 2016.
[6] 王雪松,朱美强,程玉虎. 强化学习原理及其应用[M]. 北京:科学出版社, 2014.
[7] Selvin S, Vinayakumar R, Gopalakrishnan E A, et al. Stock price prediction using LSTM, RNN and CNN-sliding window model[C]// 2017 International Conference on Advances in Computing, Communications and Informatics. 2017:1643-1647.
[8] Khare K, Darekar O, Gupta P, et al. Short term stock price prediction using deep learning[C]//2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology. 2017:482-486.
[9] 曾志平,萧海东,张新鹏. 基于DBN的金融时序数据建模与决策[J]. 计算机技术与发展, 2017,27(4):1-5.
[10] 李文鹏,高宇菲,钱佳佳,等. 深度学习在量化投资中的应用[J]. 统计与管理, 2017(8):104-106.
[11] 胡文伟,胡建强,李湛,等. 基于强化学习算法的自适应配对交易模型[J]. 管理科学, 2017,30(2):148-160.
[12] Li Wei, Liao Jian. A comparative study on trend forecasting approach for stock price time series[C]//2017 11th IEEE International Conference on Anti-counterfeiting, Security, and Identification. 2017:74-78.
[13] 孙瑞奇. 基于LSTM神经网络的美股股指价格趋势预测模型的研究[D]. 北京:首都经济贸易大学, 2015.
[14] Mnih V, Kavukcuoglu K, Silver D, et al. Playing Atari with deep reinforcement learning[C]// Advances in Neural Information Processing Systems. 2013:1-9.
[15] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015,518(7540):529-533.
[16] Deng Yue, Bao Feng, Kong Youyong, et al. Deep direct reinforcement learning for financial signal representation and trading[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017,28(3):1-12.
[17] Jiang Zhengyao, Xu Dixing, Liang Jinjun. A Deep Reinforcement Learning Framework for the Financial Portfolio Management Problem [DB/OL]. https://arxiv.org/abs/1706.10059, 2017-11-30.
[18] Zhang Chi, Zhang Limian, Chen Corey. Deep Reinforcement Learning for Portfolio Management[DB/OL]. http://www-scf.usc.edu/~zhan527/post/cs599, 2017-11-18.
[19] Srivastava N, Hinton G, Krizhevsky A. Dropout: A simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014,15(1):1929-1958.
[20] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006,313(5786):504-507.
[21] 陈学松,杨宜民. 强化学习研究综述[J]. 计算机应用研究, 2010,27(8):2835-2844.
[22] 李晨溪,曹雷,张永亮,等. 基于知识的深度强化学习研究综述[J]. 系统工程与电子技术, 2017,39(11):2603-2613.
[23] Silver D, Huang Aja, Maddison C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016,529(7587):484-489.
[24] Silver D, Schrittwieser J, Simonyan K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017,550(7676):354-359.
[25] Timothy P L, Jonathan J H, Alexander P. Continuous control with deep reinforcement learning[C]// International Conference on Learning Representations. 2016:1-14.
