基于极限学习机的武器装备作战效能全局敏感性分析
2018-06-04张德平
董 雪,张德平
(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)
0 引 言
作战效能是指武器装备系统在作战中发挥作用的有效程度[1],是衡量武器价值的重要指标。在有限的预算和时间内提升武器的作战效能,是武器装备发展的重点。作战效能是多指标综合作用的结果,由于预算和时间的限制,提高武器作战效能最有效的途径是找到对武器作战效能影响较大的影响因素,即对武器作战效能指标进行敏感性分析与筛选,进而找到与其相关联的作战设备,进行功能的完善与提高,从而提高作战武器的整体作战效能。
敏感性分析分为局部敏感性分析和全局敏感性分析[2]。局部敏感性分析通过改变模型中某个参数的取值,同时固定其他参数的取值,来探索模型响应的变化。但是局部敏感性分析不能计算变量间的交互作用对输出结果的影响。基于此,克服这些问题的全局敏感性分析得到广泛应用。全局敏感性分析[3-4]方法包括回归分析法、傅里叶振幅敏感性检验法、响应曲面法、互信息指数法、Sobol指数法等,其中Sobol指数法综合性能更好。
全局敏感性分析方法多用于气候、动力学方向的研究,Nossent等人[5]为评估复杂环境模型中参数的重要度,采用Sobol指数全局敏感性分析,产生复杂环境模型参数使用的关键信息。Zhang等人[6]使用基于方差的Sobol灵敏度分析,以中国河流流域为例,分析了干旱、正常、潮湿年份SWAT中参数的敏感性,从分析获得的结果中,加深了对土壤水分评估工具(SWAT)中敏感性参数的理解及不同指标和气候条件下的潜在水文过程。Mathieu等人[7]则将Sobol指数法应用在简化功能性结构植物模型中的参数,用于增强冬季油菜生长的研究。
传统Sobol指数敏感性分析采用蒙特卡洛方法计算敏感系数,需要大量的数据样本。如果只单纯依靠原复杂模型生成这些样本,计算成本过高。为此,可以采用代理模型替代原模型生成样本,节省计算时间,降低计算成本。目前,很多学者对代理模型进行了相关研究。Zhan等人[8]将多变量选择适应回归样条(MARS)作为分布式时变增益模型(DTVGM)的代理模型,进行参数敏感性分析。孔凡哲等人[9]将支持向量回归(SVR)引入水文模型构建代理模型,快速有效地定量评估参数敏感性,识别水文模型的关键参数。Luo等人[10]分别用径向基人工神经网络(RBFANN)与Kriging模型作为代理函数,在三氯乙烯(TCE)污染含水层上进行Sobol敏感性分析,以评估水井的修复时间、表面活性剂浓度和注射速率等设计变量对修复效率的敏感性。
当前基于代理模型的Sobol指数全局敏感性分析方法仍存在以下几个问题:1)代理模型存在拟合时间缓慢、拟合精度不高的问题。2)实验样本质量问题,首先是生成代理模型,需要大量的训练样本进行训练才能达到预订拟合精度;其次是Sobol指数法敏感系数的计算,传统蒙特卡洛抽样方法,收敛速度慢,计算量大。为此,本文针对第一个问题,引入拟合精度高、学习速度快的极限学习机[11]作为代理模型,构建一种基于极限学习机的全局灵敏度分析模型,并将该模型应用到武器装备作战效能的灵敏度分析。针对第二个问题,为减少代理模型所需样本数量,选择采样质量高的拉丁超立方体采样方法,提高拟合精度;同时为提高Sobol指数法计算效率,引入低差异、分布均匀的拟蒙特卡洛抽样方法代替蒙特卡洛抽样方法,减少抽样次数,提高收敛速度,降低计算成本。
1 基本方法与模型
1.1 作战效能评估模型
武器作战效能评估方法[12]繁多,主要包括试验统计法、解析法、作战模拟法和多指标综合评估法等。其中,解析法中的ADC模型[13]是美国工业界武器系统效能咨询委员会为美国空军而建立的,其评估模型为:
E(t)=A×D×C
(1)
其中,A=[a1,a2,a3,…,an]为系统的可用性向量,表示系统开始执行任务瞬间处于不同状态的概率。ai为开始执行任务时处于i状态的概率;D=(dij)n×n为可信性矩阵,dij表示开始瞬间系统处于i状态而在使用过程中转移到j状态的概率;C=(cjk)n×m为系统的能力矩阵,cjk表示在最后的可能状态j中达到的第k项效能指标值。利用ADC模型,能够合理地评估潜艇的作战效能,但是模型参数较多,计算复杂。
1.2 基于极限学习机的代理模型
代理模型可以对一组输入输出数据之间的关系用具体的数学表达式或数学模型表示。为精确拟合输入输出变量之间的关系,提高计算效率,本文引入极限学习机(ELM)作为代理模型,代替复杂的效能评估模型。ELM是一种单隐层的神经网络算法,ELM可以随机初始化输入权重和偏置并得到相应的输出权重。
假设有N个不同样本的训练集{(xi,oi)|xi∈Rn,ti∈Rm,i=1,…,N},其中输入样本xi=(xi1,xi2,…,xin)T,真实值oi。假设隐藏层含有K个节点,极限学习机[14]可以表示为:
(2)
式(2)中,xj为第j个样本输入;βi是第i个隐层节点与输出节点的输出权重;g(x)是隐层激活函数;ωi=(ωi1,ωi2,…,ωin)是第i隐层节点与输入节点之间的权重;bi是第i个隐层单元的偏置;tj为模型输出值。该网络模型可以用矩阵形式表示:
Hβ=T
(3)
其中,H是隐藏层节点输出矩阵:
H(ω1,…,ωL,b1,…,bL,x1,…,xL)=
该方法的学习目标是寻找最优权值,使得输出的误差最小。数学模型可表示为:
(4)
式(4)中,e表示模型输出值与真实值之间的误差,ej是第j个样本的模型输出值与真实值之间的误差。
单隐层的神经网络可以转化为求解一个线性模型的问题。由此确定输出权重:
(5)
1.3 实验设计
实验设计方法有很多,常见的经典采样法[15]有中心复合实验、全因子设计实验、正交设计实验等。这些采样方法,在多变量情况下,需要大量采样点才能获得可靠实验结果,计算成本高。拉丁超立方体采样法[16]采用等概率随机正交分布的原则,样本点的个数可以灵活设定,适用于多变量问题。所以本文在构建代理模型时,采用拉丁超立方体采样方法生成训练样本的输入变量集。拉丁超立方体采样点生成策略如下:
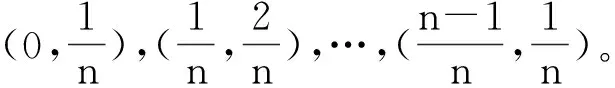
Sobol指数法敏感系数的计算,传统方法是通过蒙特卡洛抽样[17]实现,需要大量的实验样本,收敛速度慢,计算时间长。为有效减少试验次数,提高计算准确性,采用低差异、分布均匀的拟蒙特卡洛方法。常见的拟蒙特卡洛采样方法有Halton序列、Hammersley序列、Sobol序列等。其中Sobol序列分布均匀且不受样本数量限制,可替代蒙特卡洛抽样进行敏感性分析[18-20]。Sobol序列采样点生成策略如下:
Sobol序列是基于一组直接数di构造的随机序列,设qi是小于2i的正奇数,则di=qi/2i。
di以及qi的生成需要借助系数只为0或1的简单多项式,可表示为:
f(x)=xp+a1xp-1+…+ap-1x+ap
(6)
式(6)中,p为多项式的度数,a1,a2,…,ap为多项式系数。对于i>p,由递推公式求得di:
di=a1di-1⊕a2di-2⊕…⊕apdi-p⊕⎣di-p/2p」
(7)
式(7)中,⊕表示二进制按位异或。对于qi,递推公式为:
qi=2a1qi-1⊕22a2qi-2⊕…⊕2papqi-p⊕qi-p
(8)
综合以上推理,可以利用公式(9)生成Sobol序列x1,x2,x3,…
xn=b1d1⊕b2d2⊕…
(9)
式(9)中,bi是n的二进制形式。
1.4 全局敏感度分析模型
Sobol指数法是由俄罗斯学者Sobol[21]提出,并以他的名字命名的一种基于方差分解的全局敏感性分析方法。其核心思想是方差分解,把模型以单参数及参数之间组合的方式表示,通过计算单个输入参数或输入参数集的方差对总输出方差的影响来分析参数的重要性以及参数之间的交互效应。
假设数学模型为Y=f(X),平方可积,分解为单个模型参数及参数之间相互作用的子项函数之和:
(10)
其中,X=(x1,x2,…,xn),xi属于n维单位立方体Hn,式(10)中一共含有2n个子项。如式(10)满足:

(11)
(12)
公式(10)两边对除xi以外的其他各项求积分得到:
(13)
公式(10)两边对除xi、xj以外的其他各项求积分可得:
(14)
以此类推,可以得到公式(10)中等式右边的各个分解函数。
基于以上条件,Sobol指数敏感性分析方法定义了偏方差和总方差,并通过偏方差占总方差的比率来表示模型参数及其交互作用对目标响应的影响程度,其中模型f(X)的总方差为:
(15)
各子项的偏方差Di1,i2,…,is为:
(16)
变量的敏感性指数Si1,i2,…,is为:
(17)
式(17)中,Si∈(0,1)表示参数xi的一阶敏感性指数,描述了参数xi对输出的贡献度。参数的一阶敏感性指数越大,它对输出值的影响越大。为描述参数的整体影响,即参数的一阶敏感性影响及其与其他所有参数的交互影响对输出值的贡献度,引入了参数总敏感性影响指数[22]STi,总敏感性指数包含了变量之间的交互效应。若一个输入变量的全效应指数很小,表明该变量的变化不仅对输出影响小,而且与其他变量之间的交互效应也很小。因此,可以考虑对全效应指数小的变量取固定值,减少可变变量个数,从而简化模型。
根据文献[22],上述一阶敏感性指数可用公式(18)计算:
(18)
总敏感性指数:
(19)
2 武器装备作战效能敏感性分析
为解决基于ADC模型的作战效能评估存在的计算成本高、计算时间长的问题,本文提出基于极限学习机的武器装备作战效能全局敏感性分析模型,目的是找到影响作战效能的关键指标,进行功能完善与提高。模型计算流程如下:
算法1基于极限学习机的Sobol指数法
Step1明确作战任务,构建指标体系。
Step2采样设计,生成训练样本输入集,输入原效能模型,计算并输出训练样本结果集。
Step3训练样本集归一化处理。
Step4输入训练样本集,构建代理模型。
Step5采样设计,生成计算样本输入集并归一化,运行代理模型,输出计算样本结果集。
Step6计算样本集反归一化处理,利用Sobol指数敏感性分析,筛选敏感指标。
Step7根据敏感指标找到对应作战武器装备,对其进行功能优化。
算法1各步骤说明如下:
Step1针对潜艇具体作战任务,构建潜艇作战效能评估模型及其指标体系,效能评估模型为ADC模型。
Step2确定各指标的取值范围,采用拉丁超立方体采样方法生成N组训练样本输入变量,通过公式(1)计算出相应的效能值,得到N组训练样本集。
Step3进行样本预处理,对效能指标进行无量纲化处理,将样本值归一化到[0,1]。归一化公式为:
(20)
Step4生成代理模型,利用生成的训练样本集代入公式(4)训练极限学习机,拟合精度达到预先设定值,训练结束。代理模型拟合优度用均方误差(MES)和平均绝对误差(MAE)来衡量,值越小,预测结果越好。其中yi表示真实值,yi′为预测值,n为样本个数。
均方误差计算公式:
(21)
平均绝对误差计算公式:
(22)
Step5进行敏感性分析,利用拟蒙特卡洛方法中的Sobol序列,根据公式(6)~公式(9)生成计算样本输入集,由公式(20)归一化,通过代理模型计算效能值,生成计算样本集,进行反归一化处理,得到敏感性分析数据。
Step6根据公式(18)~公式(19)计算每个指标的一阶敏感性系数及总体敏感性系数。
Step7筛选出影响武器装备作战效能的敏感性指标,找到该指标对应的性能指标,进而得到影响武器效能的关键装备。
3 实例分析
本章包含2个实验,实例1为潜艇攻击海面舰艇的实例,将极限学习机作为代理模型进行敏感性分析,并与BP代理模型、SVR代理模型对比,证明方法的可行性和有效性。实例2为方法的应用,将本文提出的方法应用到新的案例中,验证方法的可用性。
3.1 实例1
实例1将潜艇作战系统划分为潜艇平台系统和武器系统这2部分,每个系统的初始状态分为故障和正常2种。本例构建潜艇作战能力评估指标如图1所示。

图1 潜艇作战效能评估指标
潜艇效能评估ADC模型中,能力矩阵C是各指标综合计算的结果,本例以潜艇各系统正常状态工作下的作战效能为例进行敏感性分析。由于效能指标多,本实验选取火力打击能力为敏感性分析的目标,其中,武器类型取值为离散型数值,分别为1、2、3,对应3种不同的武器类型。剩余5个子指标,如表1所示。根据每个指标的属性,确定取值范围。
表1 火力打击能力子指标

指标取值范围最小值最大值发射速度/(km·h-1)50120射程距离/km60110制导精度/°140武器数量/个310毁伤半径/m1050
实验采用基于拉丁超立方体采样的ELM代理模型(L-ELM)、BP代理模型(L-BP)、SVR代理模型(L-SVR)进行对比试验。隐层神经元个数为20,激活函数设置为sigmoid函数。训练样本选取样本集的90%,测试样本为样本集的10%。样本集设定为300个,分别运行3种代理模型。
表2 实例1代理模型实验结果与真实值对比
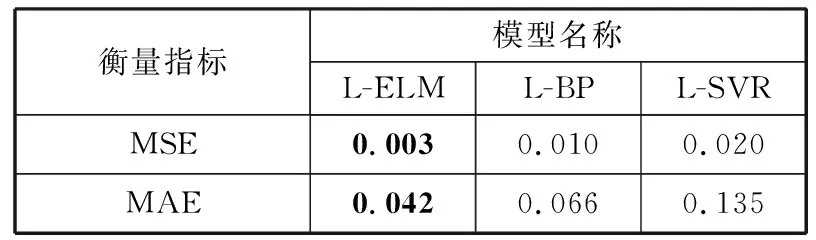
衡量指标模型名称L-ELML-BPL-SVRMSE0.0030.0100.020MAE0.0420.0660.135
由表2可知,3种代理模型分别对测试样本运算,结果与真实结果相比,其中L-ELM模型的MSE值、MAE值最小,说明L-ELM代理模型的拟合度最优。
图2为3种代理模型测试样本值与真实样本值拟合效果图。ADC曲线为真实效能值,从图中可以看出,L-ELM代理模型拟合效果优于L-BP模型、L-SVR模型,拟合效果最好。

图2 代理模型与真实模型效能值对比
图3为3种代理模型计算不同样本数量所用的时间,样本数量取[10,100,1000,10000,100000]进行测试,当样本数量超过10000时,L-BP模型与L-SVR模型运行时间变慢,L-ELM模型速度保持基本不变。
潜艇效能敏感性分析,设置3组对比试验与真实敏感系数进行对比,抽样方法为低差异的Sobol序列,设置样本数为10000。对比试验为:1)基于L-BP模型的敏感性分析;2)基于L-ELM模型的敏感性分析;3)基于L-SVR模型的敏感性分析。实验结果如表3所示。

图3 测试时间对比图
表3 火力打击能力指标敏感系数
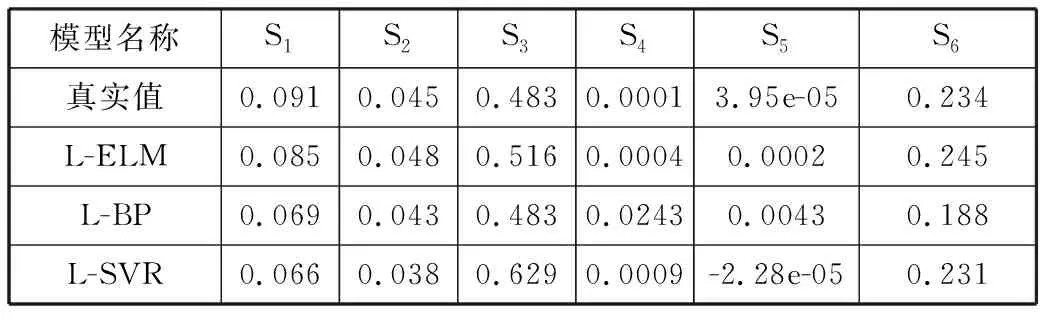
模型名称S1S2S3S4S5S6真实值0.0910.0450.4830.00013.95e-050.234L-ELM0.0850.0480.5160.00040.00020.245L-BP0.0690.0430.4830.02430.00430.188L-SVR0.0660.0380.6290.0009-2.28e-050.231
由表3可知,基于L-ELM模型计算的敏感性系数整体与真实的敏感性系数非常接近且稳定,而基于L-BP模型与L-SVR模型计算的敏感性系数不稳定,有些与真实值非常接近,如L-BP模型中敏感系数S3,L-SVR模型中S6与真实值非常接近,但有些偏离过大,如L-BP模型中S4、S5,L-SVR模型中S1、S3。
表4为火力打击能力指标的总敏感系数,可以看出,基于L-ELM代理模型计算得到的总敏感系数与真实值更接近,整体效果较好,而基于L-BP模型、L-SVR模型计算得到的总敏感系数与真实值差别较大,尤其是St4和St5与真实值差别明显。
表4 火力打击能力指标总敏感系数
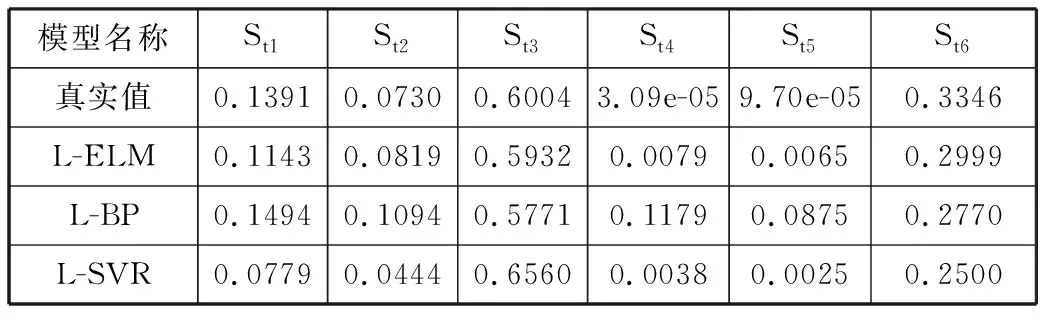
模型名称St1St2St3St4St5St6真实值0.13910.07300.60043.09e-059.70e-050.3346L-ELM0.11430.08190.59320.00790.00650.2999L-BP0.14940.10940.57710.11790.08750.2770L-SVR0.07790.04440.65600.00380.00250.2500
根据表3敏感系数Si从大到小排序S3>S6>S1>S2>S4>S5,得到影响火力打击能力的指标从强到弱依次为制导精度、毁伤半径、发射速度、射程距离、武器类型、武器数量。根据表4总敏感系数Sti从大到小排序St3>St6>St1>St2>St5>St4,得到火力打击能力指标间相互影响程度从强到弱依次为制导精度、毁伤半径、发射速度、射程距离、武器数量、武器类型。分析发现,制导精度、毁伤半径、发射速度是火力打击能力的关键因素,可以通过提高其相应的设备来提高火力打击能力。而射程距离、武器数量、武器类型自身的变化对效能值的影响较小,且对其他效能指标影响较小,所以在效能优化中,其值可以设定为固定值,减少计算成本及计算时间。
3.2 实例2
潜艇装备防空导弹对于空中威胁目标是十分必要的,在潜艇对空作战中,根据防空导弹装备体系的构成,作战能力划分为战场感知能力、指挥控制能力、火力打击能力,防空导弹效能值计算所需指标及取值范围如表5所示。
表5 防空导弹武器作战指标
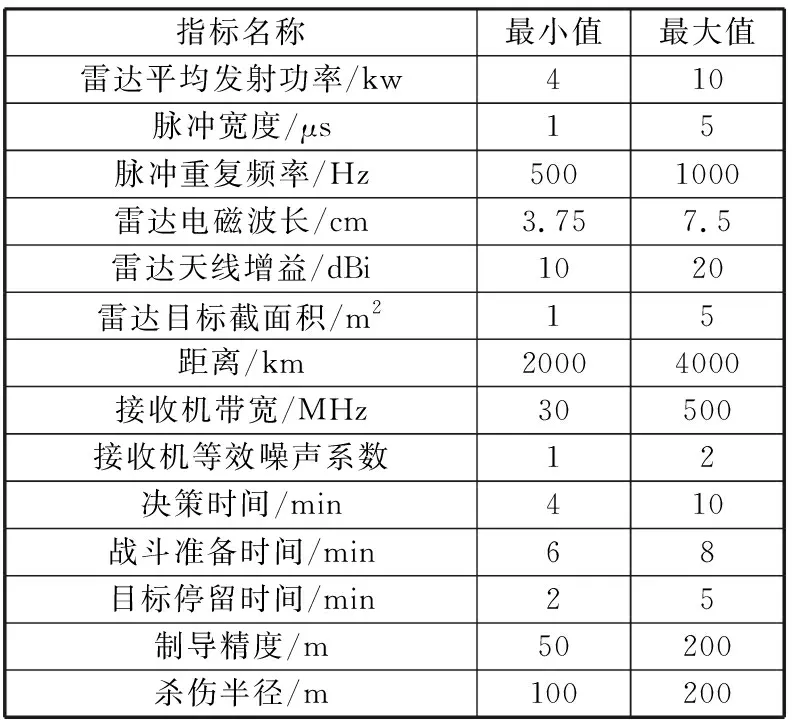
指标名称最小值最大值雷达平均发射功率/kw410脉冲宽度/μs15脉冲重复频率/Hz5001000雷达电磁波长/cm3.757.5雷达天线增益/dBi1020雷达目标截面积/m215距离/km20004000接收机带宽/MHz30500接收机等效噪声系数12决策时间/min410战斗准备时间/min68目标停留时间/min25制导精度/m50200杀伤半径/m100200
训练样本集设为1000,通过拉丁超立方体取样,将3种代理模型与真实模型仿真结果进行对比,结果如表6所示。由表6可知,L-EML模型计算结果与真实结果更加相近,拟合效果优于L-BP,L-SVR模型。
表6 实例2代理模型实验结果与真实值对比

评价指标模型名称L-ELML-BPL-SVRMSE0.00680.01070.0133MAE0.06350.08400.0981
防空导弹作战效能指标一阶敏感性分析结果、总敏感性分析结果分别如图4、图5所示。

图4 防空导弹作战效能指标一阶敏感性分析结果

图5 防空导弹作战效能指标总敏感性分析结果
从图4可以看出,影响防空导弹作战效能的指标敏感系数最大为雷达目标截面积S7,最小为决策时间S10、战斗准备时间S11。根据图4和图5分析对比,可以将总敏感系数小的指标设置为常数,表示它们的变化与其他指标间的相互影响较小,如决策时间St10、战斗准备时间St11、目标停留时间St3等,而雷达目标截面积S6、敌我距离S7、雷达电磁波长指标一阶敏感性指数与总敏感指数都很高,对提高防空导弹的效能影响较大,可以针对性地改进雷达中与其相关的装置,提高作战效能。
4 结束语
为提高武器装备的作战效能,通过全局敏感性分析找到影响作战效能的关键指标,引入ELM学习机可有效解决效能评估模型及仿真计算模型中计算成本高、时间长的问题。将本文方法与BP神经网、SVR支持向量回归模型进行对比,在计算精度相同的前提下,本文方法可节省大量计算时间。通过实例分析,基于ELM的全局敏感性分析方法分析得到的敏感系数合理,同时通过与真实结果的比对,验证了本方法的可行性,并且在样本数量极大的情况下,基于ELM的全局敏感性分析方法的时间消耗与其他算法相比,有明显的降低,使得在有限时间和预算内提升潜艇作战效能评估成为可能。
参考文献:
[1] 付东,方程,王震雷. 作战能力与作战效能评估方法研究[J]. 军事运筹与系统工程, 2006,20(4):35-39.
[2] Iooss B, Lemaitre P. A review on global sensitivity analysis methods[M]// Operations Research/ Computer Science Interfaces Series(Vol.59). Springer, 2014:101-122.
[3] 罗鹏程,傅攀峰. 武器装备敏感性分析方法综述[J]. 计算机工程与设计, 2008,29(21):5546-5549.
[4] 张晓航. 防空导弹武器装备体系作战效能全局敏感性分析方法研究[D]. 长沙:国防科学技术大学, 2010.
[5] Nossent J, Elsen P, Bauwens W. Sobol’ sensitivity analysis of a complex environmental model[J]. Environmental Modelling and Software, 2011,26(12):1515-1525.
[6] Zhang Chi, Chu Jinggang, Fu Guangtao. Sobol’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China[J]. Journal of Hydrology, 2013,480:58-68.
[7] Mathieu A, Vidal T, Jullien A, et al. Sensitivity analysis to help individual plant model parameterization for winter oilseed rape[C]// IEEE International Conference on Functional-Structural Plant Growth Modeling, Simulation, Visualization and Applications. 2017:133-139.
[8] Zhan Che-sheng, Song Xiao-meng, Xia Jun, et al. An efficient integrated approach for global sensitivity analysis of hydrological model parameters[J]. Environmental Modelling & Software, 2013,41(41):39-52.
[9] 孔凡哲,宋晓猛,占车生,等. 水文模型参数敏感性快速定量评估的RSMSobol方法[J]. 地理学报, 2011,66(9):1270-1280.
[10] Luo Jiannan, Lu Wenxi. Sobol’ sensitivity analysis of NAPL-contaminated aquifer remediation process based on multiple surrogates[J]. Computers & Geosciences, 2014,67:110-116.
[11] Huang Guang-bin, Zhu Qin-yu, Siew C K. Extreme learning machine: A new learning scheme of feedforward neural networks[C]// Proceedings of IEEE International Joint Conference on Neural Networks. 2004:985-990.
[12] 高尚,娄寿春. 武器系统效能评定方法综述[J]. 系统工程理论与实践, 1998,18(7):109-114.
[13] 吴晓锋,钱东. 用于系统效能分析的WSEIAC模型及其扩展[J]. 系统工程理论与实践, 2000,20(8):1-6.
[14] Ding Shifei, Zhao Han, Zhang Yanan, et al. Extreme learning machine: Algorithm, theory and applications[J]. Artificial Intelligence Review, 2015,44(1):103-115.
[15] 魏昕. 基于元模型的全局优化算法研究[D]. 武汉:华中科技大学, 2012.
[16] Mckay M D, Beckman R J, Conover W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 2000,42(1):55-61.
[17] Buslenko N P, Golenko D I, Sobol I M, et al.The Monte Carlo method[J]. Journal of the American Statistical Association, 1949,44(247):335-341.
[18] Sobol I M. On the distribution of points in a cube and the approximate evaluation of integrals[J]. USSR Computational Mathematics & Mathematical Physics, 1976,7(4):86-112.
[19] 周心莲. 几个常用随机数及其性质的比较[J]. 郧阳师范高等专科学校学报, 2010,30(6):13-17.
[20] Wang Chen, Duan Qingyun, Gong Wei, et al. An evaluation of adaptive surrogate modeling based optimization with two benchmark problems[J]. Environmental Modelling & Software, 2014,60(76):167-179.
[21] Sobol I M. Sensitivity estimates for nonlinear mathematical models[J]. Matem Mod, 1993,2(1):112-118.
[22] Paruggia M. Sensitivity analysis in practice: A guide to assessing scientific models[J]. Journal of the Royal Statistical Society, 2005,168(2):466.
