一种快速的双重层次包围盒碰撞检测算法
2018-06-04蒋夏军施慧彬
刘 超,蒋夏军,施慧彬
(南京航空航天大学计算机科学与技术学院,江苏 南京 211100)
0 引 言
碰撞检测作为计算机仿真领域的核心技术之一,是保证虚拟场景沉浸感、交互性以及构想性不可缺少的一部分。其主要作用是检测出虚拟场景中的物体之间是否发生穿透现象,从而避免破坏场景真实感。目前碰撞检测技术已经被广泛应用于机器人路径规划、计算机动画、虚拟装配以及计算机游戏等众多领域中,是计算机图形学领域的热点问题之一[1-2]。
针对这些领域的碰撞检测问题,学者们提出了许多不同类型的碰撞检测算法。从时间域角度划分,可以分为离散碰撞检测算法[3]和连续碰撞检测算法[4]这2类。前者在固定时间间隔对模型进行碰撞检测,后者一般采用线性插值的方法得到待测物体的运动轨迹方程,然后根据方程检测在整个时间区域内是否有碰撞发生。连续碰撞检测算法比离散碰撞检测算法精确度更高,但一般计算量过大,在实时性要求高的领域效果不如离散碰撞检测算法。从空间域角度划分,可以分为基于图像的碰撞检测算法[5]和基于图形的碰撞检测算法[6]。前者随着计算机硬件的发展是最近的研究热点,后者经过多年的发展,也出现了许多经典算法,基于层次包围盒的碰撞检测算法就是其中一种,目前被广泛应用于各类领域中。
本文主要研究基于图形域中的基于层次包围盒的碰撞检测算法,此类算法分为粗略碰撞检测和精确碰撞检测这2个阶段。它的核心思想是用常见的几何图形包围复杂的模型,排除大部分不相交的物体从而减少基本图元的相交测试,常见的包围盒主要分为轴向包围盒(AABB)[7]、有向包围盒(OBB)[8]、离散方向包围盒(K-Dop)[9]等几类。根据这些包围盒的特点,一些学者提出了基于混合包围盒的碰撞检测算法,这种算法分为2类,一类是层次包围盒,树上层节点和下层节点采用不同的包围盒[10];另外一类是层次包围盒,树的每个节点都包含2种不同的包围盒,外层的包围盒比内层的包围盒大,如K-DOP-Sphere[3]、OBB-sphere[6]等。但以上大部分算法中不同包围盒之间的相交测试是相互独立的,测试之间没有联系且并没有改进精确检测阶段中基本图元(三角形)之间的相交测试。
根据AABB简单的几何特性以及OBB的紧凑性,本文提出一种基于双层包围盒的碰撞检测算法。在此算法中,层次包围盒树的每个节点使用双层包围盒,外层使用特性简单的AABB,内层则使用OBB。在粗略碰撞检测阶段,本文将AABB之间的测试与OBB之间的测试联系在一起,简化OBB之间的相交测试;在基本图元相交测试阶段,利用OBB包围三角形的特点对基本图元之间的相交测试也进行优化。
1 构建双重层次包围盒
在基于层次包围盒的碰撞检测算法中,众多学者的研究成果表明,与其他多叉树结构相比较,二叉树的效率最高。因此本文算法中的层次包围盒树的结构也采用二叉树,一般有自顶向下、自底向上这2种方法构建层次包围盒树(BVH),本文选取自顶向下的方法,树的每个节点均包含2种包围盒。
1.1 计算方向包围盒
OBB是一个长方体,一般用一个中心点、一个旋转矩阵以及3个1/2边长来确定一个OBB。因为3条边方向的任意性,其计算方法相较于其他包围体也更为复杂,比较常用的方法是一种基于主成分分析法(PCA)计算最小OBB的方法,这种方法主要通过计算模型所有三角形顶点的均值和协方差矩阵C来确定OBB的中心点和方向,然后根据模型中所有三角形顶点在3条轴上的极值即可得到OBB的3条边长。
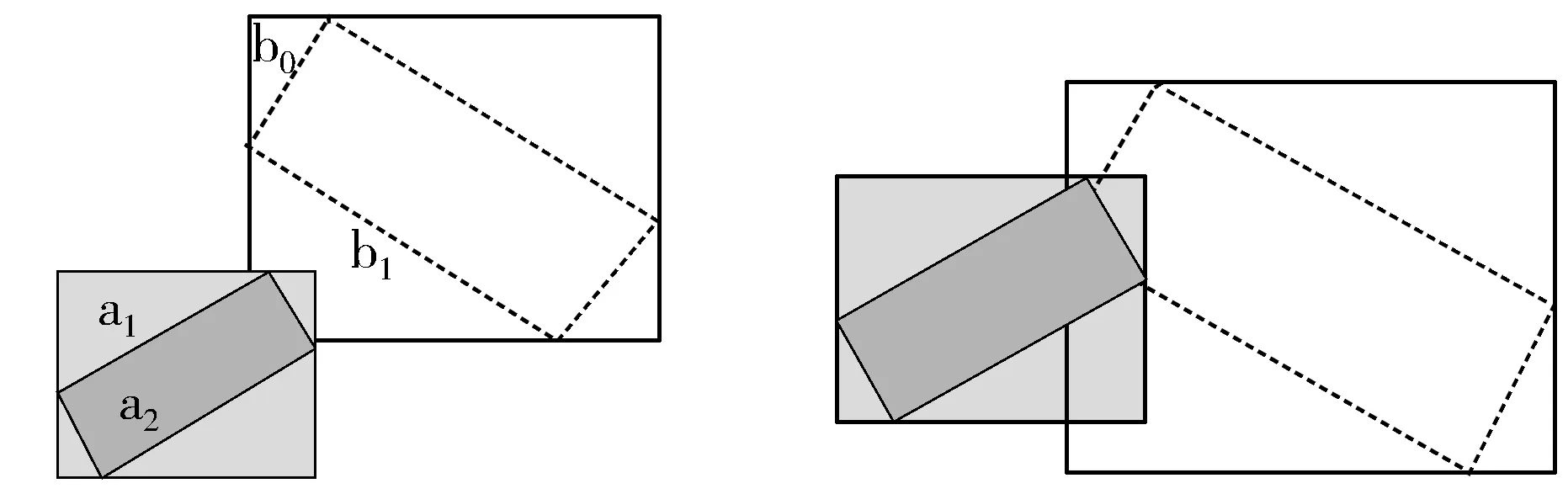
设给定的模型中有n个三角形(pk, qk, rk),其中0≤k mH,imH,j (1) 其中,ak和mk分别表示三角形k的面积和质心,i和j的值表示采取的坐标分量(x,y,z),例如,i的取值为1时则mk,i的取值为mk和x轴上的值。aH和mH分别表示模型的全面积和质心: 轴向包围盒AABB最大的特点就是3条边的方向与坐标轴的x、y、z轴平行,因此计算AABB时只需求得模型中三角形所有顶点在3条坐标轴上投影的最大最小值的顶点即可。在本文算法中,因为OBB与AABB的中点重合,可以直接根据已经求得的OBB方便快速地求得外层的AABB。 算法中的粗测阶段和常见的双层包围盒碰撞算法类似,首先对外层比较简单的AABB进行相交测试,若AABB之间相交,则继续对OBB之间进行测试,但与传统的分离轴测试方法不同的是,经过外层AABB测试过后,算法中的OBB之间的相交测试并不需要进行15条分离轴的测试,而只是检测特定的5条分离轴。 AABB之间的相交测试较为直观简单,因为3条边的方向均和坐标轴对齐,判断2个AABB之间是否相交,只需检测它们在3条坐标轴上是否相交,其中AABB在每一个坐标轴上的有效范围均可用相应坐标表示,因此只需比较对应的坐标值即可得到结果。 OBB之间的相交测试相较于AABB要复杂得多,一般采用一种基于分离轴理论(SAT)的方法,分离轴理论是分离超平面理论的扩展。分离超平面理论表明:任意2个给定的凸体,若凸体之间分离,则必定存在一个分离超平面使得2个凸体位于平面两侧。在实际应用中,一般使用垂直于此分离超平面的分离轴来判断凸体之间是否分离:对于一条给定的直线,若2个凸体在此直线上的投影不相交,则这条直线是它们的分离轴。2个OBB包围盒之间一共存在15条潜在的分离轴{a0,a1,a2,b0,b1,b2,c00,c01,c02,c10,c11,c12,c20,c21,c22},其中,ai和bi分别表示包围盒A和B的3条边的方向,下标值表示包围盒在此轴上的投影的大小关系,a0平行于包围盒A中最短的一条边,cij表示ai和bj的叉乘。 文献[7]指出cij在确定非相交结果时约占全部几率的15%,可以只对ai和bi共6条潜在的分离轴进行测试,但最终偏大的误报率加大了层次包围盒树的查询深度,最终的结果并没有达到预期的效果。在外层包围盒AABB相交的前提下,本文提出OBB之间的相交测试只需检测{a0,b0,c22,c12,c21}共5条潜在的分离轴的方案,下面给出此方案合理性的解释。 在对2个模型的层次包围盒树中的节点进行相交测试时,外层的AABB存在相交、分离这2种情况,若分离则不需要对内层的OBB进行测试;当结果相交时,对内层的OBB测试时也存在分离和相交2种情况,如图1所示。传统的分离轴测试方法通过检测全部15条潜在分离轴来区分图1中(a)和(b)的情况,而实际上在外层AABB相交的情况下,部分潜在分离轴确定OBB之间分离的优先级要远高于其他分离轴。图2表示AABB相交及OBB分离的3种情况,在保持相交分离情况不变的条件下,(a)(b)(c)中物体可移动的间距范围依次减小,因此在保持外层AABB相交的条件不变的情况下,物体相向移动则(a)(b)中的OBB分离的几率远大于图(c),在(a)(b)中,确定分离情况的分离轴皆平行于包围盒较短的边,即a0,b0。基于此,可以推测:在外层AABB包围盒相交的情况下,OBB在某条轴上的投影越小则此轴确定OBB之间分离的几率越大。 (a) AABB相交以及OBB分离 (b) AABB以及OBB均相交图1 AABB相交条件下OBB的2种位置关系 (a) 短轴确定OBB分离 (b) 长轴和短轴确定OBB分离 (c) 长轴确定OBB分离图2 AABB相交条件下OBB分离的3种情况 为了证明上述推论正确,引入包围盒的闵可夫斯基和[6]的概念,给定2个OBB包围盒A和B,它们的闵可夫斯基和A⊕B={a+b|a∈A,b∈B}是一个凸多面体,A∩B≠Ø(A和B相交)等价p∈A⊕B-p或q∈A⊕B-q。 证明:令A=A′+p,B=B′+q,p和q分别表示A和B的中心点,A′和B′分别由A和B中心平移至原点得到,则 A∩B≠Ø⟺(A′+p)∩(B′+q)≠Ø ⟺a+p=b+q(a∈A,b∈B) ⟺p=-a+b+q ⟺p∈A′⊕B′+q(A′关于原点对称) ⟺p∈(A-p)⊕(B-q)+q ⟺p∈A⊕B-p 根据上述结论,判断A和B是否相交,只需判断p(q)是否包含在沿向量-Op(-Oq)平移后的A和B的闵可夫斯基和内。 图3表明了在外层AABB相交的情况下,OBB之间的分离轴的优先级与包围盒在轴上的投影长度的关系。图3(a)表示物体A和物体B的包围盒,图3(b)中白色区域的多边形是(a)中的2个OBB的闵可夫斯基和,外面的矩形则为(a)中的AABB的闵可夫斯基和。由于图3(a)中AABB相交,因此物体A(B)的包围盒的中点(OBB和AABB中点重合)必定位于(b)中的矩形的某一点。当中点位于矩形中的白色区域时,a0、a1、b0、b1均不能作为OBB之间的分离轴,物体A和B的OBB之间相交;当中点位于矩形中的灰色区域时,a0或b0确定OBB之间分离;当中点位于黑色区域时,a1或b1为OBB之间的分离轴。根据图3(b)可知,黑色区域所占面积远远小于白色区域与灰色区域之和,因此可以确定在外层AABB相交的情况下,OBB在轴上的投影越小则此轴作为分离轴的可能性越大。 (a) (b)图3 物体A和B的包围盒以及包围盒的闵可夫斯基和 目前三维模型基本组成单元主要分为三角形或四边形,本文主要讨论由三角形构成的三维模型。在上文中,算法中的粗略碰撞测试阶段可以排除大部分不相交的三角形,但当模型之间的分离距离较小时,仍然需要对大量三角形对进行相交检测。 当前存在多种算法解决空间三角形之间的相交问题[12-15],其中Tropp算法和Devillers算法是其中比较典型、效率较高的2类测试算法,文献[15]对Tropp算法进行了改进并且取得了较好的效果。但由于模型中的三角形的坐标是基于其模型的局部坐标系,因此在使用以上算法对这些三角形之间测试时,需要将2个待测模型中的三角形转换到同一坐标系统。 设待测模型A和B在世界坐标系下的位置信息分别由旋转矩阵RA,RB和位移向量TA,TB表示,则将A中的三角形坐标变换到B所在的局部坐标系的公式为: TriA′=RBT·RA·TriA+RBT·(TA-TB) (2) 令RBA=RBT·RA,TBA=RBT·(TA-TB),根据公式(2),忽略RBA、TBA的计算步骤后一共还需要进行27次乘法运算以及27次加法运算,而大量的三角形的坐标变换运算无疑会影响整个算法的效率。根据单个三角形计算其OBB的过程,利用OBB之间相交测试所计算的中间值代替三角形的坐标值,可以省略以上的坐标变换步骤。 计算单个三角形的OBB步骤如下: 1)找出三角形最长的边作为OBB最长的1条边; 2)计算出三角形的法向量,法向量的方向与OBB最短的1条边的方向平行; 3)根据步骤1和步骤2的2条边计算出第3条边的方向。 由于三角形存在于一个平面,因此求得的OBB实际上是一个空间矩形,如图4所示,其中,l、d表示 图4 叶子节点OBB包围的三角形 矩形的长和宽,a是唯一需要额外计算的值,此计算可以在预处理阶段完成,且计算过程简单。在OBB相交检测阶段,已求得将2个矩形转换到同一坐标系统下的变换矩阵R[rx,ry,rz]以及平移向量T[t1,t2,t3],结合图4,则模型A和模型B中的三角形坐标可以用以下形式表示: A1=(l1,0,0),B1=rx·l2+T; A2=(a1,d1,0),B2=rx·a2+ry·d2+T; A3=(0,0,0),B3=T; 由于模型A中的三角形的坐标包含0值较多,以上坐标结合文献[15]的三角形相交检测算法实际上可以减少大量基本运算操作。最终整个三角形相交检测过程与文献[15]的原算法相比少了36次乘法操作、30次加法操作以及18次减法操作,文献[15]的算法一共需进行135~141次基本运算操作,而经过本文改进后只需要51~57次基本运算操作。 已知经典的RAPID碰撞检测软件包选用了OBB作为基本的包围盒,笔者通过修改RAPID包中包围盒测试阶段和三角形相交测试阶段的部分代码实现本文的算法。为了验证本文算法的效率,一共设计了2组实验,2组实验中的模型分别为佛像和汽车,如图5所示,实验开发平台为Microsoft Visual Studio 2010。 图5 佛像、汽车模型 图5佛像和汽车模型分别由125000个和152053个三角形构成。在实验中,分别验证了算法对不同距离下的模型进行碰撞检测时的效率,给定的距离分别为-2%、-1%、0%、1%、2%、3%,-2%表示2个模型之间相交且穿透距离为模型的轴向包围盒AABB最长边的2%,距离大于等于1%时表示模型之间分离。在解析模型时,对模型中的点坐标进行了缩放,使得模型外层AABB的包围盒最长边为固定的1,因此以上2%的距离实际上为0.02。对于以上每个特定距离,分别对模型进行38304次测试,在每次测试中均使用了不同的旋转矩阵、位移向量,这些矩阵向量由文献[16]中描述的算法产生,可以在网站http://cgvr.informatik.uni-bremen.de/research/colldet_benchmark/index.shtml下载得到。 本文算法分别与原RAPID碰撞测试包、QuickCD碰撞测试包以及Opcode碰撞测试包进行比较,其中QuickCD以及Opcode分别选用K-DOP包围盒和AABB包围盒,为了结果的公正性,将以上包围盒中三角形的相交测试算法均换成文献[15]提出的三角形检测算法,实验结果如表1所示。 表1 不同算法相交测试时间 单位:s 表1显示了4种算法对不同距离下的模型进行38304次碰撞检测的总时间,对比以上结果可知,本文算法比最快的Opcode效率高18%~25%,而比原RAPID算法快23%~30%,相比于最慢的QuickCD则快34%~52%。 在现存的基于层次包围盒的碰撞检测算法的基础上,本文提出了一种基于双层包围盒的碰撞检测算法,在算法的粗略检测阶段以及精确检测阶段都进行了有效优化,算法的效率相比于目前多种经典基于层次包围盒的碰撞检测算法都有比较显著的提升。本文算法可广泛应用于机器人路径规划、虚拟装配以及三维地表建模等众多领域。由于算法中层次包围盒树的叶子节点添加了额外的包围盒,因此相比于其他算法增加了算法的空间复杂度,在未来的工作中笔者将对算法的空间复杂度进行优化,并尝试将算法应用于变形仿真系统中。 参考文献: [1] 周清玲,刘艳,程天翔. 大规模柔体的连续碰撞检测算法[J]. 中国图象图形学报, 2016,21(7):901-912. [2] 李苗. 实时碰撞检测算法分析与比较[J]. 计算机与现代化, 2011(6):88-90. [3] Fang Zhigang, Jiang Jianxun, Xu Jie. Efficient collision detection using a dual K-DOP-Sphere bounding volume hierarchy[C]// International Forum on Information Technology and Applications. 2010:185-189. [4] 水泳. 虚拟现实中连续碰撞检测算法研究[D]. 合肥:中国科学技术大学, 2013. [5] 唐敏,林江,童若锋. 图形硬件加速的柔性物体连续碰撞检测[J]. 计算机学报, 2010,33(10):2022-2030. [6] Chang Jung-woo, Wang Wenping, Kim Myung-soo. Efficient collision detection using a dual OBB-sphere bounding volume hierarchy[J]. Computer Aided Design, 2010,42(1):50-57. [7] Van Den Bergen G. Efficient collision detection of complex deformable models using AABB trees[J]. Journal of Graphics Tools, 1997,2(4):1-13. [8] Gottschalk S, Lin M C, Manocha D.OBB-tree: A hierarchical structure for rapid interference detection[C]// Proceedings of the 23rd ACM Annual Conference on Computer Graphics and Interactive Techniques. 1996:171-180. [9] Klosowski J T, Held M, Mitchell J S B, et al. Efficient collision detection using bounding volume hierarchies of k-DOPs[J]. Transactions on Visualization and Computer Graphics, 1998,4(1):21-36. [10] 陈琳,戴骏,冯俊杰,等. 基于混合包围体层次树的机器人碰撞检测试验[J]. 武汉理工大学学报, 2014,36(2):125-130. [11] Ericson C. 实时碰撞检测算法技术[M]. 刘天慧译. 北京:清华大学出版社, 2010. [12] 赵景昌,白润才,刘光伟,等. 基于空间索引与碰撞检测的TIN求交算法[J]. 计算机工程, 2014,40(12):296-301. [13] Tropp O, Tal A, Shimshoni I. A fast triangle to triangle intersection test for collision detection[J]. Computer Animation and Virtual Worlds, 2006,17(5):527-535. [14] Guigue P, Devillers O. Fast and robust triangle-triangle overlap test using orientation predicates[J]. Journal of Graphics Tools, 2003,8(1):25-42. [15] Wei Ling-yu. A faster triangle-to-triangle intersection test algorithm[J]. Computer Animation and Virtual Worlds, 2014,25(5-6):553-559. [16] Trenkel S, Weller R, Zachmann G. A benchmarking suite for static collision detection algorithms[C]// International Conference in Central Europe on Computer Graphics, Visualization & Computer Vision. 2007:265-270.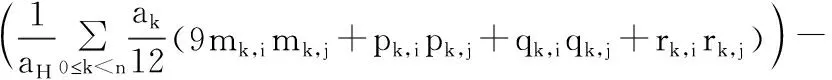
1.2 计算轴向包围盒
2 双重层次包围盒的相交测试
2.1 轴向包围盒相交测试
2.2 方向包围盒OBB相交测试



3 基本图元的相交测试

4 算法分析


5 结束语
