圆端形椭圆钢管混凝土受扭性能数值分析及抗扭承载力计算

王静峰，於忠华，沈奇罕，江 汉

(1. 合肥工业大学 土木与水利工程学院，安徽 合肥 230009； 2. 合肥工业大学 安徽土木工程结构和材料省级重点实验室，安徽 合肥 230009)

0引 言

钢管混凝土具有延性好、承载力高、抗震性能优越、施工便捷等优点。圆端形椭圆截面是钢管混凝土中新型截面形式之一，具有主轴抗侧刚度大、流体阻力系数小等优点，并具有独特的建筑美学效果，可提高建筑的舒适安全性，正逐步应用于桥梁工程和公共建筑中，例如宝鸡渭河大桥的拱肋、厦门杏林湾路段平台桥墩、武汉市后湖斜拉桥的塔柱等。

目前国内外仅少数学者进行了圆端形椭圆钢管混凝土柱轴压、偏压性能试验研究和数值分析。文献[1]～[3]进行了圆端形椭圆钢管混凝土短柱轴压、偏压试验。文献[4]～[7]通过数值分析研究了圆端形椭圆钢管混凝土短柱轴压、偏压性能。文献[8]通过数值分析研究了圆端形椭圆钢管混凝土长柱偏压性能和破坏模式。然而，目前国内外对圆端形椭圆钢管混凝土研究主要集中在轴压和偏压性能方面，缺少对其受扭性能的研究，且核心混凝土本构关系模型仍不明确。在实际工程中，圆端形椭圆钢管混凝土桥墩应用于跨河桥梁、城市高架桥和曲线梁桥时，在轮船、重型车辆偏心撞击和地震作用下会有严重的扭转效应[9-11]。框架结构的圆端形椭圆钢管混凝土框架角柱在水平地震力作用下也会受扭转效应的影响，因此有必要研究其受扭问题。

为了深入研究圆端形椭圆钢管混凝土构件核心混凝土的本构关系模型和受扭性能，本文提出了一种简单实用的圆端形核心混凝土本构关系等效方法。采用ABAQUS软件建立了纯扭作用下圆端形椭圆钢管混凝土构件的有限元模型，探究了钢材强度、混凝土强度、含钢率、长短轴比和截面面积等参数对圆端形椭圆钢管混凝土受扭性能的影响，分析了其在纯扭作用下的破坏模式，提出了受扭承载力计算公式。研究成果将为圆端形椭圆钢管混凝土的设计和应用提供科学依据。

1本构关系模型

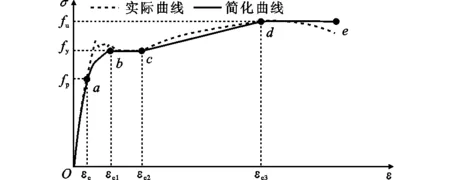
圆端形椭圆钢管混凝土截面如图1所示，其中t为钢管壁厚，DL为长轴长度，DS为短轴长度。武汉市后湖斜拉桥的塔柱如图2所示。钢材本构关系模型采用二次塑流模型[12]，其应力-应变(σ-ε)关系曲线如图3所示，曲线分为弹性段(Oa)、弹塑性段(ab)、塑性段(bc)、强化段(cd)和二次塑流(de)5个阶段。图3中fp,fy,fu分别为钢材的比例极限、屈服强度和极限抗拉强度，Es为钢材弹性模量，εe，εe1，εe2，εe3为应变特征值，εe=0.8fy/Es，εe1=1.5εe，εe2=10εe1，εe3=100εe1。

目前关于圆端形椭圆钢管核心混凝土本构关系模型的研究较少，根据其截面特性和相关研究[13-15]，本文提出了一种新等效计算方法。该等效方法按面积等同、含钢率不变的原则，将圆端形椭圆截面分别等效成圆形和矩形截面，如图4所示。等效后核心混凝土的本构关系模型按文献[16]进行计算。等效

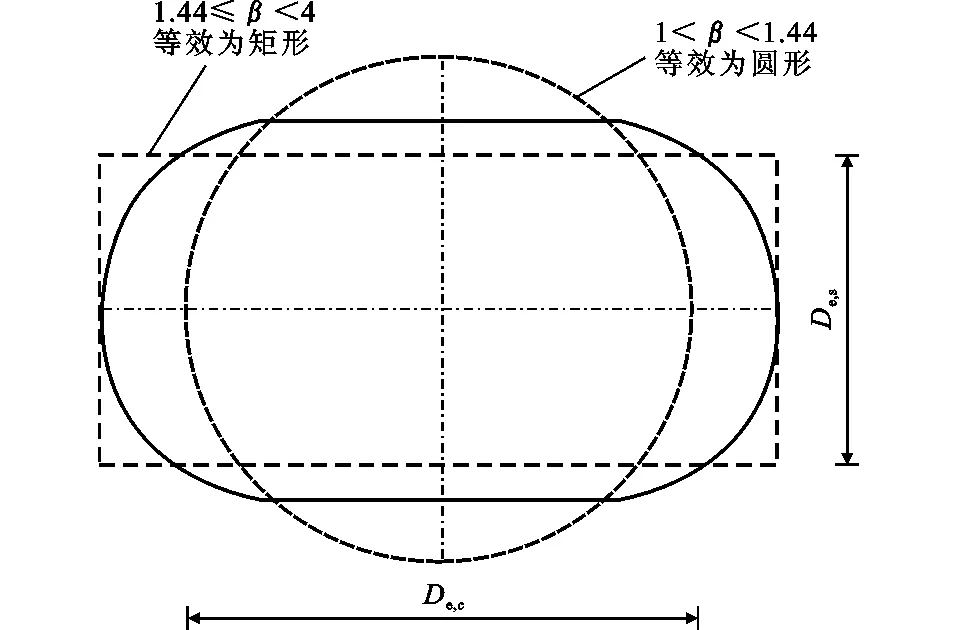
公式表达如下

(1)

式中：De为等效矩形短边长De,s或等效圆形直径De,c；β为圆端形椭圆截面长短轴比，介于1～4。

根据文献[17]的研究结果，等效后核心混凝土本构关系表达如下

(2)

x=ε/ε0,y=σ/σ0,σ0=fc

ε0=εc+800ξ0.2

εc=1 300+12.5fc

(3)

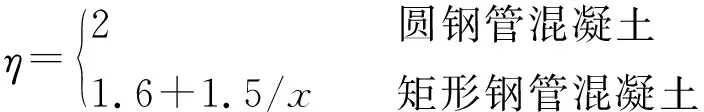
(4)

式中：ε0为峰值应变；σ0为峰值应力；ξ为约束效应系数；fc为混凝土轴心抗压强度；εc为混凝土相应于轴心抗压强度fc的应变；η为与截面形式有关的系数。

将约束效应系数ξ代入公式(2)中即可得出核心混凝土的本构关系模型。

2圆端形椭圆钢管混凝土受扭数值分析模型

采用ABAQUS建立了圆端形椭圆钢管混凝土构件受扭有限元分析模型，明确了核心混凝土和钢材本构关系、单元选取、网格划分、边界条件与复杂接触等。

2.1单元类型、荷载和边界条件

外钢管、核心混凝土和上下盖板均采用ABAQUS中的三维实体单元C3D8R进行模拟。核心混凝土和外钢管端面与上下盖板之间接触采用绑定约束，保证扭矩的传递。柱顶部为自由端，柱底部采用固接约束。建立参考点与上盖板耦合，对参考点施加转角位移实现扭矩，直至破坏。有限元分析模型见图5，其中U1，U2，U3分别为x，y，z方向的位移。

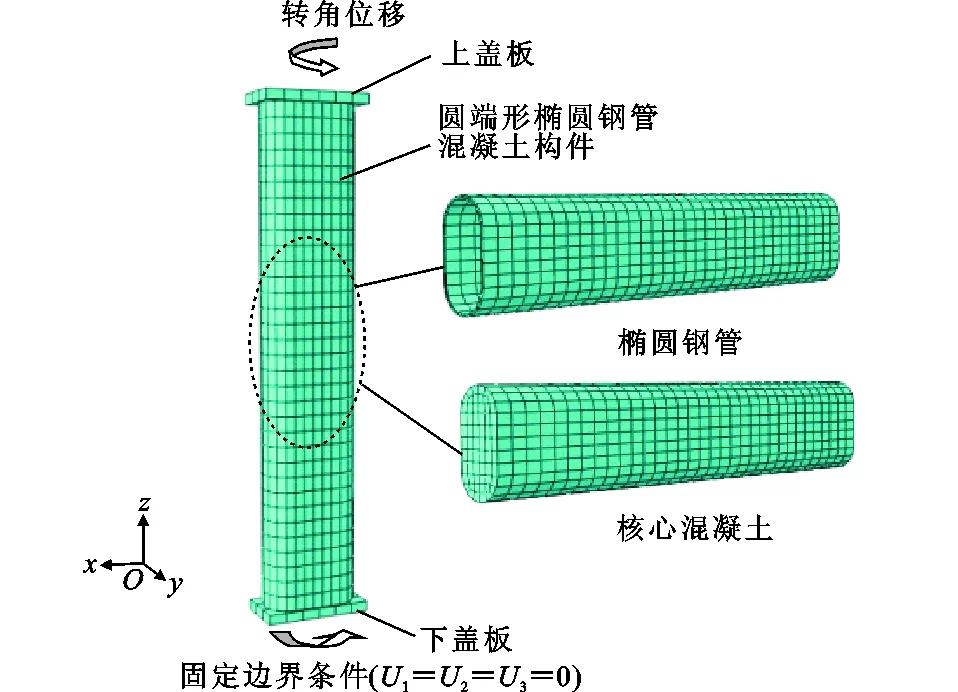
2.2相互作用

为考虑钢管和混凝土之间的接触问题，在ABAQUS中采用“表面与表面接触”的相互作用类型，切向行为定义成“罚”，法向行为定义成“硬接触”。

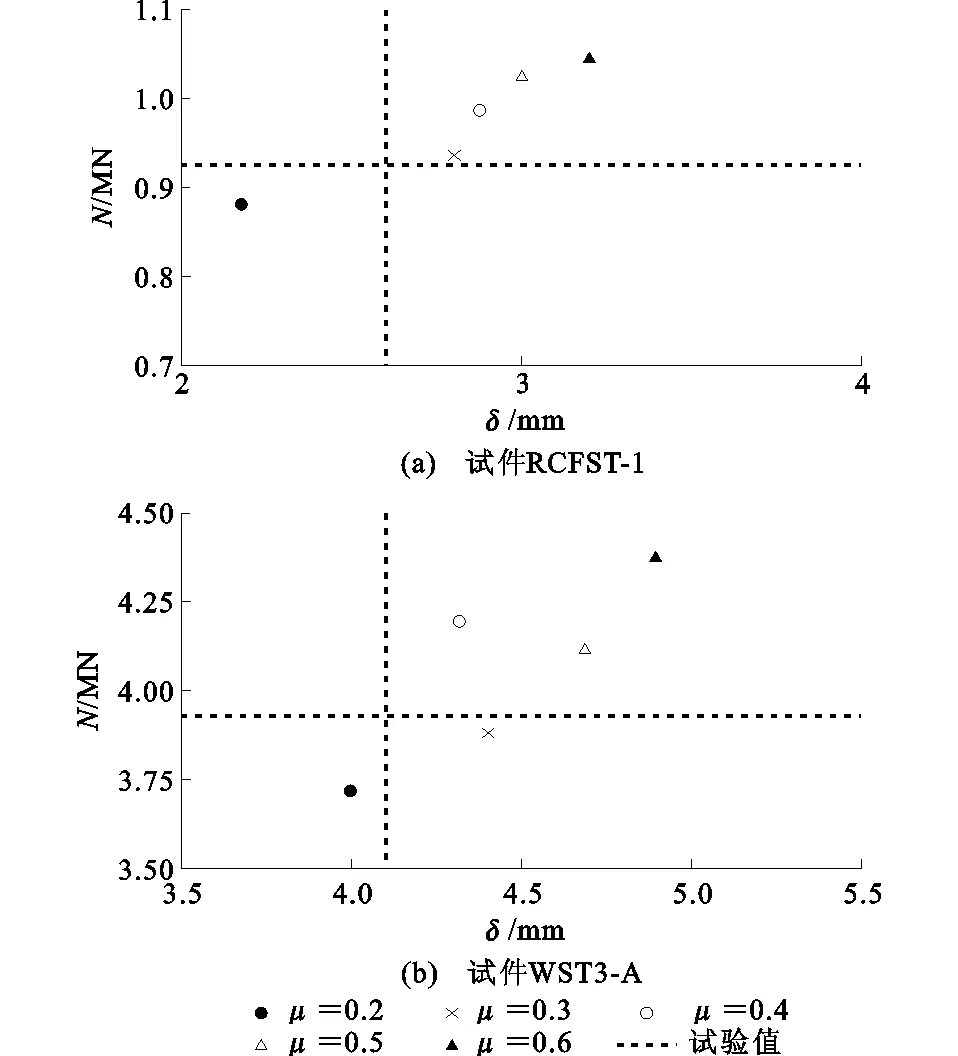
为考虑钢管和混凝土之间的相对滑移，本文分别对界面摩擦因数μ=0.2～0.6进行了探讨。图6给出了试验中圆端形椭圆钢管混凝土轴压短柱构件的峰值荷载N和峰值位移δ。由不同摩擦因数μ对应的有限元计算结果与试验结果[1-2]对比可知：随着μ的增大，有限元计算结果的峰值荷载N和峰值位移δ逐渐增大。当μ=0.3时，有限元计算结果与试验结果最为接近，故将摩擦因数设为0.3。

3试验验证

关于圆端形椭圆钢管混凝土构件受扭试验的研究较少，故采用圆、方钢管混凝土受扭试验数据来验证圆端形椭圆钢管混凝土受扭构件数值分析模型的准确性。

文献[18]进行了4根圆钢管混凝土构件受扭试验，验证了上下盖板与核心混凝土黏结良好无滑动，核心混凝土受纯扭作用。文献[19],[20]进行了方钢管混凝土构件受扭试验，均在上下盖板上焊接剪力钉嵌入核心混凝土，保证了核心混凝土受纯扭作用。试验中，试件的上盖板与加载装置相连，施加偏心力矩，试件受到扭矩作用。下盖板采用螺栓或地锚固定，作为固定端。因此，本文建立的有限元模型边界条件与试验试件的边界条件相符。

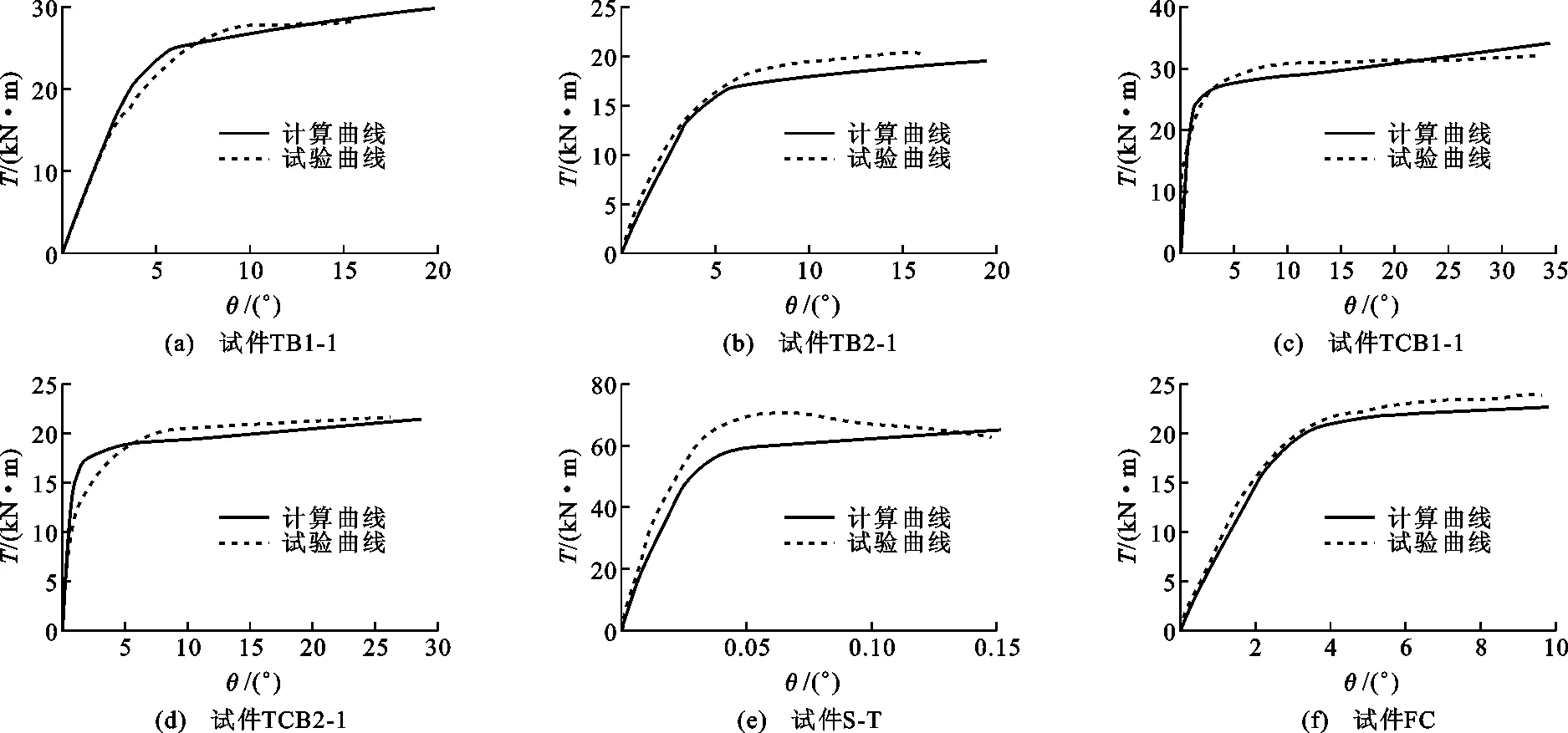
现将文献[18]～[20]中圆、方形钢管混凝土构件受扭试验的结果与数值分析结果进行比较，见表1和图7，图7中T为扭矩，θ为转角位移。圆端形椭圆钢管混凝土构件的扭矩-转角曲线没有明显峰值和下降段，文献[18]根据大量的研究发现，当构件试件FC和试件S-T为方形截面，其余试件为圆形截面。

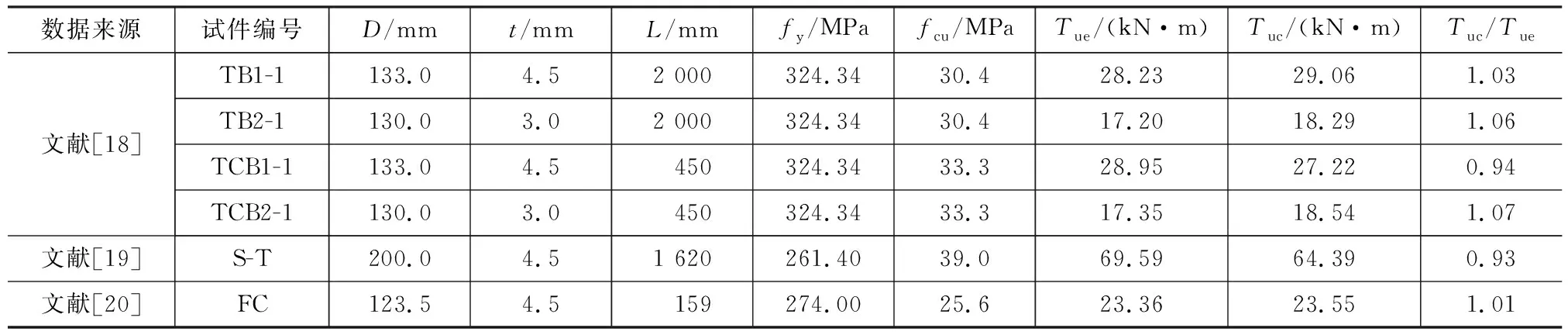
表1试验结果与有限元计算结果比较Tab.1Comparison of Test Results and Finite Element Calculation Results

注：D为圆管直径或方管边长；L为试件长度；fcu为混凝土立方体抗压强度；Tue为试件抗扭承载力试验值；Tuc为试件抗扭承载力计算值；

钢管最大剪应变达到10×10-3后，构件的扭矩-转角关系曲线趋向平缓，构件的转角位移增加较大，而扭矩增加较小。因此，本文定义圆端形椭圆钢管混凝土构件钢管最大剪应变为10×10-3时对应的扭矩为抗扭承载力。

结果表明，计算结果与文献[18]～[20]中的试验结果具有较高吻合度，且计算结果低于试验结果，较为安全。

4参数分析

本文分别研究钢材强度、混凝土强度、含钢率、长短轴比以及截面尺寸等参数对圆端形椭圆钢管混凝土构件抗扭承载力的影响。标准计算模型的参数设置为：钢材强度Q345，混凝土强度等级C50，含钢率α=0.16，长短轴比β=2，截面尺寸为200 mm×100 mm×5 mm。参数计算范围为：钢材强度Q235～Q630，混凝土强度C30～C80，长短轴比1≤β≤4，含钢率0.09≤α≤0.47，截面尺寸在120 mm×60 mm×3 mm～280 mm×140 mm×7 mm之间。为了深入分析圆端形椭圆钢管混凝土构件的受扭性能，引入含钢率α与约束效应系数ξ等参数。α，ξ的计算式分别为

α=As/Ac

(5)

(6)

式中：As为圆端形椭圆钢管截面面积；Ac为核心混凝土截面面积；fck为混凝土轴心抗压强度标准值。

4.1钢材强度

图8(a)给出了不同钢材屈服强度对圆端形椭圆钢管混凝土构件T-θ关系曲线的影响。与钢材强度Q345的试件作对比，Q235试件的抗扭承载力减小了35.3%， Q420和Q550试件的抗扭承载力分别增加了19.6%和62.9%。由此可见，随着钢材强度的增加，圆端形椭圆钢管混凝土构件的抗扭承载力会明显增大。

4.2混凝土强度

图8(b)给出了不同混凝土强度对圆端形椭圆钢管混凝土构件T-θ关系曲线的影响。混凝土强度C30试件的抗扭承载力比混凝土强度C50试件降低了10.5%，C80试件的抗扭承载力比C50试件只提高了2.8%。因此，混凝土强度对圆端形椭圆钢管混凝土的抗扭承载力几乎无影响。

4.3含钢率

图8(c)给出了不同含钢率对圆端形椭圆钢管混凝土构件T-θ关系曲线的影响。T-θ关系曲线弹性刚度随含钢率的增加而增加，抗扭承载力也会增加，曲线轮廓不变。与含钢率α=0.16的试件相比，α=0.09的试件抗扭承载力增加了42.2%，α=0.28和α=0.47的试件抗扭承载力分别提高了38.7%和90%。因此，含钢率对圆端形椭圆钢管混凝土构件的抗扭承载力影响较大。

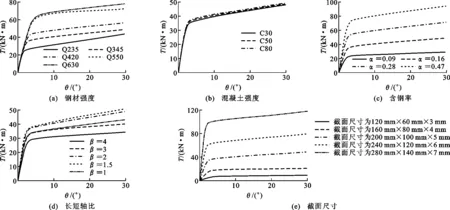
表2圆端形椭圆钢管混凝土受扭试件计算结果Tab.2Calculation Results of Circular-end Elliptical Concrete-filled Steel Tube Members Under Torsion

4.4长短轴比

图8(d)给出了不同长短轴比对圆端形椭圆钢管混凝土构件T-θ关系曲线的影响。随着β的增大，构件抗扭承载力不断增大。与β=2的试件相比，β=4，3，1的试件抗扭承载力分别下降23.3%，10.8%，10.5%；β=1.5的试件抗扭承载力提高了7.4%。可见圆端形椭圆钢管混凝土的抗扭承载力随着长短轴比β的减小而增大。当β<3时，圆端形椭圆钢管混凝土构件的抗扭承载力在相同含钢率条件下比圆形钢管混凝土构件大。

4.5截面尺寸

图8(e)给出了不同截面尺寸对圆端形椭圆钢管混凝土构件T-θ关系曲线的影响。与截面尺寸为200 mm×100 mm×5 mm的试件相比，截面尺寸为120 mm×60 mm×3 mm和160 mm×80 mm×4 mm的试件抗扭承载力分别降低了79%和51.9%，而截面尺寸为240 mm×120 mm×6 mm和280 mm×140 mm×7 mm的试件抗扭承载力分别提高了64.3%和153.4%。

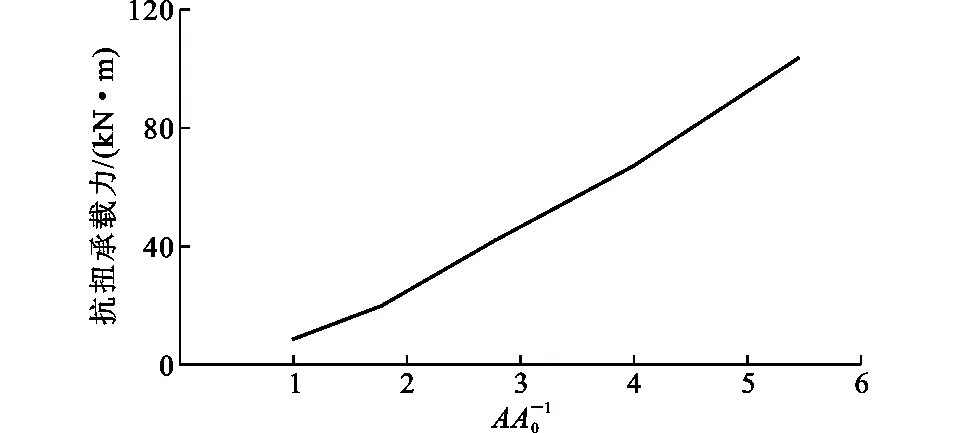
曲线弹性刚度和抗扭承载力会随着截面面积的增大而增大。图9为截面面积比与抗扭承载力关系曲线，其中A0为截面尺寸为120 mm×60 mm×3 mm试件的截面面积，A为其余4个截面的截面面积。由图9可知，圆端形椭圆钢管混凝土抗扭承载力与截面面积近似呈线性关系。

5受扭机理分析

圆端形椭圆钢管混凝土构件的T-θ关系曲线按其受力特点可分为3个阶段(图10)：

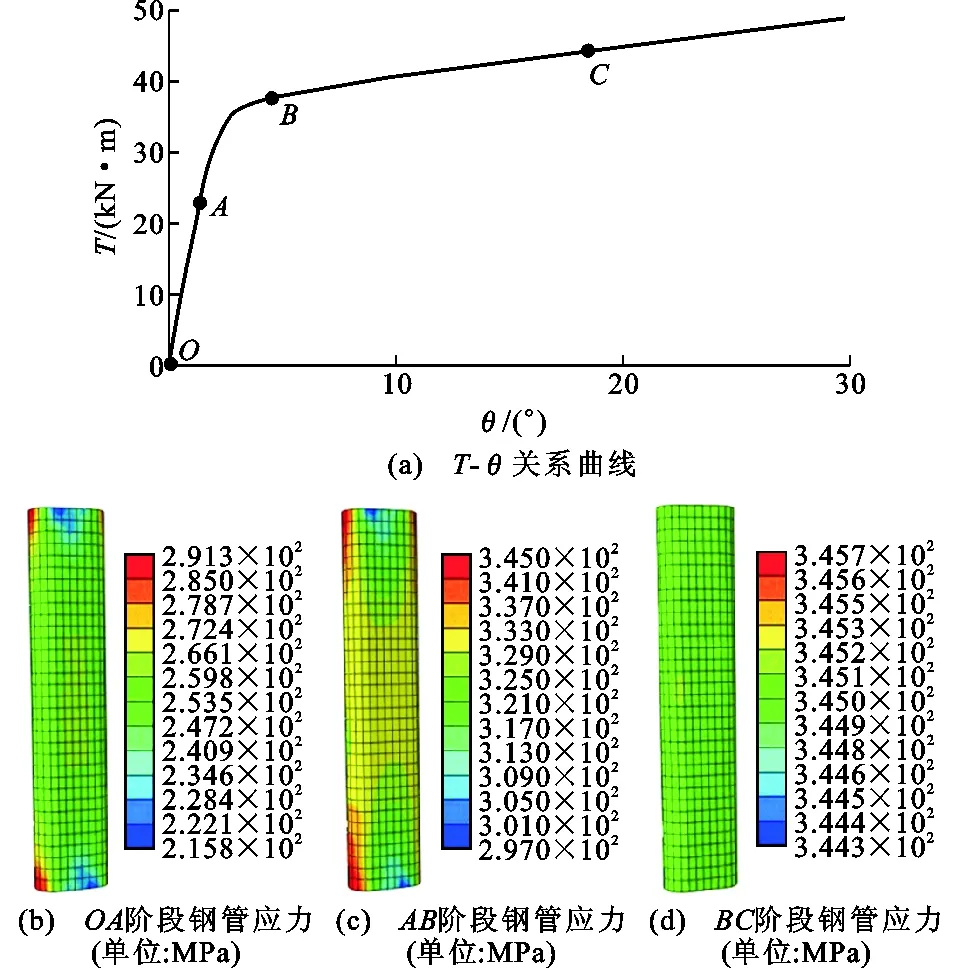
(1)弹性阶段(OA)。T-θ关系曲线为线性关系，钢管和混凝土应力处于弹性阶段，钢管和核心混凝土只在两端半圆弧上产生相互作用力。

(2)弹塑性阶段(AB)。钢管开始屈服，进入弹塑性阶段，核心混凝土在扭矩作用下裂缝逐渐开展，钢管和核心混凝土的相互作用力由两端半圆弧逐渐向两侧竖向钢管壁扩散。

(3)塑性强化阶段(BC)。钢管完全屈服，但混凝土有效阻止了钢管的凹屈，混凝土也由于外侧钢管的包裹而不会破坏。因此构件的抗扭承载力不断提高，表现出良好的塑性。

6抗扭承载力计算公式

目前中国外尚无圆端形椭圆钢管混凝土构件抗扭承载力Tu,pe计算公式的研究。圆端形椭圆钢管混凝土构件在扭矩作用下主要靠钢管承受扭矩，核心混凝土强度对抗扭承载力的提高很小，但内部混凝土能够有效防止圆端形椭圆钢管的内凹屈曲，从而提高圆端形椭圆钢管混凝土构件的整体塑性性能。在圆端形椭圆钢管混凝土构件整个抗扭过程中，当外钢管屈服后，外钢管短轴方向的竖直钢管壁和长轴方向的半圆弧相交处抗扭作用力最大，因此取相交处到圆端形椭圆圆心的距离为有效力臂r，如图11所示。忽略核心混凝土抵抗扭矩的作用，可得到如下计算公式

Tu,pe=Asfyr

(7)

(8)

式中：a′,b′分别为圆端形椭圆截面的长轴半径和短轴半径。

在实际计算中，考虑到圆端形椭圆长短轴比的影响以及部分截面发展塑性，对原公式进行折减，最后得出圆端形椭圆钢管混凝土构件抗扭承载力简化计算公式如下

Tu,pe=YTAsfyr

(9)

式中：YT为长短轴比折减系数，当β=1.5时，YT=0.7，当β=2时，YT=0.6，当β=4时，YT=0.28，中间按线性插值法取值。

公式(7)适用于Q235～Q630的钢材和C30～C80的混凝土，含钢率α=0.06～0.47、长短轴比β=1.5～4。由参数分析可知，圆端形椭圆钢管混凝土构件抗扭承载力的增大与截面面积的增加近似呈线性关系，因此公式(7)的适用范围不受截面面积制约。圆端形椭圆钢管混凝土构件抗扭承载力公式的计算结果与有限元计算结果比较见表3。

结果表明：有限元计算的抗扭承载力与计算公式得到的抗扭承载力吻合较好。因此，本文提出的圆端形椭圆钢管混凝土构件抗扭承载力简化计算公式较准确，且计算结果总体偏于安全。

7结语

(1)由于目前圆端形椭圆钢管核心混凝土本构关系仍不明确，本文提出了一种圆端形椭圆钢管核心混凝土本构关系的等效方法，并通过试验验证了等效方法的准确性与可行性。

(2)钢材强度、截面含钢率、长短轴比和截面尺寸为影响圆端形椭圆钢管混凝土构件受扭承载力的主要参数。钢材强度、截面尺寸和含钢率越大，长短轴比越小，构件受扭承载力越大。

(3)长短轴比β影响圆端形椭圆钢管混凝土钢管和混凝土之间的相互作用，随着β的降低，钢管对混凝土的约束逐渐加强，两者之间相互作用力的分布也更为均匀。

(4)圆端形椭圆钢管混凝土构件受扭可分为弹性阶段、弹塑性阶段和塑性强化阶段。在塑性强化阶段，扭矩增加趋于平缓，由此可见，圆端形椭圆钢管混凝土构件表现出较好的塑性性能。

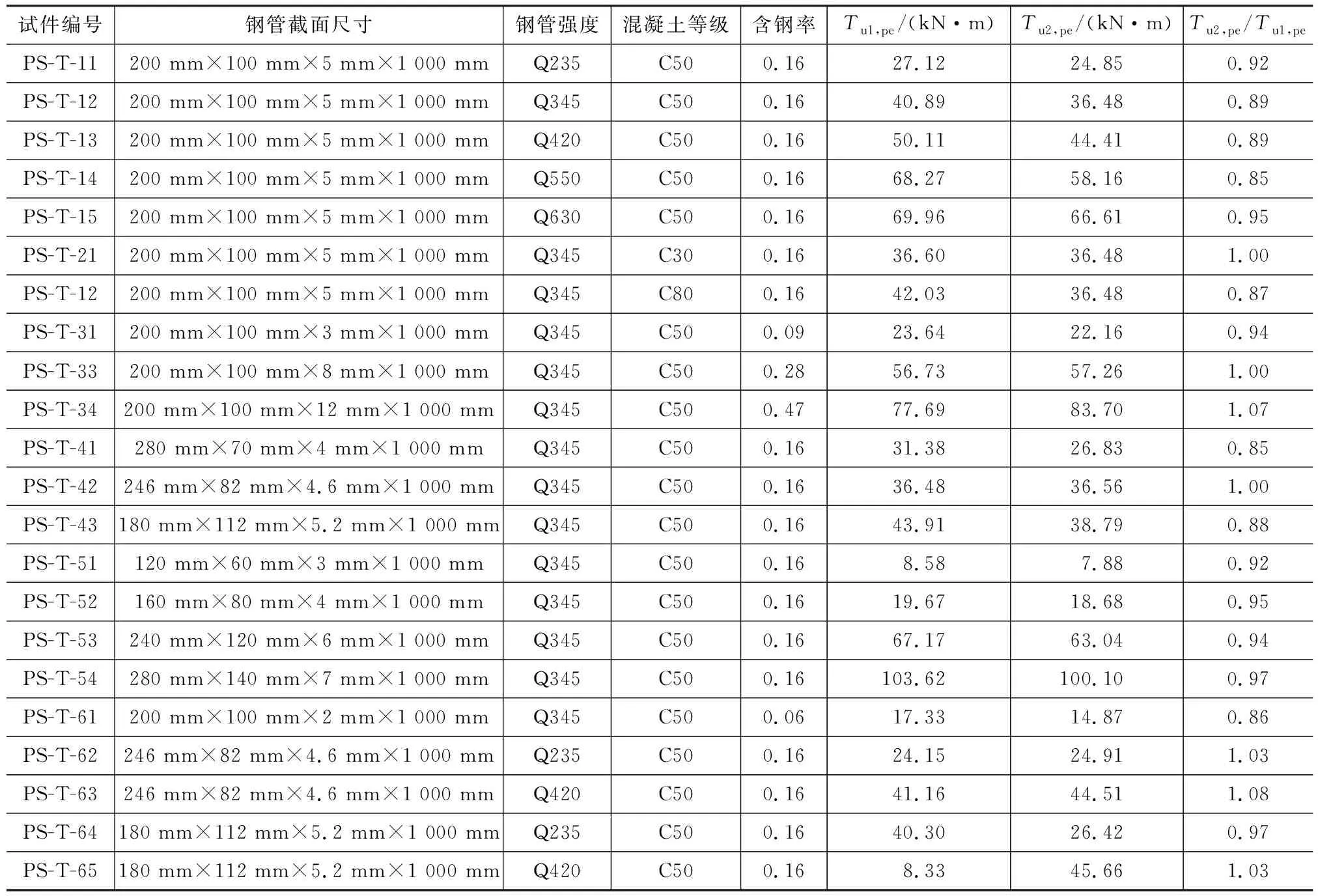
表3公式结果与有限元结果比较Tab.3Comparison Between Formula Results and Finite Element Results

注：Tu1,pe为扭矩有限元计算值；Tu2,pe为扭矩公式计算值。

(5)本文提出了圆端形椭圆钢管混凝土构件抗扭承载力的简化计算公式，并验证了公式的准确性与可靠性。研究成果可为建立圆端形椭圆钢管混凝土构件受扭设计方法提供参考依据。

参考文献：

References:

[1] 王志滨,陈 靖,谢恩普,等.圆端形钢管混凝土柱轴压性能研究[J].建筑结构学报,2014,35(7):123-130.

WANG Zhi-bin,CHEN Jing,XIE En-pu,et al.Behavior of Concrete-filled Round-end Steel Tubular Stub Columns Under Axial Compression[J].Journal of Building Structures,2014,35(7):123-130.

[2] 李 刚.新型钢-混凝土组合结构力学性能研究[D].长沙:中南大学,2012.

LI Gang.The Mechanical Behaviors of New Steel-concrete Composite Structure[D].Changsha:Central South University,2012.

[3] 谷利雄,丁发兴,付 磊,等.圆端形钢管混凝土轴压短柱受力性能研究[J].中国公路学报,2014,27(1):57-63.

GU Li-xiong,DING Fa-xing,FU Lei,et al.Mechanical Behavior of Concrete-filled Round-ended Steel Tubular Stub Columns Under Axial Load[J].China Journal of Highway and Transport,2014,27(1):57-63.

[4] DING F X,FU L,YU Z W,et al.Mechanical Performances of Concrete-filled Steel Tubular Stub Columns with Round Ends Under Axial Loading[J].Thin-walled Structures,2015,97:22-34.

[5] XIE J X,LU Z A.Numerical Simulation and Test Study on Non-uniform Area of Round-ended CFST Tubular Tower[C]//IEEE.Proceedings of 2010 Third International Conference on Information and Computing.Mumbai:IEEE,2010:19-22.

[6] 付 磊,丁发兴,谷利雄,等.圆端形钢管内约束混凝土轴压短柱的力学性能[J].华南理工大学学报:自然科学版,2014,42(11):113-120.

FU Lei,DING Fa-xing,GU Li-xiong,et al.Mechanical Properties of Stirrups Confinement Concrete-filled Round-ended Steel Tubular Stub Short Columns Under Axial Compression[J].Journal of South China University of Technology:Natural Science Edition,2014,42(11):113-120.

[7] 谢恩普,王志滨,林 盛,等.圆端形钢管混凝土轴压短柱的机理分析[J].福州大学学报:自然科学版,2015，43(4):517-522.

XIE En-pu,WANG Zhi-bin,LIN Sheng,et al.Mechanism Analysis on Concrete-filled Round-end Steel Tubular Stub Columns Under Axial Load[J].Journal of Fuzhou University:Natural Science Edition,2015,43(4):517-522.

[8] 李德山,池思源,王志滨.圆端形钢管混凝土柱偏压力学性能研究[J].福州大学学报:自然科学版,2016,44(4):538-542.

LI De-shan,CHI Si-yuan,WANG Zhi-bin.Mechanical Behavior of Round-end Concrete-filled Steel Tubular Columns Under Eccentric Load[J].Journal of Fuzhou University:Natural Science Edition,2016,44(4):538-542.

[9] 罗旗帜,徐中山,苏 成.船桥偏心碰撞的撞击力计算[J].公路交通科技:应用技术版,2010(11):313-316.

LUO Qi-zhi,XU Zhong-shan,SU Cheng.Calculation of Impact Force of Ship Bridge Eccentric Collision[J].Journal of Highway and Transportation Research and Development:Application Technology Edition,2010(11):313-316.

[10] 徐中山.船桥碰撞动力响应研究[D].广州:华南理工大学,2010.

XU Zhong-shan.Research on Dynamic Response of Ship Bridge Collision[D].Guangzhou:South China University of Technology,2010.

[11] 王宇航.曲线梁桥钢管混凝土桥墩的扭转效应研究[D].北京:清华大学,2013.

WANG Yu-hang.Study on Torsion Effect in Concrete Filled Steel Tube Piers of Curved Girder Bridges[D].Beijing:Tsinghua University,2013.

[12] 沈奇罕.椭圆钢管混凝土轴压、偏压和抗弯性能与破坏机理研究[D].合肥:合肥工业大学,2016.

SHEN Qi-han.Research on Behaviors and Failure Modes of Elliptical Concrete Filled Steel Tube Under Axial Compression,Eccentric Compression and Bending Moment[D].Hefei:Hefei University of Technology,2016.

[13] 宋顺龙,王静峰,江 汉,等.椭圆钢管混凝土受扭性能及抗扭承载力计算[J].合肥工业大学学报:自然科学版,2017,40(7):952-959.

SONG Shun-long,WANG Jing-feng,JIANG Han,et al.Torsional Behavior and Ultimate Torsional Strength Calculation of ECFST[J].Journal of Hefei University of Technology:Natural Science,2017,40(7):952-959.

[14] 沈奇罕,王静峰,王 伟,等.基于数值分析的椭圆钢管混凝土柱轴压性能及承载力计算[J].建筑钢结构进展,2015,17(6):68-78.

SHEN Qi-han,WANG Jing-feng,WANG Wei,et al.Axial Compressive Behavior and Bearing Capacity Calculation of ECFST Columns Based on Numerical Analysis[J].Progress in Steel Building Structures,2015,17(6):68-78.

[15] ZHAO X L,PACKER J A.Tests and Design of Concrete-filled Elliptical Hollow Section Stub Columns[J].Thin-walled Structures,2009,47(6/7):617-628.

[16] 韩林海.钢管混凝土结构——理论与实践[M].2版.北京:科学出版社,2007.

HAN Lin-hai.Concrete Filled Steel Tubular Structures — Theory and Practice[M].2nd ed.Beijing:Science Press,2007.

[17] 刘 威.钢管混凝土局部受压时的工作机理研究[D].福州:福州大学,2005.

LIU Wei.Research on Mechanism of Concrete-filled Steel Tubes Subjected to Local Compression[D].Fuzhou:Fuzhou University,2005.

[18] 韩林海,钟善桐.钢管混凝土纯扭转问题研究[J].工业建筑,1995,25(1):7-13.

HAN Lin-hai,ZHONG Shan-tong.The Studies of Pure Torsion Problem for Concrete Filled Steel Tube[J].Industrial Construction,1995,25(1):7-13.

[19] 陈逸玮.钢管混凝土柱形状因素与扭转韧性行为研究[D].桃园:中央大学,2003.

CHEN Yi-wei.Study on Form Factor and Torsional Toughness Behavior of Concrete Filled Steel Tubular Columns[D].Taoyuan:Central University,2003.

[20] KITADA T,NAKAI H.Experimental Study on Ultimate Strength of Concrete-filled Square Steel Short Members Subjected to Compression or Torsion[C]// ASCCS.Proceedings of the Third International Conference on Steel-concrete Composite Structures.Fukuoka:ASCCS,1991:137-142.