基于成都黏土蠕变试验的非定常蠕变本构模型研究

任 鹏，王 鹏,2，唐 印

(1. 四川省建筑科学研究院 四川省建筑工程质量检测中心，四川 成都 610036； 2. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

0引 言

经工程实践证明，黏土的变形不仅与所承受的荷载有关，还与荷载作用的时间有关，这表明黏土具有蠕变特性。在低应力水平时，黏土一般表现为瞬时弹性变形和衰减蠕变变形；在高应力水平时，黏土表现为加速蠕变变形。黏土的蠕变性常常给工程带来许多的问题，甚至造成重大损失，因此深入开展黏土蠕变特性的研究具有重要的意义和价值。

目前阶段，对黏土蠕变模型的研究大多采用元件模型，即通过弹簧元件、黏壶元件和摩擦元件串联、并联组成各种蠕变本构模型。传统的元件模型所建立的蠕变本构模型是一种整数阶的线性关系，很难准确描述黏土的非线性蠕变特性。为了描述黏土蠕变的非线性特性，有人利用元件模型和经验模型结合的方法来建立黏土的非线性蠕变本构方程。周秋娟等[1]对广州南沙软土进行了蠕变试验，并分析了预加荷载和不加荷载条件下固结试样对蠕变的影响，探讨了软土非线性流变变形的特性；李珍玉等[2]通过结合膨胀土的线性黏塑性模型和非线性黏塑性经验模型，建立了能够描述膨胀土的流变非线性黏塑性本构方程；肖宏彬等[3-6]通过压缩蠕变试验、应力松弛试验，探讨了膨胀土的蠕变特性，总结得出非饱和膨胀土的非线性经验蠕变模型。

非线性经验模型或半经验半理论模型往往具有模型复杂、参数多、区域性强等缺点。近年来，由于分数阶微积分的发展，不少人将其引入到黏土的蠕变本构模型中来，试图克服黏土非线性经验、半经验模型的缺点。殷德顺等[7-9]通过研究岩土材料的应力-应变关系，提出将分数阶微积分引入岩土流变模型，建立了一种新的流变模型元件(软体元件)，用于更准确地描述黏土加速蠕变阶段。在此基础上，更多学者[10-13]将分数阶微积分用来推导岩土体蠕变本构模型，所推导出的模型能够较好地描述岩土材料的瞬时蠕变、稳态蠕变和加速蠕变3个阶段；同时，经过拟合辨识分析，分数阶蠕变模型具有参数少、确定方法简单和适用性高等优点。

由于黏土的区域性强，本文紧密结合成都东区黏土的性质(具有弱—中膨胀性)，开展以下研究：

(1)进行成都黏土的常规三轴固结不排水试验和三轴固结不排水蠕变试验，分析成都黏土的偏应力、蠕变特性、长期强度、弹性模量和黏滞系数特性。

(2)根据成都黏土的蠕变特性，确定蠕变本构方程，并在方程中引入分数阶微积分理论；同时，确定蠕变本构方程中弹性模量和黏滞系数的非定常性。

(3)将成都黏土的蠕变本构方程与试验数据进行拟合和辨识分析，明确所推导的蠕变本构方程的合理性以及可靠性。

1常规三轴试验和蠕变试验

1.1试验仪器

本文试验仪器采用长春试验机研究所生产的CSS-2901TS土体三轴流变试验机(图1)。该试验机可以完成常规三轴固结不排水剪切试验和三轴蠕变试验，使用同一套仪器完成所有试验，可避免仪器对试验结果的影响。

1.2试验方法

常规三轴剪切试验和蠕变试验均在100 kPa围压下固结和剪切，固结过程中排水，剪切过程中不排水。

1.2.1试样采取及制备

本次试验从成都成华区八里庄采取黏土试样，风干、粉碎后过孔径2 mm的筛，首先完成基本土工试验，参数见表1。采用蒸馏水配置试样的天然含水率(28.2%)，并密封保存48 h以上；然后根据试样干密度和试样规格(直径为39.1 mm，高度为80 mm)确定单个制样器的装样质量；试样分4层击实，最后抽真空饱和试样48 h；一共制备3组试样，每组3个试样。

1.2.2常规三轴固结不排水试验

常规三轴固结不排水试验按以下步骤进行：

表1成都黏土的基本性能参数Tab.1Basic Property Parameters of Chengdu Clay

(1)将饱和后的试样安装在试验机上，检查无误后，设置围压从0 kPa加压到100 kPa，加压速率为0.1 kPa·min-1，直至加压完成。

(2)围压加压完成后，对试样进行固结。在固结过程中打开与试样相连的排水阀，以便试样固结排水，同时测量在固结期间所排水的体积和质量。

(3)根据CSS-2901TS试验机的特点，采用控制应变速率的方式剪切试样，设置剪切速率为0.08 mm·min-1，剪切试样直至试样破坏或变形量大于试样高度的20%(16 mm)即可。

(4)试验过程中采用计算机记录试验数据，设置数据记录时间间隔为12.5 min；根据《土工试验规程》(SL 237—1999)处理试验数据，并绘制轴向应力-应变曲线，得出成都黏土破坏偏应力qf。

1.2.3蠕变试验

蠕变试验按以下步骤进行：

(1)在检查试验仪器无误后开始装样，然后设置100 kPa的目标围压进行加压，加压速率为0.1 kPa·min-1，直至加压完成。

(2)固结试样，在固结过程中需要打开与试样相连的排水阀，并记录所排水的体积和质量。

(3)将固结完成后测得的轴向压力值作为蠕变试样的初始值。本次蠕变试验采用分级加载的方式，即根据破坏偏应力qf，可得每级轴向加载偏应力Δqf=qf/N，N为加载级数，本文取N=4。

(4)在每级轴向荷载加载完成，待试样轴向变形稳定后，开始加载下一级荷载，直至试样破坏。每级荷载稳定的标准为轴向变形量小于0.01 mm·d-1，若不能满足，继续本级试验，直至达到标准。

成都黏土三轴蠕变试验和剪切破坏试样如图2，3所示。

2试验结果及分析

2.1固结不排水剪切试验结果

根据三轴固结不排水试验得到偏应力-应变关系如图4所示。在轴向应变ε=0%～5%时，偏应力值增幅明显；在轴向应变ε≥5%时，偏应力增长趋势平缓，但没有出现应力峰值现象。根据《土工试验规程》，当三轴固结不排水剪切试验无应力峰值时，取轴向应变ε=15%所对应的偏应力值作为剪切破坏偏应力，即qf=161.41 kPa。

2.2蠕变试验结果

2.2.1蠕变试验曲线

由第2.1节确定的剪切破坏偏应力qf=161.41 kPa可知，蠕变试验每级轴向加载偏应力Δqf=40.35 kPa。蠕变试验应变时程曲线如图5所示，其中Qf为轴向偏应力。

由图5可知：成都黏土在低应力条件下有瞬时弹性变形，并且弹性变形在一定时间内随着应力的增加而增加，随后变形趋于稳定；在较高应力条件下，成都黏土仍会有瞬时弹性变形，但在随后的时间里，黏土的变形会先暂时趋于稳定，在一定时间过后，变形有小幅增加，随后趋于稳定。这说明在较高应力条件下土体在宏观上虽然可以保持一定时间的稳定，但实际上在土体内部的一些软弱结构面和裂缝处均在发生着随时间流动的不利变形，并且这些不利变形会逐渐积累；最后，高应力会触发积累的不利变形，导致在该阶段试样发生加速蠕变，直至破坏。

2.2.2成都黏土长期强度

根据蠕变试验可以得出成都黏土的应力-应变曲线，如图6所示，其中t为时间。

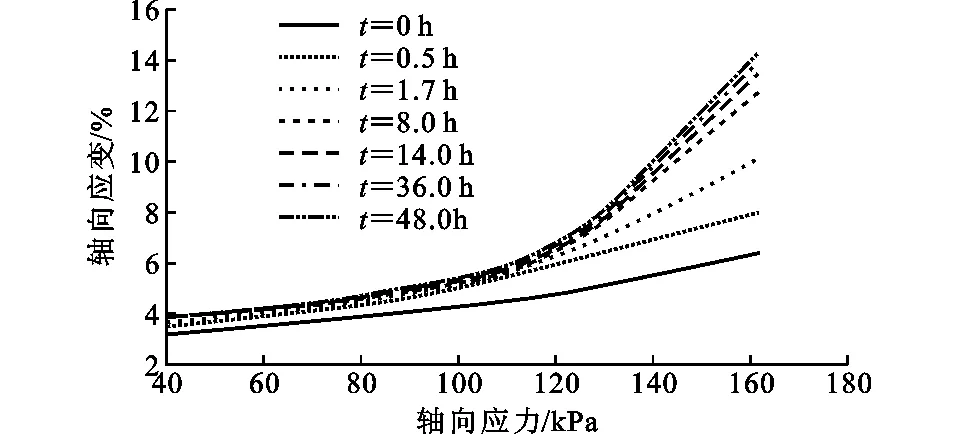
由图6可知：在时间相等的情况下，随着轴向应力的增加，应变整体上也相应的增加，在轴向应力σ=121.05 kPa时，曲线产生拐点，该拐点的应力即为成都黏土在围压为100 kPa条件下的长期强度τ∞，τ∞=121.05 kPa；在t=0 h时的应力-应变曲线与其他时间的曲线是分开的，说明在t=0～0.5 h时所有等级的应力条件都发生了应变突变，这可能是黏土瞬时弹性变形引起的。

2.2.3成都黏土弹性模量

根据蠕变试验，成都黏土的弹性模量E与时间t和轴向应力σ的关系如图7所示。

由图7可知：成都黏土的弹性模量E在恒定荷载作用下会随着t的增加而减小；在施加轴向应力σ结束后，E会迅速减小到一定值，随后缓慢减小，趋于稳定，这表明E具有时效特性；在土体结构破坏前，E会随着σ的增加而增加，增速随σ的增加而减小，当作用极限破坏荷载时，E会出现跌落式骤减现象，这表明E具有加载特性。上述现象的出现可解释为：土体在正常固结后，在低应力条件下，黏土受到压缩，孔隙、裂隙减小，使土体达到超固结状态，一定程度上增加了土体的有效应力，因此E会随σ的增加而增加；在高应力作用下，一些已经存在的或正在发生的裂缝和结构面在短时间内加速形成或扩大，并形成一定规模，最终引起土体整体破坏，从而使得E瞬间骤减。

2.2.4成都黏土黏滞系数

成都黏土黏滞系数η与时间t和轴向应力σ的关系如图8所示。当σ小于黏土屈服强度并且σ恒定时，η随t的增加而增加，随后稳定，这表明η具有时效特性；当σ小于屈服强度并且时间恒定时，η随σ的增加而增加，当σ大于屈服强度时，η随t的增加出现跌落式减小现象，表明黏滞系数具有加载特性。

3分数阶导数非定常蠕变模型推导

3.1分数阶导数软体元件

分数阶微积分是研究任意阶次的微分、积分算子特性的一种数学方法。在黏土元件流变模型中采用分数阶导数可以克服整数阶流变模型与试验数据吻合差的缺点，具有以下优点：比一般非线性蠕变模型的参数更少，方程更简洁，物理意义更明显，适用范围更广。因此，本文在推导成都黏土蠕变模型时引入分数阶导数。

在描述岩土体的流变特性时，采用Riemann-Liouville[14-15]理论(R-L理论)定义。根据R-L理论，假设函数f在(0，+∞)上连续可积，对于t>0，分数阶阶次n≥0，有

(1)

式中：Γ(n)为Gamma函数；ξ为积分变量。

在材料力学中，对于理想固体材料，应力-应变关系满足

σ(t)=Eε(t)

(2)

对于理想流体材料，应力-应变关系满足

(3)

在实际工程中，黏土大多表现出的材料属性既不是理想固体材料，也不是理想流体材料，而是介于两者之间。根据文献[16]建立的用来描述介于理想固体和理想流体之间材料状态的软体元件关系，有

(4)

式中：当0≤n≤1时，建立的为分数阶导数本构方程，当n=0时，材料表现为理想固体属性，当n=1时，材料表现为理想流体属性。

当应力σ(t)=const时，黏土的蠕变特性可以用上面的软体元件来描述，基于Riemann-Liouville分数阶理论，对式(4)分数阶积分得

(5)

式(5)为分数阶黏滞体的蠕变本构方程，此时0≤n≤1。对式(5)取σ(t)=80.50 kPa，η=20 kPa·h，可得到n取不同值时蠕变曲线的变化趋势，如图9所示。当n在[0,1]区间范围内，随着n值的增大，软体元件描述的蠕变曲线所表现出的线性特性越来越显著，当n=1时，软体元件表现出完全线性特性，即此时的软体元件为牛顿黏壶。

3.2分数阶导数蠕变模型的建立

根据夏才初等[17]提出的蠕变模型辨识方法和本文蠕变试验结果，成都黏土的蠕变变形在低应力水平条件下仅有衰减蠕变，此时黏土的变形仅具有弹性变形；在高应力水平条件下，黏土变形表现出加速蠕变，此时黏土同时表现出黏弹性变形和黏塑性变形。因此，成都黏土的蠕变具有瞬时弹性变形、黏弹性变形和黏塑性变形，具体模型如图10所示，其中，E1为弹性元件的弹性模量，即初始弹性模量，E2为黏弹性元件的弹性模量，η1为软体元件黏滞系数，η2为黏塑性元件初始黏滞系数，σL为黏土屈服强度。

黏土在蠕变过中，当蠕变荷载一定时，随着时间的变化，黏土内部结构发生变化，孔隙水压力和有效应力重新分布，应变随时间变化与应力表现出非线性特性，这种非线性特性用分数阶导数描述；同时，为了更加准确地描述这种非线性特性，在蠕变模型中考虑弹性模量和和黏滞系数的非定常性，即时效特性和加载特性。

成都黏土非定常蠕变本构模型假定在t=0 h时，在模型上施加轴向应力σ，那么蠕变总变形为

ε′=εe+εve+εvp

(6)

式中：ε′为总应变；εe为弹性应变；εve为黏弹性应变；εvp为黏塑性应变。

3.2.1瞬时弹性元件应变

瞬时弹性应变由以下公式求解

(7)

3.2.2黏弹性元件应变

软体黏弹性元件其实就是在Kelvin体的基础上将其黏性元件用软体元件替换，并使用分数阶导数推导模型，具体模型关系如下

(8)

式中：ε1，ε2分别表示为黏弹性元件的弹性应变和软体元件应变。

对式(8)做变换得

(9)

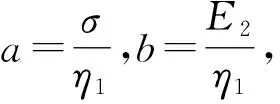
(10)

对式(10)做拉普拉斯逆变换得

(11)

式中：i为求和次数。

将a，b代入式(11)得

(12)

3.2.3黏塑性元件应变

根据黏塑性元件中塑性元件的特点，得到其应力σvp为

(13)

当σ<σL时，黏塑性元件不在蠕变模型中引起应变，此时蠕变模型描述的是衰减蠕变阶段；当σ≥σL时，黏塑性元件在蠕变模型中引起应变，其应变有以下关系

(14)

式中：εvp为黏塑性元件应变；σvp为黏塑性元件应力。

结合式(13)，对式(14)进行蠕变本构求解得

(15)

综上推导，成都黏土非线性蠕变方程有：

当σ<σL时

(16)

当σ≥σL时

(17)

3.3蠕变方程参数非定常性

黏土由于荷载的作用，土体内部的孔隙和裂隙等被挤压紧密，致使黏土的应力分布重新调整，在局部应力集中区，孔隙或裂隙开始发育、生长，甚至贯通。这些不利土体结构的出现和发展，会导致黏土材料的损伤，加剧材料的破坏过程。

3.3.1成都黏土弹性模量

根据蠕变试验分析，弹性模量具有时效特性和加载特性，表明弹性模量与加载应力和时间存在函数关系。在一维应力状态下，蠕变损伤服从下式[18]

(18)

对式(18)进行积分得

D(t)=1-[1-tm(k+1)σk]1/(k+1)

(19)

根据损伤力学原理，任意时刻的弹性模量为

E(t)=Ei[1-D(t)]

(20)

式中：Ei为黏土各蠕变阶段的初始弹性模量。

将式(19)代入式(20)得

E(t)=Ei[1-tm(k+1)σk]1/(k+1)

(21)

3.3.2成都黏土黏滞系数

根据蠕变试验的黏滞系数分析结果可知，黏滞系数与加载应力、时间存在函数关系。孙钧[18]认为，在加载应力大于长期强度时，黏滞系数不断减小，影响因素主要有黏土长期强度、时间和加载水平。因此，引入指数函数η(t)

η(t)=η2e-(σ-τ∞)pt

(22)

式中：p为材料参数。

综上所述，将式(21)，(22)代入式(16)，(17)，构成成都黏土非定常蠕变本构模型。

当σ<σL时

(23)

当σ≥σL时

(24)

3.4蠕变本构模型辨识分析

本文通过1stOpt软件中的LM(Levenberg-Marquardt)算法，对建立的蠕变模型进行参数拟合分析。该算法具有不易于收敛到局部极小值和对初值依赖性不强等优点[19]，可以满足参数拟合要求。成都黏土蠕变模型的拟合结果见图11和表2。

根据拟合结果可知：成都黏土非线性蠕变模型的弹性模量和黏滞系数在低、中应力条件下均随轴向偏应力的增大而增大；在高应力条件下，二者均出现跌落式减小，这符合蠕变试验的研究规律。在速蠕变阶段，蠕变试验的数据与公式的拟合度可达0.999，这克服了许多蠕变模型不能较好反映加速蠕变阶段的难题。

为说明所构建模型的合理性和可靠性，用本文构建的蠕变模型对文献[20]中的成都黏土蠕变试验数据进行拟合辨识，辨识结果见图12和表2。根据辨识结果可知，文献[20]中的蠕变试验数据与拟合曲线辨识度较高，表明本文蠕变模型能较准确地反映成都黏土的蠕变过程。

因此，本文所建立的蠕变模型是可行的，能从一定程度上反映成都黏土蠕变的本质，这对成都黏土蠕变性质的研究具有借鉴意义。

表2蠕变模型拟合参数Tab.2Fitting Parameters of Creep Model

4结语

(1)通过成都黏土的常规固结不排水试验和蠕变试验及分析，确定了试验黏土的峰值偏应力；成都黏土的蠕变过程主要包括瞬时弹性变形、黏弹性变形和黏塑性变形；黏土的弹性模量和黏滞系数在黏土未达屈服强度时均随轴向应力的增加而增加，黏滞系数随时间的增加而增加，弹性模量则反之；在达到屈服强度后，二者均随时间的增加而发生跌落式减小；弹性模量和黏滞系数均有时效特性和加载特性，即二者具有非定常性。

(2)基于分数阶导数理论，结合蠕变试验发现弹性模量和黏滞系数的非定常性，在蠕变模型中引入关于弹性模量和黏滞系数的函数式，从而建立了成都黏土的非定常蠕变本构模型。

(3)对所建立的蠕变模型进行拟合分析，结果表明本文构建的模型能够较好反映成都黏土弹性模量和黏滞系数的变化规律；同时在加速蠕变阶段的拟合度极高，说明该蠕变模型能较好地反映成都黏土的蠕变特性；通过辨识分析，本文蠕变模型能够很好地拟合相关学者关于成都黏土的蠕变试验数据，表明了本文所建蠕变模型的合理性和可靠性。

(4)本文以成都黏土为背景，建立的蠕变模型能够较好反映蠕变特性，但也存在蠕变模型较为复杂的问题，这是由于在分数阶导数的基础上引入弹性模量和黏滞系数函数式。因此，如何使得蠕变模型既能更好地反映成都黏土蠕变特性，又能更加简洁将是需要研究的方向之一。

参考文献：

References:

[1] 周秋娟,陈晓平.软土蠕变特性试验研究[J].岩土工程学报,2006,28(5):626-630.

ZHOU Qiu-juan,CHEN Xiao-ping.Experimental Study on Creep Characteristics of Soft Soils[J].Chinese Journal of Geotechnical Engineering,2006,28(5):626-630.

[2] 李珍玉,肖宏彬,金文婷,等.南宁膨胀土非线性流变模型研究[J].岩土力学,2012,33(8):2297-2302.

LI Zhen-yu,XIAO Hong-bin,JIN Wen-ting,et al.Study of Nonlinear Rheological Model of Nanning Expansive Soils[J].Rock and Soil Mechanics,2012,33(8):2297-2302.

[3] 肖宏彬,贺 聪,周 伟,等.南宁膨胀土非线性剪切应力松弛特性试验[J].岩土力学,2013,34(增1):22-27.

XIAO Hong-bin,HE Cong,ZHOU Wei,et al.Experimental Study of Nonlinear Shear Stress Relaxation Characteristics of Nanning Expansive Soil[J].Rock and Soil Mechanics,2013,34(S1):22-27.

[4] 肖宏彬,范志强,张春顺,等.非饱和膨胀土非线性流变特性试验研究[J].公路工程,2009,34(2):1-5,26.

XIAO Hong-bin,FAN Zhi-qiang,ZHANG Chun-shun,et al.Experimental Study on Non-linear Rheological Characteristics of Unsaturated Expansive Soils[J].Highway Engineering,2009,34(2):1-5,26.

[5] 肖宏彬,马千里,金文婷.非饱和膨胀土非线性经验蠕变模型的研究[J].中南林业科技大学学报,2011,31(6):1-5.

XIAO Hong-bin,MA Qian-li,JIN Wen-ting.Experimental Study on Experiential Model Considering Non-linear Creep of Unsaturated Expansive Soil[J].Journal of Central South University of Forestry & Technology,2011,31(6):1-5.

[6] 肖宏彬,范志强,苗 鹏.基于膨胀土蠕变试验的粘弹性模型对比研究[J].自然灾害学报,2009,18(3):72-78.

XIAO Hong-bin,FAN Zhi-qiang,MIAO Peng.Comparative Study on Viscoelastic Models Based on Creep Tests of Expansive Soils[J].Journal of Natural Disasters,2009,18(3):72-78.

[7] 殷德顺,任俊娟,和成亮,等.一种新的岩土流变模型元件[J].岩石力学与工程学报,2007,26(9):1899-1903.

YIN De-shun,REN Jun-juan,HE Cheng-liang,et al.A New Rheological Model Element for Geomaterials[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(9):1899-1903.

[8] 殷德顺,和成亮,陈 文.岩土应变硬化指数理论及其分数阶微积分理论基础[J].岩土工程学报,2010,32(5):762-766.

YIN De-shun,HE Cheng-liang,CHEN Wen.Theory of Geotechnical Strain Hardening Index and Its Rationale from Fractional Order Calculus[J].Chinese Journal of Geotechnical Engineering,2010,32(5):762-766.

[9] 殷德顺,任俊娟,和成亮,等.基于分数阶微积分理论的软土应力-应变关系[J].岩石力学与工程学报,2009,28(增1):2973-2979.

YIN De-shun,REN Jun-juan,HE Cheng-liang,et al.Stress-stain Relation of Soft Soil Based on Fractional Calculus Operators Theory[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(S1):2973-2979.

[10] 何志磊,朱珍德,朱明礼,等.基于分数阶导数的非定常蠕变本构模型研究[J].岩土力学,2016,37(3):737-744,775.

HE Zhi-lei,ZHU Zhen-de,ZHU Ming-li,et al.An Unsteady Creep Constitutive Model Based on Fractional Order Derivatives[J].Rock and Soil Mechanics,2016,37(3):737-744,775.

[11] 郭佳奇,乔春生,徐 冲,等.基于分数阶微积分的Kelvin-Voigt流变模型[J].中国铁道科学,2009,30(4):1-6.

GUO Jia-qi,QIAO Chun-sheng,XU Chong,et al.The Kelvin-Voigt Rheological Model Based on Fractional Calculus[J].China Railway Science,2009,30(4):1-6.

[12] 陈 亮,陈寿根,张 恒,等.基于分数阶微积分的非线性黏弹塑性蠕变模型[J].四川大学学报:工程科学版,2013,45(3):7-11.

CHEN Liang,CHEN Shou-gen,ZHANG Heng,et al.A Nonlinear Viscoelasto-plastic Creep Model Based on Fractional Calculus[J].Journal of Sichuan University:Engineering Science Edition,2013,45(3):7-11.

[13] 李锐铎,乐金朝.基于分数阶导数的软土非线性流变本构模型[J].应用基础与工程科学学报,2014,22(5):856-864.

LI Rui-duo,YUE Jin-chao.Nonlinear Rheological Constitute of Soft Soil Based on Fractional Order Derivative Theory[J].Journal of Basic Science and Engineering,2014,22(5):856-864.

[14] KOELLER R C.Application of Fractional Calculus to the Theory of Viscoelasticity[J].Journal of Applied Mechanics,1984,51(2):299-307.

[15] ADOLFSSON K,ENELUND M,OLSSON P.On the Fractional Order Model of Viscoelasticity[J].Mechanics of Time-dependent Materials,2005,9(1):15-34.

[16] SCOTT-BLAIR G W.Analytical and Integrative Aspects of the Stress-strain-time Problem[J].Journal of Scientific Instruments,1944,21(5):80-84.

[17] 夏才初,王晓东,许崇帮,等.用统一流变力学模型理论辨识流变模型的方法和实例[J].岩石力学与工程学报,2008,27(8):1594-1600.

XIA Cai-chu,WANG Xiao-dong,XU Chong-bang,et al.Method to Identify Rheological Models by Unified Rheological Model Theory and Case Study[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1594-1600.

[18] 孙 钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.

SUN Jun.Rheology of Geo-material and Its Engineering Application[M].Beijing:China Architecture & Building Press,1999.

[19] 朱杰兵,汪 斌,邬爱清.锦屏水电站绿砂岩三轴卸荷流变试验及非线性损伤蠕变本构模型研究[J].岩石力学与工程学报,2010,29(3):528-534.

ZHU Jie-bing,WANG Bin,WU Ai-qing.Study of Unloading Triaxial Rheological Tests and Its Nonlinear Damage Constitutive Model of Jinping Hydropower Station Green Sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):528-534.

[20] 张晓超,郑海军.成都黏土蠕变试验及其蠕变模型研究[J].实验技术与管理,2010,27(10):52-55.

ZHANG Xiao-chao,ZHENG Hai-jun.Creep Tests on Chengdu Clay and Its Creep Models[J].Experimental Technology and Management,2010,27(10):52-55.