井场作业人员应急疏散仿真研究*

同 霄，周立辉，冀忠伦

(1.长庆油田分公司 油气工艺研究院，陕西 西安 710018；2.低渗透油气田勘探开发国家工程实验室，陕西 西安 710018)

0 引言

井控安全是油气田开发安全管理的重点，一旦发生井喷失控事故，其造成的人员、环境、设备、油气藏伤害及社会影响后果是相当严重的。在油气田钻井作业和压裂、试油、修井等井下作业过程中，尤其是高压油气井(预测井口关井压力可能超过35 MPa)、高含硫油气井(地层天然气中硫化氢含量大于150 mg/m3)以及高危地区油气井(井口周围500 m范围内有村庄、学校、医院等人员密集场所或是易燃易爆物品存放点和水资源设施)，发生溢流、气侵以及井喷的风险较大，若发生井喷失控，将会造成重大损失。2003年12月23日晚21时15分，中石油西南油气田分公司川东北气矿罗家16H井，在起钻作业中，突然发生溢流，造成井喷失控，共造成243人死亡，6万余名群众紧急疏散，直接经济损失近亿元[1]。2003年9月15日晚8时30分，湖北省利川市建南镇黄金村一口废弃的井口突然发生强烈的天然气井喷，经过消防官兵10天的英勇奋战，最终控制住灾情，所幸没有造成人员伤亡[2]。针对油气井周边居民的安全疏散问题，姜传胜等[3]研究评估了居民的疏散安全现状，并提出了疏散方案。针对油气井现场作业人员的安全疏散问题，目前研究较少。井喷失控后，现场应立即启动应急预案，进行人员疏散，当现场发生爆炸和火灾等严重事故时，所有现场作业人员需迅速撤离至安全区域。为了确保现场作业人员的人身安全，必须建立一套完整的方法来评估作业人员的疏散安全水平，规划和制定详细的应急指挥方案，所以研究井场作业人员的疏散过程具有一定的指导意义。

目前，对于人员疏散过程的研究主要分为宏观和微观2种方法。宏观方法认为人群为连续的流动介质，通过流体力学模型计算人群的移动状态，该方法的缺点是不能充分考虑人群的个体特征。微观方法中包括连续模型和离散模型2类，1995年，Helbing等[4-5]首次提出的社会力模型是最典型的连续模型。近年来，国内外学者针对传统的社会力模型展开了各种的改进研究，从而更加准确地模拟行人的紧急疏散。传统社会力模型对于单个行人的运移或者数量较少人群的疏散计算结果失真，针对这一缺陷Lakoba等[6]进行了改进；Parisi等[7]通过分析疏散试验的结果，对社会力模型进行修正，引入行人的自动停止机制，仿真计算结果更加接近真实情况；隋杰等[8]和龙圣杰等[9]将社会力模型与高斯烟团扩散模型结合，对地铁毒气扩散事件中行人的疏散过程进行了研究；牟瑞芳等[10]拓展了社会力模型，模拟了行人在熟悉情况下的疏散行为；Han和Liu[11]基于学校学生的疏散演习，引入回避策略和行人间的信息交流模型，从而更加准确的模拟了行人的疏散过程，通过分析真实疏散试验数据来改进计算模型，是1种行之有效的研究方法。离散模型中应用较为广泛的为元胞自动机模型，该方法由Neumann[12]在1966年最先提出，后续众多学者对该模型进行了改进和拓展[13-17]。元胞自动机模型虽然规则简单，运算速度快，但是由于该模型划分的网格是规则形状，行人移动的方向受到约束，是不能在空间中自由移动的，难以真实表达人群的移动疏散过程。因此，针对井场作业人员的应急疏散问题，本文以压裂作业为例，选用社会力模型进行仿真计算，计算结果对评估作业人员的疏散水平、分析作业井场的安全薄弱环节以及制定应急指挥方案具有一定的指导意义。

1 社会力模型

Helbing等[4-5]提出的社会力模型是最典型的连续模型之一。该模型将行人视为满足力学定律的质点，如式(1)所示：

(1)

随着行人所受外力的改变，行人的运动也随之变化，行人受4种作用力的共同约束，如式(2)所示：

(2)

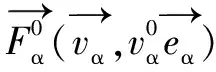
在社会力模型中驱动力是决定行人以期望速度向目的地运动的力，如式(3)所示：

(3)

行人运动过程中通常会遇到来自其他行人的干扰，为避免与其他行人发生碰撞，在社会力模型中用力的形式来表现这种行人之间的避让行为。行人之间作用力分为2种：社会心理力和社会物理力，前者描述了由避让心理导致的避让行为，如式(4)所示；后者为接触力，当行人相互接触时产生，如式(5)所示。

(4)

(5)

行人与边界或障碍物之间的作用力和行人之间的作用力类似，包括描述行人躲避障碍物的避让作用力和与障碍物接触时的挤压作用力，如式(6)所示：

(6)

式中：角标B代表障碍物，其余参量的含义与单位与式(3)-(5)一致，描述了行人与障碍物之间的关系。

2 计算模型

压裂是被广泛采用的油气井增产和水井增注的主要措施之一，是油气田勘探和开发中不可缺少的重要技术手段。压裂作业过程中所涉及的动力机械设备很多，这些设备能造成高压条件，泵送高压液体，快速均匀搅拌混砂液体。通常压裂车组由压裂车、混砂车、仪表车、起重机、射孔车、储液罐、砂罐车等组成，本文中计算模型选用陇东PG49-51压裂井场，根据现场测量，混砂车整车外形尺寸13.0 m×2.5 m、压裂车整车外形尺寸11.0 m×2.5 m、射孔车整车外形尺寸8.5 m×2.5 m、仪表车整车外形尺寸9.5 m×2.5 m、储液罐外形尺寸10.0 m×3.0 m、起重机整车外形尺寸15.0 m×3.0 m、彩钢房外形尺寸5.5 m×3.5 m、砂罐车整车外形尺寸8.0 m×2.5 m，如图1(a)所示。该井完钻井身3 676.0 m，水平段长1 699.6 m，采用大通径桥塞体积压裂工艺，井控提示应做好一氧化碳和硫化氢等有害气体的防范措施，防止有毒有害气体溢出，为一级井控风险井[18]。井场尺寸为60 m×65 m，位于沟壑纵横的黄土塬，井场周围被深沟和台阶切割，连通井场与外界的道路宽4 m，如图1(b)所示，根据井场设备布局和作业人员工作范围将井场分为工具存放区域、高压区域、低压区域、储液配液区域、射孔装弹区域、混砂区域、生活区域和位于出口处的应急集中区域。

图1 压裂井场布置和作业人员分布示意Fig.1 Schematic diagram of fractured well field and distribution of workers

根据现场调查，压裂井场作业人员一般包括5个部分：试油作业人员、压裂作业人员、射孔作业人员、司机和其他人员，如图1(c)所示。其中，试油作业人员的工作区域集中在储液配液区和混砂区，在压裂过程中负责按施工设计配置压裂液和携砂液，试油队的人员通常分为两班，其余人员在生活区域休息；压裂作业人员主要包括操作每台压裂车的人员和压裂仪表车上的2-3名压裂技术人员，通常压裂开始后压裂车的操作人员会离开高压区域，在低压区域等待压裂结束，仪表车上还有1名技术支撑人员和1名工程监督；射孔作业人员的工作区域集中在射孔装弹区域，在压裂开始后，射孔队的作业人员一般是在进行下一次的压裂的提前准备工作；砂罐车司机停车后，通常进入生活区域休息待命；其他人员中包括厨师和配送人员等，活动范围集中在生活区域。

在仿真计算中，为了便于模拟人员的疏散过程，将仪表车和彩钢房内工作和休息的作业人员位置调整在外部空间，简化了人员下车和离开房间的过程，将储液罐顶部的工作人员位置调整在储液罐附近，简化了人员从储液罐顶部移动到地面的过程。同时针对社会力模型在反映疏散者个体特征差异方面并无多大优势的缺陷，以作业人员的工作区域为小组，将压裂井场的作业人员分为5组：第1组(仪表车附近)共4名，包括压裂技术人员2名、监督1名和技术支撑人员1名；第2组(混砂车附近)共4名，包括混砂工人2名和砂罐车司机2名；第3组(射孔装弹区域)为射孔队的5名工作人员；第4组(储液罐附近)共12名，包括压裂车司机6名和试油队配液人员6名；第5组(生活区域)共10名，包括试油队休息人员6名、砂罐车司机3名和厨师1名，这样在计算中可以对这5组作业人员的分别选择计算参数，通过该方法考虑疏散者个体特征差异。

整个压裂井场共有35名作业人员，采用社会力模型，通过编写程序，模拟压裂井场作业人员的应急疏散过程，初始时刻人员分布于各自的工作区域，当发生井喷、一氧化碳和硫化氢泄漏等突发事件，且防喷井口抢装失败后，导致井喷失控，并伴随燃爆。此时井场内所有作业人员迅速撤离至指定的应急集中区域。

疏散速度是人员疏散仿真计算的基础，李利敏和闫金鹏[19]通过实验测定得到正常状态下成年人在明亮和昏暗2种外界条件下的移动速度分别为1.26～1.48 m/s和1.22～1.42 m/s，紧急状态时成年人在明亮和昏暗2种外界条件下的移动速度分别为1.55～2.07 m/s和1.52～2.07 m/s；井场作业人员为成年人，穿戴专业作业服装和鞋帽，有一定的负重，Chen等[20]对不同负重行人移动速度测试的结果表明，当负重从0 kg增加至10 kg，移动速度平均降低27.05%；作业人员熟悉井场布置和线路，根据牟瑞芳等[10]对熟悉环境条件情况下人员疏散进行仿真计算，模拟结果中行人的平均移动速度为1.8 m/s；井喷失控后伴随着火灾爆炸，烟气会导致能见度降低，根据Seike等[21](2017)对不同能见度下行人的应急疏散速度实验研究发现，随着消光系数的从0.30 m-1增高至0.98 m-1(能见度降低)，人员的移动速度从最初的1.83 m/s下降至1.46 m/s。综合上述学者的研究成果，结合对现场作业人员的移动速度观测，本文选取的行人最大期望速度为2.0 m/s，最小期望速度为1.5 m/s，其余计算参数选择如表1所示[22-24]。

表1 社会力模型计算参数Table 1 Calculation parameters of the social force model

3 计算结果

在计算过程每秒输出1次计算结果，这样可以更好地分析井场作业人员的疏散过程，如图2所示。t=0 s时刻为初始状态，5组作业人员分别处于各自的工作区域(图2(a))；随着突发事件的发生，人员开始紧急向应急集中区域撤离，当t=5 s时刻(图2(b))，砂罐车附近的4名作业人员因为离出口处最近，沿路无障碍，所以首先转移至应急集中区域，其他各组人员也离开自己的工作区域，向着应急集中区域移动，其中射孔队的作业人员在移动中受到了井场内停放的砂罐车一定程度的阻挡；当t=10 s时刻(图2(c))，各组作业人员保持正常疏散，射孔队和仪表车共9名作业人员也绕过砂罐车向着应急集中区域继续移动；当t=17 s时刻(图2(d))，射孔队和部分生活区的作业人员安全抵达应急集中区域，其他各组保持正常疏散，唯有液罐的12名作业人员在疏散路径中遇到了阻碍，由于混砂车旁卸砂的砂罐车与储液罐之间的空间较小，所以在此处出现拥堵现象，并呈现出拱形分布；当t=25 s时刻(图2(e))，各组人员正常疏散，液罐的作业人员也排队离开狭窄区域，向着应急集中区域移动；当t=40 s时刻(图2(f))，人员已基本安全疏散至应急集中区域。

根据计算结果，统计得到疏散人数随时间的变化曲线，如图3所示。可以看出，仪表车4人安全疏散用时共25 s(图3(a))，射孔队5人安全疏散用时共20 s(图3(b))，砂罐车4人安全疏散用时最短，共10 s(图3(c))，液罐12人安全疏散用时最长，共47 s(图3(d))，生活区10人安全疏散用时共28 s(图3(e))，整个井场35名作业人员安全疏散共用时为47 s(图3(f))。2009年10月，中国石油在四川油气田虚拟发生井喷失控着火事故，进行了一次全过程、全方位的井喷突发事件应急预案专项演练。分析演练数据，自发生溢流当班人员发出警报，至井队的作业人员迅速跑向紧急集中区域完成集中，共用时178 s。与应急演练用时相比，仿真计算用时较短，这是由于在仿真计算中简化了作业人员下车、下罐和离开房间的过程，同时没有考虑路面条件(如摆放管线、路面不平)对疏散人员的阻碍效应。仿真计算结果虽然与应急演练结果有一定的差距，但是可以间接反映不同区域作业人员的疏散水平，可用于评估应急疏散效果、指导应急疏散。

图2 压裂井场作业人员疏散过程Fig.2 The evacuation process of the workers in the fractured well field

图3 疏散人数随时间的变化曲线Fig.3 The curve of the number of evacuation people with time

为了更好的指导实际应急疏散，本文进一步分析仿真计算结果，将每位疏散人员的运动轨迹进行跟踪统计，绘制得到压裂井场作业人员的疏散路径，如图4所示。仪表车和射孔队的作业人员在疏散过程中，受到了a处砂罐车的阻碍，降低了疏散效率。同时井场布置时在c处设置了卫生间，使得该处道路封堵，导致仪表车和射孔队的作业人员只能绕行至砂罐车的另一侧移动至应急集中区域，增加了安全疏散时间。生活区和砂罐车的作业人员距离应急集中区域较近，且疏散路径宽敞无障碍，所以疏散过程平稳，效率较高。突发事件发生时，高压区域布满了高压管汇，不能作为疏散路径，液罐的作业人员只能通过液罐附近的低压区域移动至生活区，再移动至安全区域。井场布置时液罐前期已经摆放固定，b处的砂罐车停放位置有误，使得液罐和砂罐车距离狭窄，导致了液罐人员在疏散至此处时发生拥堵现象，降低了疏散效率，增大了危险性。由于液罐人员离应急集中区域最远，疏散路径较长，在地形条件的允许下，可考虑增大d处蓄水池和压裂车之间的空间，同时设置e区域为另一处的应急集中区域，这样可使液罐人员安全迅速的抵达应急集中区域，提高整体的疏散效率。通过对疏散路径的分析，可以明确作业人员的常规疏散路径，在实际的工作中，要保证疏散路径的路面平整，畅通无阻。同时计算结果可以指导井场布置，制定更为合理的应急方案，提高作业人员安全保障。社会力模型也可运用至石油钻井作业和采油作业中，分析指导实际的应急指挥和方案制定。

图4 压裂井场作业人员疏散路径Fig.4 Evacuation path of workers in fractured well filed

4 结论

1)利用社会力模型计算压裂井场作业人员的疏散过程，其结果可以间接反映不同区域作业人员的疏散水平，可用于评估应急疏散效果。

2)基于仿真计算结果分析，可为井场设施摆放、临时房屋建设，应急集中区域选择等科学布置井场提供参考依据，同时可指导应急疏散方案的制订。

3)为了更加真实地模拟和分析发生井喷失控等事故时现场作业人员的疏散过程，在本文工作的基础上，可进一步改进社会力模型，例如考虑更加全面的行人个体特性、面临突发事件时心理素质水平和道德水平，同时，开展实际场地的疏散实验，利用实验结果优化分析模型。

[1] 滕五晓. 公共安全管理中地方政府的责任及其作用——以重庆市开县井喷事故灾害为例[J]. 社会科学, 2005(12):65-71.

TENG Wuxiao. Responsibilities and functions of local governments in public safety management—Taking Kaixian's blowout accident in Chongqing as an example[J]. Social Science, 2005(12):65-17.

[2] 李金文, 陈先斌. “9·15”利川天然气井喷事故处置对策[J]. 消防科学与技术, 2004, 23(2):188-191.

LI Jinwen, CHEN Xianbin. Countermeasures to the blowout of "9·15" Lichuan natural gas mine[J]. Fire Science and Technology, 2004, 23(2):188-191.

[3] 姜传胜, 邓云峰, 席学军. 高含硫气井周边居民疏散安全分析方法[J]. 中国安全科学学报, 2007, 17(9):9-13.

JIANG Chuansheng, DENG Yunfeng, XI Xuejun. Safety analysis on the evacuation of residents around natural gas wells with high hydrogen sulfide content[J]. China Safety Science Journal, 2007, 17(9):9-13.

[4] HELBING D, MOLNR P. Social force model for pedestrian dynamics[J]. Physical Review. E, Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 1995, 51(5): 4282-4286.

[5] HELBING D, FARKAS I, VICSEK T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407(683): 487-490.

[6] LAKOBA T I, KAUP D J, FINKELSTEIN N M. Modifications of the Helbing-Molnar-Farkas-Vicsek social force model for pedestrian evolution[J]. Simulation-Transactions of the Society for Modeling and Simulation International, 2005, 81(5): 339-352.

[7] PARISI D R, GILMAN M, MOLDOVAN H. A modification of the Social Force Model can reproduce experimental data of pedestrian flows in normal conditions[J]. Physica a: Statistical Mechanics and Its Applications, 2009, 388(17): 3600-3608.

[8] 隋杰, 万佳慧, 于华. 基于社会力的应急疏散仿真模型应用研究[J]. 系统仿真学报, 2014, 26(6):1197-1201.

SUI Jie, WAN Jiahui, YU Hua. Research on simulation of emergency evacuation based on social force model[J]. Journal of System Simulation, 2014, 26(6):1197-1201.

[9] 龙圣杰, 刘衍民, 隋杰. 生化恐怖袭击情境下引导疏散中行人行为仿真研究[J]. 中国安全生产科学技术, 2016, 12(7):174-179.

LONG Shengjie, LIU Yanmin, SUI Jie. Study on simulation of pedestrian behaviors in guided evacuation under biochemical terrorist attack[J]. Journal of Safety Science and Technology, 2016, 12(7):174-179.

[10] 牟瑞芳, 杨锐, 王列妮. 熟悉环境条件下的公共场所人员疏散仿真模型研究[J]. 中国安全生产科学技术, 2015,11(5):181-186.

MU Ruifang, YANG Rui, WANG Lieni. Study on simulation model of public place evacuation in a familiar environment[J]. Journal of Safety Science and Technology, 2015,11(5):181-186.

[11] HAN Yanbin, LIU Hong. Modified social force model based on information transmission toward crowd evacuation simulation[J]. Physica a: Statistical Mechanics and Its Applications, 2017, 469: 499-509.

[12] SCHWARTZ J T, BURKS A W. Theory of Self-Reproducing Automata[J]. Quarterly Review of Biology, 1966, 21(100):745.

[13] NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal de Physique I, 1992, 2(12): 2221-2229.

[14] WOLF D E. Cellular automata for traffic simulations[J]. Physica A-statistical Mechanics & Its Applications, 1999, 263(1-4):438-451.

[15] 杨立中, 方伟峰, 黄锐,等. 基于元胞自动机的火灾中人员逃生的模型[J]. 科学通报, 2002, 47(12):896-901.

YANG Lizhong, FANG Weifeng, HUANG Rui, et al. Model of personnel escape in fire based on Cellular Automata[J]. Chinese Science Bulletin, 2002, 47(12):896-901.

[16] 张立红, 陈海涛, 杨鹏,等. 心理迫切因素对行人疏散动力学的影响研究[J]. 中国安全生产科学技术, 2013, 9(6):79-84.

ZHANG Lihong, CHEN Haitao, YANG Peng,et al. Study on influence of psychological urgency parameter on pedestrian evacuation dynamics[J]. Journal of Safety Science and Technology, 2013, 9(6):79-84.

[17] 陈海涛, 刘占, 张立红,等. 低可见度情况下从众行为对疏散的影响分析[J]. 中国安全生产科学技术, 2016, 12(8):165-170.

CHEN Haitao, LIU Zhan, ZHANG Lihong, et al. Influence of herd behavior on evacuation under limited visibility[J]. Journal of Safety Science and Technology, 2016, 12(8):165-170.

[18] 石油天然气井下作业井控编写组. 石油天然气井下作业井控[M]. 北京：石油工业出版社, 2008.

[19] 李利敏, 闫金鹏. 在校大学生肩宽及疏散速度的测量研究[J]. 工业安全与环保, 2014(11):44-47.

LI Limin, YAN Jinpeng. Measurement and analysis on shoulder width and evacuation speed of male college students[J]. Industrial Safety and Environmental Protection, 2014(11):44-47.

[20] CHEN Junmin, LIU Rong, WANG Jianyu, et al. Experimental influence of pedestrian load on individual and group evacuation speed in staircases[J]. Fire Technology, 2017, 53(5): 1745-1763.

[21] SEIKE M, KAWABATA N, HASEGAWA M. Evacuation speed in full-scale darkened tunnel filled with smoke[J]. Fire safety journal, 2017(91): 901-907.

[22] YU Wenjian, JOHANSSON A. Modeling crowd turbulence by many-particle simulations[J]. Physical Review. E, Statistical, Nonlinear, and soft Matter Physics, 2007, 76(4):1-5.

[23] LAKOBA T I, KAUP D J, Finkelstein N M. Modifications of the Helbing-Molnár-Farkas-Vicsek social force model for pedestrian evolution[J]. Simulation Transactions of the Society for Modeling & Simulation International, 2005, 81(5):339-352.

[24] 单庆超, 张秀媛, 张朝峰. 社会力模型在行人运动建模中的应用综述[J]. 城市交通, 2011, 9(6):71-77.

SHAN Qingchao, ZHANG Xiuyuan, ZHANG Chaofeng. A review of application of social force model for pedestrian dynamics[J]. Urban Transport of China, 2011, 9(6):71-77.