自动变速器传递误差的多目标优化方法

苏成云，王书翰，苑衍灵，李卫强，徐向阳1,

(1. 北京航空航天大学 交通科学与工程学院，北京 100191；2.国家乘用车自动变速器工程技术研究中心 盛瑞工程技术研究院，山东 潍坊 261205)

随着社会技术的进步和人们对整车舒适性的要求，自动挡汽车越来越多地进入人们的生活，与此同时，自动变速器齿轮的啸叫问题也更加引起重视. 微观修形是解决啸叫问题的重要手段，目的是降低其振动传递误差. 国外单纯通过降低传递误差来降低噪音水平的研究文献较多[1-2]，国内张标、顾廷昶、沈云波等通过抛物线修形的方法来对静态传递误差进行设计[3-5]. 但自动变速器由于自身结构的原因，单对啮合齿轮要同时参与多个挡位的动力传递，单一的优化方法很难得到最优解，或者没有进行灵敏度分析. 本文提出一种专门的优化方法来对特定的齿轮传动系统进行多工况多目标的优化设计.

1 静态传动误差

静态传递误差是指从动轮实际啮合位置与理论啮合位置在啮合作用线上的差值， 它是衡量齿轮副动态性能的一个重要参数，也是导致齿轮箱振动噪音的根本原因.

理论上齿轮传动关系为

(1)

但实际轮齿传动过程中，轮齿到达的位置与理论计算值相比时前时后. 将传动误差以齿轮2相对齿轮1的旋转角度偏差来表示时

(2)

为了方便描述，传递误差表示为

TEs=-Δθ2Δrb2=Ef1+Ef2+ESAB-

DB1+DB2+DH1+DH2

(3)

包含了齿形偏差和齿距偏差的轮齿综合偏差为

E=Ef1+Ef2+ESAB

(4)

定义轮齿的综合变形为

δ=DB1+DB2+DH1+DH2

(5)

而轮齿的综合变形又可表示为

δ=FN/kt

(6)

式中:FN为分度圆节点上的法向力;kt为啮合刚度.因此静态传递误差为

TEs=E-δ

(7)

2 不同优化方法比较

如表1所示为一自动变速器齿轮在不同工况下的动力传递情况. 其在所有挡位传递功率，如果对该齿轮的传动误差进行优化设计，则需要同时考虑8个工况.

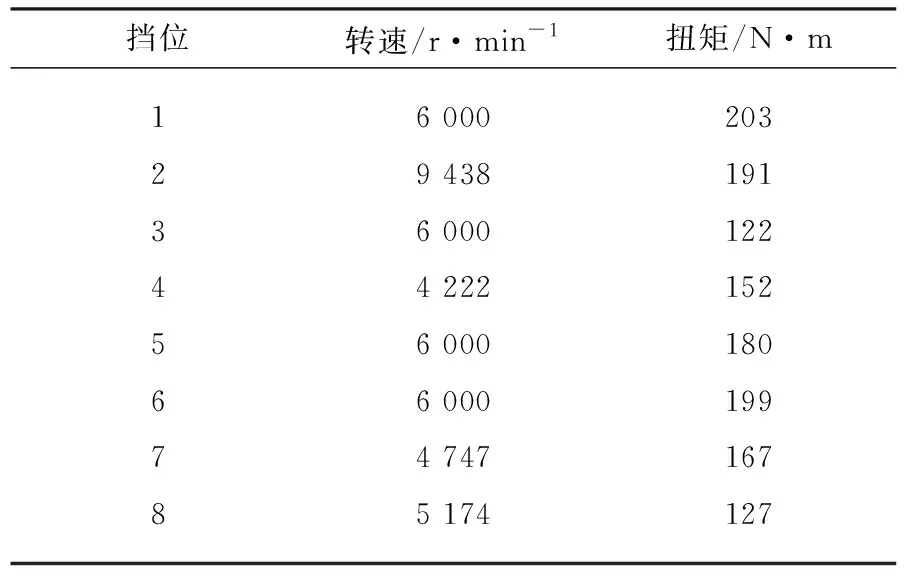
表1 齿轮副的不同工况动力传递Tab.1 Power route of gear pairs in different working conditions

若以各相关挡位传动误差的和值最小作为优化目标，可能会陷入局部最优解. 本文以Romax为工具，分析4种优化方法对寻求最优解的差异性，并最终得到一种最合适的优化方法.

2.1 全因子设计研究

全因子设计是将每个自变量的每一个工况做相同数目的计算. 该优化设置有5个自变量，每个自变量取4个工况，那么该优化过程需要仿真的次数为4^5(次).

该优化方法的自变量取值为各个自变量的自由组合，可用于初步缩减自变量域的范围，但对寻求最优解无针对性. 如图1所示为全因子设计方法的寻优规律，目标函数呈现点集现象，即只要自变量确定，不论重新优化多少次，得到的最优解都是一致的.

图1 全因子设计方法寻优规律Fig.1 Optimization rule with full factorial method

2.2 蒙特卡罗设计研究

蒙特卡罗设计主要通过大量的随机实验来获得最优解. 每个自变量的取值仅参与一次优化，自变量的数量和优化迭代次数一致.

该优化方法对每一个自变量选择一定数量的随机数值，后对各自变量进行自由组合，寻得最优目标函数. 该方法迭代速度较快，能够迅速确定多个优化区域，但是优化程度不深，适合优化初期的实验设计. 蒙特卡罗设计方法的寻优规律如图2所示.

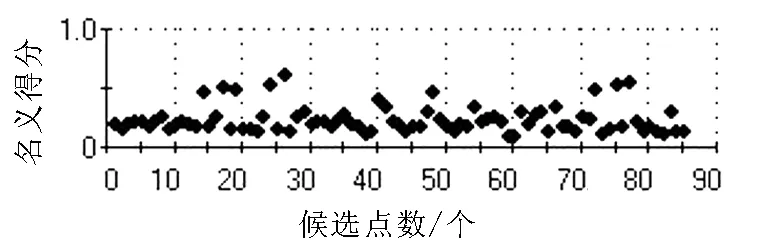
图2 蒙特卡罗设计方法寻优规律Fig.2 Optimization rule with Monte Carlo method

2.3 遗传算法

遗传算法各代之间没有明显的间隔，随着仿真次数的增加，目标函数平均值逐渐趋向最优解，且无用解的个数越来越少. 每次仿真完成后选择上一代最满足最优解的数据突变25%遗传给下一代，然后再将上一代数据自由组合25%繁殖给下一代. 剩下50%左右的数据则从原始数据中自由组合产生. 按照这样的规则，连续繁殖10代.

这种优化方法以寻求最优解为优化目标，基本能够得到合适的目标函数，但每一次遗传不能够保持原始数据的纯洁性，即容易偏离原始数据，引起发散. 普通遗传算法的寻优规律如图3所示.

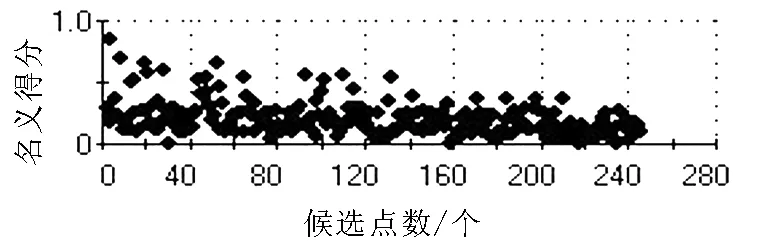
图3 普通遗传算法寻优规律Fig.3 Optimization route with genetic algorithm method

2.4 Romax高级遗传算法

高级遗传算法有明显的特征，上一代与下一代之间界限清晰，总体而言，下一代的数据总是更加接近最优解.

每次仿真完成后选择上一代最满足最优解的数据突变30%遗传给下一代，然后再将上一代数据自由组合20%繁殖给下一代. 为了保证种群最优解的优势，将上一代中不超过10%的最优解直接遗传给下一代，剩下的40%左右的数据则从原始数据中自由组合产生.高级遗传算法的寻优规律如图4所示.

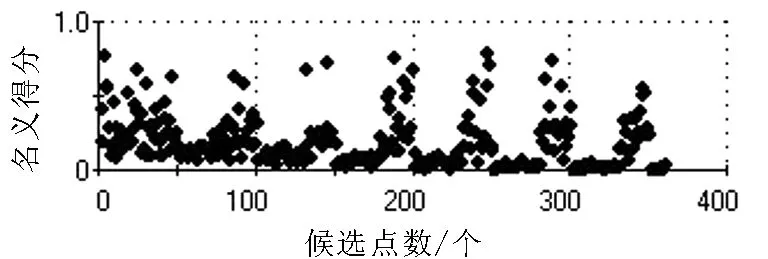
图4 高级遗传算法寻优规律Fig.4 Optimization route with genetic algorithm v2 method

这种优化方法以寻求最优解为优化目标，基本能够得到合适的目标函数,优点是在整个遗传过程中保持了原始数据的纯洁性，数据越大，越能够得到最优解；缺点是该最优解受第一代数据的影响比较大，而且第一代数据很容易陷入局部最优解，所以最终的优化结果无论是不是全局最优解，仍要进行稳健性分析，以确定该计算最优解的实用性.

2.5 4种优化方法对比

4种优化方法的对比及说明见表2.

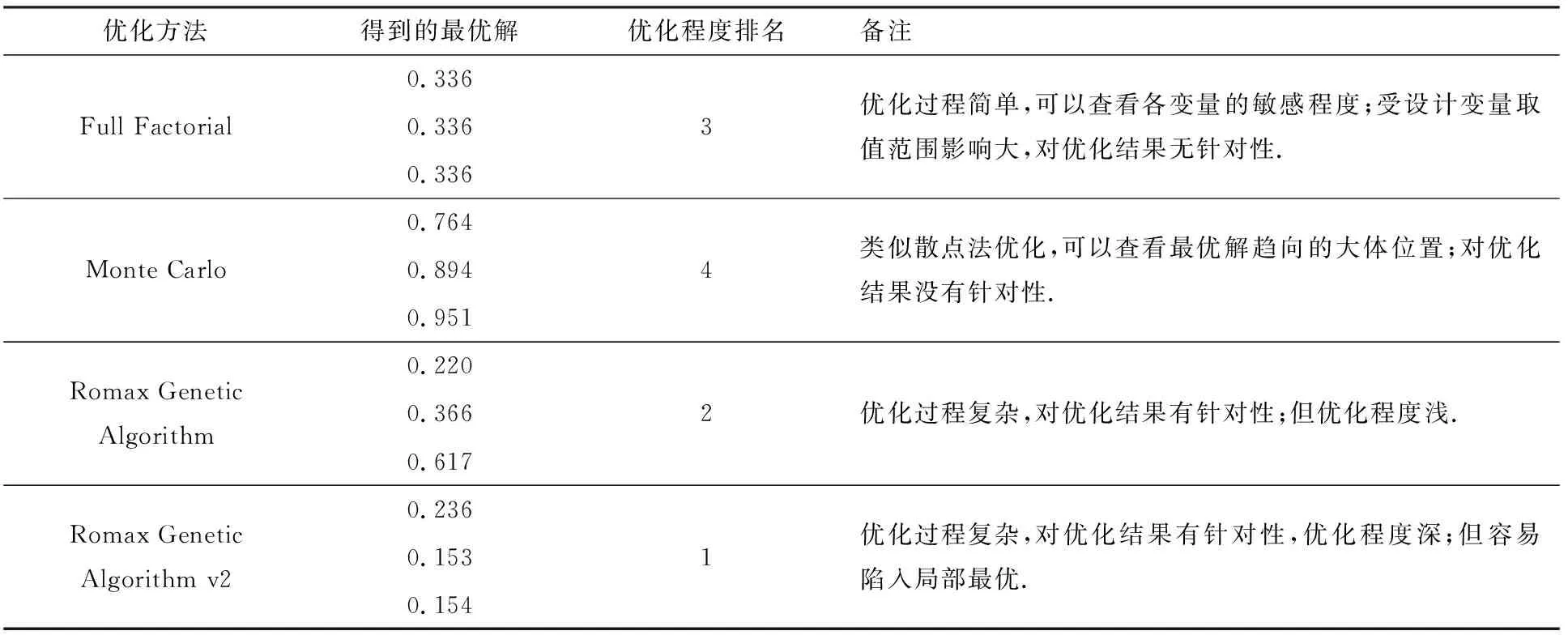
表2 4种优化方法对比及说明Tab.2 Comparison of the four optimization methods

3 优化流程的建立

在实际优化过程中，因为数据过于庞大，不能够仅利用上面的任何一种方法进行寻优的计算. 优化方法中2.1、2.2属于设计研究(Design Study)的范畴，可以借助其优化速度快的特点进行自变量域的缩减. 高级遗传算法优化较慢，但计算准确，优化程度深，可以用其针对某一自变量域进行深度优化. 另外，为了保证优化结果的稳健性，需要额外进行灵敏度分析，具体优化流程如下.

3.1 试验设计阶段

试验设计(Design of Experiment, 简称DOE)指的是通过少量的试验次数获得相对准确的自变量范围.通过以上两个设计研究方法对全流程的优化结果可知，全因子设计研究相较于蒙特卡罗方法能够得到更好的优化结果，故可以根据该优化结果重新设计所有设计变量的取值范围，以更加准确迅速地得到最优解.

表3 重新评估后的自变量取值范围Tab.3 Redefined range of variables

由表3可以看出，经过全因子设计后的自变量数据的范围得到明显的缩小，各变量范围都能控制在3μm以内,这对在同样自变量密度下取得最优解是很有帮助的.

3.2 优化设计阶段

上述分析可知，高级遗传算法较之普通的遗传算法能更顺利地得到最优解，所以在该优化流程中选择高级遗传算法进行目标函数的优化(见表4).

通过以上最后的几次优化,得到啮合齿轮的最佳修形量之和见表5(其中修形范围按照DIN3962标准设置).

表4 遗传算法最优解Tab.4 Optimal solution of genetic algorithm

表5 最终修形数值Tab.5 Final micro-modification μm

3.3 灵敏度分析阶段

该灵敏度分析在最优解已确定的条件下,研究其受哪些齿形齿向参数的影响波动较小，从而可以适当地调整该参数的修形范围. 这不仅可以降低不必要的加工精度，在时间和经济成本上也有一定帮助. 灵敏度分析结果见表6.

表6 灵敏度分析结果Tab.6 Results of sensitivity analysis

鼓形量参数对静态传动误差的灵敏度要小于倾斜修形参数. 另外，Cα和fHα的灵敏度小于标准值1，所以可以适当增加其自变量域的范围.同样地，要对Cβ和fHβ的标准适当加严. 优化流程如图5所示.

图5 优化流程图Fig.5 Flow chart of optimization

4 结束语

本文通过对比4种优化方法的传递误差结果，设计了适用于多目标多工况的传递误差优化分析方法. 在DOE数据设计的基础上进行优化设计，可以减小优化范围，便于获取最优解；优化完成后进行灵敏度分析，可以避免陷入局部最优解. 该流程方法同样适用于同类变速器齿轮的优化设计，具有理论参考和实践指导意义.

[1]LEE W Y, MOON K H, LEE D H. Characteristics of transmission error and vibration of broken tooth contact[J]. Journal of Mechanical Science & Technology, 2016, 30(12):5 547-5 553.

[2] YAKUPOV R R,MUSTAFIN T N, NALIMOV V N, et al. Analysis of transmission error depending on compressor working conditions[J]. Proceedings of the Institution of Mechanical Engineers, 2015, 229(2):122-129.

[3] 张标, 郭应清, 李丹. 变速箱齿轮修形设计方法研究[J]. 机械工程师, 2017(2): 138-140.

[4] 顾廷昶. 汽车变速器齿轮传递误差的研究及优化[J].传动技术, 2014, 28(4): 42-46.

[5]沈云波, 方宗德, 赵宁, 等. 斜齿面齿轮齿宽的设计[J]. 航空动力学报, 2008, 23(4): 754-758.