基于近场声全息技术的城市轨道交通列车车内声源识别研究

郭建强，孙召进，朱雷威，宋雷鸣

（1.中车青岛四方机车车辆股份有限公司 国家高速动车组总成工程技术研究中心，山东 青岛266111；2.北京交通大学 机械与电子控制工程学院，北京 100044）

0 引言

城市轨道交通由于其方便、快捷、高效等优点，成为目前大中城市发展公共交通的首选[1-2]。与此同时，城市轨道交通的一些弊端如噪声污染问题也随之显现，城市轨道交通车辆及设备运行中产生的高强度噪声会沿着固体物、空气等介质进行传播，对乘客的生理、心理造成严重干扰。在欧美等西方发达国家，重点关注的是城市轨道交通车辆运行环境噪声，并将其列为七大环境公害之一[3-5]。

随着城市轨道交通车辆制造水平的逐渐提高，在严格要求行车安全指标的同时，车内噪声评价已经成为城市轨道交通车辆的一项重要指标。为了控制噪声，国内外各车辆制造商纷纷加大了财力、人力及技术的投入。从噪声的特性产生、传播及影响特性出发，从 3 个方面进行噪声控制，即控制噪声源大小；干扰或阻断噪声的传播；保护噪声接受者。其中，最根本也是最有效的控制手段就是对噪声源进行控制，可以从根源上解决噪声污染问题。噪声源识别是对噪声源进行研究和控制的关键步骤，可以根据识别结果对整个噪声场进行重构，进而获得声辐射特性。在工程实践中，如表面振速法和近场声压法之类的早期声源识别方法，都是通过声、振动传感器进行简单的试验测量并对结果判断分析，实际精度不高。随着计算机技术的高速发展和信号处理技术的不断突破，相干分析、相关分析、频谱分析等新技术被陆续引入到噪声源识别领域中，形成了如波束形成、小波分析、声全息、声强测量等声源识别的新方法、新技术[6]。作为一种在近些年才发展起来的有效的噪声源识别技术，近场声全息可以为工程技术人员提供全面而丰富的声源和声场信息，从而为产品的低噪声设计、噪声控制提供参考。

1 近场声全息算法原理

近场声全息声场空间算法是近场声全息理论的发展重点，它是实现近场声全息的关键所在，也是沟通重建结果与全息面上测量数据的桥梁。目前近场声全息技术中已经发展出多种适用于不同声场的空间变换算法，因而找出适用于车内声场的近场声全息空间变换算法十分必要。近场声全息算法的核心思路是：测得声源近场全息面上的复声压，再运用傅里叶变换，将其从空间域转换到波数域，通过传递算子 G，使重建面 (源面或预测面) 接收到全息面信息，最后用傅里叶逆变换获得重建面上的质点振速或复声压。近场声全息算法原理流程图如图 1 所示。

图 1 近场声全息算法流程图Fig.1 Flow chart of NAH

根据理想流体媒质假设中小振幅声波的波动方程，可以得到稳态声场的不依赖时间变量的Helmholtz 方程[7-8]为式中：p (x，y，z) 代表空间点的复声压，是直角坐标的函数；k = ω / c = 2π / λ 为声波数，其中 ω 为角频率；c 为声音传播速度；λ 为特征波长。

设 pD，N(x，y) 为公式 ⑴ 的平面边界条件，根据格林公式可以求出公式 ⑴ 的解，即在 z＞0 的空间内，任意一点 (x'，y'，z') 声压为

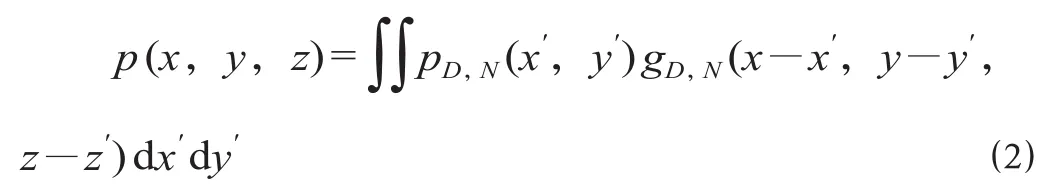
式中：gD，N(x－x'，y－y'，z－z') 为无限大平面的格林函数，gD(x－x'，y－y'，z－z') = z (1－ikr) eikr/2πr3，gN(x－x'，y－y'，z－z') = ieikr/ 2πr，其中 i 为虚

Neumann 边界条件的形式为 pN(x，y，z) = i∂p(x，y，z) / ∂z |z=0，该边界条件二维傅里叶变换 PN(kx，ky) 与 z = 0 平面上质点法向振速的二维傅里叶变换V (kx，ky) 关系为 PN(kx，ky) = V (kx，ky) ρ0ck。其中，ρ0为声介质的平均密度。

将公式 GD(kx，ky，z) = eikzz，GN(kx，ky，z) =eikzz/ k，PN(kx，ky) = V (kx，ky) ρ0ck 代入公式 P (kx，ky，z) = PD，N(kx，ky) GD，N(kx，ky，z) 后可以拆分为P (kx，ky，z) = PD(kx，ky)eikzz和 P (kx，ky，z) = V (kx，ky) ρ0ckeikzz/ kz。2 个公式对于 z = zH和 z = zS的任意 2 个平面，可以建立关系式为 P (kx，ky，zH) = P (kx，ky，zS) eikz(zH－zS) 和 P (kx，ky，zH) = V (kx，ky，zS)ρ0ckeikz(zH－zS)/ kz。已知 z = zS平面的声压或质点法向振速可以预测出更远处的 z = zH的声压情况，通过欧拉公式可以很方便地推出 z = zH面的微粒法向振速，由此，可以进一步地导出二阶声场参量声强及远场的指向性等；当已知 z = zH的声压数据可以反演更近表面 z = zS(重建面) 的声压和质点法向振速。此时，可以得到平面近场声全息重建的基本公式为P (kx，ky，zS) = P (kx，ky，zH) e－ikz(zH－zS)和 V (kx，ky，zS) = kzP (kx，ky，zH) e－ikz(zH－zS)/ ρ0ck 。

为了验证基于平面的近场声全息理论及算法的正确性，对该算法进行编程，通过采用实验验证该算法及程序的正确性。

2 城市轨道交通车辆内部声全息扫描分析

2.1 实验室验证与分析

在城市轨道交通车辆验证试验之前，在实验室内 (消声室和混响室) 对噪声源进行了识别试验，以验证近场声全息技术对车内混响场中声源的识别能力。声源为实验室支架上布置的 2 个扬声器，地面距声源中心 1.4 m，两声源中心相距 0.23 m。8×8 个测点均匀分布在全息面上，声源前表面与全息面相距 0.07 m，全息面中心正对两声源连线的中心。因此，地面距离全息面中心也为 1.4 m。该实验分消声室和混响室 2 次进行，2 次声源的发声频率分别为 1 000 Hz、1 500 Hz。

在消声室中，分别进行 1 000 Hz 的双声源识别和 1500 Hz 的双声源识别验证实验，由实验结果可知，在声源近场，从声源面的声压级分布可以清楚地识别双声源的位置，与实际声源摆放的位置基本吻合，双声源周围声压级的幅值变化趋势明显，且两声源的声压级与实际声源的幅值相当，两声源幅值之间或峰值周边无明显的旁瓣，这说明在理想条件下，该技术可较好地对多声源进行识别。由于实车车内声场的复杂性，消声室并不能很好地模拟车内的实际情况。

混响室比消声室的声场条件要复杂得多，对近场声全息技术的验证更接近实际。在混响室中，同样进行 1 000 Hz 的双声源识别和 1500 Hz 的双声源识别验证实验。测试结果可知，噪声最大值主要集中在双声源附近，即在阵列架的测试范围内，可以准确判断声源的具体位置，双声源周围无明显次级声源干扰，声源大小与实际相当，声源识别效果良好，从而能够有效保证实车测试结果的准确性。

在实验室状态下验证了近场声全息技术声源识别准确性后，对某地城市轨道交通车辆内部进行声全息扫描分析，在测试过程中对测试结果产生影响的车内广播、车载空调均关闭，车外设备处于正常工作状态。首先，运用该方法对车内噪声源进行识别，取得车体结构的主要噪声透射点；其次，对列车匀速运行过程中车内漏声点处的噪声进行分析，应用声全息阵列对某城市轨道交通列车 2 车一侧侧墙 1 门到 3 门之间的区域进行扫描，运行速度重点考核 60 km/h，80 km/h；第三，评价车内侧不同区域漏声对车内噪声的影响，为车内噪声控制提供参考。车内噪声声全息扫描示意图如图 2 所示。

2.2 车内噪声水平分析

图 2 车内噪声声全息扫描示意图Fig.2 Diagram of acoustical holography scanning of interior noise of train

在进行车内声全息实验之前，为了更好地把握列车内部真实噪声环境的具体频率分布，为下一步确定声全息阵列架的采集频率范围有重要借鉴和参考意义。对城市轨道交通车辆内部采集的噪声信号做相应频谱分析，以期了解到车内噪音具体的分布频率范围。现对城市轨道交通车辆在 60 km/h、80 km/h 2 个匀速速度级做相应的频谱分析。60 km/h列车中部噪声测点 1/3 倍频程图如图 3 所示，80 km/h列车中部噪声测点 1/3 倍频程图如图 4 所示。图 3 和图 4 分别给出了列车内中部噪声测点在匀速 60 km/h和 80 km/h 工况下的列车中部噪声测点 1/3 倍频程图。从图中可以看出 2 个速度级下列车内噪声的主要频率集中在中高频段，在 800 Hz 出现峰值，低频段噪声对车内噪声的贡献较低。

图 3 60 km/h 列车中部噪声测点 1/3 倍频程图Fig.3 A third octave of vehicle center point at 60 km/h

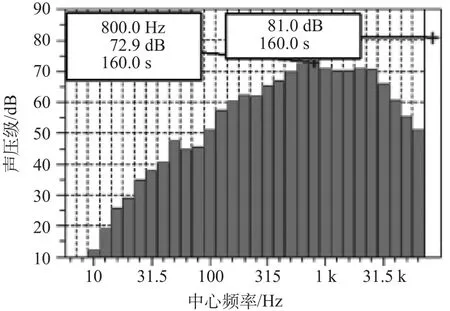
图 4 80 km/h 列车中部噪声测点 1/3 倍频程图Fig.4 A third octave of vehicle center point at 80 km/h

2.3 车内声全息扫描测试结果分析

通过对城市轨道交通列车车内声全息扫描测试分别得到了列车以 60 km/h 和 80 km/h 速度匀速运行时车内侧墙全频域 (100-6300 HZ) 1/3 倍频程近场声全息扫描结果图和 60 km/h、80 km/h 速度级声全息车内扫描结果，由车内声全息扫描测试结果可知，噪声源的声辐射区域主要集中在车门下半部分与地板连接缝隙处、车门上部中间区域、车窗的中部及周边区域、侧墙与顶部车体区域的连接处缝隙、侧墙与车门连接的缝隙、座椅的上部与侧墙的连接区域等，车内漏声点主要分布在车门与周边部件连接的缝隙处，以及车窗周边区域；车窗的边沿有漏声情况，但不是噪声的主要来源。车内漏声最严重的区域位于是车门缝隙处，A 声压级噪声值大约为 90 dB。车窗区域的A 声压级噪声值为 85～88 dB，车门和其他区域的噪声辐射状况相对良好，A 声压级噪声值均在 85 dB以下，这其中的部分区域 A 声压级噪声值大小在81 dB 以下，说明位于该区域的车体密封性和车体振动情况相对较好。对比 2 个速度级下列车车门的声辐射情况，不难看出声辐射较为突出的部位位于车门的下半部分的边缘缝隙，这是由于该区域不仅受列车运行时的气动声影响，同时也有来自轮轨区域的辐射。车窗周围的声辐射状况相对于座椅上方的侧墙而言更为突出。

3 结束语

精确识别城市轨道交通列车车内噪声源是进行城市轨道交通列车减振降噪的重要依据，能够合理可靠地提升列车乘坐舒适度，提高乘客乘坐满意度，从而提升我国城市轨道交通列车的市场竞争力。从理论及工程实践角度，将平面声全息技术应用于城市轨道交通列车车内噪声源识别，有助于充分考虑多种因素的影响与列车在运行工况下车内噪声源的变化特点，进而更加准确的识别城市轨道交通列车车内的噪声源。此外，对于近场声全息算法编写的程序而言，由于数据量大，并且程序开放性不够，数据的分段处理及格式转换等过程较为繁琐，可通过对程序的进一步优化，提高处理软件的模块化和集成化，进而提高工作效率。

[1] 刘英杰. 地铁车站噪声测试与分析[J]. 铁道标准设计，2009(8)：110-114.LIU Ying-jie. Tests and Analysis on Noises at Metro Stations[J]. Railway Standard Design，2009(8)：110-114.

[2] 黎 林，王晋强，田 钊，等. 城市地铁商铺租金定价方法的研究[J]. 铁道运输与经济，2017，39(2)：16-21.LI Lin，WANG Jin-qiang，TIAN Zhao，et al. Study on Rent Pricing Method of Commercial Premises in City Metro[J].Railway Transport and Economy，2017，39(2)：16-21.

[3] 宋 晶，郝 珺. 地铁车站对周围环境振动与噪声的影响分析及对策[J]. 城市轨道交通研究，2008，11(3)：26-29.SONG Jing，HAO Jun. Influence of and Countermeasures Against Vibration and Noise Pollution of Metro Station[J].Urban Mass Transit，2008，11(3)：26-29.

[4] JIAN Han，XIN Biao-Xiao，YUE Wu. Effect of Rail Corrugation on Metro Interior Noise and Its Control[J].Applied Acoustics，2017(11)：63-70.

[5] 郝艳华. 铁路货运中心客户关系管理的探讨[J]. 铁道货运，2016，34(7)：29-32.HAO Yan-hua. Discussion on Customer Relationship Management of Railway Freight Transport Center[J]. Railway Freight Transport，2016，34(7)：29-32.

[6] 陈心昭，毕传兴. 近场声全息技术及其应用[M]. 北京：科学出版社，2013.

[7] 杨德森，郭小霞，时胜国. 基于振速测量的 HELS 方法研究[J]. 哈尔滨工程大学学报，2011，32(5)：618-623，671.YANG De-sen，GUO Xiao-xia，SHI Sheng-guo. Experimental Research on Reconstructing an Acoustic Field Using the Hels Method with the Measurement of Particle Velocity[J]. Journal of Harbin Engineering University，2011，32(5)：618-623，671.

[8] 于 飞，陈 剑，李卫兵，等. 声场分离技术及其在近场声全息中的应用[J]. 物理学报，2005，54(2)：789-797.YU Fei，CHEN Jian，LI Wei-bing，et al. Sound Field Separation Technique and Its Applications in Near-Field Acoustic Holography[J]. Acta Physica Sinica，2005，54(2)：789-797.