可变编组条件下的城市轨道交通大小交路优化研究

方开莎，董奇志，牛红霞

（1.河南交通职业技术学院 轨道交通学院，河南 郑州 450000；2.郑州铁路职业技术学院 科研外事处，河南 郑州 451460；3.郑州铁路职业技术学院 交通运输系，河南 郑州 451460）

0 引言

城市轨道交通运输组织以客流需求为导向，组织列车运行通常采取平行图、单一交路、编组固定模式，根据全线最大客流断面数据确定列车的发车频率。由于城市发展的不均衡性和客流 OD 的离散性，城市轨道交通断面客流具有时间和空间上的波动性[1]。在此情况下，单一交路模式无法考虑客流断面的离散性，造成郊区列车满载率低、运能浪费，而中心城区列车满载率过高、运能不足的情况，使得全线的服务质量受到影响[2]。针对这样的问题，通过改变单一交路运营模式，根据断面客流差异采取大小交路的运营模式，充分发挥列车输送能力，有利于运力资源的优化配置，满足不同区段客流的需求。

针对断面客流不均衡条件下城市轨道交通大小交路开行方案研究，孙焰等[3]以列车满载率最大及运营时段数最少为目标，构建班次优化模型，求解线路存在多个循环区段条件下的车底运用数下界。王媛媛等[4]考虑乘客出行成本及企业运营成本最小化，构建模型优化大小交路模式下的列车开行方案。Paolo 等[5]以乘客出行成本和企业运营成本最小化为目标，研究车型、发车频率和行车间隔的优化问题。徐瑞华等[6]从服务水平、列车运用及客流组织等方面入手，分析不同交路条件下的运输组织特点，提出市域轨道交通运输组织的基本原则。李素莹等[7]分析了上海轨道交通 1 号线大小交路运营的经验。

目前针对城市轨道交通大小交路运营相关问题的研究，通常未考虑列车编组可变，可以从交路区段、开行频率 2 方面进行运行方案的优化，在此情况下，当小交路外围区段的断面客流量较小时，为保证小交路区段列车的满载率不致过低，不可避免地会增加小交路区段发车间隔时间，从而延长小交路区段乘客的等待时间，降低服务水平。针对此问题，考虑不同交路的列车编组可以根据客流情况灵活改编，从而平衡小交路区段列车满载率与列车发车间隔之间的矛盾，提高小交路区段的服务水平。城市轨道交通运营的网络化发展，对运营模式提出了新的挑战，国内外诸多城市开始研究多编组和灵活编组的运营方式[8-9]。其中，法兰克福地铁采用了不同编组混跑的运营组织模式，取得了较好的效果[10]。因此，在不同交路列车可以采用不同编组的前提下，针对城市轨道交通大小交路组织问题，根据运营需求构建大小交路列车开行方案优化模型，对城市轨道交通大小交路列车开行方案进行优化。

1 城市轨道交通大小交路优化模型构建

1.1 问题提出

假设城市轨道交通采取单线路独立运营，考虑某线路沿线共有 N 座按顺序编号的车站，记 1 至 N 站方向为该线路的上行方向，有 d = 1；反之为下行方向，有 d = 2。大交路列车运行区段为 1 至 N 站；小交路列车运行区段为 S0至 S1站。大小交路列车的开行频率、列车编组分别记为 f1及f2、n1及 n2，其中大小交路列车共线运行的区段记为 M2，其他区段记为 M1。大小交路区段示意图如图 1 所示。

图 1 大小交路区段示意图Fig.1 Locations of the different routings

城市轨道交通大小交路开行方案的关键是根据客流分布情况，协同优化小交路折返站及大小交路列车编组，应尽量使乘客的出行及企业运营成本最小化，以满足乘客出行对服务质量的要求，以及城市轨道交通运营企业的经济性要求。基于上述考虑，通过构建模型对大小交路开行方案进行优化。假设条件为：①乘客在各站均匀到达，并且到站乘客在站均能登上第一趟直达列车，不考虑乘客滞留情况；②交路重合区段大小交路列车间的乘客分担比例由对应交路列车的开行频率决定；③大小交路列车的编组情况可以根据客流灵活改变；④大小交路列车的车底运用相互独立，互不嵌套；⑤沿线各站均具备列车折返条件；⑥列车运行速度相同，不考虑小交路列车折返作业对大交路列车运行的影响。

上述假设不影响模型的适用性，并且能够在一定程度上简化建模及求解过程。

1.2 参数说明

模型参数说明：λkl为在第 k 站上车、第 l 站下车的乘客人数；(l1，l2) 为在第 k 站上车、第 l1和 l2站间下车的乘客人数，上行方向列车，在第 k 站上车，在第 k + 1 站和第 N 站之间下车的乘客人数，有为乘坐下行方向列车，在第 k 站上车，在第 1 站和第 k－1 站之间下车的乘客人数，有列车交路字典，当 h = 1 时表示大交路，h = 2 时表示小交路；nh为担当交路 h 的列车编组；v 为列车折返时间；Lh,d为交路 h 在 d 方向的长度；Vd为列车在 d 方向的旅行速度；ti为第 i 个运营时段的时长；f0为最小发车频率；fm为线路最大通过能力；nm为列车最大编组辆数；Nh为交路 h 所需车辆数；No为最大车辆运用数；ηh为示交路 h 的最大断面满载率；ηm为列车最大满载率；r 为相邻站站间区间；Rh为交路 h 所经区间集合；C 为车辆定员；Qh,r为交路为 h 的列车在第 r 个区间上所分担的断面客流量；qOD为 OD 度客流的需求；M1,r为乘坐大交路列车经过第 r 个区间的客流 OD 集合；M2,r为乘坐小交路列车经过第 r 个区间的客流 OD 集合。

1.3 目标函数

城市轨道交通系统的广义成本为优化目标，主要包括旅客出行成本和企业运营成本。旅客出行成本由乘客在站等待时间及乘车时间之和表示。由于城市轨道交通列车速度、停站时间均相同，乘客乘车时间与乘坐列车的交路情况无关，因而乘客出行成本主要受乘客在站等待时间影响。图 1 所示的开行大小交路运营模式下，M1区段内的乘客只能由大交路列车运输，乘客在站等待时间与大交路列车开行频率有关；而 M2区段内的乘客由大小交路列车运输，乘客在站等待时间与大小交路列车的发车频率均相关。假设乘客在站到达服从均衡分布规律，则乘客在站等待时间的期望即为发车间隔的一半，由此可得上行方向的乘客等待时间为

式中区段内的乘客等待时间；为 M2区段内的乘客等待时间。

同理，下行方向的乘客等待时间为

乘客在站等待时间最小化目标函数为

轨道交通企业的运营成本包括列车运行成本与人力成本。其中，列车运行成本受车辆走行公里影响；人力成本受列车运行时间影响。

列车运行成本最小化函数为

人力成本最小化函数为

1.4 约束条件

列车运输组织需要满足列车运输组织约束及客流需求的约束，充分利用线路能力，满足客流输送需求。列车运输组织约束条件如下。

（1）列车发车频率约束

（2）大小交路重合区段线路能力约束

（3）列车最大满载率约束

（4）列车最大编组约束

（5）全线车辆数约束

（6）小交路区段约束

客流需求约束为各站发车频率需与该站乘客输送量相匹配

上式中有

其中，

1.5 求解方法

公式 ⑶ 至公式 ⑿ 构成了一个多目标约束优化模型，需要将多目标转化为单目标处理，求解思想为：以线性加权方式将多目标模型转化为单目标模型；对原约束添加罚函数，并将原模型转化为无约束模型。根据上述公式，首先采用线性加权法将公式 ⑶ 至公式 ⑸ 转化为

式中：ω1，ω2，ω3为权重系数。

多目标模型中各目标的量纲不同，需要对多目标进行无量纲转化，其方法为：首先以列车开行单一交路的目标值为基准进行无量纲化处理，设 tw为乘客等待时间，Vkm为车辆走行公里，t0为列车运行时间，根据 Alejandro 等所给出的方法，计算 tw，Vkm及 t0，令 ω1tw= ω2Vkm= ω3t0，取 ω1= 1，求得 ω2=ω1tw/Vkm，ω3= ω1tw/t0[11]；然后对权重进行归一化处

在目标函数转化完成后，采用受控随机搜索算法即可对转化后的模型进行方便地求解。受控随机搜索算法是 1976 年由 Prince 提出的一种全局优化算法，适用于求解目标函数非可导、决策变量不连续的多变量组合优化问题，因而根据 Alejandro，Price等算法对城市轨道交通大小交路优化构建模型进行求解[11-12]。

2 实例验证

2.1 算例及参数设定

以某轨道交通线路为例，验证所构建模型的有效性。该线路共包含 30 个站、29 个区间，折返站为第 4 站和 22 站，各站台长度均满足 A 型车 8 辆编组停靠需要，因而不同交路列车可以采取不大于 8辆编组的编成模式，各区间长度如表 1 所示。选取工作日早/晚高峰 (8 : 00—9 : 00/18 : 00—19 : 00) 及平峰 (12 : 00—13 : 00) 3 个时段的客流数据验证模型有效性，早晚高峰、平峰断面客流量如表 2 至表 4 所示，模型参数设定如表 5 所示。

表 1 各区间长度Tab.1 Distances of the sections

2.2 计算结果

在给定参数下对不同时段的列车开行方案进行优化，由假设条件可以得知，最优开行方案与小交路列车的编组情况有关。为对结果进行比较分析，在计算过程中将大交路列车固定为 8 A 编组，针对小交路列车采用 6 A、8 A 编组的情形，分别测试。列车开行方案优化结果如表 6 所示。

算例中，城市轨道交通大小交路优化结果为早晚高峰时段采用大小交路混合模式；平峰时段采用单一交路模式。经计算，全线早、晚高峰时段断面最大客流量与最小客流量间的差值分别为 42 194 人及 36 212 人；而平峰时段全线的最大客流量断面仅为 10 181 人。由于高峰时段全线的断面客流量差值较大，采用大小交路模式更有利。

根据计算得到的列车开行方案及客流数据，统计不同交路模式下的车辆运用数及平均满载率，其中车辆运用数为列车编组与开行列车数的乘积。不同运输组织模式下列车运行指标如表 7 所示。

根据所得结果，可知不同编组及交路模式对列车开行方案指标的影响如下。

表 2 早高峰断面客流量Tab.2 Passenger volume during morning rush hours

表3 晚高峰断面客流量Tab.3 Passenger volume during night rush hours

表4 平峰断面客流量Tab.4 Passenger volume at normal time

表 5 参数设定Tab.5 Parameter setting

（1）全线列车均采用 8 A 编组时，早晚高峰时段的乘客等待时间指标出现增长；同时，车辆走行公里和车辆运用数指标出现下降。

（2）全线列车均采用 8 A 编组时，早晚高峰时段的目标函数值分别下降了 11% 和 7.8%。

（3）当大小交路列车分别采用 8 A 和 6 A 编组时，早晚高峰时段的乘客等待时间、车辆走行公里和车辆运用数指标均得到了优化，出现一定程度的下降。

表 6 列车开行方案优化结果Tab.6 Optimization of train plans

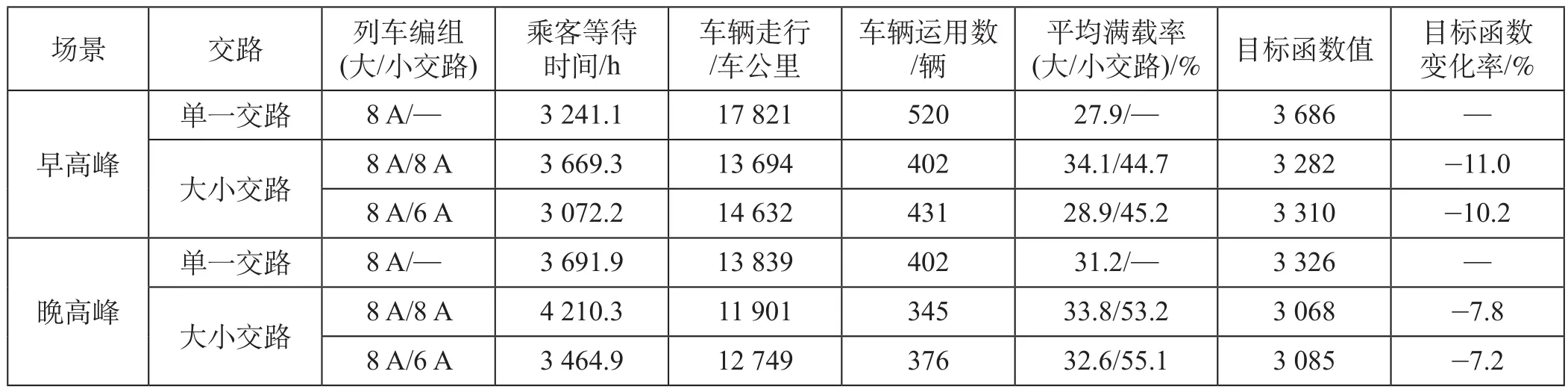
表7 不同运输组织模式下列车运行指标Tab.7 Indexes under different operational models

（4）当大小交路列车分别采用 8 A 和 6 A 编组时，早晚高峰时段的目标函数值分别下降了 10.2%和 7.2%；同时，小交路区段的列车发车频率分别从 8 对/h、4 对/h增加至 13 对/h、8 对/h。

根据上述分析可知，断面客流量存在明显差异的城市轨道交通线路，采用大小交路运营方式有利于改善服务水平、提高企业效益；大交路列车采用大编组、小交路列车采用小编组的模式更有利于乘客服务水平和企业效益的平衡，但会增加列车的运行数量。在算例中，由于乘客乘车需求低于线路运能，出现了平均满载率较高的情况，说明该线路运能仍然有富余。结果显示，采用大小交路模式提高了列车满载率，改善了列车满载率指标，避免运力浪费。

3 结束语

我国城市轨道交通正处于高速发展阶段，现有的固定编组运营模式在应对多样客流需求的灵活性上存在一定不足。强化客流需求导向的运输组织理念，根据实际客流需求采用可变编组的灵活运输组织方案，将有利于平衡乘客在站等待时间与车底购置费用等之间的矛盾，是城市轨道交通运输组织精细化、智能化的需要。同时，还能有效降低城市轨道交通运营成本，全面提高城市轨道交通运营组织水平。

[1] 陈胜波，何世伟，何必胜. 客流波动条件下城市轨道交通列车开行方案研究[J]. 城市轨道交通研究，2013，16(10)：53-58.CHEN Sheng-bo，HE Shi-wei，HE Bi-sheng. Train Service for Urban Transit with Passenger Fluctuation[J]. Urban Mass Transit，2013，16(10)：53-58.

[2] 李俊芳，王柄达. 城市轨道交通典型交路形式分析[J]. 铁道运输与经济，2009，31(10)：54-58.LI Jun-fang，WANG Bing-da. Analysis on Typical Routing Forms of Urban Rail Transit[J]. Railway Transport and Economy，2009，31(10)：54-58.

[3] 孙 焰，施其洲，赵 源，等. 城市轨道交通列车开行方案的确定[J]. 同济大学学报 (自然科学版)，2004(8)：1005-1008，1014.SUN Yan，SHI Qi-zhou，ZHAO Yuan，et al. Method on Making Train Running-plan for Urban Railway Traffic[J].Journal of Tongji University(Natural Science)，2004(8)：1005-1008，1014.

[4] 王媛媛，倪少权. 城市轨道交通大小交路模式列车开行方案的优化[J]. 铁道学报，2013，35(7)：1-8.WANG Yuan-yuan，NI Shao-quan. Optimization of Train Schedules of Full-length & Short-turn Operation Modes in Urban Rail Transit[J]. Journal of China Railway Society，2013，35(7)：1-8.

[5] PAOLO D S，FRANCESCO F. Service Optimization for Bus Corridors with Short-turn Strategies and Variable Vehicle Size[J]. Transportation Research Part A：Policy and Practice，1998，32(1)：19-38.

[6] 徐瑞华，李 侠，陈菁菁. 市域快速轨道交通线路列车运行交路研究[J]. 城市轨道交通研究，2006(5)：36-39.XU Rui-hua，LI Xia，CHEN Jing-jing. Optimization of Routing Mode on Regional Express Rail[J]. Urban Mass Transit，2006(5)：36-39.

(  )(  )

[7] 李素莹，陈光华，车永兵. 上海轨道交通1号线开行大小交路运行方案的实践[J]. 城市轨道交通研究，2007(1)：50-53.LI Su-ying，CHEN Guang-hua，CHE Yong-bing. Practical Analysis of Long & Short Routing Operation Mode for Shanghai Metro Line1[J]. Urban Mass Transit，2007(1)：50-53.

[8] 禹丹丹，韩宝明，张 琦，等. 基于灵活编组的轨道交通列车开行方案优化方法[J]. 北京交通大学学报，2015，39(6)：21-31.YU Dan-dan，HAN Bao-ming，ZHANG Qi，et al.Optimization Method for Train Plan of Urban Rail Transit based on the Flexible Length of Train Formation[J]. Journal of Beijing Jiaotong University，2015，39(6)：21-31.

[9] 雷晓瑜，杨国飞，易晨阳，等. 轨道交通灵活编组及其组合运输组织特点的探讨[J]. 铁道运输与经济，2015，37(9)：64-69.LEI Xiao-yu，YANG Guo-fei，YI Chen-yang，et al.Discussion on Flexible Formation of Rail Transit and Its Characteristics of Combined Transport Organization[J].Railway Transport and Economy，2015，37(9)：64-69.

[10] 王振海. 欧洲城市轨道交通及对中国的借鉴意义[J]. 地铁与轻轨，2003(5)：57-61.

[11] ALEJANDRO T，CRISTIAN E，SERGIO J D. Optimal Design and Benefits of A Short Turning Strategy for A Bus Corridor[J]. Transportation，2011，38(1)：169-189.

[12] PRICE W L. A Controlled Random Search Procedure for Global Optimization[J]. The Computer Journal，1976，20(4)：367-370.