基于带隙特性的周期性排桩隔振性能研究

张 冰，刘艳青，张胜龙,3，王文斌,3

(1.中国铁道科学研究院，北京 10081；2.铁科院(北京)工程咨询有限公司，北京 100081；3.中国铁道科学研究院 城市轨道交通中心，北京 100081)

随着城市轨道交通的快速发展和人们对生活质量要求的不断提高，城市轨道交通运营引起的近场建筑物的振动及噪声问题逐渐引起人们的关注[1]。为了缓解城市轨道交通引起的振动问题，根据周期性结构的带隙特性，对周期性排桩结构在城市轨道交通减振降噪领域的隔振性能进行了研究。

周期性结构的带隙特性可以用固体物理学中的声子晶体进行阐述，声子晶体[2-4]的基本特征就是它的禁带机理。声子晶体的出现使特定频段的减振隔振成为可能[5-6]，同时带隙特性使得周期性结构在减振降噪领域具有十分广阔的应用前景[7-11]。

本文以粉质黏土为基体材料、混凝土为散射体材料的周期性排桩结构为主要研究对象，用有限元法研究各材料参数对带隙特性的影响规律。

1 基于有限元法的带隙特性计算

1.1 带隙结构计算

在声子晶体研究中，有限元法可用于带隙特性和传输特性的计算[12-13]。利用有限元软件求解波动方程时，根据Bloch定理[4]，位移场u(r)可表示为

u(r)=ei(k·r)uk(r)

(1)

式中：uk(r)是与声子晶体周期性相同的周期函数；k为第一布里渊区内的波矢；r为位移矢量。

单胞离散形式的特征方程和边界条件分别为

(K-ω2M)U=0

(2)

U(r+a)=ei(k·r)U(r)

(3)

式中：ω为角频率；K为刚度矩阵;M为质量矩阵;U为位移矩阵;a为晶格常数矢量。

利用有限元软件COMSOL Multiphysics进行计算，用波矢k扫描结构的不可约布里渊区的高对称边界，联合求解式(2)和式(3)即可得到声子晶体的带隙结构。

1.2 周期性排桩布置形式

图1(a)为正方形周期性排桩截面图。图中正方形为原胞单元，周期常数为a，桩体的半径为R。定义桩体在原胞中占有的面积比为填充率ff=πR2/a2。如图1(b)所示为正方晶格第一布里渊区和不可约布里渊区(图中阴影部分)。

图1 正方形周期性排桩及布里渊区

1.3 周期性排桩带隙计算

对于二维二组元周期性排桩带隙进行计算时，选取桩体材料为素混凝土，土层为粉质黏土。材料物理参数见表1。

图2是排桩正方形布置时平面内模式的典型带隙特性图，图中曲线为一组结构本征频率随波矢的变化关系，频率范围50.2～57.0 Hz的阴影部分为完全带隙，宽度为6.8 Hz。

表1 材料物理参数

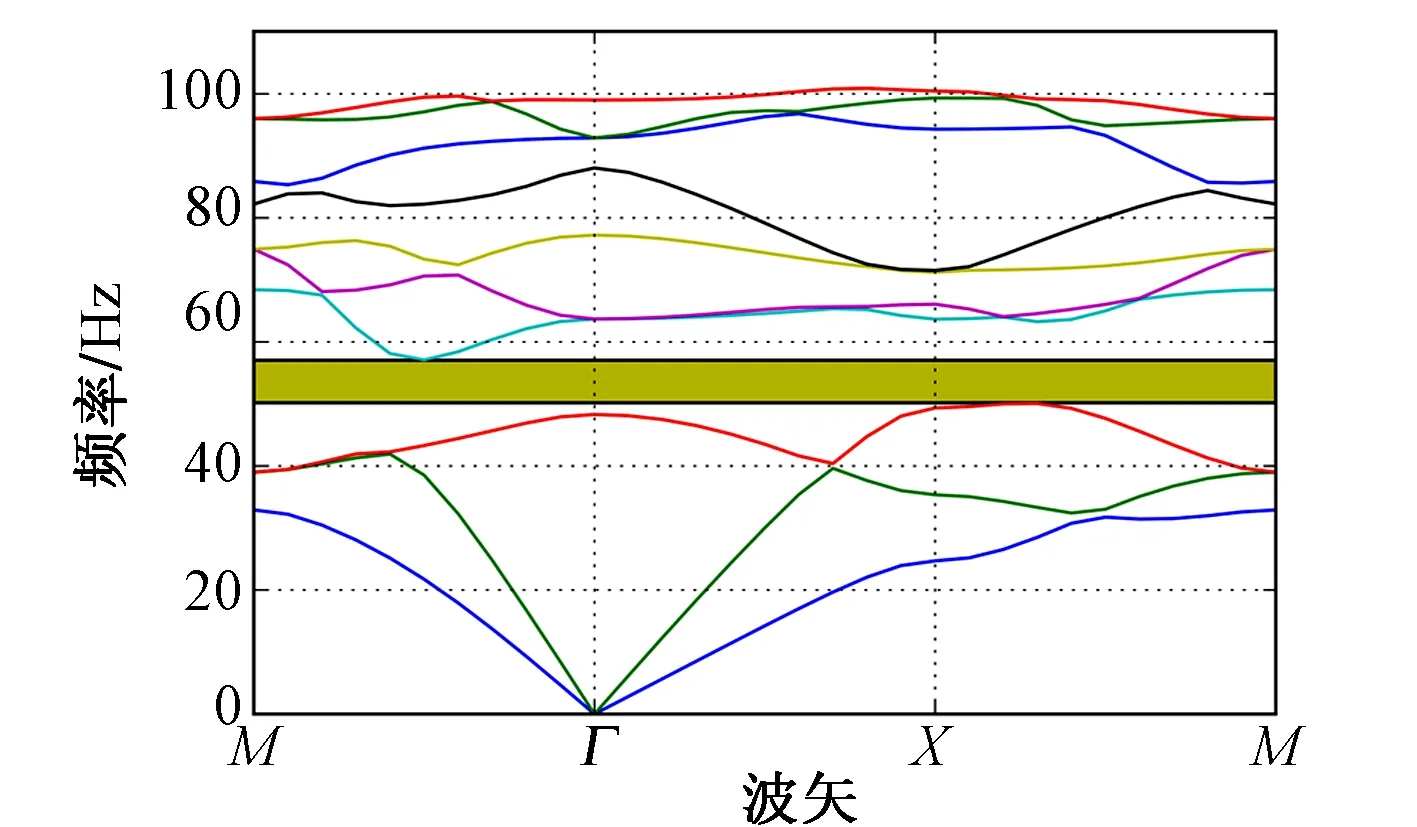
图2 周期性排桩带隙特性曲线

在完全带隙频率范围内的弹性波不能通过周期性排桩传播。因此通过合理设计排桩的物理参数和结构参数，可以调节完全带隙的位置和宽度范围，针对城市轨道交通振动的主要频率段布置具有工程应用价值的周期性排桩来实现减振隔振的目的。

2 周期性排桩影响因素分析

材料参数是影响周期性排桩带隙特性的主要因素。本节主要研究排桩正方形布置时的散射体和基体的物理参数(弹性模量、密度)、几何参数(填充率、周期常数)对带隙参数(起始频率、截止频率、带隙宽度)的影响。

2.1 散射体弹性模量和密度

散射体材料的弹性模量和密度对带隙的影响规律见图3。从图3(a)可以看出,带隙的起始频率、截止频率和带隙宽度随着散射体的弹性模量增加变化很小；从图3(b)可以看出,起始频率随着混凝土的密度的增加而减小，截止频率变化很小，带隙宽度随着密度的增加而增大。

图3 散射体材料对带隙特性的影响

2.2 基体弹性模量和密度

基体材料的弹性模量和密度对带隙的影响规律见图4。从图4(a)可知，带隙的起始频率、截止频率和带隙宽度随着基体材料的弹性模量增加而增大，且带隙频率变化较大；从图4(b)可知，截止频率随着混凝土的密度的增加而减小，起始频率变化很小，带隙宽度随着密度的增加而减小。

图4 基体材料对带隙的影响

2.3 填充率和周期函数

设定周期常数为定值，图5(a)给出了填充率和带隙之间的关系。可知，衰减域起始频率、截止频率和带隙宽度随着填充率的增加而增加。

选填充率为定值，周期性常数对完全衰减域的影响见图5(b)。可知，随着周期常数a的增加，带隙的起始频率、截止频率都迅速减小，带隙宽度缓慢减小。

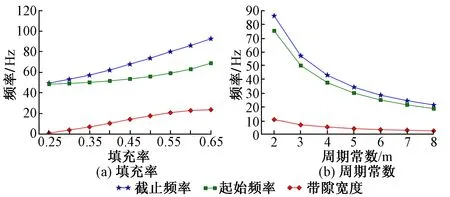
图5 填充率和周期常数对带隙的影响

3 振源振动加速度现场测试

3.1 现场测试

为了获得地铁列车通过时引起周围土层的振动特征频率，在北京市某运营地铁线路旁地表进行振动加速度现场测试。线路轨道形式为普通整体道床轨道，现场测点如图6所示。

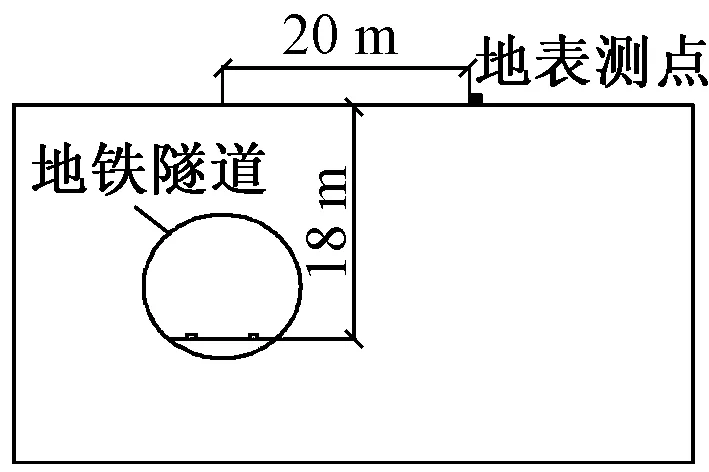
图6 地表振动加速度测点示意

地铁列车经过时地表测点处加速度时程频谱见图7。可知，地铁列车经过时地表振动加速度主要频率为35～60 Hz。

图7 测点处加速度频谱

3.2 最优方案

通过现场实测获得弹性波在土层中传播的频率主要集中在35～60 Hz，结合带隙影响因素规律的研究，考虑方案的可行性，采用以下方案进行设计：正方形布置排桩，周期常数3 m，桩半径采用1 m，材料参数同表1一致。

4 周期性排桩隔振性能效果分析

将周期性排桩布置在长度为52.5 m，宽度为18 m的矩形波导中，如图8所示。使用最优方案设计参数，在矩形上下边设置无限周期性边界条件，水平向设置不同排数的排桩。弹性波从矩形波导的左侧边界入射，扫频范围为1～100 Hz，加速度幅值为1 m/s2，频率响应函数曲线方程为

FRF=20lg(ai/a0)

(4)

式中：FRF为频率响应函数，dB;ai为右侧边界处加速度响应幅值;a0为左侧边界加速度激励荷载的幅值。

图8 三排桩矩形波导布置

图9给出了周期性排桩排数b分别采用1,3,5,7时模型中的加速度频率响应函数。可知：隔振排桩的带隙频率主要集中在50～60 Hz，且随着排桩排数的增加隔振性能逐渐增加且带隙宽度逐渐增加。

图9 不同桩排数下的加速度频率响应

排桩采用7排布置时，矩形波导区域内衰减幅度云图见图10。由图10(a)可知：在矩形波导的右侧边界衰减幅度在50 dB左右，从衰减域云图的变化规律可以看出，弹性波经过第3个周期后其幅值大幅度减小。由图10(b)可知：当弹性波的频率在衰减域范围之外时，弹性波可顺利穿过排桩向前传播，排桩对该频率下的弹性波没有起到隔振作用。

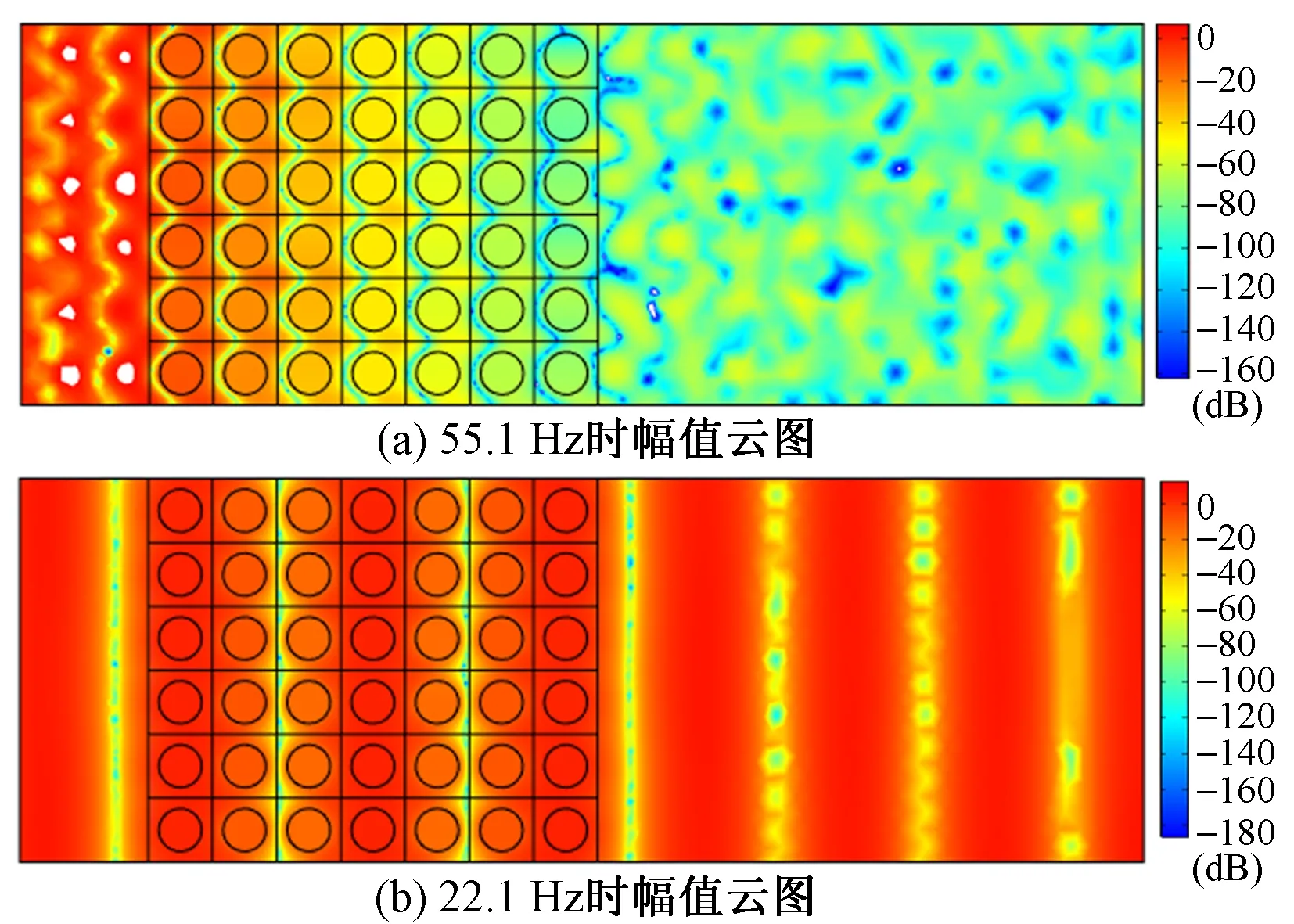
图10 布置7排桩矩形波导区域内衰减幅值云图

5 结论

本文基于声子晶体带隙理论研究周期性隔振排桩带隙变化规律，针对城市轨道交通运营引起近场土体的振动特性，设计出对应隔振频段的排桩布置参数，并计算其减振效果，得出如下结论：

1)通过现场实测，城市轨道交通在普通道床轨道形式下运行引起的近场土体振动特征频率为35～60 Hz。

2)周期性排桩带隙频率与城市轨道交通引起近场土体振动频率相近，可通过调整排桩参数设计出适合不同条件下土体中弹性波的特征频率的周期性排桩形式。

3)混凝土桩体的材料属性参数、周期常数和土体的材料属性参数对周期性排桩的带隙有明显的影响。可通过合理选取参数对周期性排桩进行带隙设计。

4)通过加速度传递函数分析对周期性排桩带隙进行验证，表明隔振排桩对城市轨道交通运营引起近场土体振动特征频带具有良好的减振效果。

[1]夏禾.交通环境振动工程[M].北京:科学出版社,2010.

[2]KUSHWAHA M S,HALEVI P,MARTINEZ G,et al.Theory of Acoustic Band-structure of Periodic Elastic Composites[J].Physical Review B Condens Matter,1994,49(4):2313-2322.

[4]温熙森,温激鸿,郁殿龙,等.声子晶体[M].北京:国防工业出版社,2009.

[5]温激鸿,王刚,郁殿龙，等.声子晶体振动带隙及减振特性研究[J].中国科学(E辑:技术科学),2007,37(9):1126-1139.

[6]陈慧珉,常红,李建宝.材料参数对二维正交异性声子晶体带隙的影响[J].太原科技大学学报,2013,34(5):378-387.

[7]卢天健,高国钦,马守林，等.二维四方排列半圆铝管/空气声子晶体的禁带特性[J].中国科学(E辑:技术科学),2009,39(1):57-64.

[8]沈惠杰,李雁飞,苏永生,等.舰船管路系统声振控制技术评述与声子晶体减振降噪应用探索[J].振动与冲击,2017,36(15):163-70,209.

[9]于坤鹏,王志海.基于声子晶体的二维减振结构设计[J].机械与电子,2016(2):12-15.

[10]刘宗发,吴斌,何存富.最优二维固/固声子晶体带隙特性研究[J].固体力学学报,2015,36(4):283-289.

[11]黄建坤.周期性排桩和波屏障在土木工程减振中的应用研究[D].北京:北京交通大学，2014.

[12]李建宝,汪越胜,张传增.二维声子晶体微腔能带结构的有限元分析与设计[J].人工晶体学报，2010,39(3):649-55，64.

[13]LIU X N,HU G K,SUN C T,et al.Wave Propagation Characterization and Design of Two-dimensional Elastic Chiral Metacomposite[J].Journal of Sound and Vibration,2011,330(11):2536-2553.