高性能混凝土碳化深度的灰色系统理论计算模型
2018-06-04王建华
陈 萌,王建华,苗 丽
(1.郑州大学 土木工程学院,河南 郑州 450002;2.河南省建筑科学研究院有限公司,河南 郑州 450053;3.郑州大学 水利与环境学院,河南 郑州 450002)
工程中混凝土碳化深度的计算,由于影响因素和不确定性因素众多,只能是一个追求高精确率的估算过程。碳化深度作为一个随机变量,数据样本少,且跨越较长的龄期,有的可达几年甚至几十年,因此,对碳化深度进行较为准确的估算,颇具工程意义。国内外学者自20世纪开始,对碳化深度的估算进行了深入系统的研究,已建立的预测公式大致分为基于扩散理论建立的理论公式和基于混凝土碳化试验建立的经验公式2大类。理论公式中有些变量不易在工程中实际测得,而经验公式的数据样本少,不能完全体现混凝土碳化深度的变化规律,二者均存在一定的不足和局限性。
上述的成果都是以普通混凝土为研究对象而得出的,作为绿色建材之一的高性能混凝土,其组分和性能较以往的普通混凝土有了明显的变化和改善,它的碳化深度变化规律不同于普通混凝土的变化规律。高性能混凝土以高耐久性、实现全过程控制和提高建筑产品质量等优点,自2013年起,开始在房屋建筑工程和铁道工程中推广应用。由于高性能混凝土在工程中应用的时间较短,它的碳化深度数据序列呈现小样本、贫信息、不确定性等基本特性。
20世纪80年代由中国学者创立并完善的灰色系统理论,着重解决模糊数学、概率统计所难以解决的小样本、贫信息、不确定性等问题,其特点是“少数据”建模,通过对已知的“少数据”的生成和开发,提取有价值的信息,探索数据序列的发展变化规律。
本文将灰色系统理论应用于高性能混凝土碳化深度的模拟和预测中,结合项目组持续进行的高性能混凝土碳化深度试验结果,对8个高性能混凝土构件的碳化深度进行灰色建模,并依据灰色模型模拟计算的误差变化规律,给出建立高性能混凝土碳化深度灰色系统理论计算模型的基本方法[1-3]。
1 高性能混凝土的碳化深度试验
自2001年3月,对8个高性能混凝土构件持续进行了碳化深度的测量,测量方法依据JGJ/T 23—2011《回弹法检测混凝土抗压强度技术规程》[4]。8个高性能混凝土构件的尺寸(长×宽×高)均为 1 500 mm×600 mm×1 200 mm。碳化深度的测试龄期分别取为14,28,60,90,740 d和14年,测试环境为郑州地区室外环境。高性能混凝土28 d立方体抗压强度标准值的变化范围为42.1~76.4 MPa。高性能混凝土的6种组分分别为:P.O 42.5和P.O 52.5水泥;中砂;粒径5~20 mm碎石;水;FN-2,FYH2,FDN减水剂和UEA膨胀剂;粉煤灰和硅粉掺合料。高性能混凝土的配合比见表1[5]。
2 灰色系统理论计算模型的建立
灰色系统理论的GM(1,1)模型适用于具有明显指数规律且为等间隔的数据序列计算,对于非等间隔数据序列,首先得将其转化为等间隔数据序列;其次,依据GM(1,1)模型模拟计算的误差变化规律,通过优化序列边界和序列参数,保证GM(1,1)模型的模拟数据序列和原始数据序列的最佳拟合。
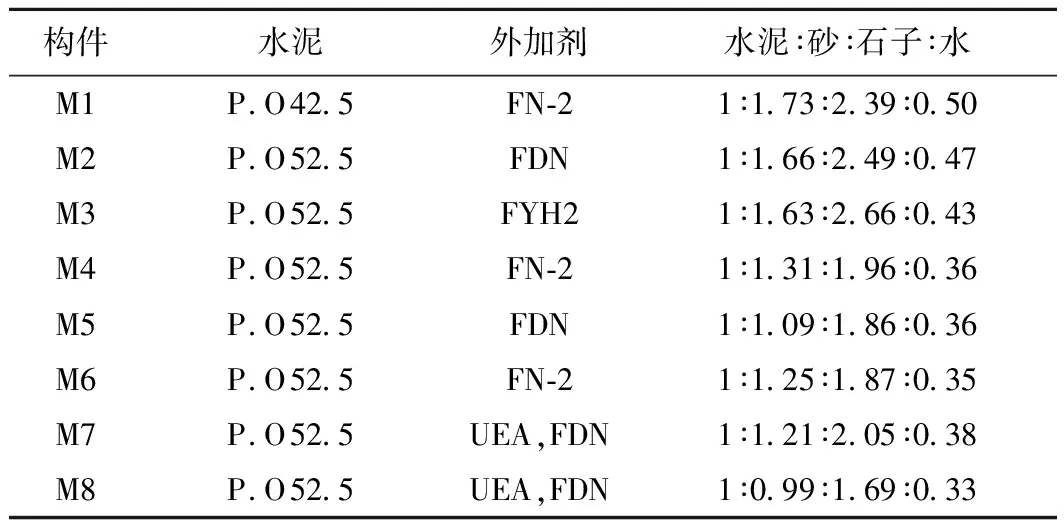
表1 高性能混凝土的配合比
注: UEA为膨胀剂;FN-2,FYH2和FDN分别为不同的减水剂。
2.1 非等间隔GM(1,1)模型的转换和计算
非等间隔数据序列转换为等间隔数据序列的计算方法如下[6-8]。
设非等间隔序列Y(0)为
Y(0)=[y(0)(t1),y(0)(t2),…,y(0)(tn)]
(1)
式中:n为有限个测量数据的总数量;tn为第n个测量数据对应的时间。
计算非等间隔序列的平均时间间隔Δt0为
(2)
式中:k为实际测量数据的数量;tk为实际测量数据的最终时间;t1为实际测量数据的初始时间;Δti为各段时间间隔,Δti=ti+1-ti,i=1,2,…,k-1。
时间间隔差系数δ(tk)为
(3)
则Y(0)序列总差值Δy(0)(tk)的计算公式为
Δy(0)(tk)=δ(tk)[y(0)(tk+1)-y(0)(tk)]
(4)
由非等间隔序列Y(0)转换而来的等间隔序列X(0)为
X(0)=[x(0)(t1),x(0)(t2),…,x(0)(tn)]
(5)
其中
x(0)(tk)=y(0)(tk)-Δy(0)(tk)
(6)
然后对转换而来的等间隔序列X(0)按GM(1,1)模型进行模拟计算。
生成等间隔序列X(0)的一次累减序列X(1)为
X(1)=[x(1)(t1),x(1)(t2),…,x(1)(tn)]
(7)
其中
x(1)(tk)=x(0)(tk)-x(0)(tk-1),k=2,…,n
(8)
X(1)的紧邻均值生成序列Z(1)为
Z(1)=[z(1)(t2),z(1)(t3),…,z(1)(tn)]
(9)
其中
z(1)(tk)=0.5[x(1)(tk)+x(1)(tk-1)],k=2,…,n
(10)

(11)
GM(1,1)模型x(0)(tk)+az(1)(tk)=b的最小二乘估计参数列为
(12)
(13)
式中:x(0)(t1)为转换而来的等间隔序列X(0)的初始值;-a为发展系数,表示X(0)的发展态势;b为灰色作用量,是从已知数据中挖掘出来的数据,表示数据变化规律。
根据吸附-解吸等温线Freundlich方程拟合的吸附常数值计算9个地区供试土样对Cd的解吸滞后系数(HI)。由表3可知,1号、4号和8号土样的HI>1,说明存在负迟滞现象,而2号、3号、5号、6号、7号和9号土样的HI<1,说明存在正迟滞现象,可能是不同土壤间理化性质差异引起,土壤中的解吸迟滞效应可能导致Cd在土壤中短暂积累,从而对土壤造成污染,继而通过食物链富集到人体内,危害身体健康。
(14)
2.2 优化序列边界
在采用灰色系统理论对等间距序列建模的过程中,原始序列的数据不一定全部用来建模[9]。
对于等间隔原始序列X(0),用X(0)中的所有数据x(0)(t1),x(0)(t2),…,x(0)(tn)建立的GM(1,1)模型即为全数据模型;删除掉最老信息x(0)(t1),增加最新信息x(0)(tn+1),用X(0)=[x(0)(t2),x(0)(t3),…,x(0)(tn+1)]建立的GM(1,1)模型即为新陈代谢模型。
由参考文献[10]中计算实例的计算精度比较可以看出,新陈代谢模型的模拟精度比全数据模型的模拟精度高且预测效果好。这是因为数据序列也是不断发展变化的,随着时间的发展,老数据已不能反映数据序列的发展规律;尤其是数据变化由量变的积累发展到质变的飞跃时,现在和将来的序列已明显不同于过去的序列,此时,再采用全数据模型建模,已不能反映数据的特征规律,而应选取新陈代谢模型,逐次删除老数据,随时将每个新数据加入到X(0)中,逐次以x(0)(tk)(k=2,3,…)为初始数据进行GM(1,1)模型计算。
2.3 优化序列参数
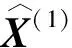
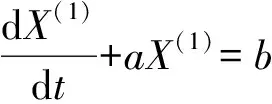
(15)
式中,α和β为常数。
采用最小二乘法求出α和β的估计值。
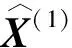
(16)
分别求出Z对α和β的一阶偏导数,令一阶偏导数等于0,即:
(17)
(18)
求解式(17)和式(18),得
(19)
(20)
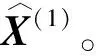
3 高性能混凝土碳化深度的灰色模型计算结果
8个构件的碳化深度实测数据分别对应于14,28,60,90,740 d和14年的龄期,属于非等间隔数据序列。按照2.1节中的方法将非等间隔数据序列转换为等间隔数据序列,表2中给出了M6构件的非等间隔数据序列的转换过程。
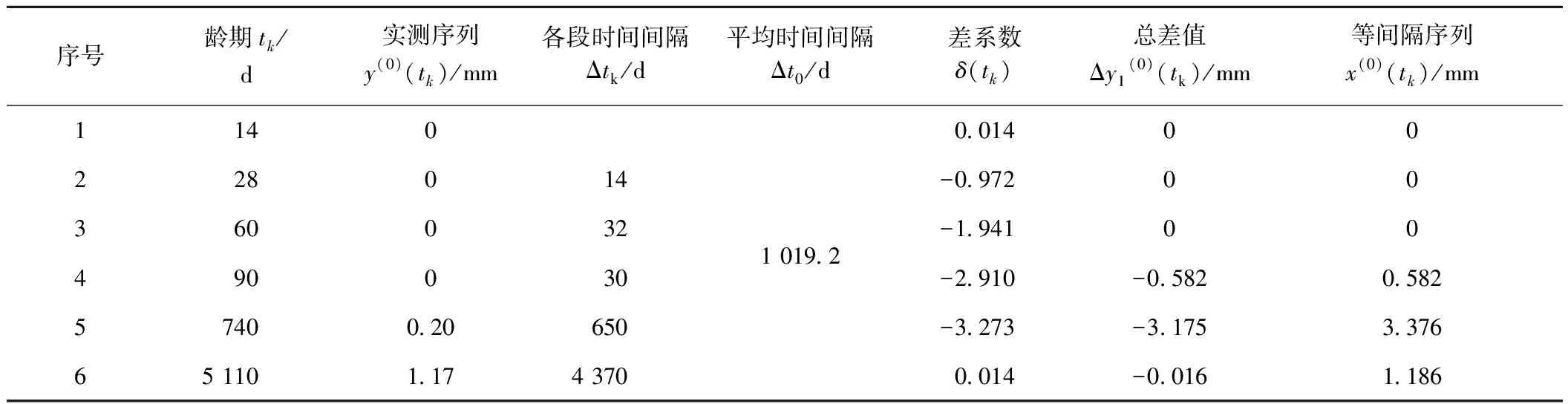
表2 M6构件非等间隔数据序列转换为等间隔数据序列的计算过程
表3为试验构件碳化深度实测数据与模拟数据的计算结果与误差检验。由表3中8个构件碳化深度的实测结果可以看出,随着龄期的增加,每个构件的碳化深度数据符合或大致符合指数发展规律,因此,可以选用GM(1,1)模型对8个构件的碳化深度进行模拟计算。
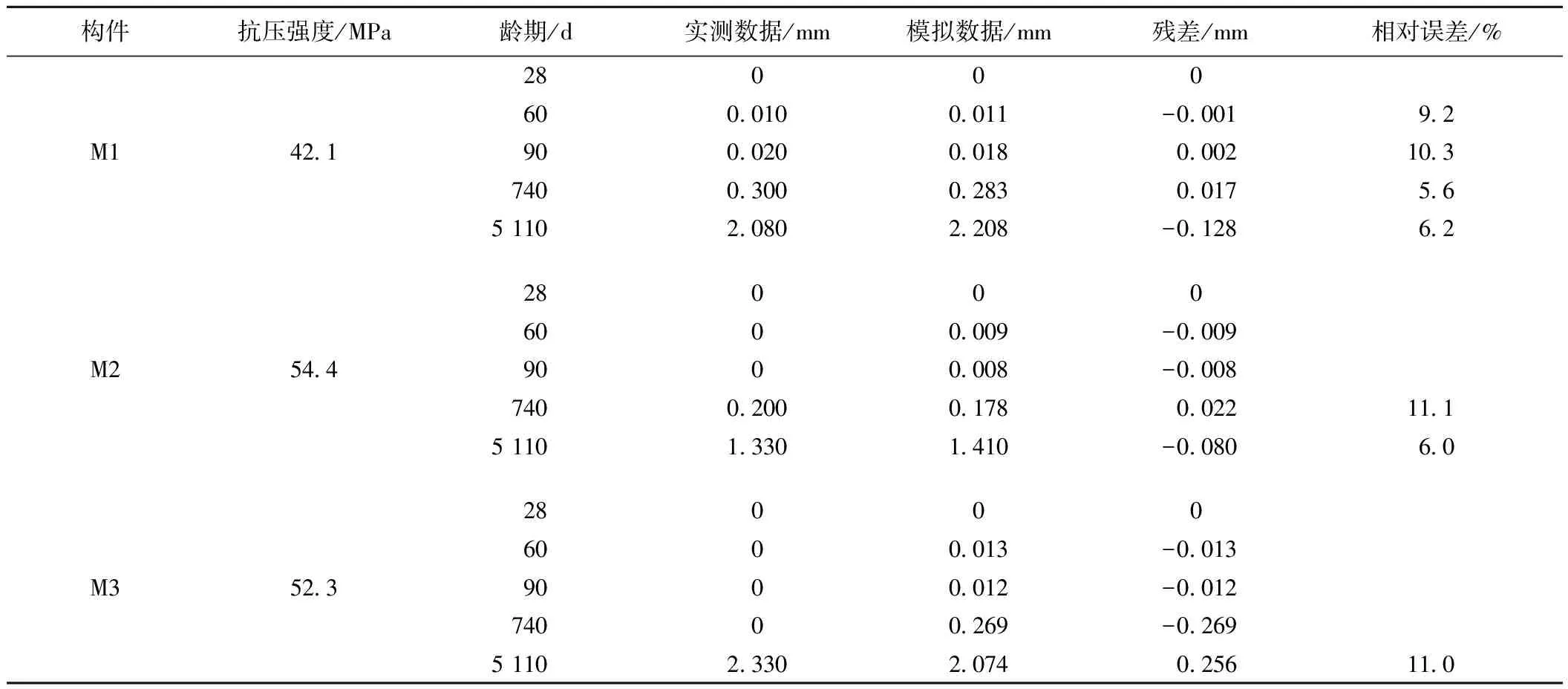
表3 试验构件碳化深度实测数据与模拟数据的计算结果与误差检验
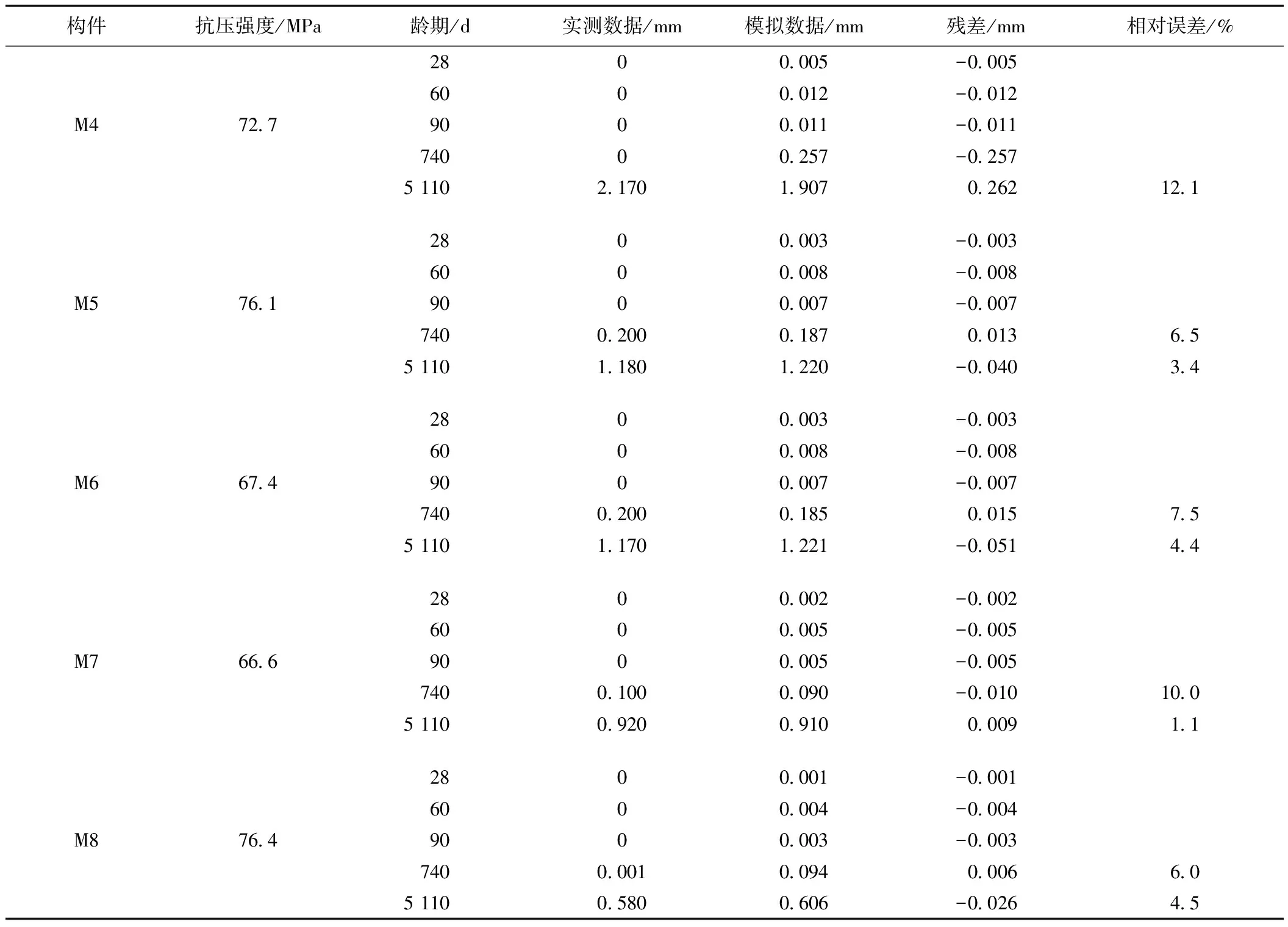
续表3
注:残差为实测数据与模拟数据的差值;相对误差为实测数据与模拟数据差值的绝对值除以实测数据。
为提高碳化深度的模拟精度,采用2.2节的优化序列边界方法和2.3节的优化序列参数方法进行计算。采用新陈代谢模型,删除掉8个构件的14 d碳化深度数据,增加最新的14年碳化深度数据,以28 d碳化深度数据作为初始数据进行GM(1,1)模型的模拟计算;优化序列边界之后,采用最小二乘法优化白化方程中通解的参数,以保证GM(1,1)模型模拟序列和实测序列的最佳拟合。由表3可知,8个构件不同龄期的实测结果与模拟结果的相对误差变化范围为1.1%~12.1%,计算精度满足要求,验证了灰色理论计算模型的正确性和可行性。
4 结论
1)对8个高性能混凝土实体构件持续进行了龄期为14,28,60,90,740 d和14年的碳化深度测量,构件混凝土的28 d立方体抗压强度为42.1~76.4 MPa;测试环境为郑州地区室外环境,8个构件14年的碳化深度为0.58~2.33 mm。
2)8个构件不同龄期的碳化深度符合或大致符合指数发展规律,采用灰色系统理论GM(1,1)模型进行建模计算;根据灰色模型模拟计算的误差变化规律,给出非等间隔数据序列的转换、优化数据序列边界和优化数据序列参数等建模基本方法;8个构件碳化深度的灰色理论模拟数据与实测数据符合良好,验证了灰色系统理论计算模型的正确性和可行性。
3)为计算简便,应首先选用优化数据序列边界的方法,当模拟精度不满足要求时,再进行优化数据序列参数的方法。
[1]孙炳全,刘国志,刘玉莲.混凝土碳化灰色预测模型研究[J].建筑材料学报,2012,15(1):42-47.
[2]MONTEIRO I,BRANCO F A,de BRITO J,et al.Statistical Analysis of the Carbonation Coefficient in Open Air Concrete Structures[J].Construction and Building Materials,2012,29(4):263-269.
[3] CHENG F C,JING W C.The Experimental Investigation of Concrete Carbonation Depth[J].Cement and Concrete Research,2006,36(9):1760-1767.
[4]中华人民共和国住房和城乡建设部.JGJ/T 23—2011 回弹性检测混凝土抗压强度技术规程[S].北京:中国建筑工业出版社,2011.
[5]刘乐庆.长龄期高性能混凝土碳化深度的试验研究[D].郑州:郑州大学,2017.
[6]罗佑新.非等间距新息GM(1,1)的逐步优化模型及其应用[J].系统工程理论与实践,2010,30(12):2255-2258.
[7]罗佑新.数据处理的等间距化GM(1,1)模型与方法[J].机床与液压,2005(6):148-149.
[8]李福琴.灰色模型的稳定性和建模精度研究[D].武汉:武汉理工大学,2006.
[9]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990.
[10] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010.
[11]汪荣鑫.数理统计[M].西安:西安交通大学出版社,1996.
