基于超声导波的道岔尖轨伤损监测试验研究

付连著，伍建军，郎向伟，唐志峰

(1.中国铁道科学研究院 深圳研究设计院，广东 深圳 518055；2.浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027；3.浙江大学 数字技术与仪器研究所，浙江 杭州 310027)

道岔尖轨在服役过程中，由于受到材料特性、环境温度及轮轨之间复杂应力的影响，容易出现压溃、侧磨、波磨、剥离、裂纹等不同程度的伤损。在轮轨间相互作用引起的纵向及侧向动载荷的作用下，伤损扩展更加迅速，可能在没有征兆的情况下突然造成失效，情况严重时会造成尖轨损坏甚至断裂，产生列车脱轨等事故，造成人员伤亡和巨大的经济损失。由此可见，对于尖轨伤损的无损检测和监测至关重要。

现有的尖轨伤损离线检测方法包括使用轨距尺、直尺等基本测量工具进行人工检测和使用仪器进行检测。仪器检测包括超声检测[1-2]、漏磁检测[3-4]、涡流检测[5-6]、机器视觉检测[7]、射线检测[8]等。上述技术经过多年发展已经形成了比较完整的检测体系，并开发了一系列比较成熟的检测系统。这些轨道无损检测系统的特点是逐点扫描，可在天窗时间段进行伤损检测，但无法在铁路运行过程中进行实时监测。并且铁路现用机载或手持检测设备几乎全是针对基本轨开发的，探测的区域仅仅是轨面宽度>50 mm的部位，尖轨细端向内有3 m左右是检测盲区。除此之外，由于轨底有扣件扣压和润滑油污的覆盖，钢轨底面边缘区域是传统超声检测车的检测盲区。因此，对于工作状态下的道岔尖轨伤损，尚无行之有效的离线检测或者在线监测的方法。

超声导波检测技术具有长距离、大范围、全截面、便捷性、特征参量丰富等其他方法难以媲美的优势，可弥补上述检测技术的不足，已成为无损检测领域蕴含巨大发展潜力的方法之一，并成为相关研究的热点[9-10]。因此，开展超声导波尖轨伤损在线监测研究具有十分重要的理论意义和实用价值。

本文在分析道岔尖轨中超声导波传播特性的基础上，通过理论分析、有限元仿真和监测试验，验证利用超声导波监测道岔尖轨伤损的可行性，为未来智能铁路的在线无损监测技术进行有益探索。

1 尖轨导波模态分析

尖轨是一个变截面波导，但是尖轨轨头部分是行车区段，无法安装换能器实现导波的激励与接收。轨腰和轨底区域沿着尖轨轴向的截面变化程度不大，可以近似看作非变截面波导。对于截面不规则的非变截面波导，半解析有限元法是合适的。导波在不规则的非变截面波导中的传播过程是一个弹性波的传播过程。半解析有限元法认为其沿着波传播方向为简谐振动，仅需离散求解截面的波动方程即可。截面的波动方程可通过哈密顿方程结合动势能推导，即

(1)

式中：Φ为应变能;K为动能。其具体表达式为

(2)

(3)

把式(2)和式(3)代入式(1)可得

(4)

假设波传播方向为x轴方向，则截面为y-z平面。将波导的截面区域离散后，其任意节点e的位移u(e)为

(5)

式中:k为波数;ω为角频率;N为形状函数矩阵，具体依节点网格形式而定。

(6)

式中，Uαβ(α=x,y,z;β=1,2,3)表示节点β在α方向上的位移。

则节点e相应的应变矢量ε(e)可由下式计算求得：

(7)

其中

(8)

节点e相应的应力矢量σ(e)可由下式计算求得：

σ(e)=C(e)ε(e)

(9)

式中，C(e)是全局坐标下单元的材料刚度矩阵。

把式(5)代入式(7)可得

ε(e)=(B1+ikB2)Q(e)ei(kx-ωt)

(10)

其中

B1=LyN,y+LzN,z,B2=LxN

(11)

式中：N,y和N,z为y和z向的形状函数矩阵。

把式(5)、式(10)代入式(4)中，所得的方程可对每个单位元进行数值计算。对所有的单位元用传统的有限元装配方法进行装配，即可得到全局坐标系下的特征值方程

(12)

其中

(13)

式(12)可被进一步改写成一个一阶特征系统

[A-kB]Q=0

(14)

其中

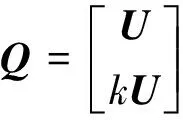
(15)

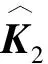
代入不同的波数k求解式(14)即可获得频散曲线以及不同模态相应的波结构。

选择60AT尖轨进行建模，其材料密度为 7 850 kg/m3，弹性模量为210 GPa，泊松比为0.33。求得的频散曲线如图1所示。可以看出，随着频率的增加，同一频率下模态数量增加，每一种模态随着频率变化其速度都在变化，也就是存在频散的特征。高频造成多模态，会导致检测信号更为复杂，提高信号分析难度；低频会导致检测灵敏度降低。综合考虑，设定检测频率为60 kHz。在该频率下，以轨底窄边和轨腰为例，其合适的导波模态如图2所示。

图1 尖轨导波频散曲线

图2 60 kHz导波模态

2 基于超声导波的尖轨有限元仿真

2.1 尖轨简化模型

根据60AT尖轨的实际尺寸建立三维有限元模型，长度设定为2 m。设定的材料属性如上节。尖轨未建立变截面模型，因为在轨腰和轨底区域尖轨横截面变化不大，可以以非变截面模型作为仿真基础。如上所述，根据频散曲线选定激励频率为60 kHz。激励信号为5周期汉宁窗调制的正弦信号，设置在模型的一端进行激励。

激励与接收设置如图3所示，在激励的同一位置设计接收点。缺陷设置如图4所示，轨底窄边的槽形缺陷深度为7.4 mm，轨腰缺陷深度为10 mm。激励点位于模型中间位置，缺陷距离激励点0.5 m。

图3 激励与接收设置

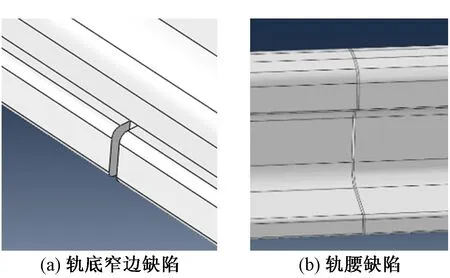
图4 缺陷设置

图5 导波传播过程

2.2 仿真分析

图5为尖轨轨底窄边和轨腰位置的导波传播过程。可以看出，导波从模型中间开始激励，轨底窄边的波包在传播过程中保持良好的完整性，未发生明显扩散；轨腰位置的波包相对来说完整性要差一些；2个位置的导波在传播过程中碰到缺陷后都会有明显的回波。从图6所示的监测信号中可以看出，缺陷回波位于始波和端面回波中间，符合仿真设置；轨底窄边的监测信号信噪比相对于轨腰位置更高。

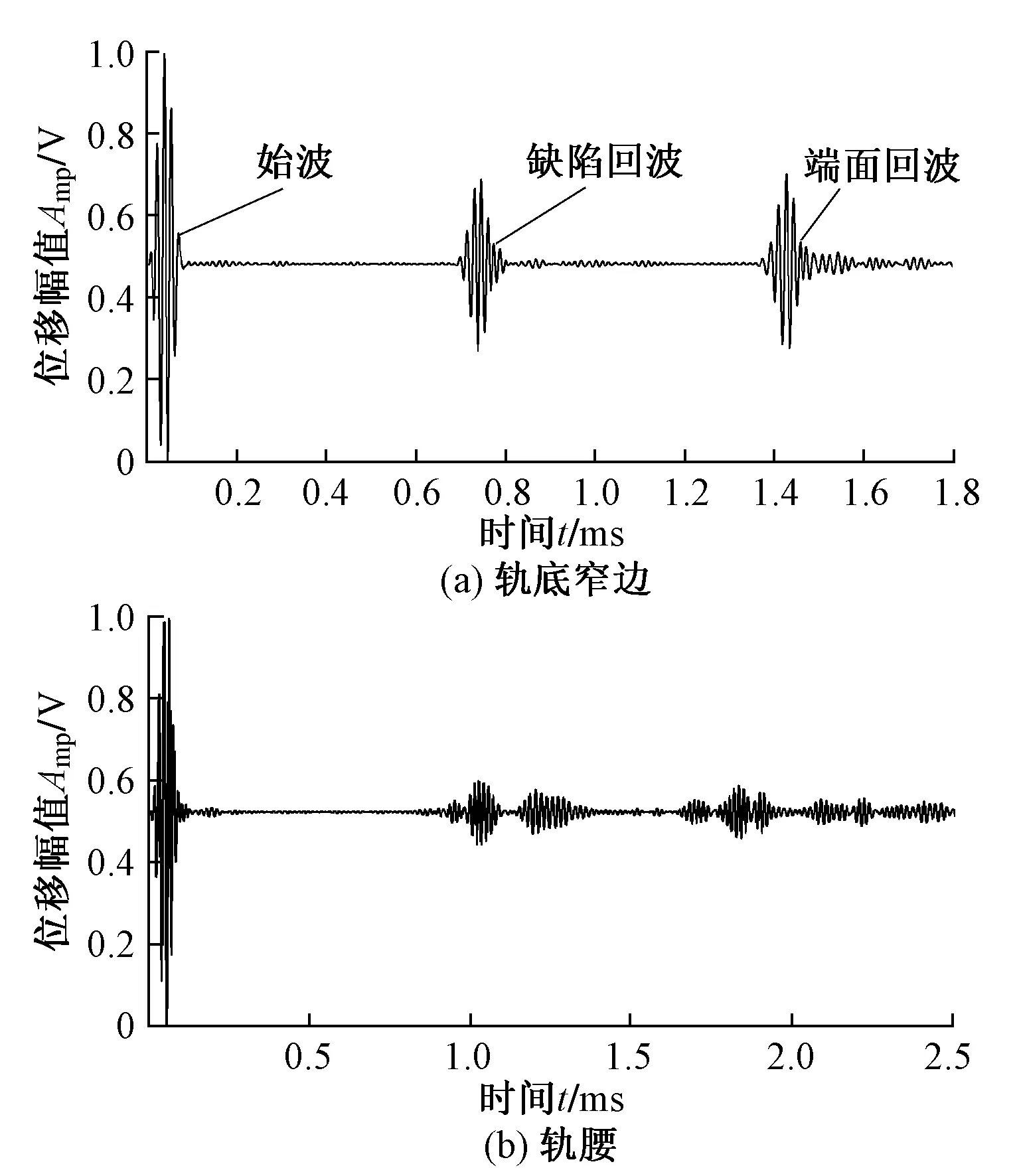
图6 监测信号

3 基于超声导波的尖轨现场监测试验

3.1 试验装置

仿真分析验证了超声导波检测尖轨轨底和轨腰位置缺陷的可行性。但是在现实环境中存在的环境噪声会严重降低检测信号的信噪比，使得检测信号中的信息无法辨识。因此采用监测的方式来对比当前检测信号和无伤损状态下的检测信号以做出判别，是一种较为理想的方式。

图7 监测试验示意

图7为监测试验示意。监测试验对象为1根长度为4.58 m的尖轨，换能器安装在距离尾端0.94 m处。轨底窄边存在一定的截面变化，在轨腰位置换能器前后都有不同尺寸的通孔，轨头存在着严重的截面变化。监测试验仅在尖轨轨腰和轨底窄边区域进行。选择了2个位置来耦合质量块用以模拟缺陷，第1个位置在四连孔和换能器之间，距离换能器1.5 m处，第2个位置在四连孔和尖端之间，距离换能器2.5 m。使用的换能器为压电式换能器。因单个换能器无法实现导波声场的方向控制，因此检测信号中只能分辨特征波包所代表的特征与换能器之间的距离，无法得知其方向。

本文中采取的信号处理方法为基于独立成分分析的结构健康监测算法[11-12]。该算法的基本原理为将信号基于独立性进行分解。对应于某一些独立分量，这些独立分量在基准信号和当前测量信号中所占的权重不同，在权重矢量中形成阶跃特征;而如果当前测量情况下无缺陷等突变因素的存在，那么信号经过ICA(Independent Component Analysis)分解后，独立分量对应的权重矢量不会存在阶跃特征。因此根据阶跃特征可判别是否有缺陷出现，根据独立分量获得监测信号可确定缺陷变化的位置。

3.2 试验分析

在轨底窄边距离换能器1.5 m处耦合了截面尺寸为10 mm×30 mm的小铁块，用以模拟缺陷，所占的截面损失为3.40%。检测所得轨底窄边耦合小铁块前后的典型原始信号如图8所示。仅从原始信号中无法直接区分出模拟缺陷的特征波包。经过信号处理后可从图8中分离出2组存在阶跃特征的权重矢量及其独立分量，如图9(a)所示。这说明耦合小铁块前后的信号存在差异。从图9(b)的监测信号中可以看出，信号差异突变的特征首先发生在约1.5 m处,这表明缺陷位置在1.5 m处，与实际情况相符。

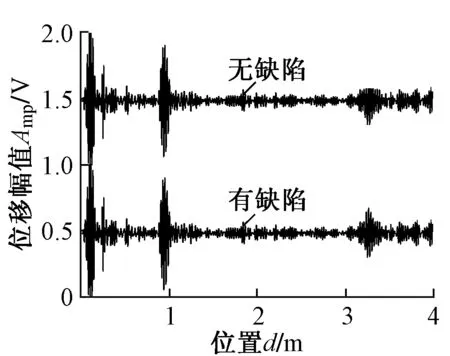
图8 轨底窄边原始检测信号对比

图9 轨底窄边监测分析结果

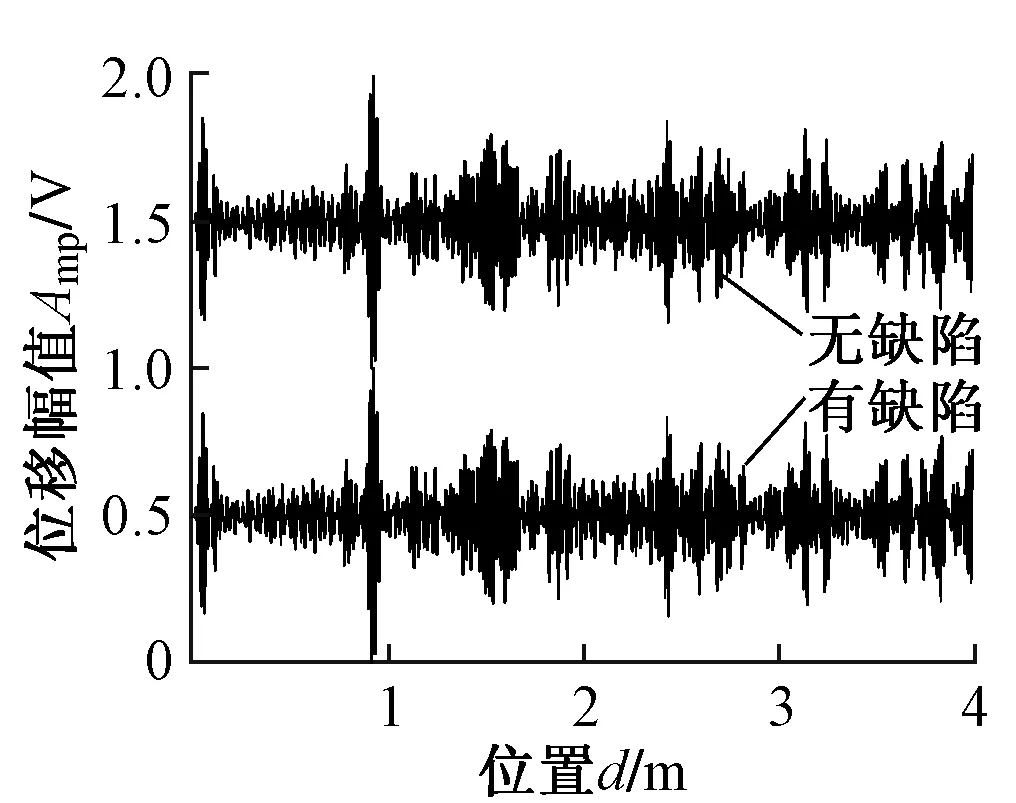
图10 轨腰原始检测信号对比

轨腰区域在距离换能器2.5 m处耦合了截面尺寸为20 mm×30 mm的小铁块，用以模拟缺陷。轨腰原始信号对比如图10所示。同样地，仅从原始信号中无法确认缺陷位置。经过独立成分分析处理后可找到数个独立分量的权重矢量是存在阶跃特征的，如11(a)所示。通过观察图11(b)的监测信号可确定缺陷的位置在2.5 m处，与试验设置相符。

图11 轨腰监测分析结果

4 结论

1)仿真分析和试验证明，60 kHz的超声导波是道岔尖轨伤损检测与监测较为合适的激发频率。

2)试验结果表明，通过监测手段，采用60 kHz的超声导波能够监测到超过3.40%截面变化的缺陷。

3)基于超声导波的尖轨伤损监测技术能够排除尖轨中存在的固有特征的影响，提取出缺陷引起的信号变化，相对于超声导波检测具有更高的灵敏度。

4)在下一阶段的研究中，将对实际工作的道岔尖轨进行监测试验，以验证超声导波监测技术的监测效果。实际工作中的尖轨所处环境更为复杂，需要对监测系统包括监测仪器、导波换能器、信号传输模块以及监测算法等各环节进行进一步优化，以提高采集信号的稳定性和信噪比，达到良好的监测效果。

[1]张玉华,许贵阳,李培,等.钢轨探伤车自主化超声检测系统的关键技术[J].中国铁道科学,2015,36(5):131-136.

[2]许霁,邱玉,汪开灿,等.钢轨踏面电磁超声检测信号处理方法[J].无损检测,2012,34(5):33-36.

[3]熊龙辉.钢轨裂纹漏磁检测技术研究[D].南京：南京航空航天大学,2014.

[4]贾晓媛.基于漏磁原理的钢轨裂纹高速检测[D].南京：南京航空航天大学,2012.

[5]李国厚,黄平捷,陈佩华,等.涡流检测在钢轨裂纹定量化评估中的应用[J].浙江大学学报(工学版),2011,45(11):2038-2042，2049.

[6]丁勤.国外钢轨涡流检测技术现状[J].钢铁钒钛,1996(4):58-62.

[7]谭松,李唯一,韩强.基于计算机视觉的车载钢轨光带异常检测系统研制[J].铁道建筑,2016,56(2):128-131.

[8]邬冠华,熊鸿建.中国射线检测技术现状及研究进展[J].仪器仪表学报,2016,37(8):1683-1695.

[9]周建民,徐清瑶,李鹏,等.钢轨无损检测中的超声导波技术[J].仪表技术与传感器,2015(6):99-102，106.

[10]严钦男.基于嵌入式的钢轨超声导波无损检测系统[J].湖北科技学院学报,2013,33(9):4-6.

[11]DOBSON J,CAWLEY P.Independent Component Analysis for Improved Defect Detection in Guided Wave Monitoring[J].Proceedings of the IEEE,2016,104(8):1620-1631.

[12]HUANG D S,MI J X.A New Constrained Independent Component Analysis Method[J].IEEE Transactions on Neural Networks,2007,18(5):1532-1535.