一类非线性耦合抛物型方程组解的整体不存在性
2018-06-04裴金仙
裴金仙
(山西大学商务学院 理学系, 山西 太原 030031)
本文研究如下非线性耦合抛物型方程的初边值问题
(1)
式中:Ω是Rn中具有光滑边界Γ=∂Ω的有界区域,d1>0,d2>0,p≥2,q≥2是常数,f1,f2,g1,g2为已知函数.
许多物理、力学、生物学和化学等问题可以用抛物型方程和方程组来表示, 关于相关系统解的整体存在性和解的爆破问题的研究具有非常重要的理论和实际意义, 也得到了很多结果[1-9].
ut-div(|u|p-2u)=uq,
(2)
方程(2)的初边值问题的研究已经有很多结果. 主要的结果是 (i)若q
ut-div((d+|u|p-2)u)+g(u,v)=f(u),
(3)
有许多关于解的爆破的结果. Erdem[10]研究了当d>0,p≥2以及f和g满足一定的条件时, 系统解的整体不存在性.
对于耦合的半线性抛物型方程组解的爆破也有一些结果. Wang M[11]研究了带有Dirichlet边界条件的方程组
ut=△u+uαvp,vt=△v+uqvβ,
(4)
式中:α,β,p,q是非负常数,α+p>0,β+q>0, 分别得到了解的整体存在性和解在有限时刻爆破的结果. Escobedo和Herrero[12]研究了式(4)的Cauchy问题, 找到了解整体存在和爆破的临界指数. Rossi和Souplet[13]研究了方程
ut=△u+um+vp,vt=△v+uq+vn
(5)
的初边值问题,m,n,p,q>1, 证明了当m>q+1,n>p+1时, 解(u,v)在有限时刻爆破. Li[14]研究了
ut-div(|u|p-2)u)=avα,
vt-div(|v|q-2)v)=buβ,
(6)
的初边值问题, 分别得到了解的整体存在性和解的爆破. Wang J[15]研究了
ut-div(|um|p-2)
vt-div(|vn|q-2)
(7)
分别得到了解的整体存在性和解的爆破. Ding[9]研究了
ut=div(D(u)u)-S(u)φ(v)),
vt=Δv-v+u,
(8)
式中:D,S,φ是满足一定条件的已知函数, 得到了系统的解的整体有界性.
本文研究耦合抛物型方程的初边值问题(1), 构造合适的泛函, 得到解的有限时刻爆破的结果, 并且给出了解爆破时刻的估计.
假设存在函数F(ξ,η), 使得
(ξ,η)∈R2.
记‖·‖表示通常的L2(Ω)范数‖·‖L2(Ω), 记‖·‖p表示通常的Lp(Ω)范数‖·‖Lp(Ω). 定义系统(1)的能量
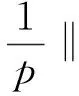
(9)
通过计算有

(10)
1 爆破结果
ξf1(ξ,η)+ηf2(ξ,η)≥2(γ+1)F(ξ,η),
(ξ,η)∈R2.
(11)
假设存在正常数τ1和τ2, 使得函数g1和g2满足
|gi(ξ,η,ζ,σ)|≤τi(|ξ|+|η|+|ζ|+|σ|),
(ξ,η,ζ,σ)∈R×R×Rn×Rn.
(12)
下面给出本文的主要结果.


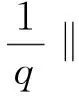
则系统(1)的解(u,v)在有限时刻t1爆破,
‖u‖2+‖v‖2→+∞,t→t1-0,
且爆破时刻的上界估计为
式中:β*和β为与初值无关的正常数.
证明构造合适的泛函H(t)满足微分不等式
H″(t)H(t)-(1+β)[H′(t)]2≥0,=
(13)
以及
H(0)>0,H′(0)>0.
(14)
利用文献[16]中引理1, 可以得到H(t)的有限时刻爆破, 进而得到定理1的结果.
首先作变换
φ(x,t)∶=e-λ tu(x,t),ψ(x,t)∶=e-λ tv(x,t),
其中, 常数λ>0待定. 经过计算式(1)变形为关于(φ,ψ) 的系统,
(15)
用φt乘以式(15)的第一个方程, 用ψt乘以式(15)的第二个方程, 将两式相加并在区域Ω上积分, 利用分部积分法得到


(16)
定义
(17)
由
(18)
和假设(11), 可得

(18)
结合式(18)和(19)可得
(20)
将式(20)代入式(16)得到如下估计

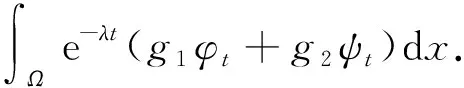
在全年下滑的态势中,新能源车成为仅有的亮点。据中国汽车工业协会发布数据显示,11月新能源汽车销量同比增长37.6%,1~11月同比增长68%。
(21)
令

则由式(21)和假设(12)得到估计


(22)
利用Young’s不等式和G(t)的定义, 可知存在正常数ε0<1/4使得

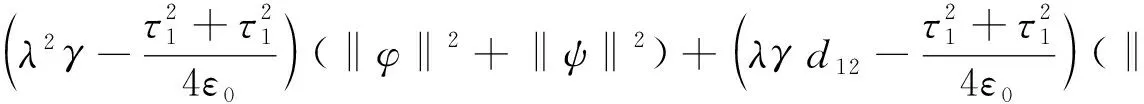
(1-4ε0)(‖φt‖2+‖ψt‖2)+2λγG(t),
(23)

(24)
用e-2λγt乘以式(23)的两边, 再在[0,t]上积分得到

‖ψs(x,s)‖2)ds.(25)
(25)
用φ乘以式(15)的第一个方程, 用ψ乘以式(15)的第二个方程, 将两式相加再在区域Ω上积分, 有
(d1‖φ‖2+d2‖ψ‖2)+eλt(p-2)‖
eλt(q-2)‖

(26)
由假设(12),G(t)的定义以及Young’s不等式可得
eλt(p-2)‖
ε1(‖φ‖2+‖
(γd1-ε1)‖φ‖2+(γd2-ε1)‖ψ‖2,
(27)
式中:ε1 结合式(25)和(27), 有如下估计 (28) 其中 (29) 从λ和ε0的选取可知 定义泛函 其中,β*是待定正常数. 通过计算有 H′(t)=‖φ‖2+‖ψ‖2. (30) 利用Hölder不等式可得 (31) 另一方面结合式(28)和(30), 有下面的估计 H″(t)≥4(γ+1)G(0)+4(γ+1)(1-4ε0)· 进一步对于合适的待定的β>0, 有 H″(t)H(t)-(1+β)[H′(t)]2≥4(γ+1)G(0)β*+ (32) 选取 则有 H″(t)H(t)-(1+β)[H′(t)]2≥0. 由于初值(u0,v0)满足 H′(0)=‖u0‖2+‖v0‖2>0, 和H(0)=β>0, 因此有H(t)的爆破, H(t)→+∞,t→t1-0, (33) 且 (34) 定理1得证. 参考文献: [1] Friedman A. Partial differential equations[M]. New York: Holt, Rinehart and Winston, Inc., 1969. [2] Jäger W, Luckhaus, S. On explosions of solutions to a system of partial differential equations modelling chemotaxis[J]. Trans. Amer. Math. Soc., 1992(329): 819-824. [3] Nagai T, Senba T. Global existence and blow-up of radial solutions to a parabolic-elliptic system of chemotaxis[J]. Adv. Math. Sci. Appl., 1998(8): 145-156. [4] Winkler M, Djie K. Boundedness and finite-time collapse in a chemotaxis system with volume-filling effect[J]. Nonlinear Anal., 2010(72): 1044-1064. [5] Winkler, M. Global solutions in a fully parabolic chemotaxis system with singular sensitivity[J]. Math. Methods Appl. Sci., 2011(34): 176-190. [6] Fujie K, Yokota T. Boundedness in a fully parabolic chemotaxis system with strongly singular sensitivity[J]. Appl. Math. Lett., 2014(38): 140-143. [7] Mi Y, Mu C. Global existence and blow-up of solutions to a class of doubly degenerate parabolic equations coupled via nonlinear boundary flux[J]. Adv. Math., 2014(43): 398-410. [8] Li G, Yu J, Liu W. Global existence, exponential decay and finite time blow-up of solutions for a class of semilinear pseudo-parabolic equations with conical degeneration[J]. J. Pseudo-Differ. Oper. Appl., 2017, 8(4): 629-660. [9] Ding M. Global boundedness in a fully parabolic quasilinear chemotaxis system with singular sensitivity[J]. J. Math. Anal. Appl., 2018(461): 1260-1270. [10] Erdem D. Blow-up of solutions to quasilinear parabolic equations (English summary)[J]. Appl. Math. Lett., 1999, 12(3): 65-69. [11] Wang M. Global existence and finite time blow up for a reaction-diffusion system[J]. Z. Angew. Math. Phys., 2000(51): 160-167. [12] Escobedo M, Herrero M. Boundedness and blow up for a semilinear reaction-diffusion system[J]. J. Diff. Equns. 1991, 89(1): 176-202. [13] Rossi J, Souplet P. Coexistence of simultaneous and nonsimultaneous blow-up in a semilinear parabolic system[J]. Diff. Integ. Equns., 2005(18): 405-418. [14] Li F. Global existence and blow-up solutions to a quasi-linear degenerate parabolic system[J]. Math. Acta Sci., 2008(28A): 1187-1193. [15] Wang J. Global existence and blow-up solutions for doubly degenerate parabolic system with nonlocal source[J]. J. Math. Anal. Appl., 2011(374): 1187-1193. [16] Kalantarov V, Ladyzenskaja O. The occurence of collapse for quasilinear equation of parabolic and hyperbolic types[J]. J. Sov. Math., V. 1978(10): 53-70.