HG AR—PNN在网络入侵检测中的应用

张宝华

Application of HG AR-PNN Classifier in Network Intrusion Detection

摘要：人工神经网络（ANN）大大提高了入侵检测系统的检测性能，但对于出现次数较少的攻击，ANN并不能提供令人满意的稳定性和检测率。提出了一种基于超图Helly性质和算术取余概率神经网络（HG AR-PNN）的入侵检测新方法。该方法利用超图的Helly性质选取最优特征子集，再对最优特征子集进行归一化算术取余，然后实现概率神经网络对数据集的训练。最后，使用KDDCUP99数据集进行实验，并对HG AR-PNN算法的性能进行评价。实验结果表明，对于不常出现的攻击，HG AR-PNN分类器同样有着较好的稳定性和较高的分类精度。

Abstract： The learning model which is based on artificial neural network （ANN） can greatly improve the performance of intrusion detection system， but to the less frequent attacks， the ANN can not provide stability and satisfactory detection rate. A new intrusion detection method based on hypergraph Helly property and arithmetic residue probability neural network （HG AR-PNN） is proposed. This method uses hypergraph Helly property to select the best feature subset， and then normalize the optimal feature subset with arithmetic residue， after that， uses the PNN for training the data set. Finally， experiments are carried out using KDDCUP '99 data set， and the performance of HG AR-PNN algorithm is evaluated. The experimental results show that HG AR-PNN classifier has better stability and higher classification accuracy for less frequent attacks.

关键词：入侵检测；分类器；概率神经网络；超图

Key words： intrusion detection；classifier；PNN；hypergraph

中图分类号：TN915.08 文献标识码：A 文章编号：1006-4311（2018）15-0248-05

0 引言

随着计算机网络应用技术的不断发展，网络安全漏洞也发生着巨大的变化。由于新漏洞的复杂性，传统的安全机制（如用户身份验证、加密等）已经无法阻止恶意用户对网络系统的入侵。在这种情况下，入侵检测系统就成为了网络安全系统中抵御入侵攻击和异常活动的第二道防线。入侵就是试图破坏计算机网络系统的保密性、完整性和可用性的行为，而入侵检测就是监测计算机系统或网络中发生的事件，分析它们是否有入侵的迹象。一般来说，IDS可分为误用入侵检测和异常入侵检测两种，误用入侵检测的性能取决于新的入侵模式的不断更新，而异常入侵检测取决于决策[1]。

由于网络数据流量的庞大，现有的入侵检测系统都以基于统计规则的专家系统和机器学习等为发展方向。在各种机器学习方法中，人工神经网络（ANN）能够成功地应用于IDS，并且能够获得较好的分类效果[2]。

现有基于人工神经网络的入侵检测系统的缺点主要有：①由于数据集的不平衡性，系统对不频繁发生的入侵行为检测率低。②神经网络在高维数据集中会产生局部极小值。为了克服这些问题，本文提出了基于超图和算术取余概率神经网络（HG AR-PNN）的新方法，该方法在增强了结构稳定性的同时，也提高了IDS的检测率。

1 相关工作

1.1 概率神经网络

概率神经网络（Probabilistic Neural Networks，PNN）是由D. F. Specht在1990年提出的。主要思想是用贝叶斯决策规则，即错误分类的期望风险最小，在多维输入空间内分离决策空间。它是一种基于统计原理的人工神经网络，它是以Parzen窗口函数为激活函数的一种前馈网络模型[3]。PNN吸收了径向基神经网络与经典的概率密度估计原理的优点，与传统的前馈神经网络相比，在模式分类方面尤其具有较为显著的优势。

由贝叶斯决策理论：

其中，xT是训练输入样本，x是未知分类的样本，σ是平滑因子。

③求和層。

每个节点用（4）式计算样本层输入的总和值

其中C是类的总数。

④输出层。

输出层中的节点通过贝叶斯策略决定每个输入样本x的类，训练中需要选择的主要因素是平滑因子σ。

1.3 超图

超图是传统图形理论的推广，通过超图可以将真实世界的实体之间的高阶关系用直观的方式表达出来。从数学上讲，超图可以定义为H={X，E}，其中，X={x1，x2，…，xn}为非空有限的顶点集合，E={E1，E2，…，En}为X的非空子集，称为超边[4]。下面给出了有关超图和Helly性质的基本定理。

定理1 对于一个给定的超图H={X，E}，超边集合E？哿X，它是H的相交子集，其中E不为空且E中的超边两两相交。

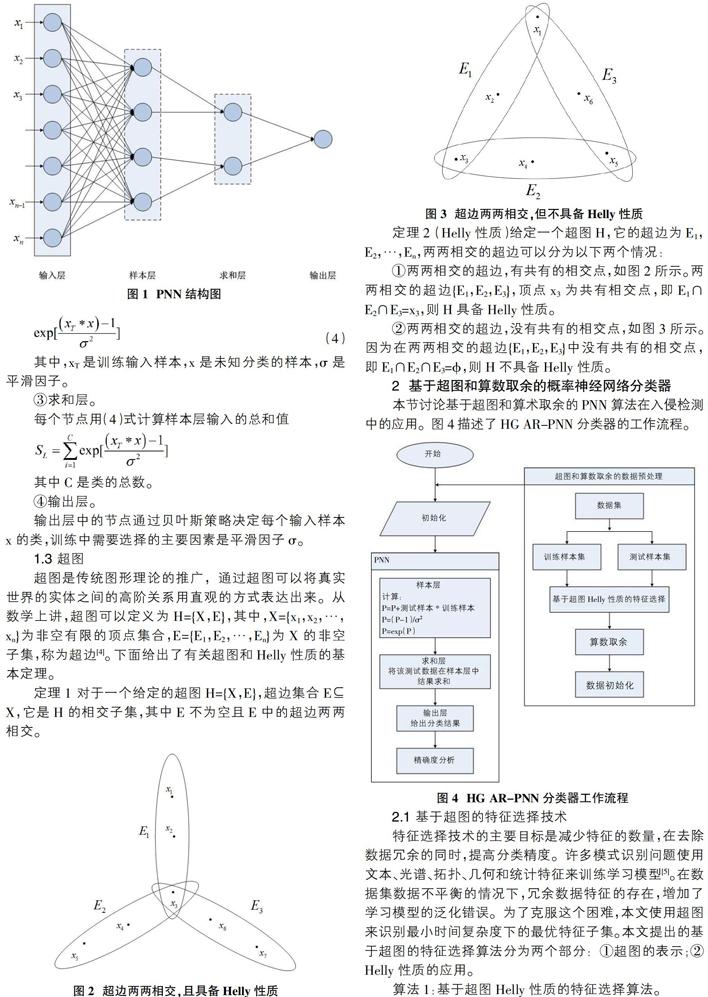
定理2 （Helly性质）给定一个超图H，它的超边为E1，E2，…，En，两兩相交的超边可以分为以下两个情况：

①两两相交的超边，有共有的相交点，如图2所示。两两相交的超边{E1，E2，E3}，顶点x3为共有相交点，即E1∩E2∩E3=x3，则H具备Helly性质。

②两两相交的超边，没有共有的相交点，如图3所示。因为在两两相交的超边{E1，E2，E3}中没有共有的相交点，即E1∩E2∩E3=？准，则H不具备Helly性质。

2 基于超图和算数取余的概率神经网络分类器

本节讨论基于超图和算术取余的PNN算法在入侵检测中的应用。图4描述了HG AR-PNN分类器的工作流程。

2.1 基于超图的特征选择技术

特征选择技术的主要目标是减少特征的数量，在去除数据冗余的同时，提高分类精度。许多模式识别问题使用文本、光谱、拓扑、几何和统计特征来训练学习模型[5]。在数据集数据不平衡的情况下，冗余数据特征的存在，增加了学习模型的泛化错误。为了克服这个困难，本文使用超图来识别最小时间复杂度下的最优特征子集。本文提出的基于超图的特征选择算法分为两个部分：①超图的表示；②Helly性质的应用。

算法1：基于超图Helly性质的特征选择算法。

输入：

f={f1，f2，…，fm}//所给数据集的m个特征

s={s1，s2，…，sn}//所给数据集的n个样本

c={c1，c2，…，ck}//所给数据集的k个类

输出：

fs最优特征子集

算法：HG（f，s，c，fs）：//利用欧式空间构建超边

//利用Helly性质选取最优特征子集

在初始阶段，通过对各样本的拓扑和几何关系得到超图的边，超图中的超边和顶点，分别对应数据集中的样本和特征。本文用基于欧氏空间度量的最小距离算法来构建每个类的边。

接下来，以递归的方式将超图的Helly性质应用于相交的边，而不相交的边所包含的特征将被忽视掉。由于超图Helly性质的应用，最优特征子集所产生的时间复杂度是最小的。

2.2 基于算术取余概率神经网络的分类器

一般来说，学习模型的工作效率取决于它能否对未知行为进行高精度的分类。人工神经网络作为一种学习模型，它在许多数据分析应用中发挥着重要作用。人工神经网络在不断改进中得到进化，如前馈神经网络、径向基神经网络、递归神经网络等，它们在提高了检测效率的同时也减少了训练时间，其中概率神经网络PNN将基于核的计算和RBF网络集成到统一的框架中，由于没有数据的交互，它能够快速的训练学习。在分类过程中，PNN将概率密度函数值和贝叶斯策略下最小期望风险值叠加。PNN在训练数据集上对已标记数据的概率值进行训练操作，而在测试数据集上基于未知样本对每个类的最高估计概率对其进行分类操作，然而对已标记数据的核函数计算是高度计算密集型的。

对于现有的神经网络分类器的不足，本文提出了一种基于算术取余的PNN分类器，算术取余的思想来源于群论中关于乘法模和加法模的两个基本定理，即n个数1，2，…，n的模相加或是相乘，而这些在除法中得到的余数显示了数字的物理特征。据观察，利用算术取余进行样本训练，明显改善了PNN的分类性能。因此为更大程度地加强PNN性能，首先利用基于超图的特征选择技术获得最优特征子集，再运用算术取余PNN训练数据集。

算法2：基于超图和算数取余的概率神经网络算法。

输入：

类的总数Tclass

训练集样本数Strain

特征向量fs

平滑因子σ

输出：

测试样本分类结果Classify

HG AR-PNN分类器算法过程如下：①初始化L，Sum，Classify和ε。②在原始数据集中，随机选择若干样本作为训练样本集和测试样本集，并根据算法1，在训练样本集中得到最优特征子集。③接下来，测试数据集中样本特征向量与训练数据集中每个类的样本特征向量的乘积为P，再对P应用平滑因子σ和指数因子exp进行计算，然后再将P值求和。④最后，在决策层，P值最大者即为该测试样本的分类结果。

3 实验结果及讨论

3.1 基准数据集

KDDCUP99数据集是一个被用来作为实验验证的标准的不均衡网络入侵数据集。它由500万个网络连接记录组成，每个记录都有42个属性，其中41个属性为基础属性，如表1所示，剩下的一个属性为决策属性，即标记该条记录是正常或是攻击类型。除了正常数据外，KDDCUP99数据集共有22种类型的攻击，它们分为四大类：DOS，U2R，R2L，Probe，如表2所示。KDDCUP99数据集的各类样本分布是不均衡的，如DOS攻击是大量的，而U2R，R2L，Probe则相对较少[6][7]。正是该数据集的不均衡性，使它更适于本文所讨论的问题。

3.2 实验过程

本文在i5处理器，Windows 7操作系统下，运行MATLAB6.5实施算法HG AR-PNN。实验分为三个阶段：①数据预处理；②训练样本集和测试样本集的准备；③结果评价。

在初始阶段，由于KDDCUP99数据集是十分庞大的，因此，我们随机从中选取训练样本和测试样本。本文选取的训练样本数和测试样本数如表3所示。

在接下来的阶段，我们先对样本中的字符型属性转化为整数型属性，再将每个样本的41条基础属性做归一化处理，即。最后，将HG AR-PNN的分类性能与已有的分类器（如随机森林、贝叶斯、MLPNN、BPNN等）进行比较，评价标准如下：

TP：表示实际上是攻击，且被分类器正确识别为攻击的样本数。

TN：表示实际上是正常，且被分类器正确识别为正常的样本数。

FP：表示實际上是攻击，而被分类器错误识别为正常的样本数。

FN：表示实际上是正常，而被分类器错误识别为攻击的样本数。

检测率：

误警率：

准确率：

除了这些评价标准外，稳定性也被认为是评价IDS性能的重要标准之一[8]，HG AR-PNN分类器的稳定性是通过训练成功的样本比例决定的。

稳定性=

3.3 实验结果及讨论

本文对基于超图的特征选择技术得到的特征向量归一化算数取余处理，并用处理后的特征向量训练PNN分类器，最后，将HG AR-PNN与现有分类器的分类性能进行了比较，如表4所示。

从实验结果分析，对于常见样本来说，HG AR-PNN的性能与现有的其他分类器是类似的，如正常样本、DOS、Probe等。而对于出现不频繁的攻击，如U2R、R2L等，HG AR-PNN的检测率和准确率都高于其他分类器，而误警率也明显偏低。HG AR-PNN不仅能够更好地辨别特征之间的差异，还能为小样本数据提供良好的分类性能。综上所述，超图的Helly性质和对最优特征子集进行算数取余能够提高PNN的分类性能，且对高维不平衡数据集依然有着良好的分类效果。

另外，HG AR-PNN在训练时间和稳定性方面也优于其他分类器，从表可知，HG AR-PNN的稳定性高于现有的神经网络分类器，虽然HG AR-PNN的训练时间比一些分类器的训练时间要长，但在现有的神经网络分类器中却是训练时间最少的。因此，本文提出的HG AR-PNN分类器在保证良好的分类精度的前提下，有效地降低了时间复杂度和空间复杂度。

4 结论

随着网络技术的迅速发展，网络信息安全成为一个极具挑战性的研究领域。IDS作为网络防御的一个重要角色，它对网络中流量进行实时监视，以识别各种网络安全漏洞。随着机器学习技术的出现，智能化和鲁棒性IDS的研究不断发展，而学习模型的性能取决于数据集的性质和学习体系结构的稳定性。本文提出了基于超图Helly性质和算数取余概率神经网络的入侵检测分类器模型。实验表明，HG AR-PNN相比现有分类器的优势在于它拥有较高的稳定性，且对小样本攻击数据依然有较高的检测率、准确率和较低的误警率。

参考文献：

[1]曹元大.入侵检测技术[M].北京：人民邮电出版社，2007.

[2]郭春.基于数据挖掘的网络入侵检测关键技术研究[D].北京：北京邮电大学，2014.

[3]沈夏炯，王龙，韩道军.人工蜂群优化的BP神经网络在入侵检测中的应用[J].计算机工程，2016（02）.

[4]王超杰.超图理论算法研究及其在图像分类中的应用[D].厦门：厦门大学，2014.

[5]SH Kang，KJ Kim.A feature selection approach to find optimal feature subsets for the network intrusion detection system[J].Cluster Computing，2016，19（1）：1-9.

[6]吕银均.基于数据挖掘的入侵检测系统研究与实现[D].杭州：浙江工业大学，2014.

[7]王翔，胡学钢.高维小样本分类问题中特征选择研究综述[J].计算机应用，2017（09）.

[8]MAM Hasan，M Nasser，B Pal，S Ahmad.Support Vector Machine and Random Forest Modeling for Intrusion Detection System （IDS）[J].Journal of Intelligent Learning Systems & Applications，2014，6（1）：45-52.