基于双因子改进型粒子群算法的混合滤波系统的多目标优化设计

黄 彬，王 杰，曹人靖，黄冬明，牛传凯，刘长智，王 军，李云涛



基于双因子改进型粒子群算法的混合滤波系统的多目标优化设计

黄 彬1,2，王 杰1，曹人靖2，黄冬明2，牛传凯2，刘长智2，王 军2，李云涛2

（1. 上海交通大学电子信息与电气工程学院，上海 200240；2. 明阳智慧能源集团股份公司，广东 中山 528467）

大容量混合滤波系统的应用前景十分广阔，其滤波器组的参数优化，尤其是无源滤波器的参数设计对综合性能的影响很大。本文提出基于双因子改进型粒子群优化算法的混合滤波系统中无源滤波器组的多目标优化设计方法。通过将加速因子和交叉因子引入优化算法，针对无源滤波器的多目标优化，高效搜索参数空间以获得最优解。与以往的优化设计相比，带双因子的改进型粒子群算法采用自适应的惯性权重，交叉因子增加了粒子的多样性，克服了算法寻优过程中易局部收敛等问题，提高其全局搜索能力。而收缩因子可以加快PSO的运算速度，明显提高了算法的寻优速度。测试结果表明利用该算法设计的混合型滤波系统具有较强的鲁棒性。

混合型滤波器；无源滤波器组；参数优化；双因子改进型粒子群优化算法；加速因子；交叉因子

0 前言

电力推进方式逐渐成为大型船舶的重要发展趋势，但也给船舶电网带来了更多的谐波污染。对船舶电力系统来讲，谐波使发电机的效率降低，导致绝缘老化、使用寿命缩短。谐波还会引起船舶继电保护和自动控制装置的可靠性降低，产生误动作，对通信设备和电子设备产生严重干扰。现有的电力系统谐波治理装置中，传统的谐波治理方法是采用无源滤波器PPF(Passive Power Filter)，其参数如果设计不当,不仅滤波效果不好，而且可能造成系统无功功率过补偿以及与电网系统阻抗发生串、并联谐振等问题[1]。有源电力滤波器APF(Active Power Filter)滤波效果较好，但初期投资较高且滤波容量较小。混合滤波系统HPFS(Hybrid Power Filter System)可以以较低的成本获得较好的滤波效果和稳定性，实现优势互补，具有较好的研究价值和广阔的应用前景。以往的HPFS系统中PPF的设计一般是根据工程经验或简单的技术经济指标来选择参数，对复杂的系统拓扑、无功补偿、性价比高、谐波畸变率最小等多目标问题未加以考虑，可能出现PPF的参数与实际电力系统不匹配等情况[2-5]。本文将性价比、无功补偿、谐波含量等目标与滤波器参数设计紧密结合起来，提出基于双因子改进型粒子群算法的混合型滤波器的无源滤波器组优化的参数设计方法，可以有效解决上述多目标优化问题。

1 混合滤波系统HPFS的原理

混合滤波系统HPFS由多组分别调谐于主要谐波频率的单调谐滤波器和有源滤波器串联构成，如图1所示。通过旁路谐波源产生的谐波电流对电网起到带阻和低通滤波的作用。APF通常由电压型逆变器构成，经变压器耦合与PPF串联后并联在电网上，其作用是改善PPF的滤波效果和抑制串、并联谐振。在理想情况下，谐波电流全部流过HPFS。APF的额定容量主要取决于谐波电流在PPF上产生的谐波电压幅度，并最终取决于PPF的滤波效果，即PPF参数优化的程度。显然，在同等条件下，HPFS中APF的额定容量较“纯APF”明显地减小，而且PPF的参数优化程度越高，APF的额定容量就愈小，从而确保HPFS的低成本和高性能。

HPFS设计是典型的非线性，多目标优化问题，涉及技术、经济、安全性等多方面。对其中的PPF，首先应根据谐波源的特性，即谐波次数和含量等，参照谐波限制的有关标准，选定PPF的结构和滤波参数，包括单调谐滤波器的组数和每组各自的谐振频率等。其次，应以综合效益最佳为原则，并考虑元件容差、系统频率等实际因素，最终确定最优的PPF参数组合和元件规格，即要使PPF的滤波性能最佳。既在满足预期指标的基础上尽可能地减小残余的谐波含量，又要符合船舶电力系统复杂工况的运行要求。

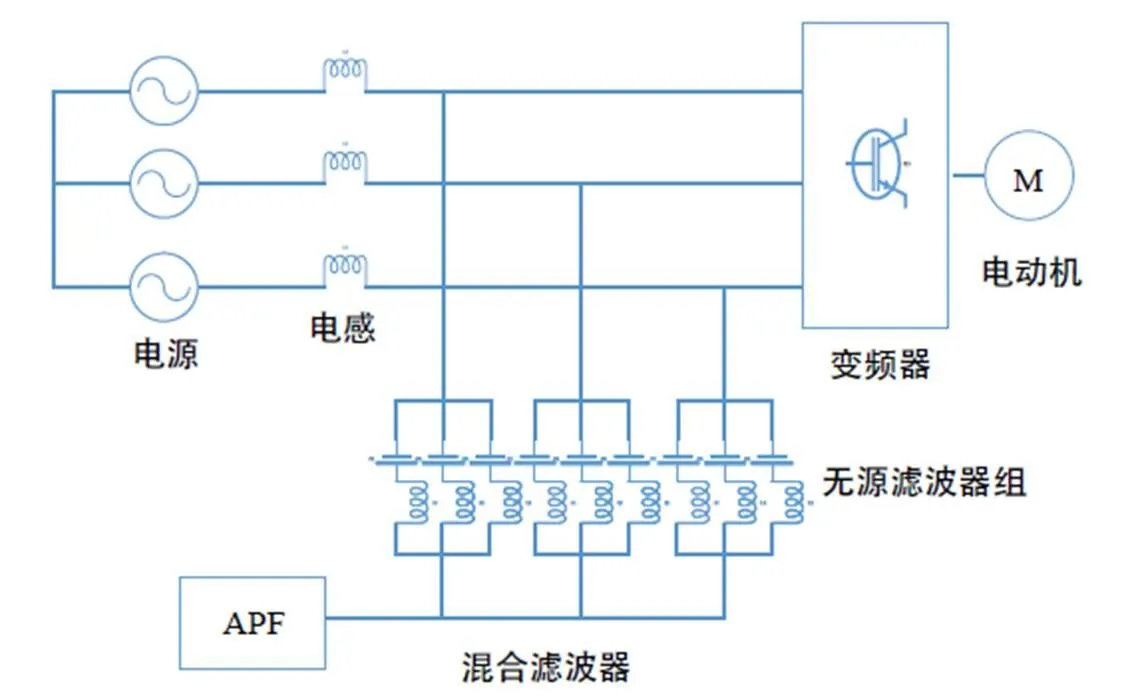
图1 并联型HPFS模型

HPFS中的PPF参数优化问题可以归结为在一些等式及不等式约束条件下，求解多目标函数极小值的问题。具体地说，首先确定等式约束条件，如电气网络的潮流方程。不等式约束条件，如谐波电压畸变率和电流畸变率，以及交流系统无功平衡、无功补偿等约束条件，建立合理的综合目标适应度函数，通过相应算法，对多目标综合函数的最小值进行求解，优化PPF参数。在滤波器设计问题上，单以一个指标性能来求解滤波器参数，很难完整地评价设计的合理性及质量的优劣。因此，在滤波器规划时，制定目标函数应综合考虑电流畸变率最小、电压畸变率最小、滤波器设备总费用最小、是否无功功率过补偿等多个指标，是一个多目标、含约束条件的非线性规划问题。

2 基于遗传交叉因子和收缩因子的双因子改进型粒子群算法

粒子群优化(Particle Swarm Optimization)算法是由Kennedy和Eberhart提出的一种基于群搜索(Swarm Search)的演化计算(Evolutionary Computation)技术。与其他进化算法相类似，兼有进化计算和群智能的特点。该算法模拟一鸟集群飞行觅食的行为，通过鸟之间的集体协作与竞争使群体达到目的[6-10]。

PSO算法属于群体智能算法，是全局的随机搜索优化方法，不受函数约束条件的限制。搜索过程不是从单个个体开始，而是从问题解的一个集合开始的，将搜索重点集中在性能高的部分，具有隐含并行搜索特性，可以减小陷入局部极小值的可能性[11-15]。PSO算法中的粒子共享当前搜索到最优点的信息，而且只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。

PSO算法的数学描述为：设搜索空间为D维，总粒子数为；

粒子的速度和位置根据如下公式进行变化：

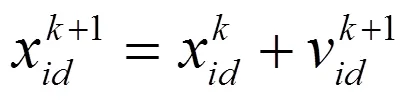
对于高维的复杂优化问题,在标准的PSO算法设计时若加速因子、最大速度等参数太大，粒子群可能错过最优解，导致不收敛。而且PSO算法执行到后期，收敛速度会变慢，并且可能存在着搜索精度较低，易发散及陷入局部最优等问题。

为了克服标准PSO算法的不足，本文提出基于遗传交叉因子和收缩因子的改进粒子群算法。交叉因子增加了粒子的多样性，克服了标准粒子群算法易陷入局部最优点的不足，提高了其全局搜索能力。而收缩因子可以加快PSO的运算速度，使算法收敛性强，有较快的收敛速度。

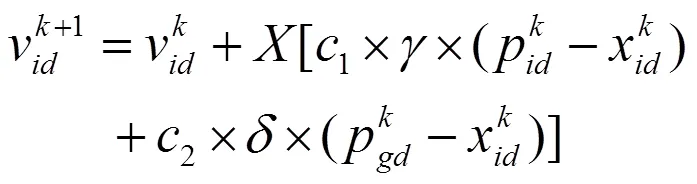
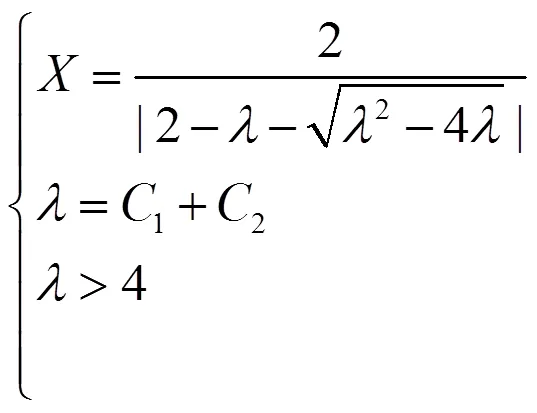
图2 收缩因子X趋势图

引入交叉因子，每次迭代选取适应度好的一半粒子直接进入下一代，后一半粒子作为待交叉因子进行两两随机配对。若粒子群大小为，则共有(/2)对相互配对的个体组。对每对相互配对的粒子，随机设置交叉点，即基因交换位置。对每一对相互配对的粒子，在其交叉点处相互交换，从而产生两个新的子代。再和父代粒子作比较，选择适应度值高的一半进入下一代。以保持种群的粒子数目不变。然后对所有的粒子进行更新。这样既可以加快收敛速度，又可以增加粒子多样性，避免局部最优化，如图3所示。

选取目标函数作为适应度判断函数，则适应度排序为：

图3 带双因子的PSO算法流程图

3 目标函数优化变量及适应度选择

一般地，多目标优化问题可归结为如下的多目标极小化模型[16-18]：

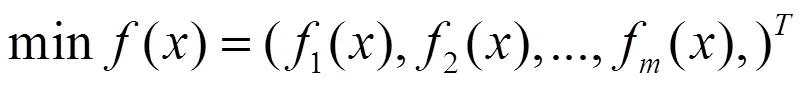
PPF优化需要考虑的约束条件如下：

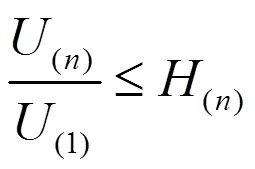
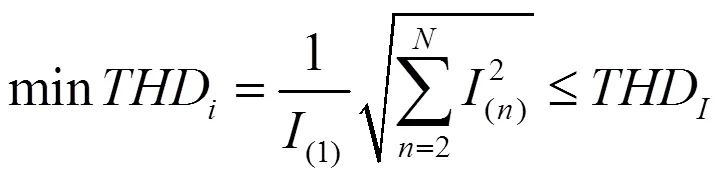
其中，cos是系统本身的功率因数，sin(max)、sin(min)为PPF提供基波无功的功率因素上下限。

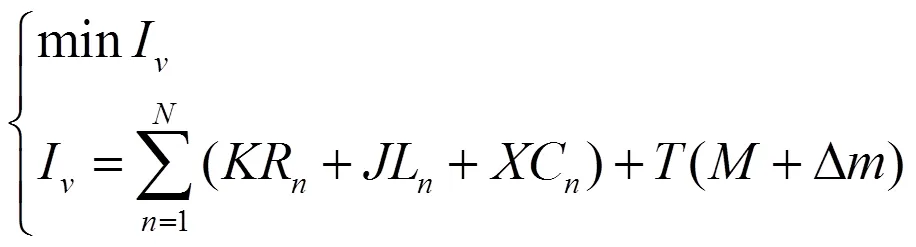
考虑目前大型船舶电网一般采用12脉变频器，大型船舶的HAPF中的PPF多选用单调谐滤波器组，将各单调谐滤波器的品质因素定为=60，既保证了滤波器对频率的选择性，又保证了滤波器在频漂及参数漂移下的滤波效果。引入参数：

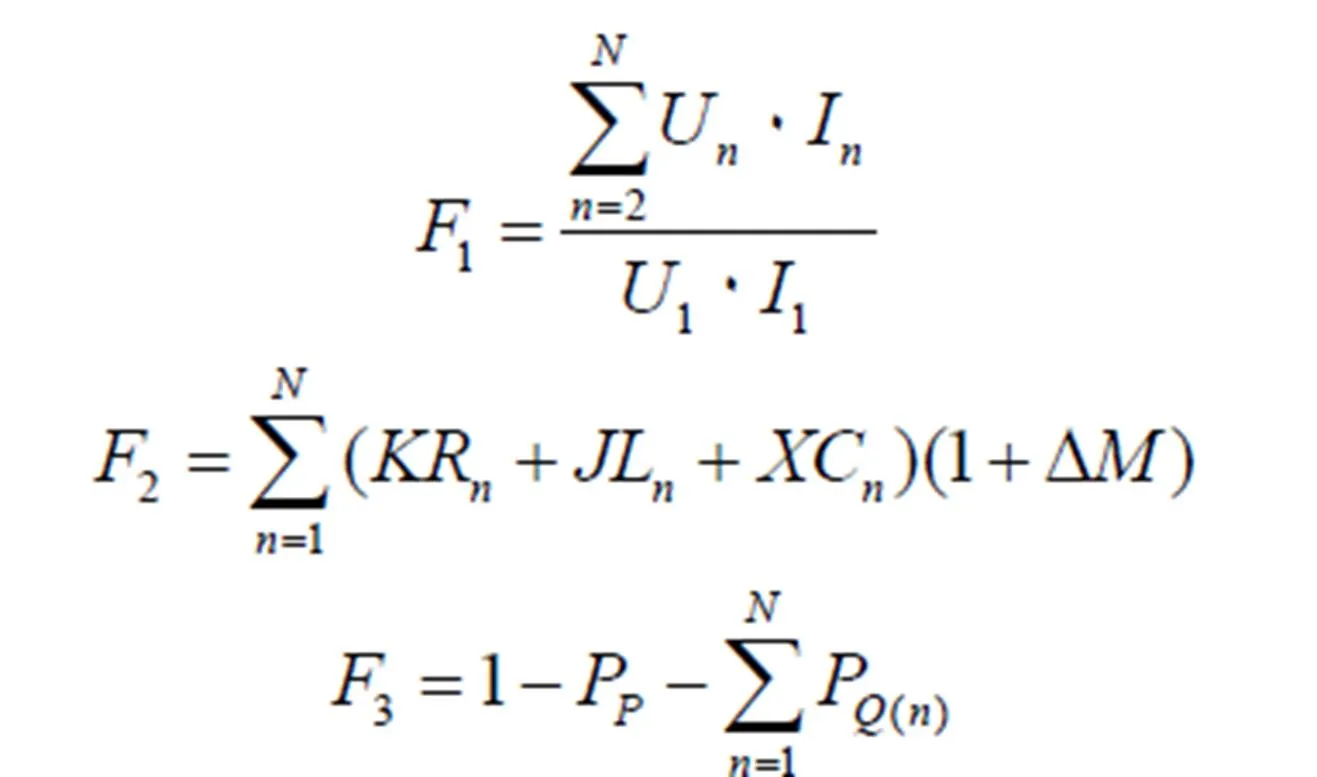
统一的适应度函数为：

带双因子的PSO算法计算步骤如下：

（2）对所有粒子编码，并随机初始化其位置和速度；

（3）根据式（5）计算粒子的适应值；

（4）按照适应度优劣对粒子群进行排序，选取后一半粒子放入池中，进行交叉因子操作。

（5）交叉因子操作结束，选取池中适应度好的前一半粒子进入下一代，以保持整个粒子群规模。

（6）根据式（2）、（3）更新粒子的速度和位置；

（8）重新计算粒子的适应度；

（10）判断是否满足中止条件，若满足，算法中止。否则，转第（3）步。

4 算法实例1

图4 某大型船舶电力推进系统模型

其中6.6kV电网系统的主要谐波见表1，总的谐波畸变率为5.81%，总的功率因数为92.9%。电压电流波形如图5、6所示。电压谐波次数及含量如图6所示。

表1 某LNG船舶的谐波电压频谱

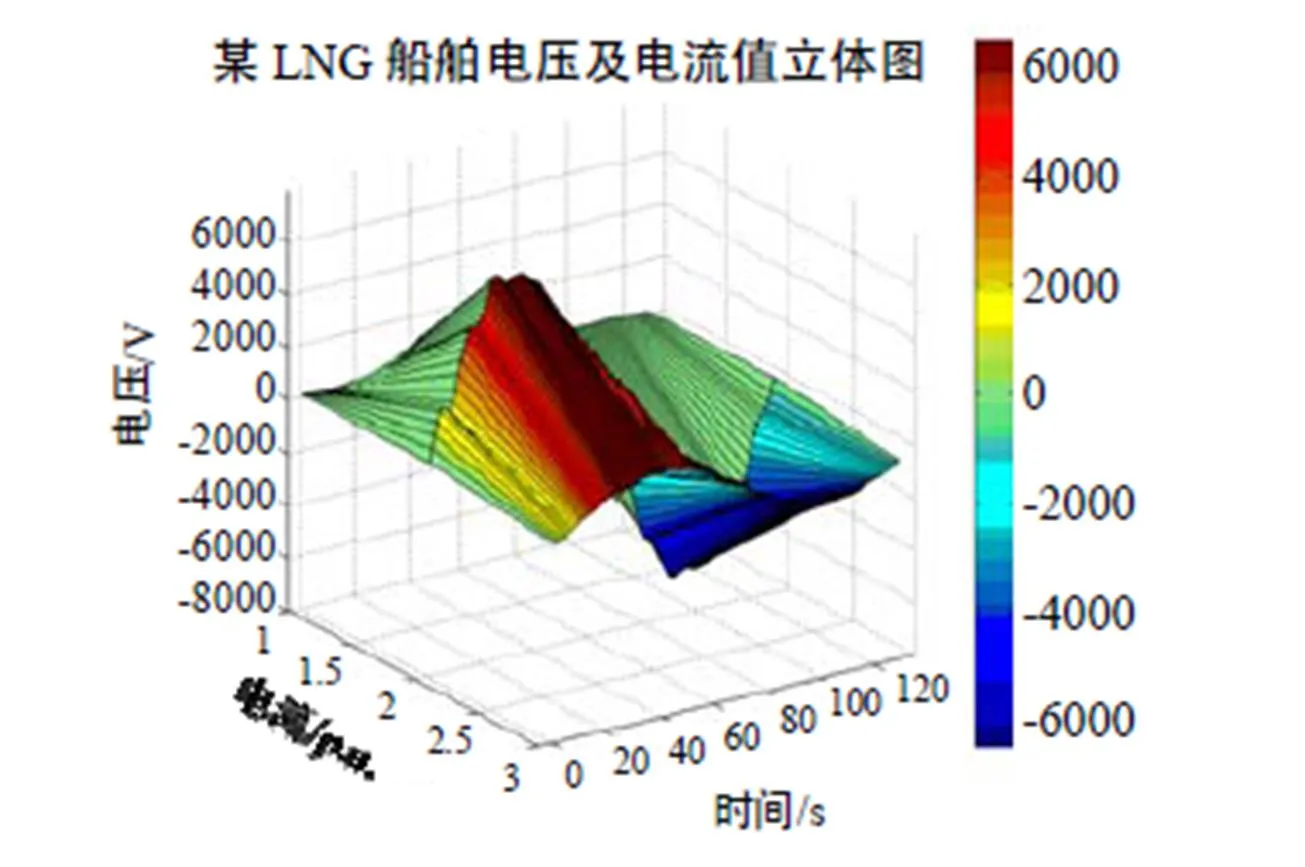
图5 LNG船舶电压电流波形图

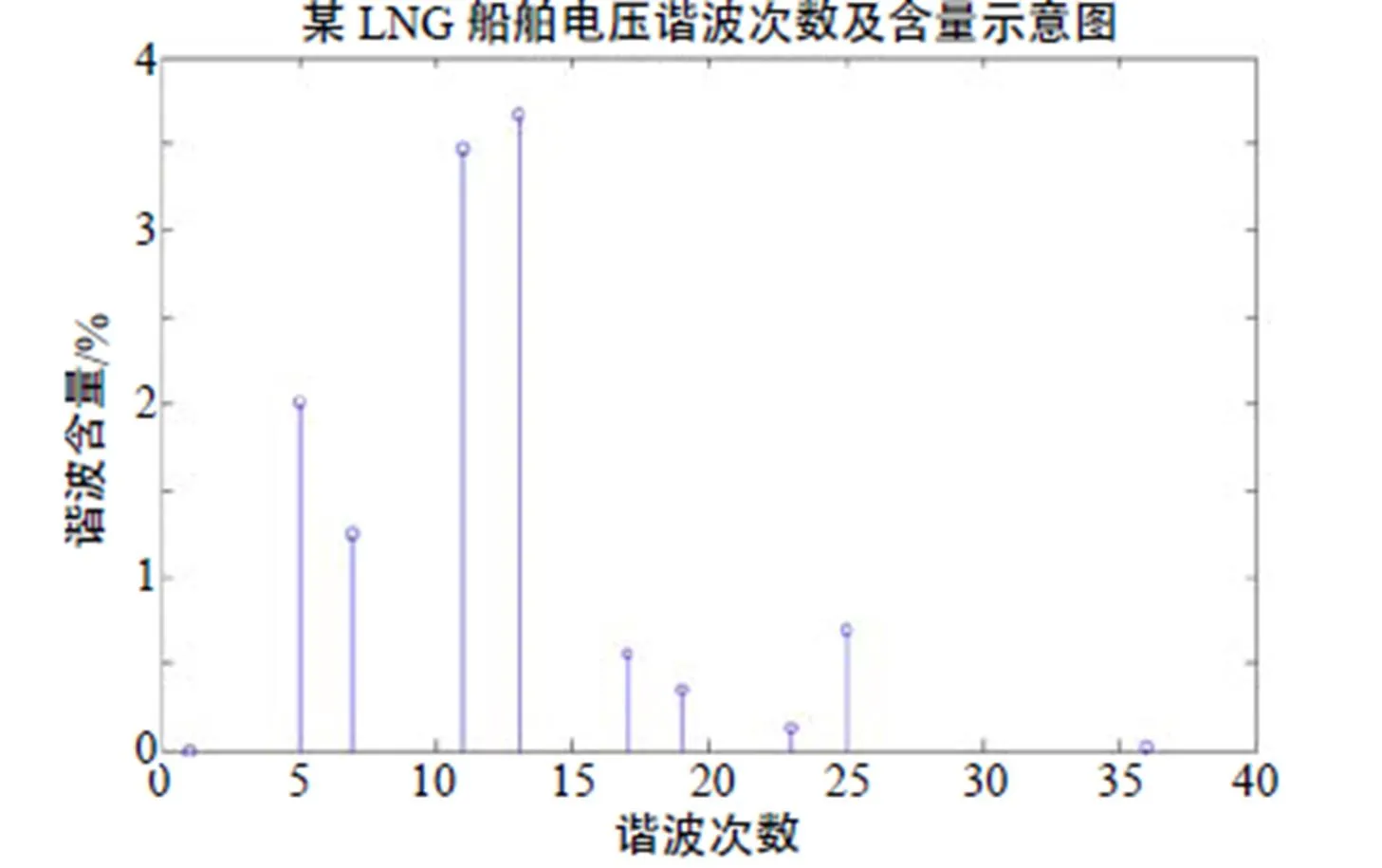
图6 LNG船舶电压谐波分析图

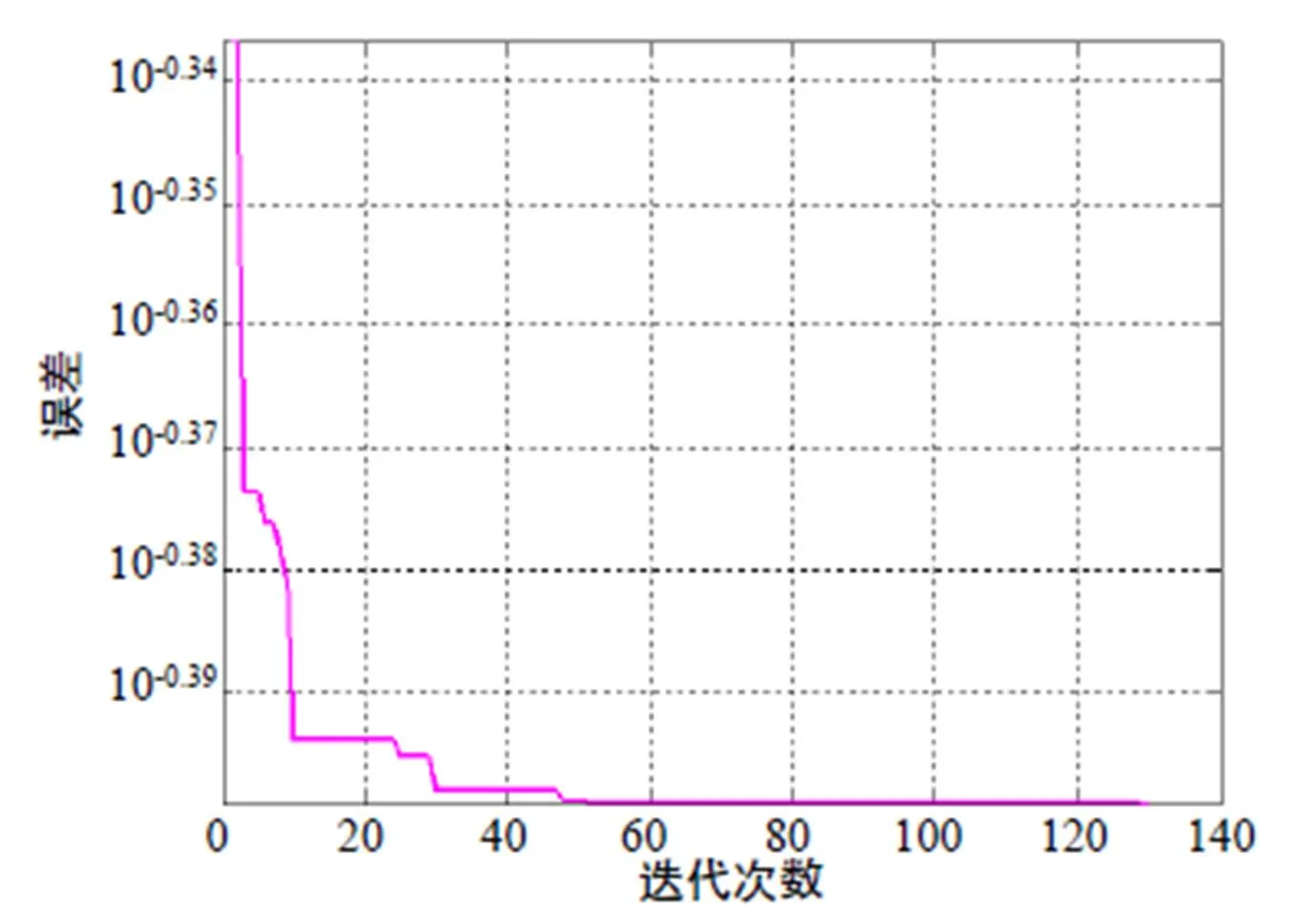
图7 带收缩因子的PSO算法迭代次数

经过135次迭代，无源滤波器参数见表2。滤波后电压电流波形如图8所示，滤波后电压谐波次数及含量如图9所示。

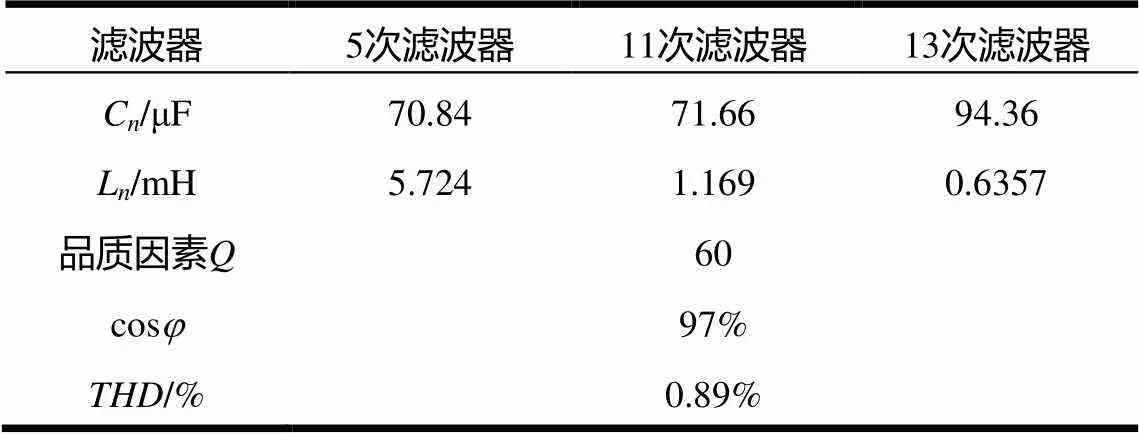
表2 无源滤波器参数及结果

图8 滤波后的电压与电流波形图

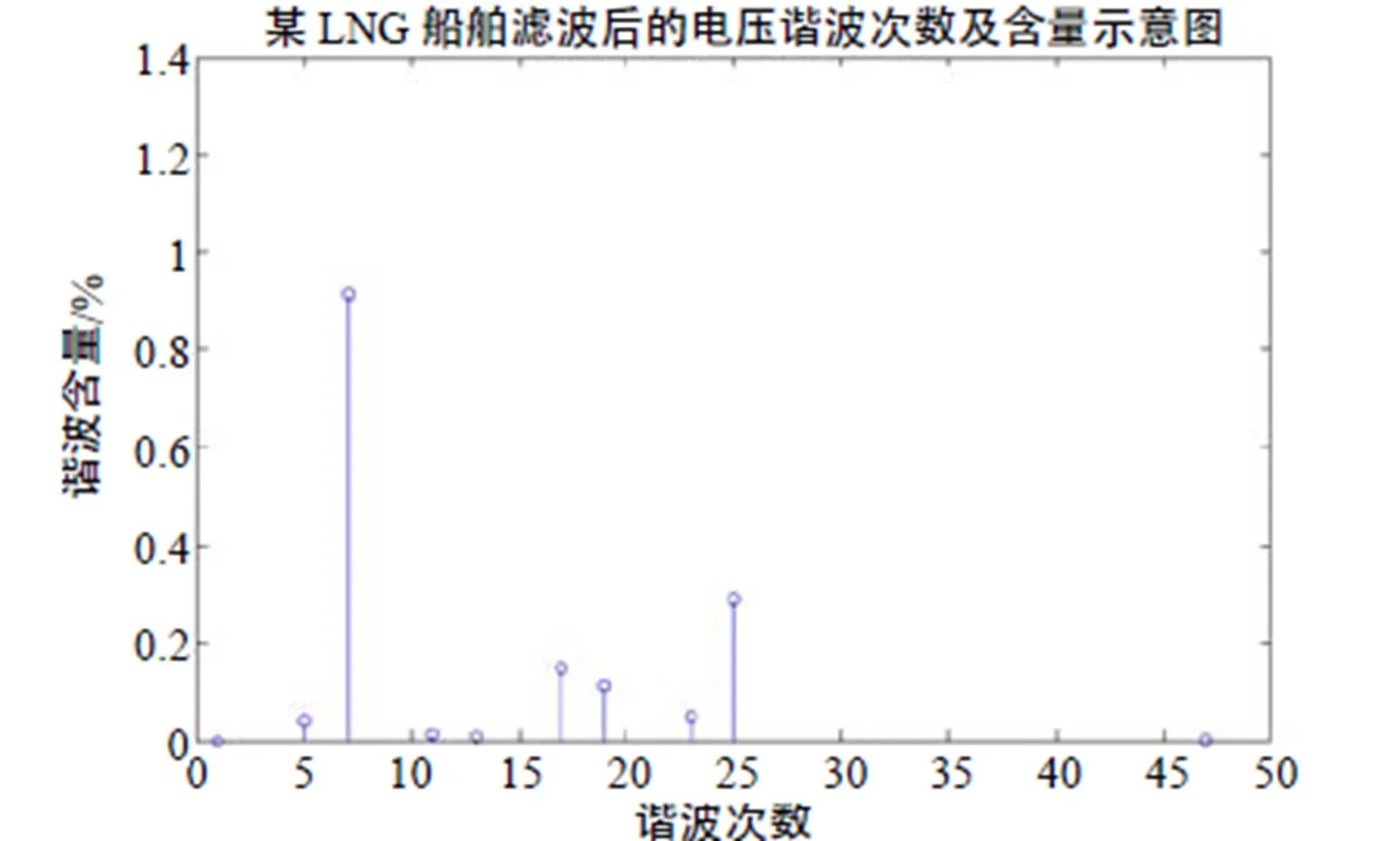
图9 滤波后的电压谐波分析图

将按照上述方法设计的无源滤波器组的混合型滤波器应用到实际系统中，计算及实际测试结果均表明，在各种工况下其谐波的总含量低于0.89%，满足国家标准，如表2所示。说明设计的滤波系统具有很好的滤波效果。

5 算法实例2

以某大型风力发电机网测LCL滤波器设计优化为例进行说明，仿真模型如图10所示。

仿真参数为：额定容量3MW，电网线电压690V，直流母线电压1100 V，开关频率5kHz。利用经验计算求解法（传统算法）和基于双因子改进型优化算法设计LCL 滤波器参数见表3。

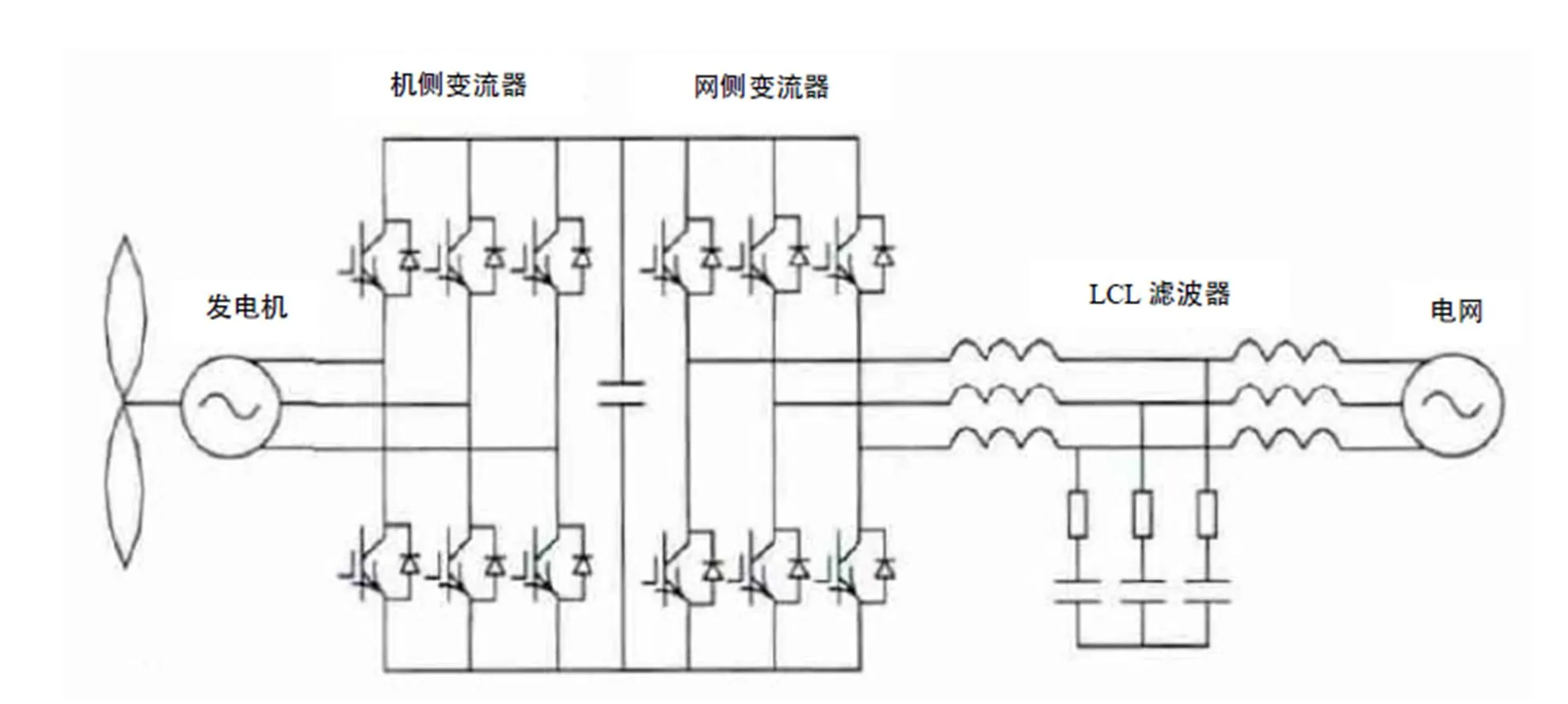
图10 大型风力发电机仿真系统

表3 LCL滤波器参数

把传统算法和基于双因子改进型优化算法设计的LCL滤波器分别代入仿真模型，并网逆变器侧输出电流波形分别如图11(a)和图11(b)所示。

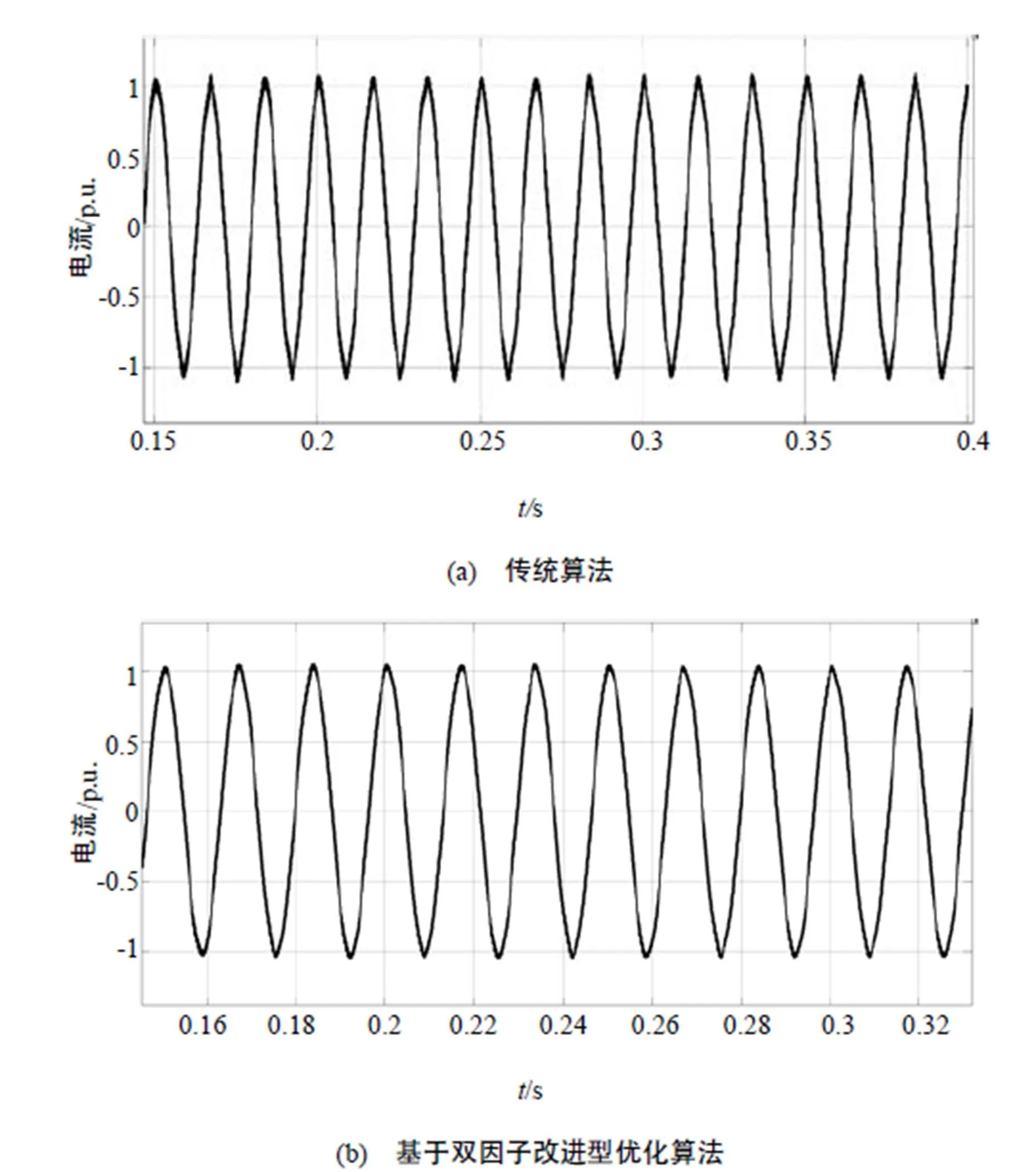
图11 网侧电流波形

由图11可知，两者都能对并网逆变器的谐波起到抑制作用，而且基于双因子改进型优化算法设计的LCL滤波器滤波效果更为明显。

为了进一步验证滤波性能，对比分析两种算法的网侧电流的频谱并计算出对应的谐波畸变率()。通过FFT计算，传统算法设计的LCL滤波器滤波后网侧电流的为2.17%，而基于双因子改进型优化算法设计的LCL滤波器滤波后网侧电流的为1.03%，谐波畸变率明显减小，说明基于双因子改进型优化算法在LCL滤波器参数优化设计的有效性。

6 结论

本文针对混合滤波系统中无源滤波器部分，采用带双因子的改进型粒子群优化算法进行多目标优化设计，所用优化方法与己有优化设计方法相比，算法优良，参数少、容易实现，寻优能力强。该方法已在多个大型系统中得到应用，所设计的滤波系统具有优良的性能与鲁棒性。

[1] Lu L, Luo Q, Liu J Y, et al. An Improved Particle Swarm Optimization for Reconfiguration of Distribution Network[J]. Automation of Electric Power Systems, 2008, 4(7):453-457.

[2] 李辉, 张安, 赵敏,等. 粒子群优化算法在FIR数字滤波器设计中的应用[J]. 电子学报, 2005, 33(7):1338-1341.

[3] Hou Z X. Wiener model identification based on adaptive particle swarm optimization[C]// International Conference on Machine Learning and Cybernetics. IEEE, 2008:1041-1045.

[4] Wang Z, Li J, Zhou M, et al. Research in capacitated vehicle routing problem based on modified hybrid particle swarm optimization[C]// IEEE International Conference on Intelligent Computing and Intelligent Systems. IEEE, 2009:289-293.

[5] 罗伟原. 基于粒子群改进算法的无源电力滤波器优化设计[D]. 湖南大学, 2009.

[6] Inthachot M, Supratid S. A Multi-Subpopulation Particle Swarm Optimization: A Hybrid Intelligent Computing for Function Optimization[C]// International Conference on Natural Computation. IEEE Computer Society, 2007:679-684.

[7] Li R, Guo Y, Xing Y, et al. A Novel Multi-Swarm Particle Swarm Optimization Algorithm Applied in Active Contour Model[M]. IEEE, 2009.

[8] Fan C, Wan Y. An adaptive simple particle swarm optimization algorithm[C]// Control and Decision Conference, 2008. Ccdc. IEEE, 2008:3067-3072.

[9] Niu D, Xing M. Research on Neural Networks Based on Culture Particle Swarm Optimization and Its Application in Power Load Forecasting[C]// International Conference on Natural Computation. IEEE, 2007:270-274.

[10] Asl L B, Nezhad V M. Improved Particle Swarm Optimization for Dual-Channel Speech Enhancement.[C]// International Conference on Signal Acquisition and Processing. IEEE, 2010:13-17.

[11] Brown R E. Impact of Smart Grid on distribution system design[C]// Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the, Century. IEEE, 2008:1-4.

[12] 何娜, 黄丽娜, 武健,等. 基于粒子群优化算法的混合有源滤波器中无源滤波器的多目标优化 设计[J]. 中国电机工程学报, 2008, 28(27):63-69.

[13] Wang W, Wu J M, Liu J H. A Particle Swarm Optimization Based on Chaotic Neighborhood Search to Avoid Premature Convergence[C]// International Conference on Genetic and Evolutionary Computing. IEEE, 2010:633-636.

[14] Chen Y P, Peng W C, Jian M C. Particle Swarm Optimization With Recombination and Dynamic Linkage Discovery[M]. IEEE Press, 2007.

[15] Yang B, Chen Y, Zhao Z, et al. A Master-Slave Particle Swarm Optimization Algorithm for Solving Constrained Optimization Problems[C]// Intelligent Control and Automation, 2006. WCICA 2006. The Sixth World Congress on. IEEE, 2006:3208-3212.

[16] Liu Z, Wang S. Hybrid Particle Swarm Optimization for Permutation Flow Shop Scheduling[C]// Intelligent Control and Automation, 2006. WCICA 2006. The Sixth World Congress on. IEEE, 2006:3245-3249.

[17] Hu J, Yu L, Zou K. Enhanced Self-Adaptive Search Capability Particle Swarm Optimization[C]// Eighth International Conference on Intelligent Systems Design and Applications. IEEE, 2008:49-53.

[18] Hsu C C, Gao C H. Particle swarm optimization incorporating simplex search and center particle for global optimization[C]// Soft Computing in Industrial Applications, 2008. SMCia '08. IEEE Conference on. 2009:26-31.

Multi-objective Optimization Design of Hybrid Filter Based on Improved Particle Swarm Optimization Algorithm with Two Factors

HUANG Bin1,2, WANG Jie1, CAO Renjing2, HUANG Dongming2, NIU Chuankai2, LIU Changzhi2, WANG Jun2, LI Yuntao2

(1. School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Ming Yang Smart Energy Group Co., Ltd., Zhongshan 528467, China)

The high-capacity hybrid filter will be applied very widely in the large ship. The optimization of parameters has great impact on its overall performance. In this paper, the multi-objective optimization method based on two-factor improved particle swarm optimization(PSO) algorithm is introduced in the design of passive filters group of the hybrid filter equipment, with the aim to resolve the current problems such as poor capacity and tardy response in optimization. With the application of acceleration factor and hybrid genes to multi-objective optimization, higher efficient search within the parameter space can be realized to obtain the optimal solution. Compared with the traditional optimal design, the improved PSO with two factors adopts self-adaptive inertia weight, which allows hybrid genes to diversify the particles and overcomes local convergence in the algorithm optimization process, and the capacity of overall search is enhanced consequently. Constriction factor can accelerate the computation speed of PSO, which improves the algorithm's searching speed greatly. Experiments indicate that filtering effects are improved and that the hybrid filters have good performance and robustness.

hybrid filter; passive filters group; parameter optimization; improved particle swarm optimization with two factors; acceleration factor; hybrid genes

TM761

A

1000-3983(2018)03-0053-08

2017-11-30

国家重大科技专项经费资助项目(2008ZX05027-003)；教育部新世纪优秀人才资助项目(NCET-08-0356)。

黄彬（1983-），毕业于上海交通大学，电力系统及其自动化专业，博士，现从事多能互补智慧能源、智慧城市等研究方向。