基于多物理场耦合的感应电机噪声分析

王 韬，孙玉田，王 倩，毕纯辉，苟智德



基于多物理场耦合的感应电机噪声分析

王 韬1，孙玉田1，王 倩2，毕纯辉1，苟智德1

（1. 哈尔滨大电机研究所，哈尔滨 150040；2. 哈尔滨理工大学，哈尔滨 150080）

感应电机的设计中，经常要对振动和噪声进行分析和评价。本文提出一种基于多物理场耦合的感应电机噪声分析和研究方法。将感应电机的电磁力通过谐响应分析与振动和噪声耦合起来，实现了对感应电机的振动和噪声的求解和计算。分析的结果与实测噪声验证吻合得非常好，证明了这种分析方法的准确性。

感应电机；槽配合；多物理场耦合；谐响应分析；振动；噪声

0 前言

目前，随着经济的逐步提高，我国对能源的需求也逐步加大，同时对节能与环保问题给予了极大的重视。在能源网络中，电机是难以或缺的一个重要枢纽。提高对电机的振动与噪声的要求，符合我国节能与环保的国策和长期科学的可持续发展需要。电机的噪声形成是一个复杂的物理过程，根据其形成的机理，一般可分为气动噪声、机械噪声和电磁噪声。本文仅针对感应电机的电磁噪声进行分析和研究。

众所周知，电机在发生电磁振动的同时形成电磁噪声，而电磁振动的产生是电机的气隙磁场在铁心中作用产生电磁力的结果。这个电磁力是一个旋转的力波，它可以分成径向和切向两个正交的分量。其中电磁力的径向分量会使电机的定子发生径向变形和振动，是电磁噪声产生的主要因素；同时电磁力的切向分量由于产生电磁转矩，则会使电机定子的齿部向其根部弯曲变形，是电磁噪声产生的次要因素[1,2]。如果电机的电磁设计中定、转子槽配合选取不合适，则会产生高频电磁噪声，同时也会增大电机的机壳和出线盒的振动和噪声[3]。因此本文重点研究不同的定转子槽配合下，电机的振动和噪声。本文研究的结论能够在电机设计时选择合适的槽配合，使铁心电磁力的力波频率避开定子的固有频率，从而有效降低电机的振动和噪声，对今后的电机设计将有重要指导意义[4]。

1 感应电机电磁力波分析

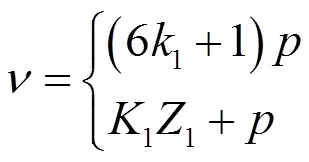
设转子槽数为2，转子齿谐波磁场次数为，则有

根据式（1）和式（2），假设定子绕组的次谐波磁场在转子感应出次谐波磁场，该转子磁场与定子绕组的次谐波磁场又相互作用，产生的径向力波阶数为

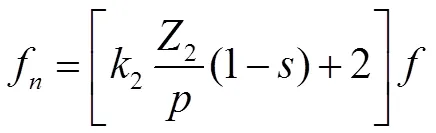
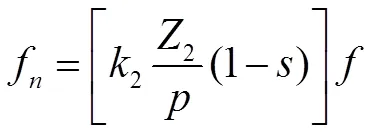
式（4）和式（5）中为转子的转差率。根据上面的分析可知，当力波次数为比较低的整数，同时产生这个次数力波的谐波磁场幅值比较大时，将会形成比较大的电磁噪声[5]。

为了进一步研究不同槽配合对感应电机振动的影响，本文设计了两台结构尺寸均相同、定子槽数也相同，仅仅转子槽数不同的电机[6]。假设1号电机的定、转子槽配合1/2为24/26，2号电机的定、转子槽配合1/2为24/31，两台电机基本参数见表1。

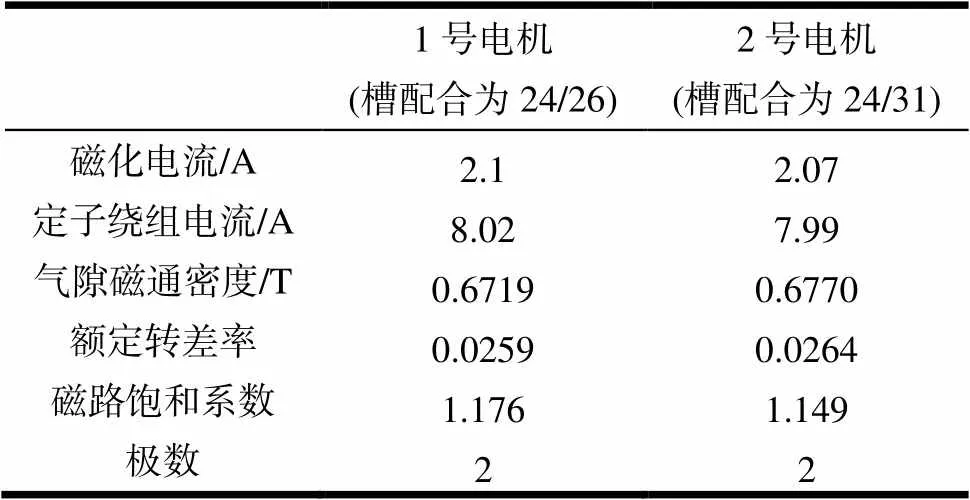
表1 不同槽配合方式的两台电机基本参数

两台槽配合不同的电机激振电磁力波次数分别如表2和表3所示。

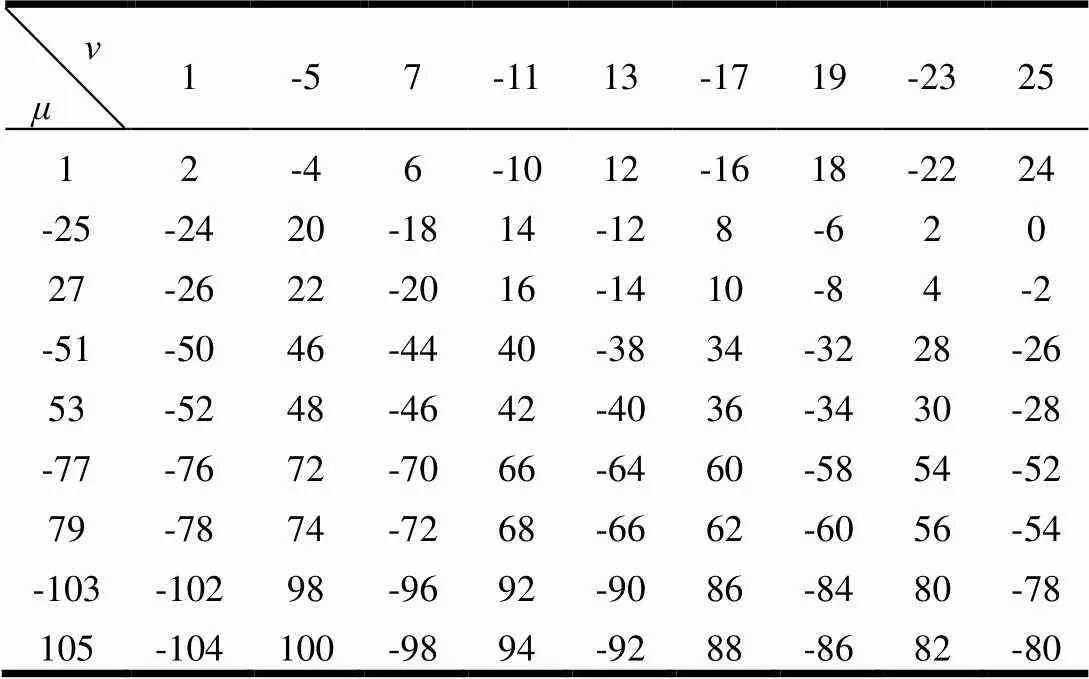
表2 1号电机的激振电磁力波次数(槽配合方式为24/26)

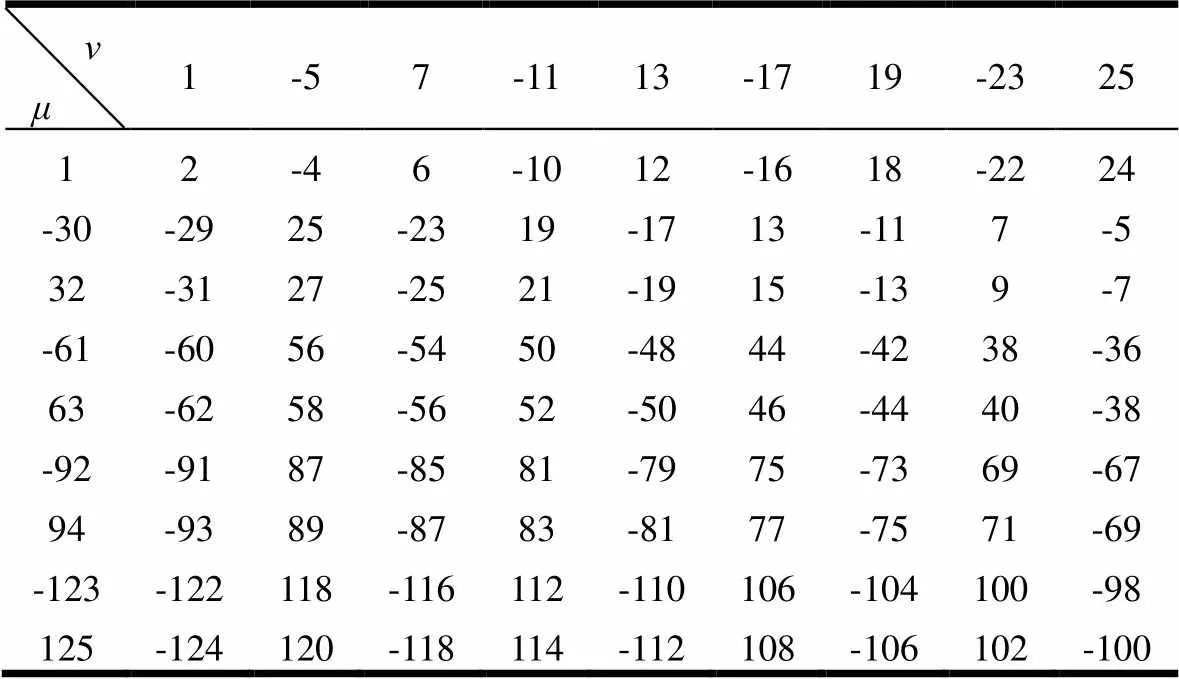
表3 2号电机的激振电磁力波次数(槽配合方式为24/31)

以上是对两台电机的振动和噪声进行了定性的分析。为了确定1号电机和2号电机两种不同槽配合方式哪一种更为合理，我们还需要对这两台电机定子的固有频率和振动特性进行计算。

2 感应电机不同槽配合方式的谐响应分析

对于一个自由度为的线性系统，表征其受到激振的振动过程的偏微分方程如下：

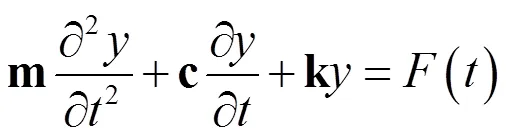
式（6）中，表示点位移的阶向量，()表示外部载荷向量，m表示阶质量矩阵，c表示阶阻尼矩阵，k表示阶刚度矩阵。

如果忽略系统的振动阻尼，式（6）将变为

对其求解将得到系统的固有频率和振动特性。据此，我们可以建立对于感应电机的模型。本文利用ANSYS Workbench平台进行多物理场的有限元耦合来求解1号电机和2号电机的振动和噪声。略去无载荷状态下的模态分析过程，其总体耦合过程如图1所示。

首先通过ANSYS Maxwell模块对定子齿部的电磁力进行求解，两台电机的齿尖所受电磁力的力密度分布如图2所示，同时可以得到该电磁力的径向分量和切向分量。

图2 1号电机和2号电机的定子齿部电磁力力密度分布

然后将得到的电磁力的径向分量和切向分量结果作为外部载荷加载给定子铁心模型，如图3所示。同时令两台电机的机壳作为边界条件，不考虑定子铁心与机壳之间的间隙，利用ANSYS Mechanical模块进行谐响应分析，得到定子铁心的振动特性[11, 12]。

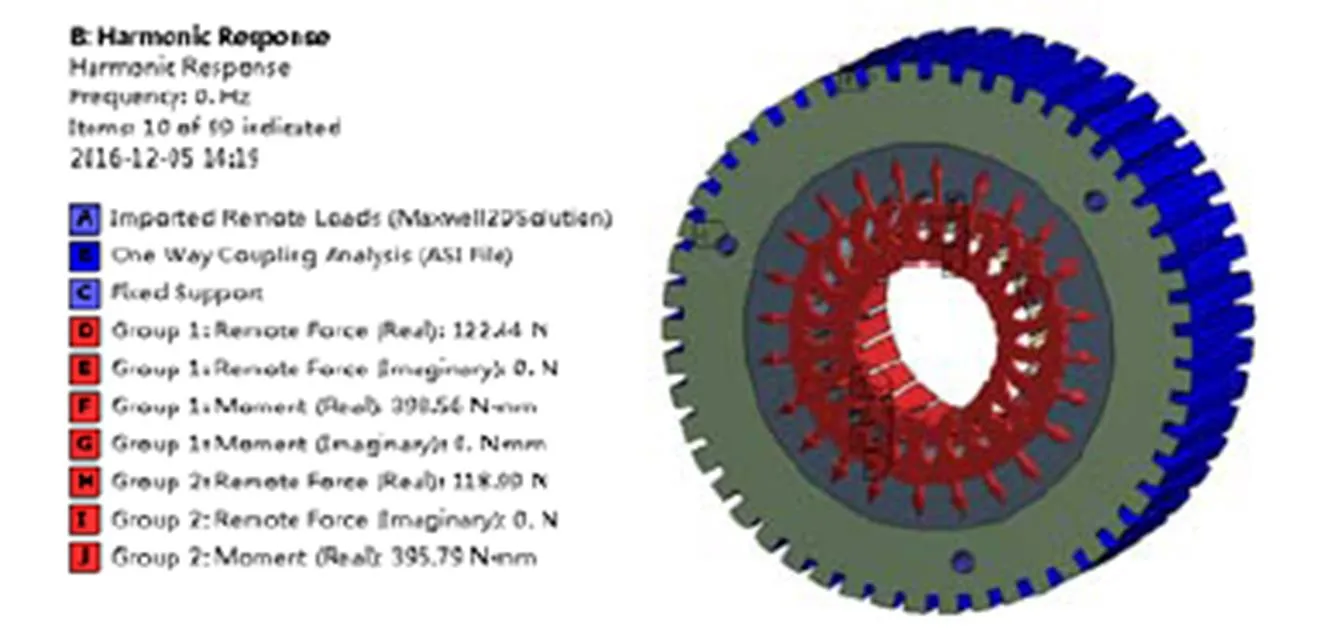
图3 电磁力的径向与切向分量作为载荷加载

两台电机的齿部变形及机壳变形如图4所示。

同时得到两台电机的机壳和齿尖的振动位移分布以及各自振动速率的幅频响应和相频响应。

从图5~图7中可以看出，在外部载荷的作用下0~10000Hz区间内，两台电机在4800Hz下振动位移和速率达到峰值，1号电机的定子铁心齿尖的振动速率幅值为0.71nm/s，定子机壳的振动速率幅值为0.39nm/s；2号电机定子铁心齿尖的振动速率幅值为0.18nm/s，定子机壳的振动速率幅值为0.11nm/s。通过以上对比分析，可以发现从振动特性上来看，2号电机的振动幅度较小，优于1号电机。那么产生的电磁噪声的情况是否还是如此，需要进一步进行声学分析[13]。

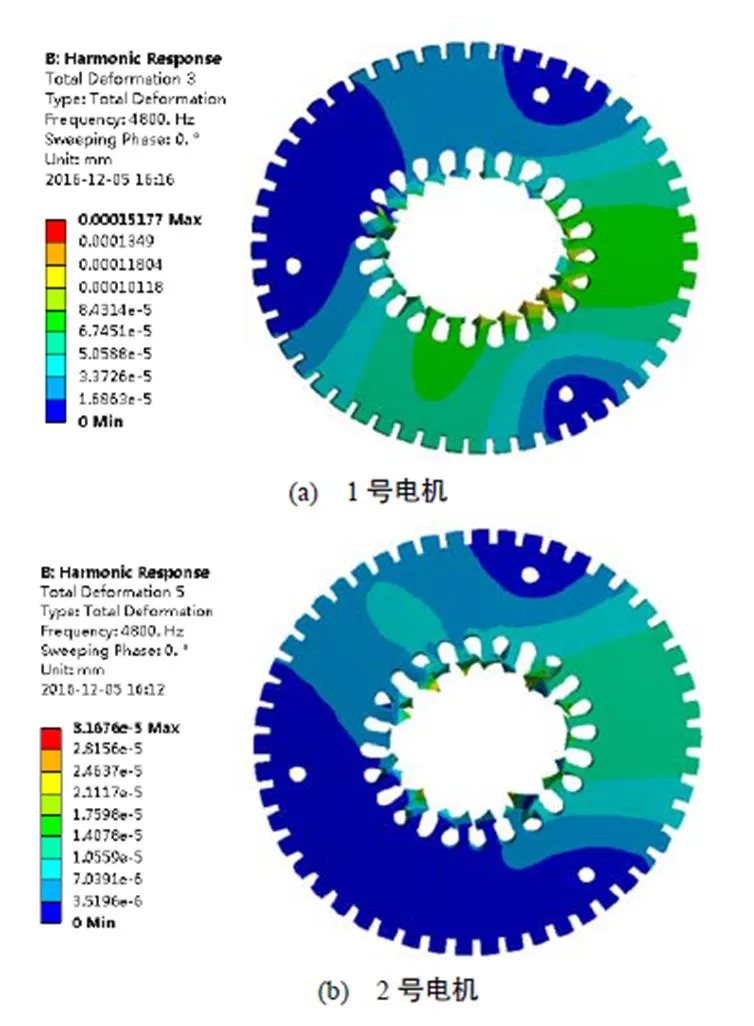
图4 1号电机和2号电机振动振型视图

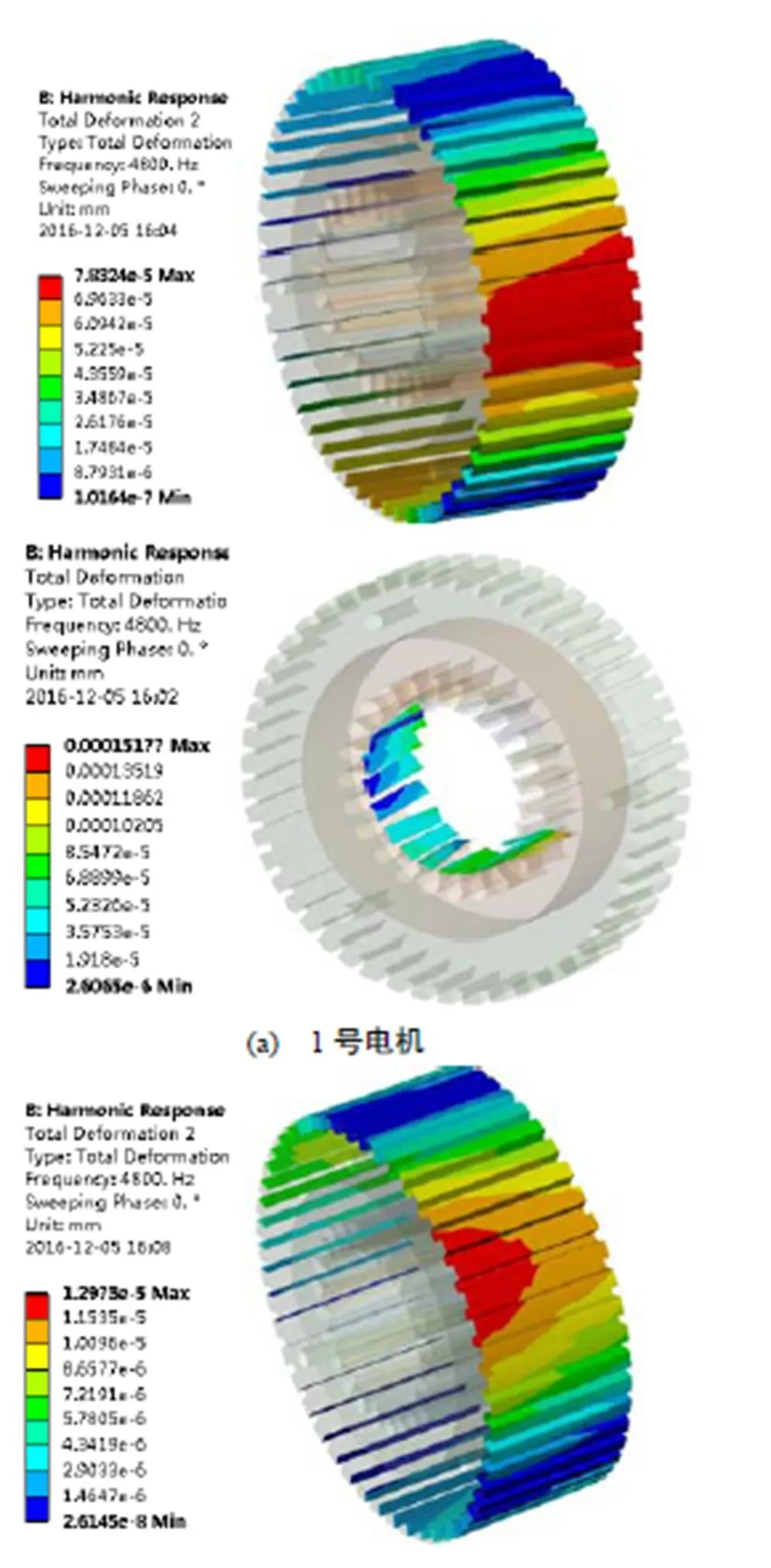
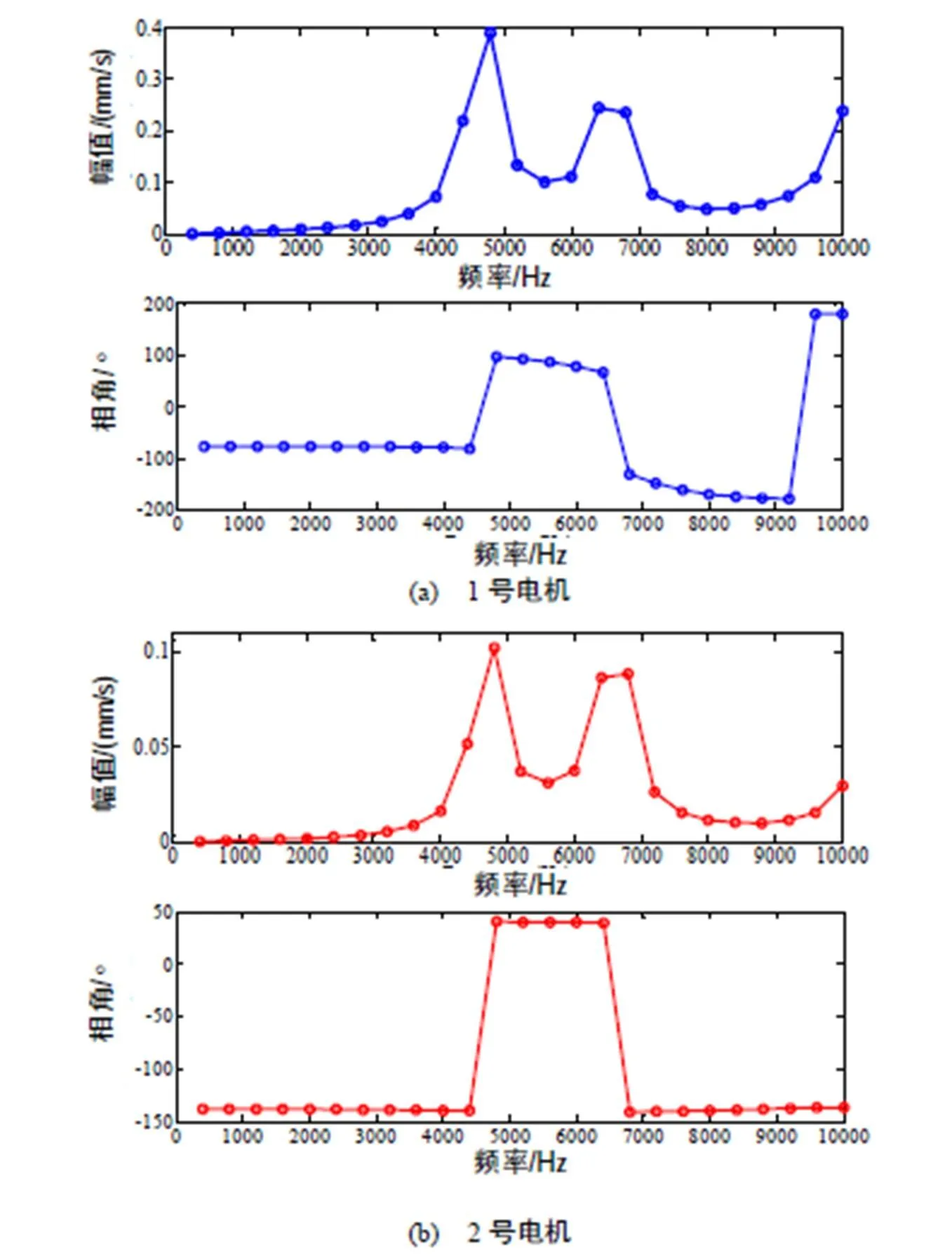
图6 1号电机和2号电机的机壳振动速率伯德图

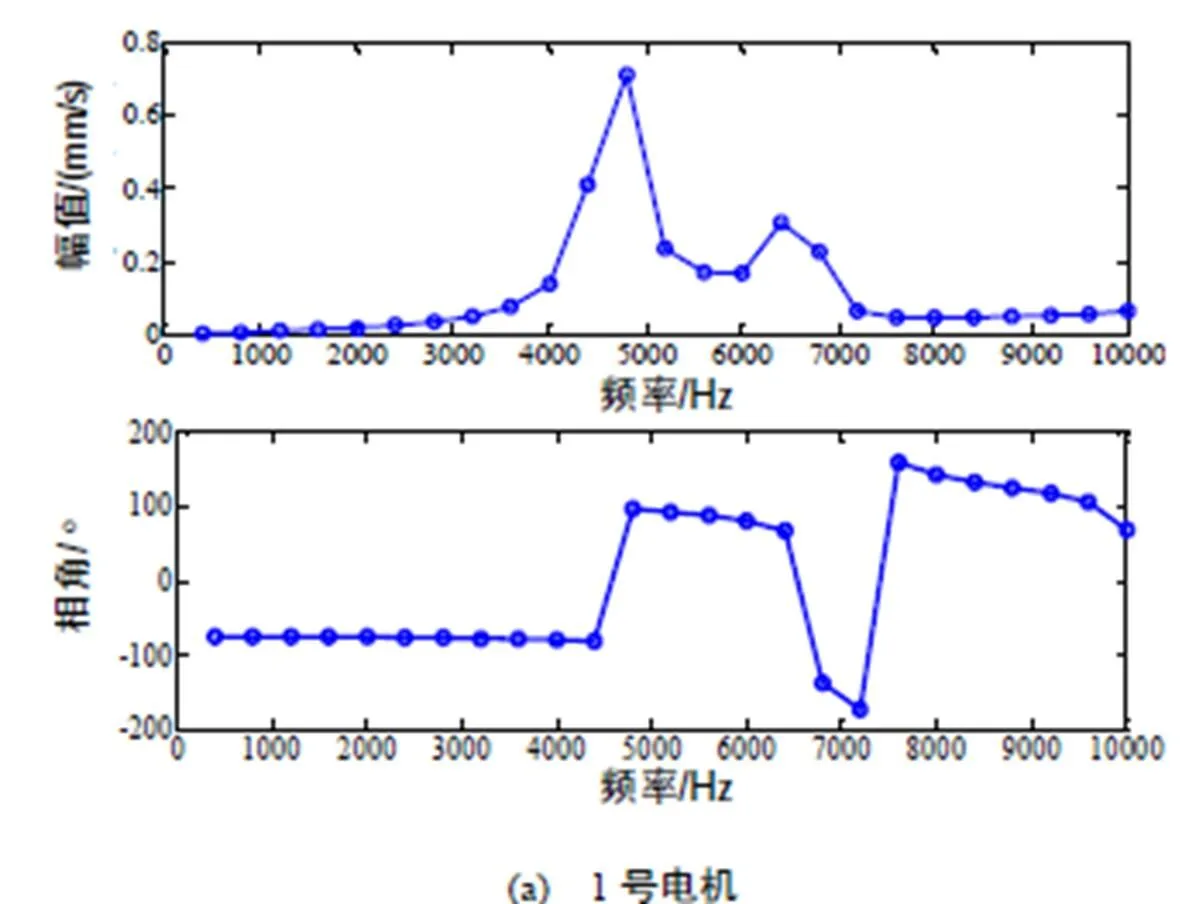
3 感应电机不同槽配合方式的声学分析

根据声学基本理论及式（7）中求解偏微分方程得到的振动速率，有

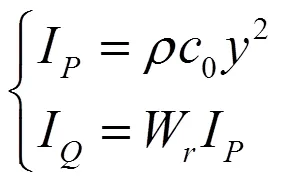
式（8）中，为空气的密度；0为声音在空气中的传播速率；W为声波相对辐射功率；I为声音按平面传播的声强；I为声音按球面传播的声强[14-15]。

将前面求解的两台电机机壳和定子铁心齿尖的振动速率作为声学分析的输入条件，利用Acoustic模块进行声学分析，如图8、图9所示。

图8 声学分析的模型及边界条件设置

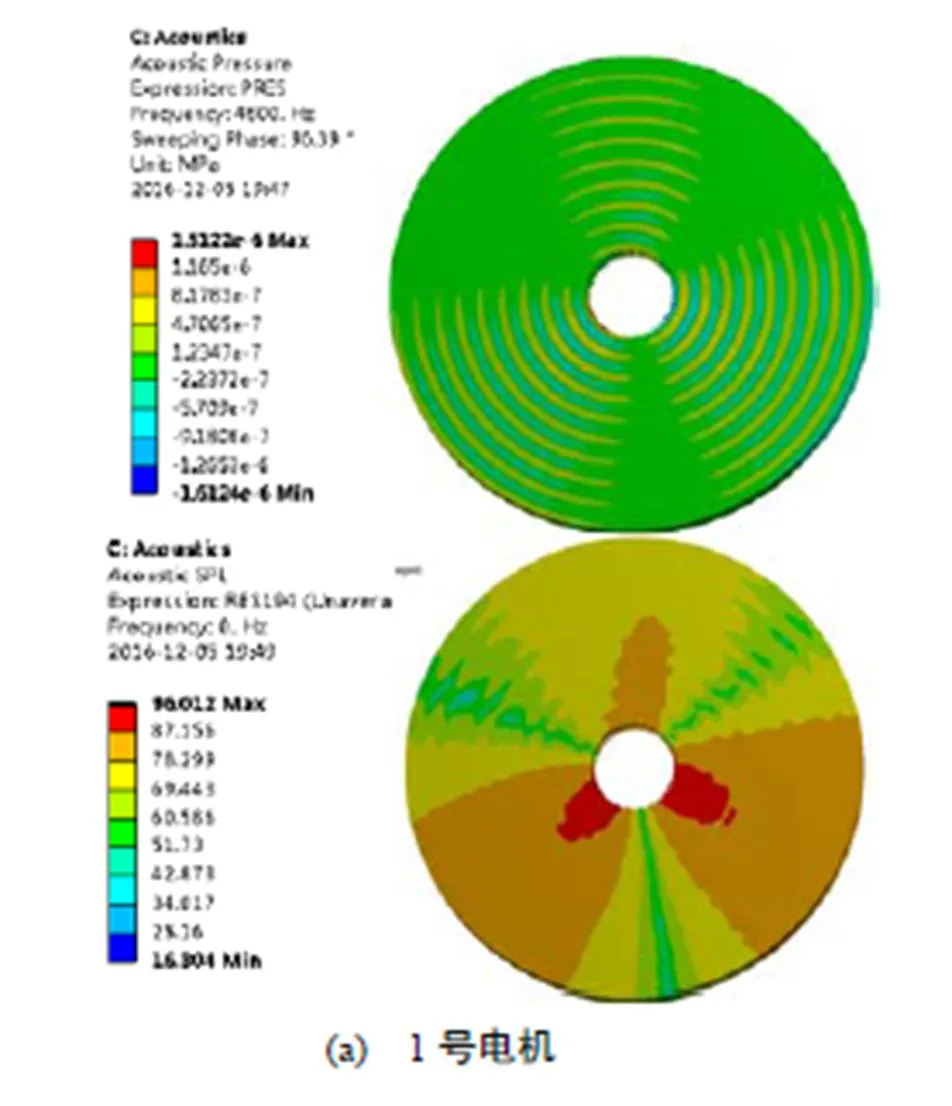
观察图9可以发现，在声场的内部，各个点的噪声分布幅值不相同；在径向各个方向上声压级(SPL)的的分布也不相同。在径向方向距机壳1m远处，1号电机的电磁噪声声压级最大为87.76dB；2号电机的电磁噪声声压级最大为73.71dB。

通过对1号电机和2号电机的试验进行实测，分别测得1号电机实测噪声为85dB，2号电机的实测噪声为74.7dB。

经过上面的计算和分析，我们确定槽配合方式为24/26的1号电机在振动和电磁噪声两个指标上均不如槽配合方式为24/31的2号电机。此结果也经过了试验的实测进行验证，可以确保仿真计算的准确性。

4 结论

本文以两台不同槽配合方式，容量为7.5kW的三相感应电机为研究对象，在对其进行槽配合力波分析的基础上，提出了一种通过多物理场的有限元耦合进行分析和研究的方式，在求解多个问题后，最终达到了对不同槽配合方式的感应电机电磁振动和噪声的完整分析。分析的结果与实测噪声验证吻合得也非常好，说明这种分析方式的准确性。最终2号电机(槽配合方式为24/31)的电磁振动和电磁噪声均比1号电机(槽配合方式24/26)要小，这为今后的感应电机设计提供了降低振动和噪声的指导。

[1] 陈永校, 等. 电机噪声的分析和控制[M]. 浙江大学出版社, 1987.

[2] 陈世坤. 电机设计[M]. 机械工业出版社, 2002.

[3] 张维, 黄坚. 综合分析槽配合与定子振动特性降低[J]. 电机与控制应用, 2013, 40(10): 1-5.

[4] 苟智德, 王靖. 汽轮发电机噪声的测试与频谱分析[J]. 大电机技术, 2009(6):27-30.

[5] 彭兵. 近极槽表贴式永磁力矩电机转矩性能研究[D]. 沈阳工业大学, 2012.

[6] 魏力, 章存建, 高从闯, 等. 溧蓄推力轴承外循环系统噪声和振动问题分析与处理[J]. 大电机技术, 2017(6):22-24.

[7] 苟智德, 富立新, 孙玉田. 贯流式发电机组的噪声分析[J]. 大电机技术, 2008(6):23-27.

[8] 黄涛, 阮江军, 张宇娇, 等. 基于多物理场耦合计算分析的多相异步电机设计平台[J]. 大电机技术, 2012(2):22-26.

[9] 鲍晓华, 王群京, 刘磊. 交流电机绕组的谐波分析与噪声计算[J]. 合肥工业大学学报(自然科学版), 2004, 27(10): 1252-1255.

[10] 朱海峰. 异步电机电磁激振力分析[D]. 浙江大学 2013.

[11] Hwang S M, Eom J B, Hwang G B, et al. Cogging torque and acoustic noise reduction in permanent magnet motors by teeth pairing[J]. Magnetics IEEE Transactions on, 2000, 36(5):3144-3146.

[12] 王强, 何海波. 多相感应推进电机振动分析研究[J]. 大电机技术, 2017(3):37-40.

[13] 崔淑梅, 于天达, 宋立伟. 基于ANSYS和SYSNOISE的电机噪声仿真分析方法[J]. 电机与控制学报, 2011, 15(9): 63-67.

[14] Ocak H, Loparo K A. Estimation of the running speed and bearing defect frequencies of an induction motor from vibration data[J]. Mechanical Systems & Signal Processing, 2004, 18(3):515-533.

[15] Chiba A, Fukao T, Rahman M A. Vibration Suppression of a Flexible Shaft With a Simplified Bearingless Induction Motor Drive[J]. IEEE Transactions on Industry Applications, 2008, 44(3):745-752.

Research on Noise Analysis Based on Multi-physics Field Coupling for Induction Motor

WANG Tao1, SUN Yutian1, WANG Qian2, BI Chunhui1, GOU Zhide1

(1. Harbin Institute of Large Electrical Machinery, Harbin 150040, China; 2. Harbin University of Science and Technology, Harbin 150080, China)

Electromagnetic vibration and noise analysis is often required for the design of induction motor. In this paper, a noise analysis and research method of induction motor based on multi-physics field coupling is proposed. The electromagnetic force of induction motor is coupled with vibration and noise by harmonic response analysis, and the electromagnetic vibration and noise of induction motor are solved and calculated.The simulation results show that the proposed method can accurately verified the experimental results very well.

induction motor; slot combination; multi-physics field coupling; harmonic response analysis; vibration; noise

TM314

A

1000-3983(2018)03-0011-04

2017-06-12

王韬（1984-），2011年毕业于湖南大学，硕士，工程师，现从事电机电磁分析研究工作。