基于油色谱状态边界值的变压器状态评估模型

朱 俊，谢荣斌

（贵州电网有限责任公司贵阳供电局，贵州贵阳 550001）

0 引言

变压器是电力系统的核心设备，对变压器进行科学有效的健康状态评估能够及时发现设备的故障或缺陷，为制定合理的状态检修策略提供依据，对保证设备乃至电力系统的安全可靠运行具有重要意义[1-2]。

分析油中溶解气体组分和含量是评估变压器的状态是应用最广泛和有效的手段之一[3-4]。经过多年的发展，国内外学者引入了多种现代评估方法，例如模糊综合评判[5]、可拓分析法[6]、支持向量机[7]和神经网络等[8]。然而多数评估方法在建模和评估过程中过分依赖于专家打分或人工干预，降低了评估结果的客观性和准确性。因此，亟待提出基于数据驱动的状态评估方法。

为解决传统变压器状态评估方法过分依赖专家经验和人工干预的不足，提出一种基于油中溶解气体状态边界值和熵权法的变压器状态评估模型。该模型基于数据驱动，首先收集多台变压器油中溶解气体含量全量历史数据，采用两参数Weibull（威布尔）分布模型获取各类气体的概率密度函数和累积分布函数；根据变压器不同状态等级下的分布概率，采用Weibull逆累积分布函数获取各气体组分的状态边界值，并构造状态隶属函数，采用熵权法计算各气体重要度。收集待评估变压器的油中溶解气体含量实时数据，并计算各类气体对设备状态的隶属度，并对各类气体的隶属度进行加权，进而确定变压器的健康状态。

1 基于状态边界值的油中溶解气体状态隶属函数

1.1 油中溶解气体含量的Weibull模型

Weibull分布模型用于描述随机变量分布规律，具有良好的适用性与灵活性，得到广泛应用[9]。通常采用两参数Weibull模型研究油中溶解气体分布规律，其概率密度函数和累积分布函数分别如式（1）、式（2）所示。

式中x— 某类油中溶解气体含量的量测值

f（x）—— 该气体含量分布的概率密度函数

F（x）—— 该气体含量的累积分布函数

α，β—— 别分为Weibull模型的尺度单数和形状参数，可通过极大似然估计方法计算得到

计算α，β的流程如下[10]：

（1）根据式（1）建立对数似然函数方程组，如式（3）所示。初始化尺度参数α0和形状参数β0，将某种气体含量的n条历史数据序列 X=[x1，x2，…，xn]带入似然函数。

（2）对似然函数中的2个待估计参数求偏导函数，当存在某一对α和β使得（4）成立时，则α和β为该气体Weibull分布函数的极大似然估计值，进而获得各气体含量的分布规律。

1.2 油中溶解气体状态边界值计算

南方电网公司2014年颁布的《35 kV～500 kV油浸式电力变压器（高抗）状态评价导则》（以下简称《状态评价导则》）将变压器健康状态按由好到坏依次分为正常、注意、异常和严重4个等级。由《状态评价导则》可知，油中溶解气体含量属于正劣化参量，表明设备状态会随着气体含量增加而劣化。下面提出的基于Weibull逆累积分布函数的油中溶解气体状态边界值计算方法，能够有效量化变压器状态与气体含量的关联关系[4]，具体如下。

（1）统计所有同型电力变压器处于正常、注意、异常和严重4 类状态的分布概率 P=[Pnorm，Patten，Pabn，Pser]。其中，Pnorm为所有变压器处于正常状态分布概率；Patten为注意状态分布概率；Pabn为异常状态分布概率；为Pser严重状态分布概率。

（2）对各状态等级的分布概率P进行一次累加，得到累积分布概率 F=[FI，FII，FIII，1]。

（3）将FI，FII和FIII依次带入各类气体的Weibull逆累积分布概率函数，如式（5）所示，分别得到3个对应的映射值XP=[xI，xII，xIII]。其中，xI为正常状态与注意状态的分界值，xII为注意状态与异常状态的分界值，xIII为异常状态与严重状态的分界值。状态边界值量化了4类状态与油中溶解气体含量的关联关系。

1.3 油中溶解气体状态隶属函数构造

隶属函数是模糊数学中最基本、最重要的概念，是描述模糊集合的特征函数，取值范围从集合{0，1}扩大到在[0，1]区间连续取值[1]。传统的隶属函数构造方法大多基于相关标准、规范或导则中规定的注意值。《状态评价导则》中规定变压器油中溶解气体各组分的注意值如表1所示。

表1 变压器油中溶解气体阈值

由表1可知，表中的数据不足以构造所有气体组分在不同状态等级的隶属函数，且变压器油中溶解气体的阈值会随着不同地区、不同设备类型而产生偏差。而通过专家经验确定的隶属函数往往带有较强的主观性，当专家经验或阈值与实际情况出现较大偏差时，会降低隶属函数的准确性与客观性。因此，通过状态边界值构造各气体组分状态隶属函数，4类状态等级的隶属函数分别如式（6）～（9）所示。

（1）正常状态隶属函数μ1（x）。

（2）注意状态隶属函数μ2（x）。

（3）异常状态隶属函数μ3（x）。

（4）严重状态隶属函数μ4（x）。

式中，s1=xI/2，s2=（xI+xII）/2，s3=（xII+xIII）/2，s4=（3xIII-xII）/2。

各状态等级隶属函数可视化图形如图1所示，每2条曲线的交点即为3个状态边界值。由图可知，随着气体含量的增加，设备劣化程度的隶属度越高。

通过状态边界值构造的隶属函数充分考虑了油中溶解气体含量与设备状态等级的关联关系，具有较好的客观性，能够反映设备状态随油中溶解气体的变化规律。

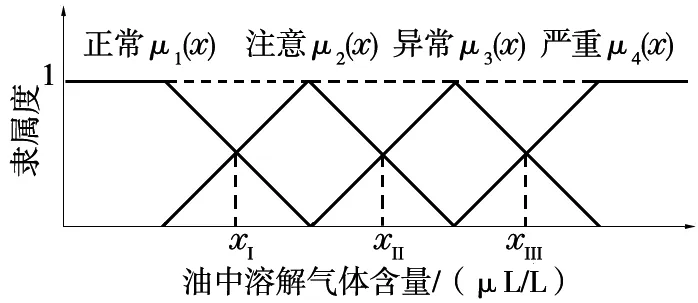
图1 油中溶解气体状态隶属函数的示意

2 特征参量的权重

层次分析法（Analytic Hierarchy Process，AHP）是计算特征参量权重的最常见方法之一[11]。但通过该方法得到的计算结果取决于专家经验，主观色彩较为明显。为避免权重计算受人工干预的影响，分析油中溶解气体数据的变化规律，提出基于熵权法的特征参量权重计算模型。

2.1 熵权法基本原理

熵权法是根据不同类型气体含量的信息熵大小来确定客观权重，若某类气体的信息熵越小，表明其得变异程度越大，在状态评估中所能起到的作用也越大，应赋予较多的权重[12]。信息熵的计算如下。

设有m种油中溶解气体分别为X1，X2，…，Xm，其中第i种气体有n组量测值Xi={xi1，xi2，…，xin}。采用最大最小法对各气体数据进行归一化，如式（10）所示，获取归一化后的量测值为Y1，Y2，…，Ym。

式中，第j组气体量测值的重要性熵值e（dj）如式（11）所示。

其中，

2.2 油中溶解气体权重计算

信息熵e（dj）用于衡量第j组气体量测值的信息有效程度，e（dj）越小则第j组量测值的有效程度越高。定义第j组气体量测值的信息效用程度为hj=1-e（dj）。

设第j组量测值的客观权重值则第i种气体的权重

基于熵权法的油中溶解气体权重计算完全基于油中溶解气体历史数据的变化特点和规律，计算过程完全由数据驱动完成，无任何人工干预，确保了计算结果的准确性和客观性。

3 基于加权模型的设备状态评估方法

根据变压器的状态等级，定义表征电力变压器状态等级的可信度指标，H=[H1，H2，H3，H4] 。其中，H1～H4分别对应正常、注意、异常和严重4个状态的可信度。

获取待评估变压器油中溶解气体的量测数据并计算各类气

根据4类状态的可信度指标计算结果，将可信度最大值对应的状态确定为该变压器的最终状态，完成设备的状态评估。

4 实例分析

4.1 基本信息

收集了某电力公司所有220 kV等级变压器3 a年内5857条油中溶解气体历史数据。共有5类气体组分，分别为氢气（H2）、甲烷（CH4）、乙烷（C2H6）、乙烯（C2H4）和乙炔（C2H2）。统计该电力公司所有220 kV变压器处于正常状态、注意状态、异常状态和严重状态的台数，经归一化计算后得到设备状态分布概率和累积分布概率（表2）。体对不同状态等级的隶属度，并根据权重对各气体的隶属度进行加权，获取待评估变压器4类状态等级的可信度计算结果，

表2 220 kV变压器状态分布概率及累积概率

4.2 油中溶解气体状态边界值计算

将油中溶解气体历史数据分别带入式（3），利用极大似然估计法计算5类气体的Weibull分布函数尺度参数α和形状参数β，结果如表3所示。以甲烷和乙烯为例，2类气体含量历史数据的频率分布和分布函数如图2所示。

表3 油中溶解气体含量Weibull分布参数计算结果

利用设备状态累积概率和Weibull逆累积分布函数分别计算7类气体的状态边界值，结果如表4所示。按照本文第1.3节方法，分别构造5类气体对4类状态等级的隶属函数。

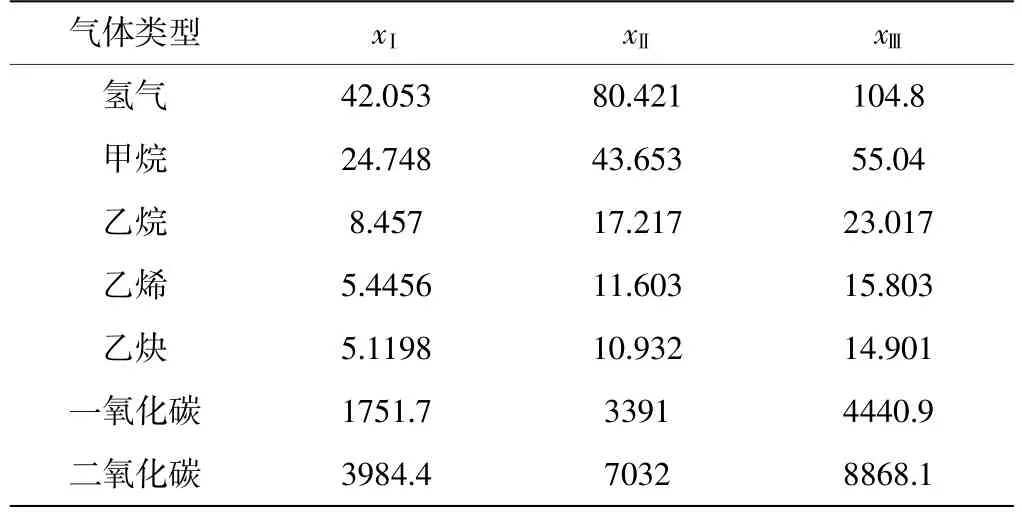
表4 油中溶解气体状态边界值计算结果 μL/L

4.3 油中溶解气体组分的权重

采用熵权法计算得到各类气体组分的权重（图3）。

由计算结果可知，乙炔的权重值较高，表明该气体反映变压器状态劣化程度的灵敏度较高。

4.4 变压器状态评估实例

4.4.1 实例1

收集1台待评估220 kV变压器（名称T1）连续的9组油中溶解气体监测数据（表5）。

将T1油中溶解气体含量监测值分别带入评估模型，计算该变压器属于4类状态的可信度（表6）。

利用南方电网公司《状态评价导则》提出的评估方法对该变压器进行状态评估，并与本文方法进行对比（表7）。

根据电网公司提供的T1设备的故障分析报告，其在第2个时间点及后续时间发生了高温过热兼放电的故障，引起变压器油分解，产生了大量气体并溶解于油中。经现场运维人员分析判断后认为，T1在第2个时间点后劣化为严重状态。

图2 甲烷和乙烯含量频率分布直方图和Weibull函数图

图3 油中溶解气体权重计算结果

根据表7中的对比分析结果可知，尽管第4和第5个时间点的油中溶解气体含量仍较高，但氢气含量出现下降趋势，总烃含量的增长率低于10%。根据《状态评价导则》的判据，此时T1的状态为注意状态，而实际上，该设备仍然存在严重的过热兼放电故障，与设备实际状态出现了偏差。

表5 T1设备油中溶解气体含量量测值 μL/L

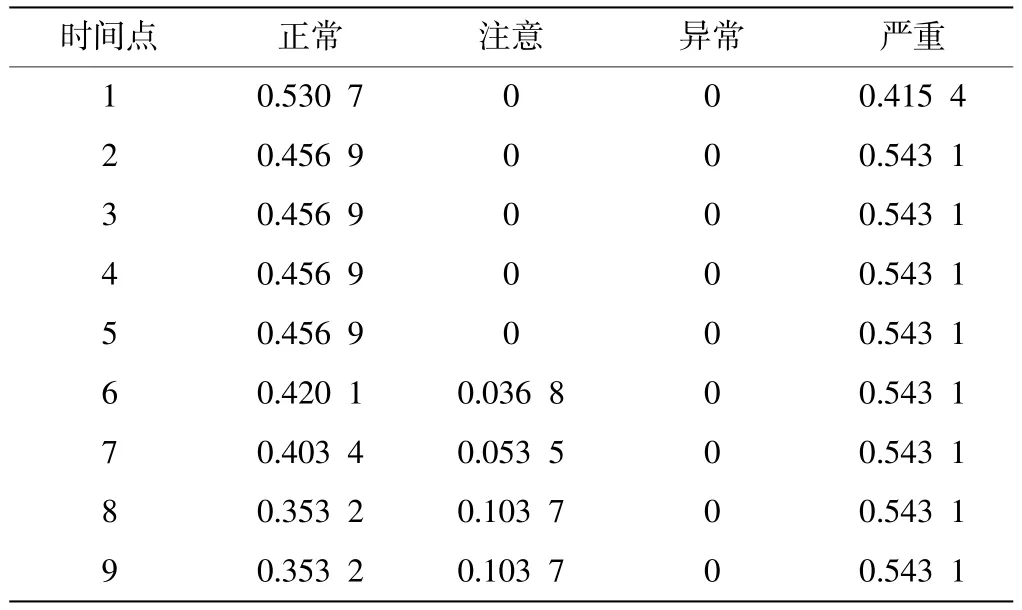
表6 T1设备状态可信度计算结果

表7 T1设备状态评价结果

本文的方法通过挖掘油中溶解气体含量与设备状态的关联关系，构造的隶属函数能够有效反应设备状态的劣化程度，评价结果的准确度得到了有效提高。

4.4.2 实例2

某台220 kV变压器（名称T2）连续的7组油中溶解气体监测数据如表8所示。

表8 T2设备气体含量量测值 μL/L

将本文方法与《导则》的评估方法进行对比（表9），发现本文方法的准确性与合理性更高，能有效反应变压器状态劣化程度。

5 结论

（1）提出一种基于油中溶解气体状态边界值和熵权法的变压器状态评估模型，通过两参数Weibull分布模型获取油中溶解气体的分布规律，并计算状态边界值，建立并量化了设备状态与油中溶解气体含量的关联关系。

表9 T2状态评价结果

（2）通过状态边界值构造的状态隶属函数，能合理反映设备状态随油中溶解气体含量的变化规律；采用熵权法计算各类气体组分的重要度，避免传统方法受主观影响的不足，计算结果与实际情况相符。

（3）实例计算表明，本文的评估方法由数据驱动完成，全过程无需依赖专家经验或人工干预，相比于传统的状态评估方法，得到的评估结果具有更好的准确性与合理性，具有良好的实用性和推广价值。

［1］王有元.基于可靠性和风险评估的电力变压器状态维修决策方法研究［D］.重庆：重庆大学，2008.

［2］何敏，徐铭铭，徐恒，等.计及可靠性的配电变压器组年度检修计划优化［J］.科学技术与工程，2017（16）：213-219.

［3］ Zheng Y，Sun C，Li J，et al.Entropy-Based Bagging for Fault Prediction ofTransformersUsing Oil-Dissolved GasData［J］.Energies，2011，4（8）：1138-1147.

［4］ HangLiu，Youyuan Wang，YiY，etal.A FailureProbability Calculation Method forPowerEquipmentBased on Multi-Characteristic Parameters［J］.Energies，2017，10（5）：1-15.

［5］廖瑞金，王谦，骆思佳，等.基于模糊综合评判的电力变压器运行状态评估模型［J］.电力系统自动化，2008，32（3）：70-75.

［6］廖瑞金，张镱议，黄飞龙，等.基于可拓分析法的电力变压器本体绝缘状态评估［J］.高电压技术，2012，38（3）：521-526.

［7］Zheng H B，Liao R J，Grzybowski S，et al.Fault diagnosis of power transformers using multi-class least square support vector machines classifiers with particle swarm optimization［J］.IET Electric Power Applications，2011（9）：691-696.

［8］阮羚，谢齐家，高胜友，等.人工神经网络和信息融合技术在变压器状态评估中的应用［J］.高电压技术，2014，40（3）：822-828.

［9］ Li Wenyuan.Risk assessment of power systems：models，methods，and applications［M］.New York：John Wiley&Sons Press，2005：281-295.

［10］钟波，刘琼荪，刘朝林.数理统计［M］.北京：高等教育出版社，2015：101-115.

［11］王毅，丁力，侯兴哲，等.基于层次分析法的加权力线窃电检测方法［J］.科学技术与工程，2017（33）：96-103.

［12］姚建华，姚多朵，蔡金明，等.基于云模型和熵权法的配电网项目融资租赁风险评估［J］.科学技术与工程，2017（18）：226-230.