针对实际轻量化设计的多材料拓扑优化

拓扑优化是进行轻量化设计的最有效的工具之一，并已在多个行业实施，以加强产品开发与创新。典型的拓扑优化需要解决的关键问题是要尽量减少系统的依从性，同时将设计空间限制在假定的体积分数上。传统单一材料的依从性问题已经扩展到包括多种材料，从而提高了设计的自由度，以便获得更好的解决方案。然而，因为依从性缺乏有用的物理意义，依从性最小化原则对实际轻量化设计具有局限性，所以从未成为工业中的设计标准。另外，传统的涉及到最小化的轻量化问题要求事先选择容积分数限制。但是，设计师往往忽略了材料之间的优化平衡问题。

在本文中，提出了一种更实用的多材料拓扑优化方法来克服这些限制。该方法在满足性能限制的同时，通过最小化总重量来寻求材料之间的优化平衡。本文还将权重最小化方法与遵从性最小化进行了比较。通过数值例子证明了权重最小化的优势，并证明了其在依从性最小化方面的益处。

举例说明，文中图7是箱体设计的模型图。该域由38,400个元素（3D网格尺寸为2.5毫米的8节点6面体元素）组成。右面是固定的，沿Z轴正方向的1000 N力位于左侧的中心。选择左侧中心（力的相同位置）的Z的正位移来设置位移约束。权重最小化方法位移限制为不大于0.01015mm，符合最高符合值的相应规定，并且通过仿真计算表明，最小权重法要比依从性最小化方法减轻质量14.9%。在实际应用中的图例见Fig.10和Fig11。

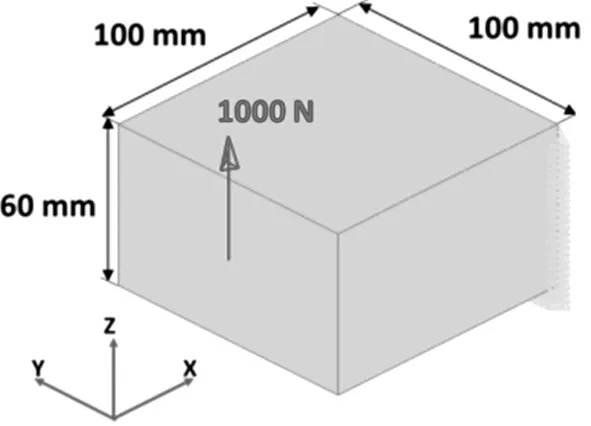
图7 箱体的设计区域

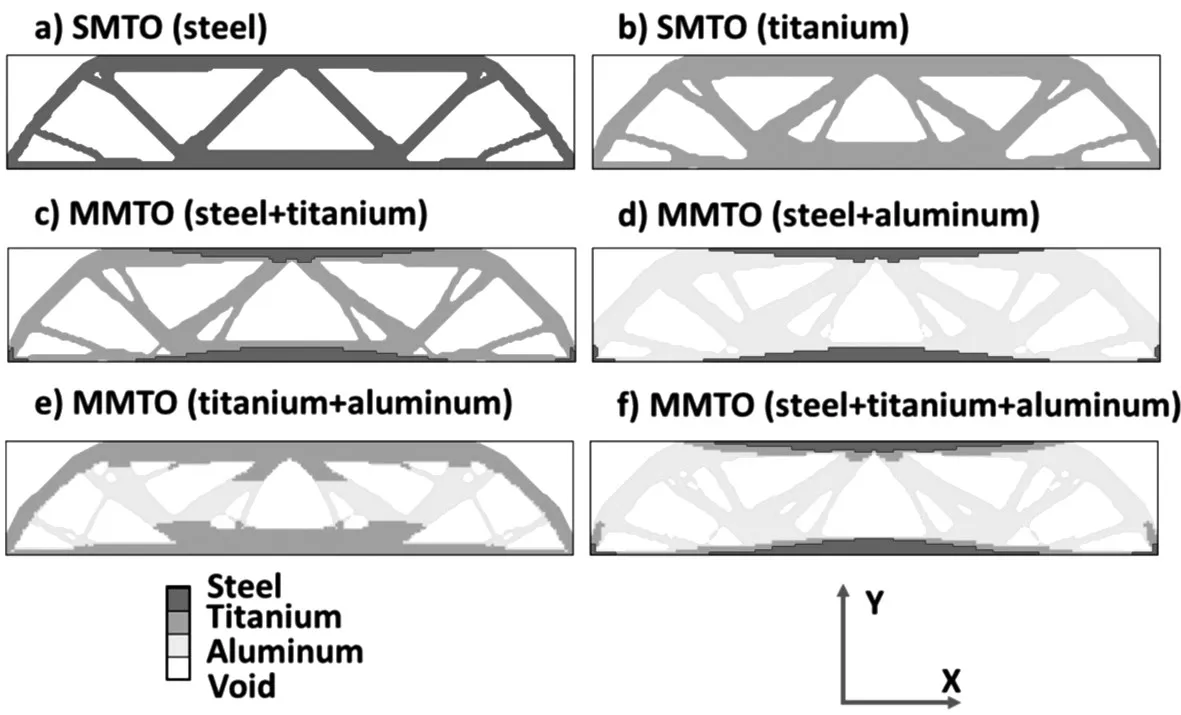
Fig.10 Material distributions when minimizing weight with UY≤0.5 mm：a SMTO(steel);b SMTO(titanium);c MMTO(steel+titanium);d MMTO(steel+aluminum);e MMTO(titanium+aluminum);f MMTO(steel+titanium+aluminum)

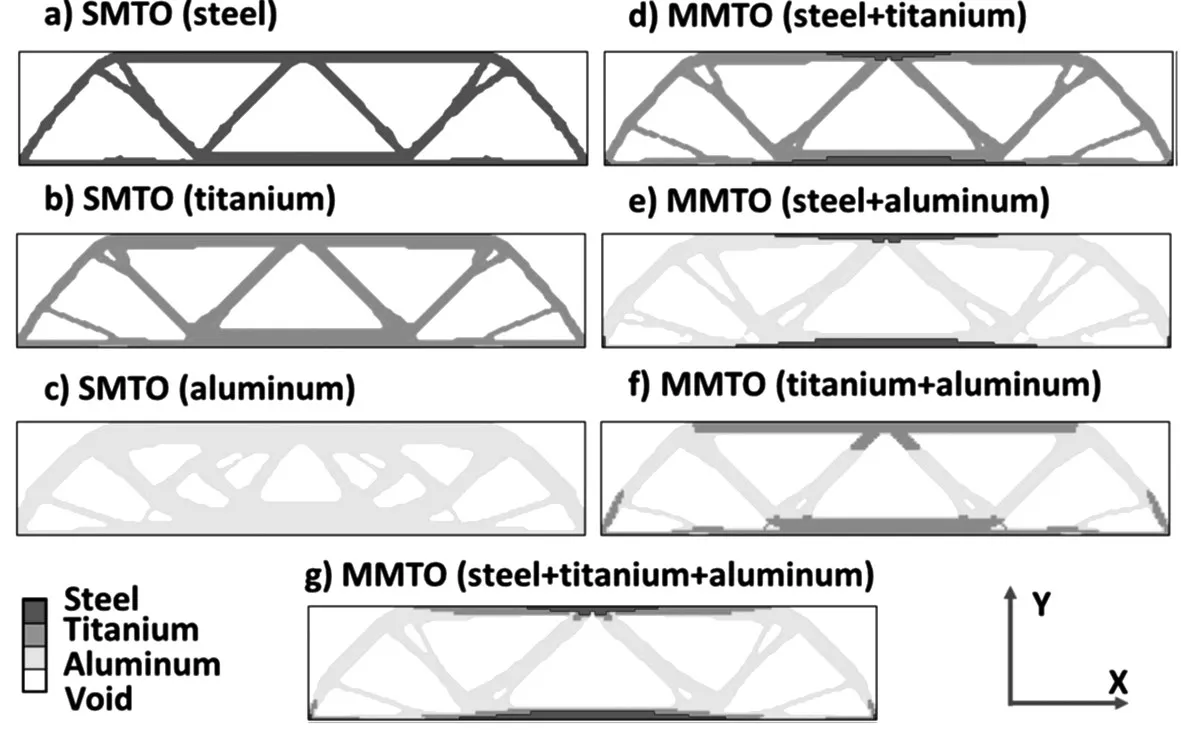
Fig.11 Material distributions when minimizing weight with UY≤0.8 mm：a SMTO(steel);b SMTO(titanium);c SMTO(aluminum);d MMTO(steel+titanium);e MMTO(steel+aluminum);f MMTO(titanium+aluminum);g MMTO(steel+titanium+aluminum)