改进的粗糙直觉模糊集

2018-06-01王金英王艳平

计算机工程与应用 2018年11期

关键词：模糊集粗糙集直觉

王金英，王艳平，齐爽

WANG Jinying,WANG Yanping,QI Shuang

辽宁工业大学理学院，辽宁锦州 121001

Science College,Liaoning University of Technology,Jinzhou,Liaoning 121001,China

1 引言

波兰科学家Pawlak于1982年首次提出了粗糙集理论[1]，几十年来，粗糙集模型不断被扩展。例如，1990年Dubois等[2]将粗糙集与模糊集相融合，提出了粗糙模糊集和模糊粗糙集的概念。2000年Boixader等[3]给出了模糊集的上下近似。2002—2003年Rizvi[4]和Cornelis等[5]基于粗糙模糊集的概念，分别定义了粗糙直觉模糊集和直觉模糊粗糙集。2008—2009年Zhou等[6-7]利用构造性方法和公理化方法，给出了直觉模糊粗糙集的上下近似算子。2010年Zhang[8]建立了区间值粗糙直觉模糊集模型，并讨论了模型的一些性质；巩增泰等[9]建立了覆盖粗糙直觉模糊集模型，并研究了其不确定性度量。2011年Thomas等[10]研究了格上的粗糙直觉模糊集。2012年Zhang[11]利用直觉模糊关系和阈值对，定义了一个新的粗糙集模型。2013年薛占熬等[12]在模糊近似空间中，结合直觉模糊等价关系，构造了新的粗糙近似算子。2014年Huang等[13]结合多粒度粗糙集和直觉模糊粗糙集，建立了直觉模糊多粒度粗糙集模型；王艳平[14]将变精度粗糙集与直觉模糊集相融合，建立了变精度粗糙直觉模糊集模型。2015年Liu等[15]采用直觉模糊集和粗糙集的思想和方法，构建了一种新的直觉模糊粗糙集模型。2016年薛占熬等[16]构建了新的覆盖粗糙直觉模糊集和新的覆盖粗糙区间值直觉模糊集两种模型。上述文献的工作都是着眼于将Pawlak粗糙集模型中的经典集合推广到其他各种模糊集合，或者将Pawlak粗糙集模型中的经典等价关系推广到模糊关系、直觉模糊关系、覆盖等。

粗糙集理论的本质思想是在一定的知识粒空间中，用一对可定义的上、下近似集来近似描述边界模糊的目标集合。随着知识粒度的减小，即人们对事物认知的加深，下近似集会逐步增大，而上近似集会逐步减小，从而使粗糙集的精度随之增大，由此可以更准确地描述目标集合。然而，在短时间内，人们对事物的认知不容易有较大的改进，那么在知识粒度不变的情况下，能否得到目标集合更好的近似集，即提高近似集的精度，并且增加近似集和目标集合之间的相似度，是一个值得深入探讨的问题。对此，2012年张清华等人[17]针对Pawlak粗糙集，利用当前知识空间中的知识粒，构建了目标集合的近似集，并分析其近似集的优越性；2015年张清华等人[18]在文献[17]的基础上，针对Pawlak粗糙模糊集，分别给出了目标集合的模糊近似集和近似精确集。尽管文献[17-18]都是在当前知识粒度不变的情况下，构建了目标集更好的近似集，但它们都是用单一的集合来近似目标集，并没有对原有的粗糙集和粗糙模糊集进行优化。为此，本文针对Pawlak近似空间中直觉模糊集的近似问题，借鉴文献[17-18]的思想，从另外的一个角度，利用直觉模糊粗糙隶属函数，构造了比现有粗糙直觉模糊集模型近似程度更好的一对上、下近似算子，从而为粗糙直觉模糊集模型在不确定性推理中的应用提供更好的理论基础。

2 相关基本知识

为讨论方便，首先给出相关的基本概念和性质。

定义1[19]设U是一非空集合，称

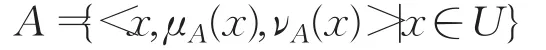
为U上的直觉模糊集，其中，∀x∈U，μA(x)∈[0,1]和vA(x)∈[0,1]分别为U中元素x属于A的隶属度和非隶属度，且满足条件0≤μA(x)+νA(x)≤1，∀x∈U 。

在下文中，记IF(U)为论域U上直觉模糊集的全体。在不引起混淆的情况下，{＜x,1,0＞|x∈U}简记为U ，{＜x,0,1＞|x∈U}简记为∅。

定义2[19]设U是一个非空经典集合，A,B∈IF(U)，规定序及运算如下：

（1）A⊆B当且仅当 μA(x)≤μB(x)且νA(x)≥νB(x)，∀x∈U；

（2）A=B 当且仅当 μA(x)=μB(x)且 νA(x)=νB(x)，∀x∈U；

（3）～A={＜x,νA(x),μA(x)＞|x∈U}。

定义3[4]设(U,R)为Pawlak近似空间，对∀A∈IF(U)，A关于(U,R)的下近似(A)和上近似(A)定义为U上的一对直觉模糊集，对∀x∈U，有

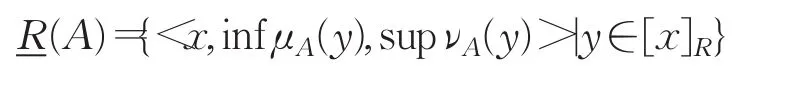
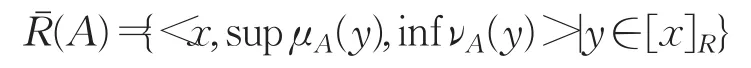
其中，[x]R={y∈U|(x,y)∈R}表示 x所在的R等价类，序对(A),(A))称为粗糙直觉模糊集。若(A)=(A)，则称A是可定义的。

定义4[20]设A∈IF(U)，定义A的基数为：

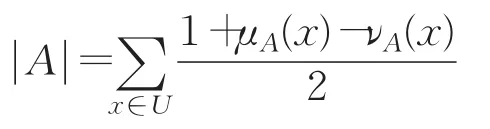
定义5[21]设(U,R)是Pawlak近似空间，对∀A∈IF(U)，则A的粗糙隶属函数R(A):IF(U)→IF(U)定义为：

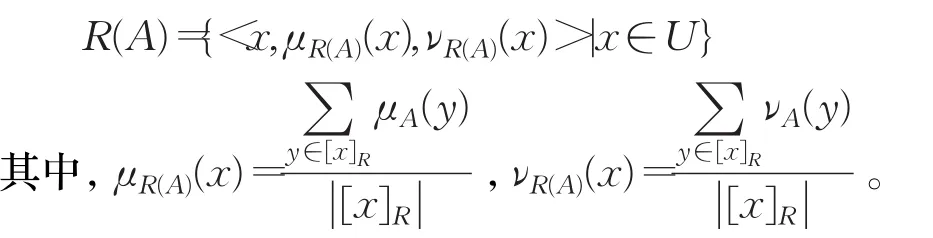
定理1[21]设(U,R)是Pawlak近似空间，直觉模糊集的粗糙隶属函数具有如下性质：

（1）∀A,B∈IF(U)，若 A⊆B，则 R(A)⊆R(B)；

（2）若 A∈IF(U)，则 R(～A)=～R(A)。

由于直觉模糊集A的粗糙隶属函数R(A)为一直觉模糊集，表示对象x隶属于直觉模糊集A的不确定程度，同一等价类中的对象其粗糙隶属度、非隶属度相等，因此有如下结论：

定理2设(U,R)为Pawlak近似空间，对 ∀A∈IF(U)，有

证明（1）因为

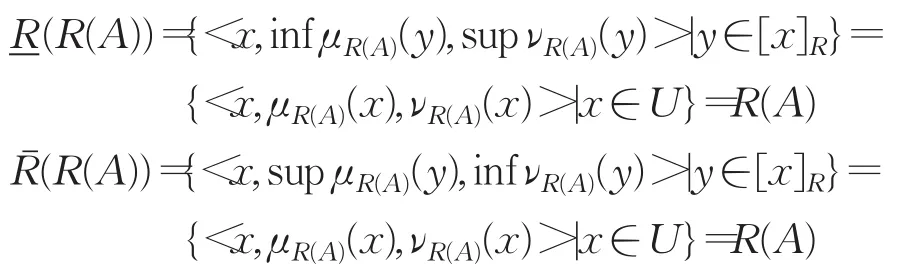
所以

（2）因为

于是有

所以

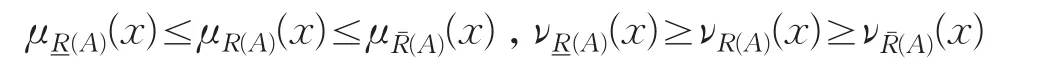
即

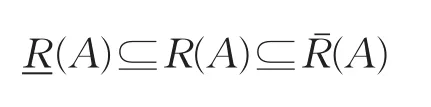
定理2表明直觉模糊集A的粗糙隶属函数R(A)为一可定义的直觉模糊集，且介于直觉模糊集A的上、下近似之间。

3 改进的粗糙直觉模糊集及其性质

在Pawlak近似空间中，直觉模糊集A的下近似算子与上近似算子均为直觉模糊集。对象x关于下近似(A)的隶属度为[x]R中所有元素隶属度的最小值，非隶属度为[x]R中所有元素非隶属度的最大值；对象x关于上近似(A)的隶属度为[x]R中所有元素隶属度的最大值，非隶属度为[x]R中所有元素非隶属度的最小值；对象x关于粗糙隶属函数R(A)的隶属度为[x]R中所有元素隶属度的平均值，非隶属度为[x]R中所有元素非隶属度的平均值。于是，用等价类中的最大值或最小值来近似目标集合有时显然不够精确，那么，能否利用[x]R中所有元素隶属度的平均值以及非隶属度的平均值来构造目标集合的近似集呢？从直观上看，这种近似应该更趋合理，为此本文建立如下的模型。

定义6设(U,R)为Pawlak近似空间，对∀A∈IF(U)，A关于(U,R)的改进的下近似(A)和上近似(A)定义为U上的一对直觉模糊集合，对∀x∈U，有

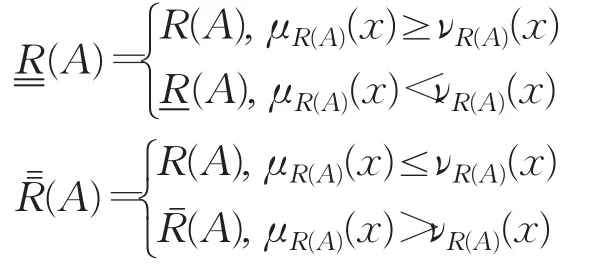
:IF(U)→IF(U)和:IF(U)→IF(U)分别称为改进的直觉模糊下近似算子和上近似算子。序对((A),(A))称为改进的粗糙直觉模糊集。若(A)=(A)，则称A是可定义的。

定理3设(U,R)为Pawlak近似空间，对∀A,B∈IF(U)，改进的下近似(A)和上近似ˉ(A)算子具有如下性质：

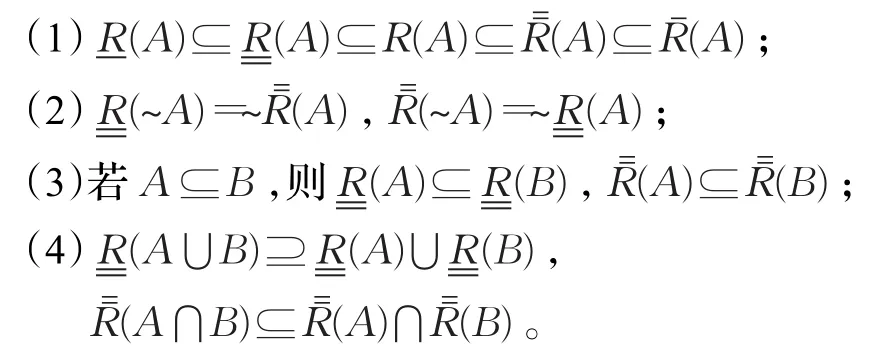
证明（1）由定理2和定义6，显然成立；

（2）因为

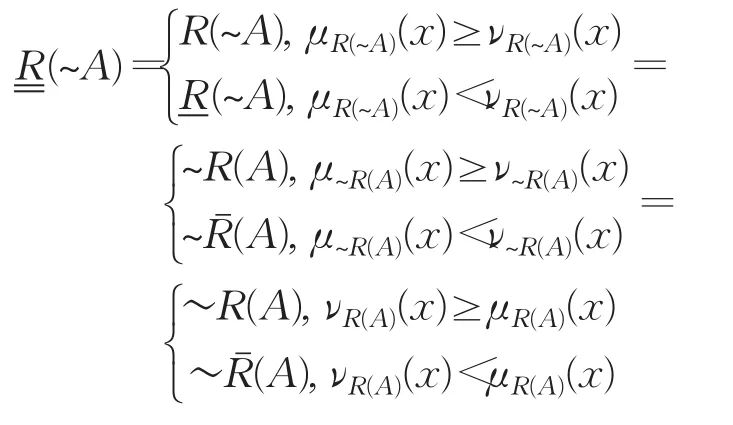
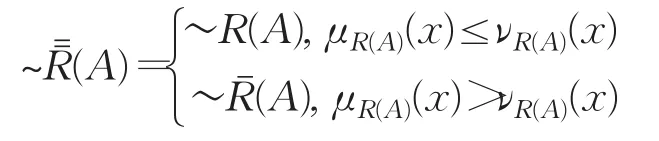
所以

同理可证：。

（3）若 A⊆B，则有

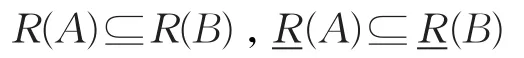
于是

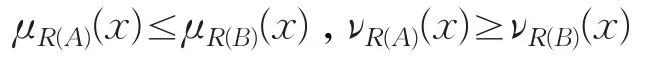
进一步可得：

又因为定义6等价于：

下面，分情况讨论：

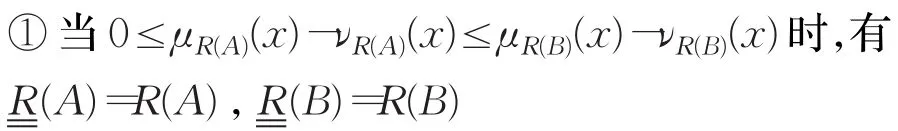
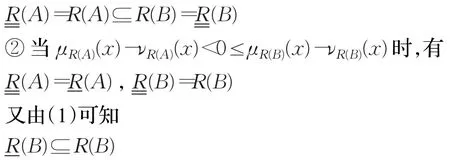
所以

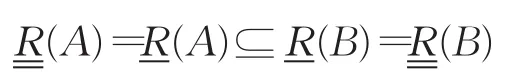
综上①②③，有。

同理可证：。

（4）由于，于是根据（3）有

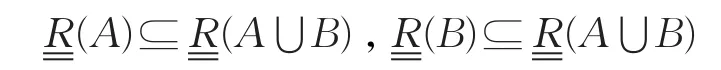
所以

同理可证：。

需要指出的是不一定成立。

定义7设(U,R)为Pawlak近似空间，对∀A∈IF(U)，定义A关于(U,R)的近似精度为：

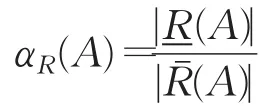
当(A)=∅ 时，约定αR(A)=1。显然，0≤αR(A)≤1。若A是可定义的，则αR(A)=1。

如果用表示改进的粗糙直觉模糊集近似集合A的近似精度，那么有下面的结论。

定理4设(U,R)为Pawlak近似空间，对 ∀A∈IF(U)，有

证明根据定理3，可知

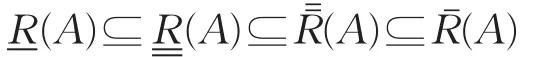
又由定义2和定义4，易知

所以

可见，用改进的粗糙直觉模糊近似算子来近似直觉模糊集A时，其近似精度会增大。

接下来，讨论改进的粗糙直觉模糊近似算子与直觉模糊集A的相似度情况。现有的直觉模糊集各种形式的相似度公式[22]已有很多类型，这里不再赘述。为了下文中定理证明以及例题计算的简便，本文采用下面的相似度计算公式。

设U={x1,x2,…,xn}，对∀A,B∈IF(U)，A与 B之间的相似度公式为：

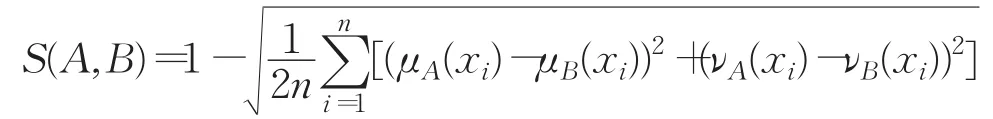
引理1[18]设x1,x2,…,xn是n个实数，令则当时，y取得最小值。

定理5设(U,R)为Pawlak近似空间，对 ∀A∈IF(U)，有

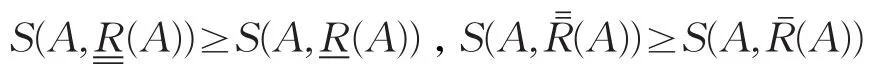
证明由相似度计算公式，得

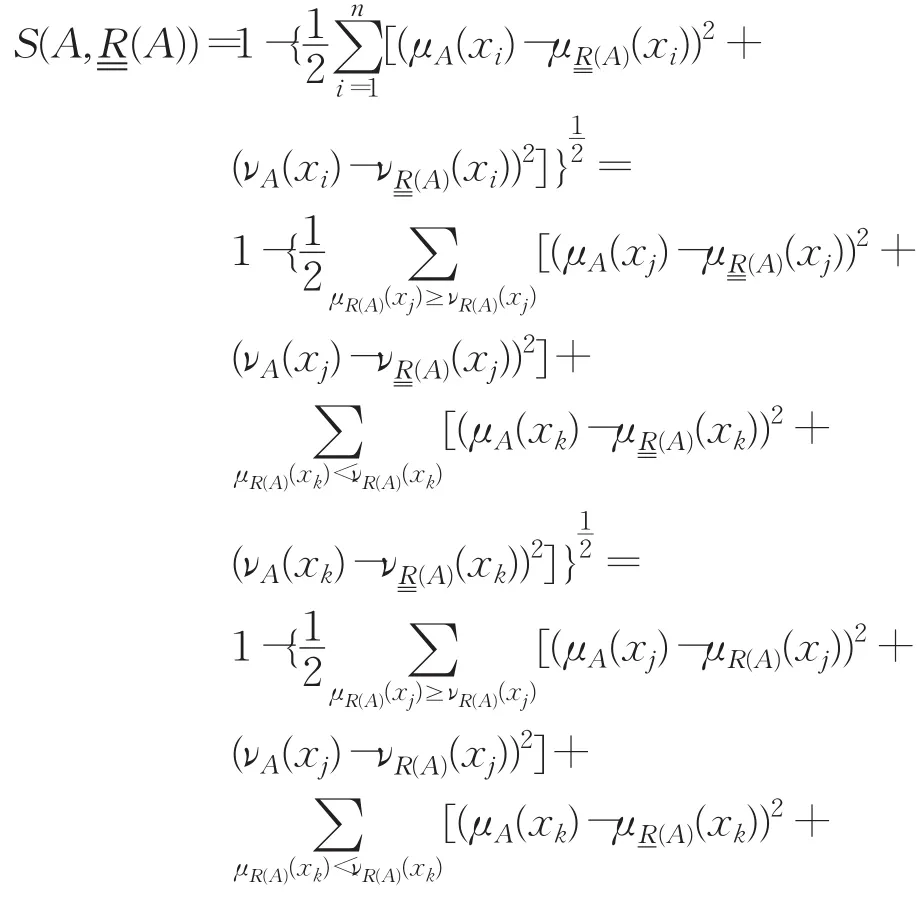
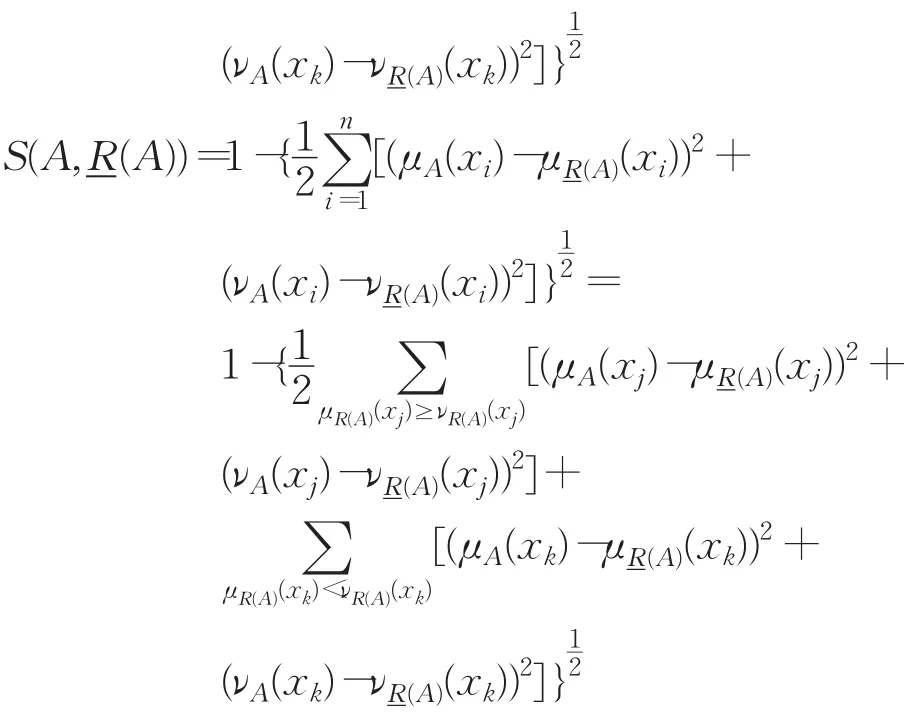
根据定义5和引理1，容易得到：

于是

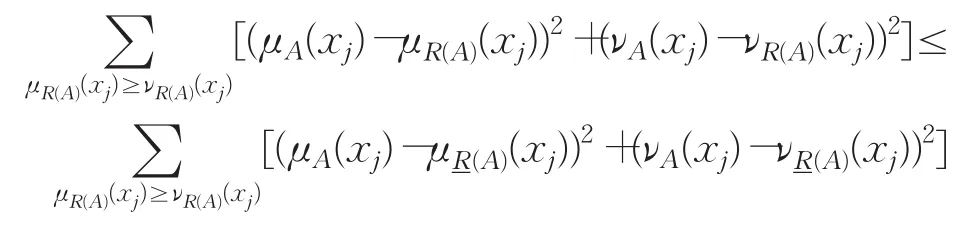
所以

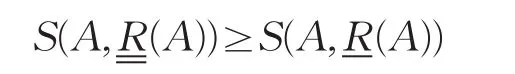
同理可证，S(A,(A))≥S(A,(A))。

定理5表明，相比文献[4]中的粗糙直觉模糊近似算子，本文构造的改进的粗糙直觉模糊近似算子与直觉模糊集A有更好的相似度，因而能够更准确地近似描述直觉模糊集A。

下面通过一个具体的算例来说明改进的粗糙直觉模糊近似算子的求法，并验证上述性质的正确性。

例1设论域U={x1,x2,…,x7}，R为U上的等价关系，U/R={X1,X2,X3}，其中X1={x1,x2,x3}，X2={x4,x5}，X3={x6,x7}。设A为U上的直觉模糊集，为简单起见，用向量形式来表示：

计算可得：

（1）比较模型改进前后直觉模糊集A的近似精度改进前：

其中，

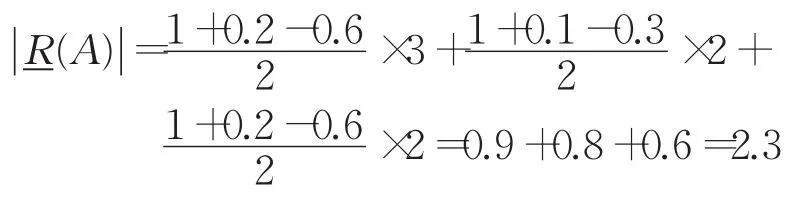
改进后：

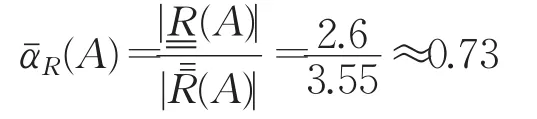
可见改进后模型的近似精度比改进前有了很大的提高。

（2）比较模型改进前后近似算子与直觉模糊集A的相似度

改进前：

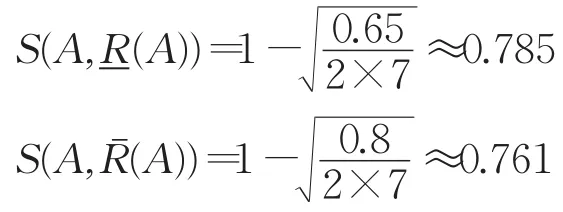
改进后：

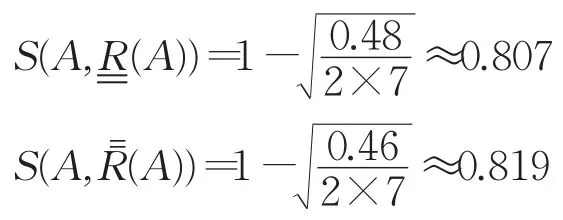
可见改进后模型的近似算子与直觉模糊目标集合的贴近度更大。

4 结束语

本文基于直觉模糊集的粗糙隶属函数构建了一个改进的粗糙直觉模糊集模型，该模型中新的上、下近似算子既依赖于同一等价类中元素对目标集合的隶属度、非隶属度的最大值和最小值，也与等价类中元素对目标集合的隶属度、非隶属度的平均值有关，因此，它能更好地接近目标集合。下一步，一方面可以考虑将本文的方法推广到其他各种扩展的粗糙模糊集模型，如粗糙区间值模糊集、粗糙区间直觉模糊集等；另一方面，可以利用本文改进的粗糙直觉模糊集模型，实现直觉模糊信息系统的属性约简，对其应用进行拓展研究。

参考文献：

[1]Pawlak Z.Rough sets[J].International Journal of Parallel Programming，1982，11（5）：341-356.

[2]Dubois D，Prade H.Rough fuzzy sets and fuzzy rough sets[J].International Journal of General System，1990，17（2/3）：191-209.

[3]Boixader D，Jacas J，Recasens J.Upper and lower approximations of fuzzy sets[J].International Journal of General System，2000，29（4）：555-568.

[4]Rizvi S，Naqvi H J，Nadeem D.Rough intuitionistic fuzzy sets[C]//Joint Conference on Information Science，2002：101-104.

[5]Cornelis C，Cock M D，Kerre E E.Intuitionistic fuzzy rough sets：At the crossroads of imperfect knowledge[J].Expert Systems，2003，20（5）：260-270.

[6]Zhou L，Wu W Z.On generalized intuitionistic fuzzy rough approximation operators[J].Information Sciences，2008，178（11）：2448-2465.

[7]Zhou L，Wu W Z，Zhang W X.On characterization of intuitionistic fuzzy rough sets based on intuitionistic fuzzy implicators[J].Information Sciences，2009，179（7）：883-898.

[8]Zhang Z.An interval-valued rough intuitionistic fuzzy set model[J].International Journal of General Systems，2010，39（2）：135-164.

[9]巩增泰，马延.覆盖粗糙直觉Fuzzy集模型[J].计算机工程与应用，2010，46（3）：42-45.

[10]Thomas K V，Nair，Latha S.Rough intuitionistic fuzzy sets in a lattice[J].Int Math Forum，2011（25/28）：1327-1335.

[11]Zhang Z M.A rough set approach to intuitionistic fuzzy soft set based decision making[J].Applied Mathematical Modelling，2012，36（10）：4605-4633.

[12]薛占熬，程惠茹，黄海松，等.模糊空间中的直觉模糊粗糙近似[J].计算机科学，2013，40（4）：221-226.

[13]Huang B，Guo C X，Zhuang Y L，et al.Intuitionistic fuzzy multi-granulation rough sets[J].Information Sciences，2014，277：299-320.

[14]王艳平.基于变精度粗糙直觉模糊集的决策规则获取[J].计算机工程与科学，2014，36（3）：541-544.

[15]Liu Y，Lin Y.Intuitionistic fuzzy rough set model based on conflict distance and applications[J].Applied Soft Computing，2015，31（2）：266-273.

[16]薛占熬，司小朦，朱泰隆，等.覆盖粗糙直觉模糊集模型的研究[J].计算机科学，2016，43（1）：44-48.

[17]张清华，王国胤，肖雨.粗糙集的近似集[J].软件学报，2012，23（7）：1745-1759.

[18]张清华，王进，王国胤.粗糙模糊集的近似表示[J].计算机学报，2015，38（7）：1484-1496.

[19]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20（1）：87-96.