交互协调强化学习下的城市交通信号配时决策
2018-06-01夏新海XIAXinhai
夏新海XIAXinhai
广州航海学院 港航管理学院,广州 510725
School of Port and Shipping Management,Guangzhou Maritime University,Guangzhou 510725,China
1 引言
目前城市路网交通拥挤问题日益突出,而作为城市道路交通管理的核心部分,城市交通信号配时决策是实现城市道路交通流有效运行的重要保障[1]。城市路网中各交叉口处的交通流是相互关联和影响的(特别是在较高饱和度交通条件下)。因此为了更有效地进行城市交通的交通信号配时决策,有必要引入协调机制。
国外强化学习在城市交通自适应交通信号配时决策中应用研究取得重要进展。文献[2-5]分别应用多目标混合多agent强化学习、基于细胞传输模型的强化学习、基于tile coding的Q-强化学习、基于节点树的多agent强化学习来进行城市路网交通协调控制,但未深入引入直接交互机制。Mannion P[6-7]提出将启发式预见性建议及并行计算融入到强化学习来进行交叉口的交通信号配时决策,但还存在计算复杂性的问题,并且强调各个交叉口之间的独立学习。虽然Arel I[8]、Medina J C[9]进行的自适应交通信号配时决策研究中分别考虑了相邻交叉口的状态、相对交通量、延误、拥挤水平等信息,但是这些方法没有包含任何外在的协调机制。Alvarez I[10]、Clempnera J B[11]利用马尔科夫决策过程为交叉口交通信号配时决策进行建模,但未融入强化学习。Darmoul S,Elkosantini S,Louati A等[12]在分层多agent系统框架下,通过与相邻交叉口直接通讯和协调,其应用免疫网络算法获取交通扰动相关知识。
国内学者也已经意识到自适应交通信号配时决策中协调机制研究的重要性,取得了可喜的成果。首艳芳、徐健闽[13]通过引入群体动力学来进行交叉口群协调控制机制研究,但未结合强化学习研究。闫飞、田福礼、史忠科[14]研究了城市区域交通信号迭代学习控制策略,但未引入协调机制。戈军、周莲英[15]提出了一种基于SARSA(λ)的实时交通信号控制模型和算法,但没有考虑相邻交叉口的关联性。Li Li[16]通过建立深度神经网络来学习强化学习的Q函数,但也未考虑与相邻交叉口的交通信号配时决策的协调。
综上所述,目前对于自适应交通信号配时决策中应用强化学习存在如下问题:
(1)城市交叉口自适应交通信号配时决策中强化学习与协调机制结合研究还不够深入。先前大部分的研究主要考虑独立强化学习,虽然少数学者考虑了两级协调,但协调机制不够深入。(2)维数灾难问题。虽然目前存在多agent强化学习方法,但遭遇维数灾难问题,需要每个agent观察整个系统的状态,这在运输网络情况下是不可行的。本文在设计城市交通信号配时决策的独立Q-强化学习算法的基础上,通过引入交互协调机制进行拓展,并通过仿真实验分析其有效性和收敛性。
2 基于独立Q-强化学习的交叉口交通信号配时决策算法
Q强化学习是Watkins于1989年提出,是强化学习算法中应用最为广泛的并最有效的一种方法,其基本原理见文献[17]。下面在Q-学习算法的基础上构建面向自适应交通信号控制的独立强化学习算法。
(1)交叉口交通状态空间S
选择信号周期C、各相位的绿灯时间gi作为状态变量,以四相位交叉口为例,其相位为{东西直行右转,东西左转,南北直行右转,南北左转},则S=(C,g1,g2,g3,g4)。
(2)交叉口信号控制动作集A
针对交叉口的交通状态,以固定配时方案为初始方案,通过调整各相位的绿灯时间,形成对应的信号控制动作集。以4个相位控制的交叉口为例,设Δgi为第i相位的绿灯时间调整量,各个相位均可采取三种动作,分别是增加绿灯时间2 s,保持不变,减少绿灯时间2 s,即 Δgi={+2 s,0 s,-2 s},则 A={(g1+Δg1,g2+Δg2,g3+Δg3,g4+Δg4)},并且A是离散的、有限的。
(3)奖惩函数r(s,a)
这里,奖惩函数采用消极回报,即行为的车均延误越大,得到的回报r(s,a)越大,则惩罚越大。根据周期时间的车均延误与周期时间的比率来建立r(s,a)。

其中rt(s,a)为在状态s下,时间步t采取行为a所获得的奖励;dtk为时间步t对应的行为集A采取行为a的周期时间车均延误;dt0为每一时间步t起始方案产生的周期时间车均延误;C0、Ck分别为变化前后的周期时长。
(4)算法流程
根据以上分析,设计算法如下:
①设置学习因子αt、折扣系数γ;
②令t=0,将所有的Q0(s0,a0)设为固定配时方案的车均延误;
③重复每一时间步;
④选取初始状态s0;
⑤根据策略,从状态s0对应的行为集A选择一个行为at+1;
⑥执行行为at+1,计算即时回报rt+1(见式(1)),转到下一状态st+1;
⑦这里以车均延误最小为目标,使得Q值最小,采用下式更新Q函数:
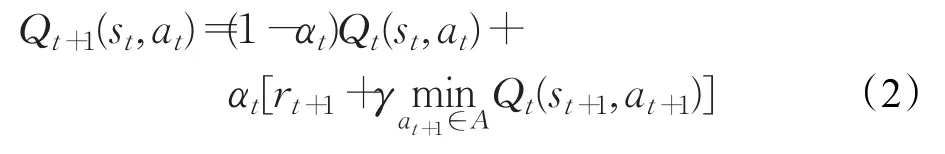
⑧ s←st+1,t←t+1;
⑨直到Q值由小变大,终止学习,否则返回③。
3 引入协调机制的强化学习算法设计
本文第2章介绍的独立强化学习算法中,交叉口交通信号控制agent在利用其局部状态和局部行动及方程(2)进行独立学习和决策时,遭遇维数灾难问题,即状态空间随着交叉口个数增加呈指数增长,因此引入直接交互机制,相邻交叉口交通信号控制agent间直接交换配时动作和状态,对独立Q-强化学习算法进行扩展,从而提高相邻交叉口间的交通信号协调配时决策的效率并增强其有效性。
3.1 算法基本思想
(1)交叉口交通信号控制agent间的交互
每个交叉口交通信号控制agent在进行本交叉口局部交通信号配时决策时均受到其他交叉口特别是相邻交叉口局部交通信号配时决策的影响,因此交叉口交通信号控制agent间需要进行状态和动作等信息的交互,交互过程见图1,此交互环境属于离散动态交互。
(2)算法基本思想
交叉口交通信号控制agenti从随机局部动作(a*0i)开始,并与相邻交叉口交通信号控制agenti交换动作和状态。对任意 j∈{1,2,…,|NBi|},交叉口交通信号控制agenti通过更新Q-值来学习同其相邻的交叉口交通信号控制agentj的相应(i,j)的最优联合动作。根据当前动作集给定相邻交叉口交通信号控制agent的动作,每一交叉口交通信号控制agent利用下一状态应当采取的动作的值来更新Q-值。
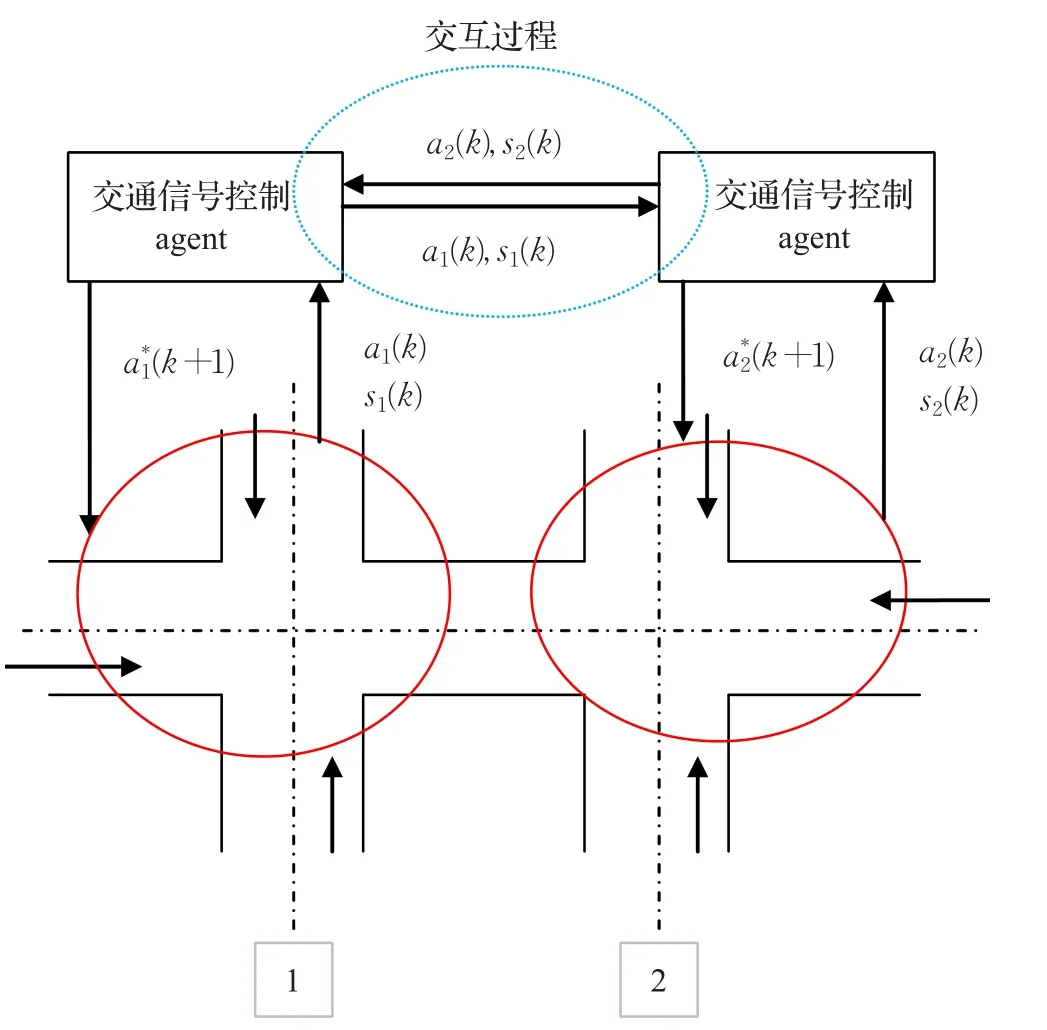
图1 交叉口交通信号控制agent间的交互过程
3.2 算法流程设计
根据上述思路构建的基于交互协调机制的强化学习算法流程如下:
(1)初始化:对每一交叉口交通信号控制agenti,i∈{1,2,…,N},及每一相邻交叉口 j∈{1,2,…,|NBi|},初始化,,,。
(2)对于每一时间步k,及每一交叉口交通信号控制agenti,i∈{1,2,…,N},广播当前动作。
(3)每一相邻交叉口 j∈{1,2,…,|NBi|},接收动作。
(4)观察,及。
(5)更新αk。

(6)更新Qi,j。

(7)更新并确定。
3.3 交互协调学习中动作选择
交互协调学习中动作的选择是关键。在基于交互协调的强化学习方法中,交叉口交通信号控制agenti通过与相邻交叉口交通信号控制agentj进行直接交换策略来产生下一个配时动作。交叉口交通信号控制agenti根据当前配时动作以及接收到的相邻交叉口交通信号控制agentj的动作计算其相对于相邻交叉口交通信号控制agentj的效用Uc和最优反应策略的效用Ubr,见式(3)和式(4)。差值 (Ubr-Uc)表示一个收益值,这里称为交互点Gain(i),见式(5)。交互点值反映交叉口交通信号控制agent间决定是否进行交互的阈值。

交叉口交通信号控制agenti将其交互点值告知给相邻交叉口交通信号控制agentj并接收到它们的交互点值。如果当前周期交叉口交通信号控制agenti的交互点值比所有从相邻交叉口交通信号控制agentj获得的交互点值都大,即当Gain(i)≥Gain(j),交叉口交通信号控制agenti就会将此配时动作更新为最优配时动作,见式(6),并告知给相邻交叉口交通信号控制agentj。

此过程一直重复直到所有相邻的交叉口交通信号控制agentj改变它们的配时动作为止。
4 仿真分析
4.1 问题描述
以图2路网为例来进行交叉口间交通信号协调配时决策分析。车道长度452 m,东西为主干道方向,自由车流速度50 km/h,南北向车流量qNS1=qSN1=705辆/h,qNS2=qSN2=903辆/h,qNS3=qSN3=902辆/h。

图2 分析用到的路网
对于基于独立Q-强化学习的交通信号协调控制算法,其每一交叉口交通信号控制agent采用Q-学习算法时,仅仅考虑其局部状态和动作,其需要协调的车流方向由控制中心决定,仅当位于干道的检测器检测到一个确定的交通模式才予以改变。以东西主干道为例,如果协调的车流为东向西方向车流(qEW),图2中东向西方向车道上行驶的车辆期望不停车地通过干道。如果协调的车流为西向东车流(qWE),图2中西向东车道上行驶的车辆获得优先权。为了简单起见,设东向西方向的车流量更大,控制中心最初决定这个方向的所有交通信号的协调。
4.2 方法有效性分析
4.2.1 车道车流密度分析
采用车道平均车流密度作为性能指标,其代表车辆的空间密集度。为了减少学习的状态空间,降低计算复杂度,对于车流密度按定性信息处理,不同交通状态对应的交通密度值的定性描述见表1。

表1 不同交通状态对应的交通密度值的定性描述
对三种交通情况进行分析,以东西方向为例,对于情况(1),一个方向的车流量明显大于另一个方向的车流量;对于情况(2),两个方向车流量均为中等大小;对于情况(3),两个方向车流量中等偏低,仿真分析结果见表2。
(1)东向西车流量(qEW)明显比西向东车流量(qWE)大。qEW=1 088辆/h,qWE=170辆/h,其车流量分别对应于表1中的密度区间D-4和D-2。
基于独立强化学习的交通信号控制方法运行的效果比较好,这是因为一个方向的车流量总比反方向的车流量大,从而使得基于交互协调机制的强化学习方法的优势没有得到充分发挥。将利用独立强化学习和基于协调机制的强化学习方法分别获得的东向西车道的密度区间进行比较,可以发现独立强化学习得到的密度区间与基于协调机制的强化学习的相同,或者低一个区间。例如,对于车道3→2的平均密度,在独立强化学习下是D-4,而在基于协调机制的强化学习下是D-5。
由于西向东的交通流流量qWE低,无论是独立强化学习还是基于协调机制的强化学习都不可能对协调的性能进行干扰。这是因为在仿真运行过程中,西向东的交通流从来没有要求优先权。
(2)东西两个方向车流量均为中等大小。qEW=1 088辆/h,qWE=332辆/h,两者都对应于表1中密度区间D-4。
由于两个方向都表现为交通拥挤,交叉口交通信号控制agent必须处理两个方向的交通协调的竞争。因此,此时基于协调机制的强化学习更能体现其自适应性。然而,基于协调机制的强化学习具有优越性不仅仅是因为它能够处理交叉口的局部交通变化,而且还因为在这种方法下干道的总的通行能力增加了。
就东向西车道而言,基于协调机制的强化学习的性能与独立强化学习的性能相比,两者相同或者前者要更优一个密度区间。当比较西向东方向的车道时,基于协调机制的强化学习的交通信号控制性能明显地优于独立强化学习的交通信号控制方法。这是因为独立强化学习方法未能给予交叉口的水平方向优先权,也就意味着协调的解除。在另一方面,基于协调机制的强化学习允许交叉口交通信号控制agent在必要情况下改变协调。
(3)相反两个方向都具有中等偏低车流量。东向西的车流密度对应区间为D-1,而西向东车流密度对应区间为D-2。虽然两个方向的车流量仅仅是微小变化,但基于协调机制的强化学习的也比独立强化学习运行效果更好。这是由于车流在两个方向相对偏小,交通流量相对自由地经过干道,并且交叉口局部交通状态变化不大。
综合上述(1)~(3)三种情况可以看到,当一个方向车流量明显高于相反方向车流量的稳定情况下,由于很少或者没有交通冲突发生,独立强化学习方法运行效果更好(见情况(1))。然而,当相反两个方向的车流量几乎相等的情景下,相对于基于协调机制的强化学习来说独立强化学习方法运行效果较差。这是因为,基于协调机制的强化学习方法具有一定的自适应能力,能够在很短时间内处理交叉口局部交通变化,并且能允许交叉口交通信号控制agent在一定条件下改变协调。因此当比较干道的每一个车道的平均密度时,基于协调机制的强化学习的交通信号控制被证明更加有效。

表2 独立强化学习和基于协调机制的强化学习车道车流密度分析
4.2.2 路网系统的性能分析
以整个路网系统的车均延误和总等待排队长度为性能指标,在上述车流情况(2)下,即东西两个方向都获得一个中等大小车流量时候,比较固定配时、最大排队优先[18]、独立强化学习、协调强化学习四种方法的性能,仿真运行结果见图3及图4。其中固定配时东西主干道绿灯时间设置为70 s,支线方向绿灯时间设置为40 s。总的来说车均延误、总等待排队长度均小于其他三种算法。经过近1 000次迭代运行后,其他三种算法性能明显下降,于是容易产生交通拥挤问题。此仿真结果表明基于协调机制的强化学习算法由于考虑相邻交叉口的信号交互,能有效解决城市交通拥挤问题。

图3 路网系统车均延误

图4 路网总等待排队长度
4.3 收敛性分析
收敛性分析能对算法的可靠性进行评价。图5给出了仿真过程中,三个交叉口的交通信号控制agent的交互点Gain值的变化。由于路径定义的车流量不同,路网中三个交叉口交通信号控制agent的交互点Gain的行为是不同的。随着仿真的运行,交互点值的曲线出现一些波动,这是由每一交叉口交通信号控制agent的决策过程决定的。当交叉口交通信号控制agent间决定合作时,交互点值减少;但当决定不合作时,交互点值增加。总的来说,运行2 000步后,交互点值趋向稳定。

图5 交互点值随时间变化曲线
对基于协调的强化学习算法和独立强化学习进行2 000次运行后,表3给出基于协调的强化学习算法和独立强化学习在两个方向(东向西和西向东方向)都获得一个大致相同车流量情况下的计算时间和收敛速度。相对于独立强化学习方法,基于协调的强化学习算法始终加快收敛速度。每一交叉口交通信号控制agent进行独立学习时,每一个交通信号控制agent面临着一个运动目标学习问题,即此交通信号控制agent的最优策略的变化受到其他交通信号控制agent的策略的影响。交通需求水平越高,由于交叉口交通信号控制agent之间进行直接交互,基于协调的强化学习算法收敛加速性能越好。通过表3可以看出基于独立的强化学习方法收敛速度更慢,需要更多的计算时间。

表3 计算时间和收敛速度
5 结语
设计了交叉口交通信号进行控制的独立强化学习算法。在此基础上,通过引入交互协调机制对独立强化学习算法进行拓展,即相邻交叉口交通信号控制agent间直接交换状态、配时动作和交互点值,解决独立强化学习算法存在的维数灾难问题。通过仿真实验分析,当相反两个方向的车流量几乎相等时,基于交互协调的强化学习的控制效果明显优于独立强化学习算法,协调更有效,并且基于交互协调机制的强化学习算法能加快收敛速度。交通需求水平越高,基于协调机制的强化学习算法收敛加速性能越好。本研究为将多agent强化学习应用于干线和区域自适应交通信号控制奠定理论基础。
参考文献:
[1]Han Ke,Sun Yuqi,Liu Hongcheng,et al.A bi-level model of dynamic traffic signal control with continuum approximation[J].Transportation Research Part C:Emerging Technologies,2015,55:409-431.
[2]Khamis M A,Gomaa W.Adaptive multi-objective reinforcement learning with hybrid exploration for traffic signal control based on cooperative multi-agent framework[J].Engineering Applications of Artificial Intelligence,2014,29:134-151.
[3]Chanloha P,Chinrungrueng J,Usaha W,et al.Traffic signal control with cell transmission model using reinforcement learning for total delay minimisation[J].International Journal of Computers Communications&Control,2015,10(5):627-642.
[4]Abdoos M,Mozayani N,Bazzan A L C.Hierarchical control of traffic signals using Q-learning with tile coding[J].Applied Intelligence,2014,40(2):201-213.
[5]Zhu F,Aziz H M A,Qian X,et al.A junction-tree based learning algorithm to optimize network wide traffic control:A coordinated multi-agentframework[J].Transportation Research Part C Emerging Technologies,2015,1:1-33.
[6]Mannion P,Duggan J,Howley E.Learning traffic signal control with advice[C]//Proceedings of the Adaptive and Learning Agents Workshop,2015.
[7]Mannion P,Duggan J,Howley E.Parallel reinforcement learning for traffic signal control[J].Procedia Computer Science,2015:956-961.
[8]Arel I,Liu C,Urbanik T,et al.Reinforcement learningbased multi-agent system for network traffic signal control[J].IET Intelligent Transport Systems,2010,4(2):128-135.
[9]Medina J C,Benekohal R F.Q-learning and approximate dynamic programming for traffic control—A case study for an oversaturated network[C]//Transportation Research Board 91st Annual Meeting.Washington DC:Transportation Research Board,2012.
[10]Alvarez I,Poznyak A,Malo A.Urban traffic control problem a game theory approach[C]//Proceedings of the 47th IEEE Conference on Decision and Control,2008:2168-2172.
[11]Clempnera J B,Poznyakb A S.Modeling the multi-traffic signal-control synchronization:A Markov chains game theory approach[J].Engineering Applications of Artificial Intelligence,2015,43(8):147-156.
[12]Darmoul S,Elkosantini S,Louati A,et al.Multi-agent immune networks to control interrupted flow at signalized intersections[J].Transportation Research Part C Emerging Technologies,2017,82:290-313.
[13]首艳芳,徐建闽.基于群体动力学的协调控制子区划分[J].华南理工大学学报:自然科学版,2013(4):77-82.
[14]闫飞,田福礼,史忠科.城市区域交通信号迭代学习控制策略[J].控制与决策,2015(5):71-75.
[15]戈军,周莲英.基于SARSA(λ)的实时交通信号控制模型[J].计算机工程与应用,2015,51(24):244-248.
[16]Li Li,Lv Yisheng,Wang Feiyue.Traffic signal timing via deep reinforcement learning[J].IEEE/CAA Journal of Automatica Sinica,2016,3(3):247-254.
[17]Watkins C.Q-learning[J].Machine Learning,1992,8(3):279-292.
[18]Wunderlich R,Liu C,Elhanany I,et al.A novel signalscheduling algorithm with quality-of-service provisioning for an isolated intersection[J].IEEE Transactions on Intelligent Transportation Systems,2008,9(3):536-547.
