深沟球轴承轴向承载能力控制技术研究

刘卫萍

(四川信息职业技术学院，四川 广元 628040)

深沟球轴承轴向承载能力控制是提高转子轴承承载能力的关键技术。深沟球轴承轴控制系统是一个非线性的强耦合系统，在进行承载控制时容易受到转子轴承的机械转矩和惯性力矩等因素的影响，导致影响控制输出的多元性耦合因素较多，轴承承载能力控制的稳定性不好，影响整个机械部件的平稳性和承载能力，甚至会导致深沟球轴承轴断裂，因此，研究深沟球轴承轴的承载能力优化控制方法，在提高深沟球轴承轴的机械强度、优化深沟球轴承轴的加工设计等方面都具有很高的应用价值，相关的控制优化技术在汽车制造和飞机制造等领域具有广阔的开发前景[1]。

对深沟球轴承轴向承载能力的控制多采用模糊PI控制方法，由于神经元的不确定扰动[2-4]，导致该种方法对轴承的力学控制存在时延，不利于对轴承的轴向状态进行控制，输出结果的误差较大。因此，优化设计轴承轴向承载能力控制方法成为目前学者的研究重点。其中，文献[5]中提出一种基于凸优化理论和稳态误差修正的承载力学控制方法，但在承载力的传输控制中，随着基线漂移的增大容易出现失真，导致无法稳态控制轴承轴向承载力，输出误差大。为此，笔者提出一种基于力矩反馈补偿调节的深沟球轴承轴向承载能力控制技术，利用反馈补偿对轴承轴向承载能力控制方法进行优化，以降低不确定因素对控制的干扰，得到较好的深沟球轴承轴向承载能力控制性能。

1 深沟球轴承轴向承载能力控制对象

本文研究的深沟球轴承轴向承载能力控制对象模型分为力学控制模型、运动学控制模型以及执行器控制模型等。分析深沟球轴承轴向承载能力控制的优化问题是提高轴承承载能力的重要手段。本文采用稳态误差补偿方法进行承载力学反馈调节补偿控制[6]，以提高力学承载控制的稳定性。深沟球轴承轴向承载能力控制的模型如图1所示。

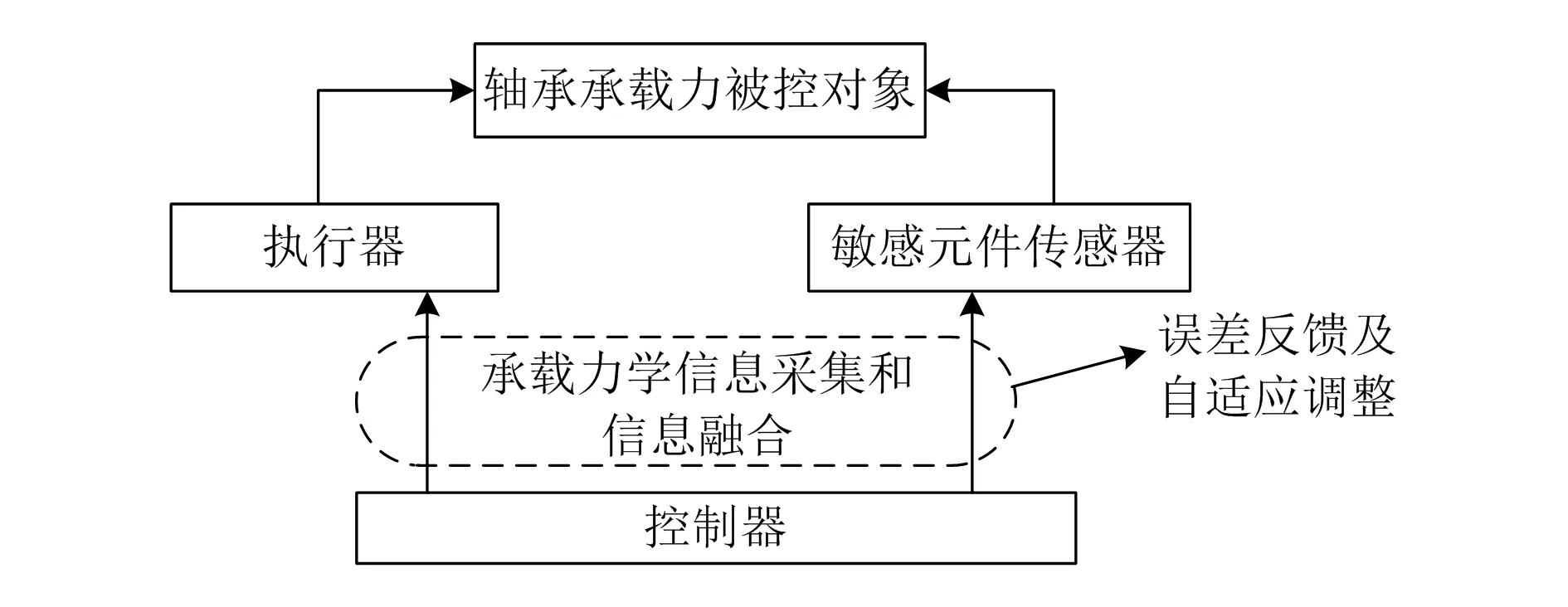
图1 深沟球轴承轴向承载能力控制的模型

根据图1进行控制对象和控制约束参量分析，为了简化分析，给出如下假设：1)深沟球轴承为类似于七自由度多维转矩的控制力学部件，深沟球轴承的外形关于体坐标系x1oy1平面对称，轴承在受力过程中的惯性力矩和转矩具有非线性和耦合性，活动部件对轴承的力学控制具有扰动性特征[7]；2)深沟球轴承运动链记为{A0,A1}，作用力矩呈均匀正态分布；3)深沟球轴承的外形结构为一个简化的刚体结构模型，承载力学控制满足经验分布[8-12]。

2 轴承轴向承载力学分析

在上面对深沟球轴承轴向承载能力控制对象的描述基础上，考虑控制器存在的不确定时延和不确定扰动，进行承载力学分析[13]，得到的轴承承载力的控制状态方程可表示为：

(1)

(2)

式中：A,B,C,D,F1,F2为惯性力矩矩阵；x(k+1),z(k)为轴承表面承载力状态方程组；w(k)∈Rn，表示有限的扰动误差，即w(k)∈L2(0,∞)，其中变量n为正整数；ΔA1,ΔB1为惯性误差系数矩阵；K为反馈增益矩阵；τk为控制时间节点；G为翻倾力矩；A1,B1为截面抗弯承载矩阵;F为轴向承载力学分布矩阵。

G∈Rr×l,A1∈Rl×p,B1∈Rl×q，均为轴承补偿控制的实对称矩阵，对所有满足FTF≤I的轴向承载力学分布矩阵F，有Y+HFE+ETFTHT<0成立，其中I为闭环控制矩阵，Y为单轮控制矩阵，H为对角控制向量，E为控制能耗。承载力学的转矩变量r,l为正整数。记

(3)

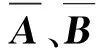
当稳态误差矩阵Q，S，M及常数ε大于0时，深沟球轴承轴向承载能力控制的参数反演积分控制的Lyapunove函数满足：

(4)

在满足控制律稳定性Lyapunove泛函的条件下[14]，轴向承载能力控制具有H∞性能，说明控制器具有稳定性。

3 控制算法优化

在已构建的轴承轴向承载控制力学约束参量模型的基础上，进行控制算法改进设计。本文提出一种基于力矩反馈补偿调节的深沟球轴承轴向承载能力控制技术，采用Lyapunove反演积分方法进行稳态误差修正[15]。当误差修正的权系数w(k)≠0时，得到控制增益和反馈调节系数矩阵分别为：

(5)

Φ2=[xT(k)xT(k-τk)KTwT(k)]

(6)

(7)

式中：ΔVk为控制增益量；Φ2为扰动力矩矩阵；Π2为反馈调节系数矩阵。

采用闭环控制方法进行承载能力调节系数融合处理，考虑到是用由N个深沟球轴承姿态采集敏感元件组成的传感阵列进行参数测量，得到输出的控制律稳定的充分条件：

(8)

假设承载力的参考门限初始值为0，引入误差反演调节函数：

(9)

其中γ>0为常数，得到惯性权重w(k)≠0，而且w(k)∈L2[0,∞)，则轴承承载力控制的分布函数为：

(10)

在承载能力控制律的后置单元中引入积分项进行力矩反馈补偿，运用连续EKF(扩展卡尔曼滤波器)来进行承载力的最优分配函数估计，当满足式(11)时，得到一个期望的深沟球轴承步态跟踪信号。式中：U为承载力分配系数矩阵。

(11)

(12)

当不等式U<0成立时，所设计的深沟球轴承步态跟踪控制器满足Lyapunove稳定性原理，此时承载力分配系数矩阵可简化为：

(13)

此时，控制器的误差融合参数{δxk(0)}k≥0收敛于0，从而实现了对轴承轴向承载力的优化控制，提高了轴承轴向承载控制的稳定性。

4 仿真测试

1)实验1。

分析图2和图3可知，x1初始值为0.9，x2初始值为-1.0，在时间为4s时，x1,x2均稳定在0。由此可以看出,轴承的承载能力和控制能力较强，表明本文方法在进行位置参数调节控制中的优越性，其输出结果误差较低，对承载力的反馈调节能力较好，控制精度较高。

2)实验2。

本次实验在MATLAB7.1平台中完成，Win-dows7为本次实验的操作系统。为了验证深沟球轴承轴向承载能力，需要对深沟球轴承轴向承载能力判定系统进行测试，分别采用本文方法和文献[5]方法进行判定性能测试，记录多次试验两种不同方法的判定时间，对比两种不同方法的判定性能，对比结果如图4所示。

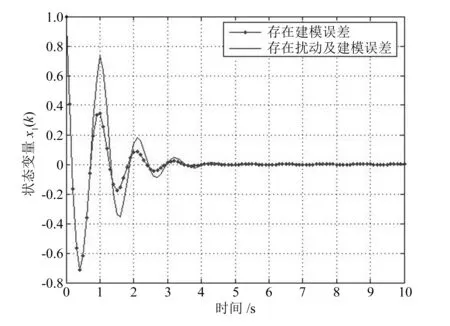
图2 深沟球轴承的承载力状态变量x1响应曲线

图3 深沟球轴承的承载力状态变量x2响应曲线

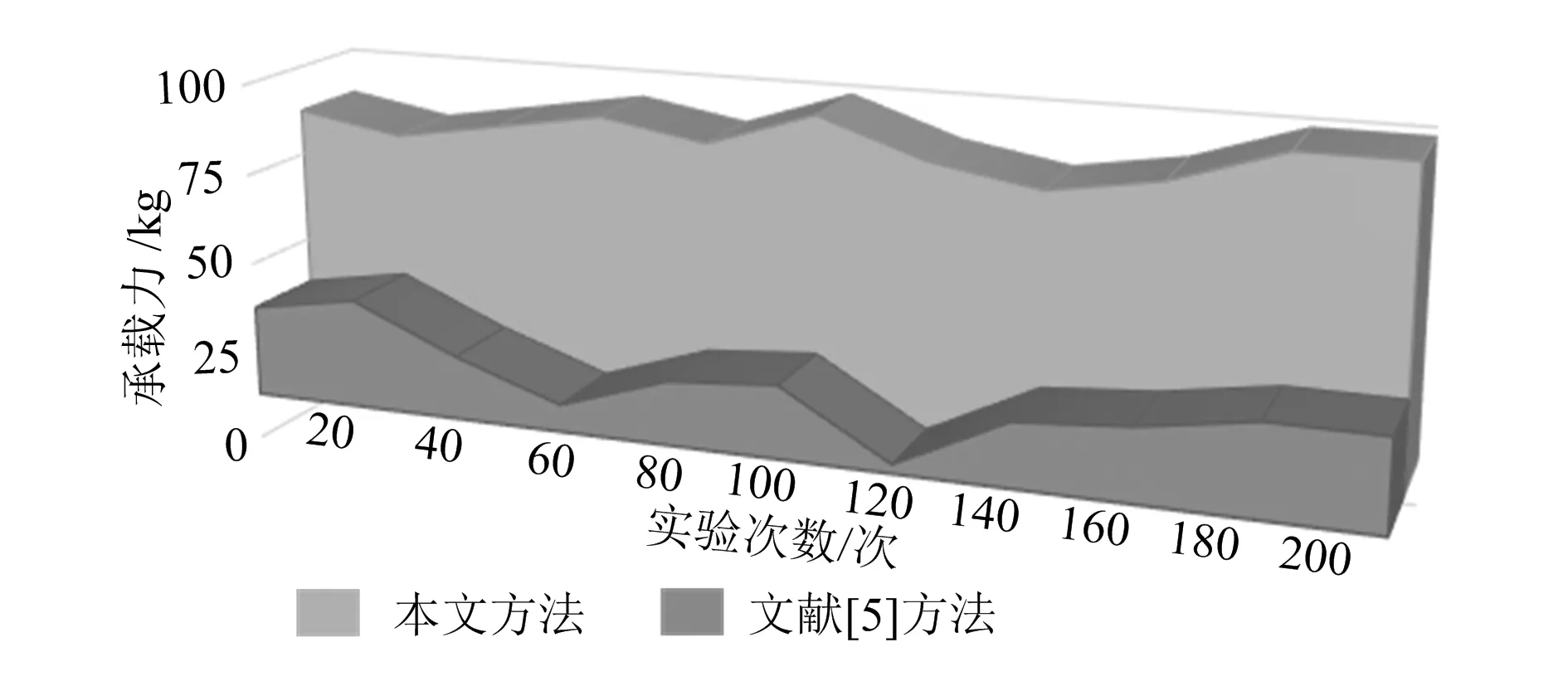
图4 深沟球轴承的承载力对比图

观察图4可知，文献[5]方法承载力较弱，承载力最高为50kg，最低为15kg；而本文方法最高承载力可达到100kg，最低为85kg，说明采用本文方法的深沟球轴承的承载能力整体较好。对比文献[5]中的方法和本文方法的测试结果，本文方法设计的深沟球轴承的承载能力大幅度增强，充分说明采用本文方法的深沟球轴承的其承载力更强，验证了本文方法的承载能力。同时，随着实验次数的增加，本文所提方法对深沟球轴承轴向承载力控制较为稳定，表明所提方法的控制稳定性较高。

5 结束语

本文提出的基于力矩反馈补偿调节的深沟球轴承轴向承载能力控制技术，在提高深沟球轴承轴的机械强度方面具有很好的性能，为稳定、准确控制轴承轴向承载力提供了一种新的方法。但目前的研究工作仅通过简单的实例对比来分析所提方法的准确性与稳定性，若要真正实现其实践价值，还需在后续研究中进一步完善承载力力学参数约束条件、修正承载力稳态测量误差，使其具有更高的应用价值。

参考文献：

[1] 任朝晖，谢吉祥，周世华，等.斜齿轮-转子-轴承弯扭轴耦合振动特性分析[J].机械工程学报,2015,51(15):75-89.

[2] PATCHARAMANEEPAKRON P, ARMOUR S, DOUFEXI A. Coordinated beamforming schemes based on modified signal-to- leakage-plus-noise ratio precoding designs[J]. IET Communications, 2015, 9(4): 558-567.

[3] 叶华聪.深沟球轴承轴向承载能力的MATLAB数值分析[J].机械制造与自动化,2017,12(6):149-151.

[4] LIU H, DING Z G, FAN P Z, et al. Precoding design for interference suppression in multi-cell multi-user networks [J]. IET Communications, 2014, 8(9): 1534-1540.

[5] 单外平，曾雪琼.基于深度信念网络的信号重构与轴承故障识别[J].电子设计工程,2016(4):67-71.

[6] 樊文刚，叶佩青.复杂曲面五轴端铣加工刀具轨迹规划研究进展[J].机械工程学报,2015,51(15):168-182.

[7] 王三秀，俞立，徐建明，等.机械臂自适应鲁棒轨迹跟踪控制[J].控制工程,2015,22(2):241-244.

[8] 杜学丹，蔡莹皓，鲁涛，等.一种基于深度学习的机械臂抓取方法[J].机器人,2017,39(6):820-828,837.

[9] 杨明，郝亮，徐殿国.基于自适应陷波滤波器的在线机械谐振抑制[J].哈尔滨工业大学学报,2014,46(4):63-69.

[10] STANKOVIC M S,JOHANSSON K H,STIPANOVIC D M. Distributed seeking of Nash equilibria with applications to mobile sensor networks[J].IEEE Transaction on Automatic Control,2012,57(4):904-919.

[11] FRIHAUF P,KRSTIC M,BASAR T. Nash equilibrium seeking in noncooperative games[J].IEEE Transaction on Automatic Control,2012,57(5):1192-1207.

[12] HESAMZADEH M R,BIGGAR D R. Computation of extremal-Nash equilibria in a single-stage MILP[J].IEEE Transaction on Power System,2012,27(3):1706-1707.

[13] 罗洁思,于德介,彭富强.齿轮箱故障振动信号的阶比多尺度形态学解调[J]．机械工程学报,2010,46(11):114-120,128.

[14] 杨兴明,余忠宇.两轮移动倒立摆的开关切换模糊极点配置控制器设计[J].电路与系统学报,2012,17(4):58-62.

[15] 熊柯,夏智勋,郭振云.倾斜转弯高超声飞行器滚动通道的自适应全局积分滑模控制[J].国防科技大学学报,2012,34(2):114-118.