圆渐开线涡旋盘啮合模态分析

刘 涛，翟凤晨，肖 伊

(兰州理工大学机电工程学院，甘肃 兰州 730050)

涡旋压缩机是一种新型的容积式压缩机，虽然它的设计理念早已经被提出，但因为制造工艺上的限制，近些年才得到飞速发展。涡旋压缩机兼具高效、小体积、低噪声的特点。作为新一代的压缩机，它的结构相对简单，运行也相对平稳，在空调制冷、动力工程及交通运输领域有着相当广泛的应用[1]。目前许多学者在其动力学性能上的研究已取得了大量理论成果。如有学者在综合考虑惯性力、气体力、温度场3个关键物理量的前提下，研究了三者共同作用下涡旋盘整体的应力变形分布情况，从而得出了涡旋盘最大应力变形发生的部位[2]。有关曲轴轴承受到的径向载荷力、径向间隙和气体产生的颠覆力矩问题，部分学者也对其进行了深入的分析，并解决了部分摩擦学与动力学的耦合问题[3]。以上多以有限元方法为基础进行动力学分析，且分析对象大多是单个涡旋盘而不是两个啮合的涡旋盘。

在实际的工况中，动涡旋盘、静涡旋盘在正常工作中始终保持啮合状态，而目前对涡旋压缩机动涡旋盘、静涡旋盘啮合后的整体分析却不多[4]。只有对啮合在一起的涡旋盘进行分析，才能更接近工况，得到的相应结论才能更好地指导实践。

1 模型的建立

1.1 弹簧-质量块模型

如图1(a)所示，首先建立最简单的动涡旋盘、静涡旋盘的弹簧-质量块模型。图中m1a为静涡旋盘的质量，m2a为动涡旋盘的质量。此模型没有考虑到啮合面的质量对振动的影响，只简单地分割出了动涡旋盘、静涡旋盘的质量，所以与实际工况相比，此模型有较大的模型误差。

图1(b)的模型是对图1(a)模型的改进，此模型考虑到了啮合面的整体质量。图中m1b为静涡旋盘的质量，m2b为啮合面的总质量，m3b为动涡旋盘的质量。

图1(c)所示模型中进一步分割了质量参量。图中m1c为静涡旋盘质量，m2c为静涡旋盘上啮合面的质量，m3c为动涡旋盘上啮合面的质量，m4c为动涡旋盘的质量。

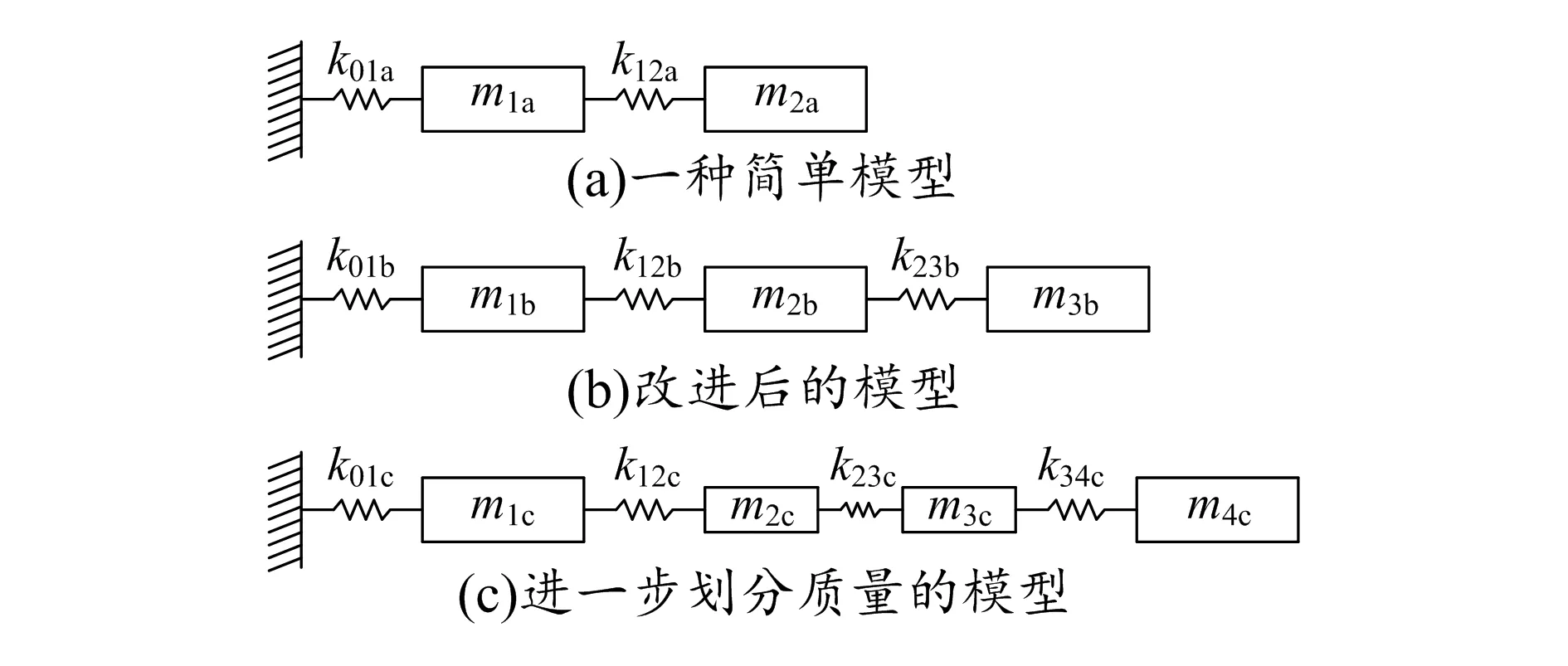
图1 几种弹簧-质量块系统模型

此时系统的数学模型为：

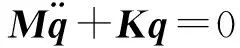
(1)

1.2 三维实体模型

弹簧-质量块模型为ANSYS Workbench有限元分析提供了相应的理论基础。由于弹簧-质量块模型中的各物理参量需要用实验测定，遂采用软件模拟仿真的方法解决数据问题。采用ANSYS Workbench软件进行仿真模拟，不但可以得出抽象模型中相应的未知参数，还可对系统的运动微分方程进行求解，从而得到相应的固有频率，同时通过软件仿真分析还可得到与实际工况类似的工况条件。在实体建模的过程中，可采用两种方法：第一种方法可直接用 ANSYS Workbench 有限元软件自带的建模功能，对两个啮合的涡旋盘进行建模；第二种方法是通过其他三维建模软件对系统进行建模，之后导入到ANSYS Workbench中进行分析。两种建模方法各有利弊，如采用第一种建模方法，所得到的模型不需要经过转化，模型的所有信息会被准确地保留下来，所以对模型的分析更为准确，同时第一种方法更有利于模型的修正和参数化设计。众所周知,ANSYS Workbench软件侧重于对模型进行有限元分析，而对参数曲线的三维实体进行建模并不擅长，所以对于涡旋齿涡旋型线为渐开线的涡旋盘，在 ANSYS Workbench中不易建模，而在SolidWorks中建模却容易实现。故本文的三维建模采用第二种方法，即先使用SolidWorks 软件分别建立动涡旋盘和静涡旋盘的三维实体模型，然后在SolidWorks中对二者进行虚拟装配，最后将装配好的三维模型导入到 ANSYS Workbench 中进行有限元分析，以此来发挥各个软件的长处。

现以某型渐开线涡旋压缩机涡旋盘图纸为依据进行建模工作。建立的三维实体模型如图2所示。其中，动、静涡旋盘的端板厚度均为10mm，端板半径均为55mm。在建立三维实体模型的过程中，略去了润滑槽等非关键结构。在进行虚拟装配时的相关参数应按照表1中各公式经计算后得到的数据进行选取。

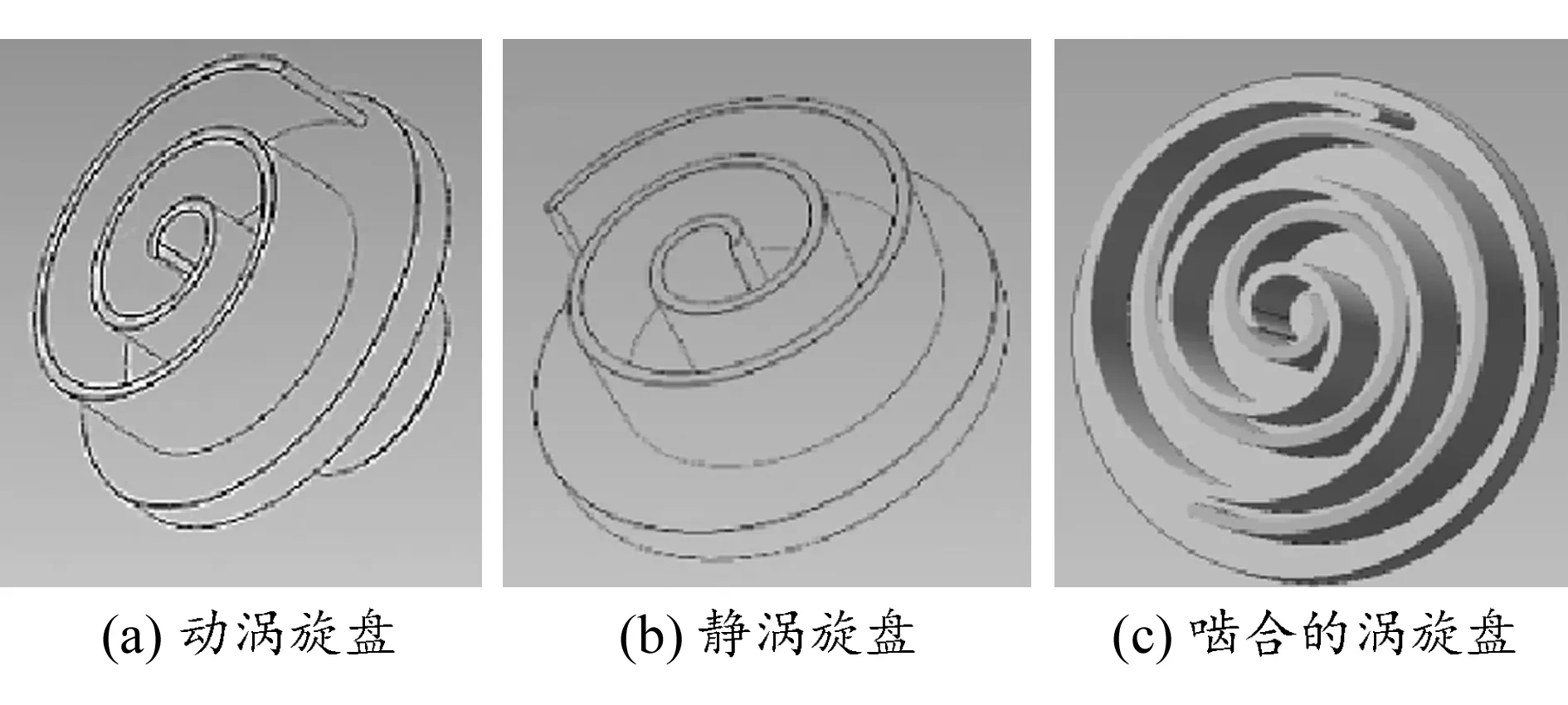
图2 动、静涡旋盘实体模型

项目计算公式参数取值基圆半径a/mm3渐开线节距P/mmP=2πa18.84渐开线发生角α/rad0.5涡旋体壁厚t/mmt=2aα3涡旋体高度h/mm27.5基圆中心距r/mmr=P/2-t6.42

进行虚拟装配后啮合的动、静涡旋盘系统实体模型如图2(c)所示，为看清啮合结构，已将静涡旋盘的端板剖去。

2 模态分析

对系统进行模态分析的目的在于得出该系统的自然频率，在进行涡旋盘系统设计时应避免外部振源的振动频率与该系统的自然频率相接近，以免发生共振导致系统工作不正常甚至破坏涡旋压缩机。对于振动系统来说，其振动微分方程为[5]：

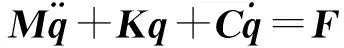
(2)

(K-ω2M)φ=0

(3)

式(3)是关于模态向量φ的n元线性齐次方程组，易知φ=0是方程的一个解，但它对工程来说没有意义，因为它表示各节点均没有发生振动。因此应该研究其非零解，式(3)有非零解必须满足其特征行列式为零这一条件，即：

Δ(ω2)=K-ω2M=0

(4)

通过式(4)求得的ω即为系统的自然频率，将ω代入式(3)就可求得系统的模态向量。模态分析是对系统振动进行分析的基础，如果不能得到系统的固有频率，那么在后续分析有外激振力作用下的系统受迫振动，即研究式(2)的解也就无从谈起。

2.1 涡旋盘的材料及网格划分

分析过程分为两组，即采用不同的材料进行对比分析。第一组材料是一种镁合金，第二组材料是一种灰口铸铁。两组材料在软件计算时所需要的物理量——弹性模量、泊松比及密度见表2。

表2 计算所需的物理量

网格划分采用自由网格划分方法，尺寸默认为 4.7mm，单元数为38 752，节点数为69 272，划分后的实体如图3所示。

图3 划分网格后的装配体

2.2 约束条件的设定

约束条件的设定对于在软件ANSYS Workbench中求解模型的振动问题起着非常重要的作用[8]。约束条件的本质是相应常微分方程的边界条件，相同的常微分方程在施加不同的边界条件后，得到的结果也往往不同。在实际的工况条件下，考虑到静涡旋盘与机架相连接，在轴向可有一定的弹性变形，因此没有设置静涡旋盘的约束条件为固定。而对于动涡旋盘来说，其右端与曲轴相连接，但曲轴不在本文研究的范围内，所以应对动涡旋盘的曲轴孔施加相应的约束。施加的边界条件如下：动涡旋盘曲轴孔固定，动涡旋盘绕x,y,z轴转动自由度均为零。静涡旋盘与动涡旋盘设置接触为bonded。静涡旋盘绕x,y,z轴转动自由度均为零。

2.3 分析结果

由于系统在各阶模态频率下都可能发生共振，将模态分析扩展到6阶。把所建立好的模型导入ANSYS Workbench中，对模型进行网格划分，之后添加相应的约束条件。运用软件ANSYS Workbench15.0分析的结果如图4、图5及表3、表4所示。

图5 灰口铸铁双涡旋盘啮合固有振型

Hz

表4 各阶模态最大位移 mm

3 结论

1)通过对由两种不同材料构成的涡旋盘的模态分析可知，两种材料的涡旋盘在低模态下的振动频率均相差不大，容易发生共振现象，在涡旋压缩机的设计阶段，应考虑优化涡旋压缩机的结构，并使得驱动电机的旋转频率及开关频率避开压缩机的固有频率，以避免在实际工作中，涡旋压缩机发生共振现象。

2)由于灰口铸铁材料的弹性模量比较大，所以在各阶模态振动下，由灰口铸铁制作的涡旋盘的最大位移均小于由镁合金材料制作的涡旋盘。

3)用镁合金材料制作的涡旋盘相比于用灰口铸铁制作的涡旋盘，其固有频率更高，在低模态下更不容易发生共振。同时用镁合金制作的涡旋盘更轻，更易加工成不同型线的涡旋盘，有助于实现压缩机的轻量化设计。

参考文献：

[1] 彭斌,朱兵国. 涡旋型线对涡旋压缩机性能的影响[J].流体机械,2016,44(6):17-23.

[2] 李超,谢文君,赵嫚.多场耦合作用下动涡旋盘的变形和应力研究[J].流体机械,2013,41(8):16-20.

[3] 赵嫚,李超,俞树荣,等.涡旋压缩机驱动轴承的力学特性研究[J].振动、测试与诊断,2013,33(1):18-20.

[4] 刘昌领,罗晓兰.基于 ANASYS的六缸压缩机连杆模态分析及谐响应分析[J].机械设计与制造,2013(3):26-29.

[5] 李超,张官正,刘兴旺,等.涡旋压缩机径向迷宫密封迷宫槽的优化研究[J].流体机械,2014,42(11):8-12.

[6] 汤俊雄,惠虎,王辰.沿海一高耸塔器顺风向风振响应研究[J].压力容器,2015,32(6):13-18.

[7] 来敏华.前汽封汽流窝动间歇性振动分析和对策[J].化工设备与管道,2015,52(4):63-65.

[8] 肖根福,刘国平,王俊亭,等.动网格在涡旋压缩机三维流场数值模拟中的应用[J].流体机械,2014,42(1):15-29.