多目标U型拆卸线平衡问题的Pareto蚁群遗传算法
2018-06-01张则强汪开普朱立夏程文明
张则强, 汪开普, 朱立夏, 程文明
(西南交通大学机械工程学院, 四川 成都 610031)
随着我国经济的高速增长,产品更新换代的步伐加快,产生了大量废旧机电产品,废旧机电产品的回收再利用是生态文明建设的重要组成部分.绿色发展已经成为国家战略,国务院印发的《中国制造2025》[1]中明确提出,要“发展循环经济,提高资源回收利用效率,构建绿色制造体系”.拆卸是实现资源回收再利用的关键一环,也是绿色制造系统的重要组成部分,通过拆卸可实现贵重材料和有价值零部件的回收,是构筑产品生命周期完整性与封闭性的必要环节.拆卸线是废旧机电产品规模化拆卸生产的最佳方式之一,具有规范性好、效率高等优点.然而在实际生产过程中,拆卸生产线上各工作站间普遍存在着作业不平衡等现象,对拆卸企业生产效率的提升产生了较大影响,由此产生了拆卸线平衡问题(disassembly line balancing problem, DLBP)[2],并引起了国内外学者的高度关注[3-16].
GUNGOR等[2]对多目标拆卸线平衡问题进行了全面描述,进而分析了影响拆卸线生产率的各种因素.传统的启发式算法[2-3]、数学规划法[4]在求解拆卸线平衡问题时能够得到精确解,但只适用于小规模问题.拆卸线平衡问题是NP (non-deterministic polynomial)完全问题[5],当拆卸任务规模增大到一定程度时,在有效时间内很难求得最优解.亚启发式算法[5-15]在求解不同规模任务的多目标拆卸线平衡问题时表现出良好的求解性能,能够得到较优解.文献[5-15]在描述拆卸线平衡问题时考虑了多个优化目标,但在处理多目标问题时却将其转化为为单目标问题,一次只能求得一个解,所得平衡方案无法均衡存在冲突关系的各目标.文献[16]应用Pareto蚁群算法在求解多目标拆卸线平衡问题上做了很好的研究工作,得到多个Pareto最优解,所得方案兼顾了各目标间的均衡性,但其求解性能还有进一步提升的空间.
文献[2-16]中拆卸线布局形式均为直线型,U型布局相较于直线型布局具有占地面积小、柔性高、生产效率高等优点,有助于生产线效率的进一步提高[17-18],基于此,U型布局在拆卸线中也得到了应用[19-20].但现有的文献多是对直线型拆卸线平衡问题展开研究,甚少有对U型拆卸线平衡问题(U-shaped disassembly line balancing problem, UDLBP)进行探讨.国外文献中,仅文献[19]采用协同蚁群算法求解随机混流U型拆卸线平衡问题,以最小化工作站空闲时间和停工概率为优化目标,采用单目标求解思想处理该问题,无法实现各目标间的均衡.国内方面,只有文献[20]应用人工蜂群算法按目标分级方式处理多目标U型拆卸线平衡问题,依然是将多目标问题转化为单目标问题进行求解.针对现有文献对多目标U型拆卸线平衡问题研究的不足,有必要对该问题展开研究.
蚁群算法和遗传算法在求解NP问题时具有良好的求解性能[5-7,21],将两种算法融合用于求解复杂离散问题,能够实现优势互补.文献[22]采用混合蚁群遗传算法求解复杂装配线平衡和调度问题,结果表明混合算法相对于单一算法求解质量显著提高.查阅相关文献,尚未有学者采用混合蚁群遗传算法求解U型拆卸线平衡问题.
鉴于现有文献对拆卸线平衡问题研究的不足,本文结合Pareto解集思想[23]以及蚁群算法和遗传算法求解NP问题的优势,提出一种求解U型拆卸线平衡问题的多目标Pareto蚁群遗传算法(ant colony and genetic algorithm, ACGA),改进算法的蚁群操作和遗传操作.通过对比测试与实例应用,验证了所提算法的求解性能.
1 多目标U型拆卸线平衡问题
1.1 U型拆卸线描述
传统的拆卸线一般采用直线型,待拆卸产品在直线排列的传动设备上传递,工人在传动设备的一侧进行拆卸作业,直至所需拆卸的作业任务完成为止,在传动设备的另一端输出废料,如图1所示,图中Ti(i=1,2,…,4)为工作站作业时间.直线型拆卸线具有布局简单,容易实现拆卸作业任务的自动化、规模化等优点.

图1 直线型拆卸线示意Fig.1 Schematic diagram of linear disassembly line
U型拆卸线是将拆卸传动装置沿逆时针方向按U型布置,工人可以在传动设备两侧作业.在同一个工作站内,工人可对无紧前任务或无紧后任务的零部件进行拆卸.相对于传统直线型拆卸线,U型拆卸线布局更加合理,可减少工人的行走距离,提高工作效率;待拆卸产品入口和废料出口在同一侧,可降低物流成本;同时,合理的任务分配能有效减少工作站数量.
现以含10个拆卸任务的某机械部件的拆卸线为例,对比U型拆卸线和直线型拆卸线的性能.图1中,箭头连接的任务间存在优先关系,各零部件的拆卸时间分别为2、4、3、5、6、2、4、4、3、3,设定生产节拍TC=12.由图1可知,直线型拆卸线中拆卸方案为:{1,2,3}→{4,5}→{6,7,8}→{9,10},一共开启4个工作站;每个工作站的作业时间分别为T1=9,T2=11,T3=10,T4=6,各工作站间作业时间非常不均衡.
将直线型拆卸线改为U型拆卸线,如图2所示,平衡方案为:{1,-10,-9,2}→{3,-8,4}→{5,6,-7},方案中负号表示拆卸位置位于U型拆卸线出口一侧,一共开启3个工作站,且每个工作站的作业时间都达到设定的生产节拍,各工作站间达到了完全均衡.通过上述对比可知,U型拆卸线布局较直线型拆卸线布局更具优势.

图2 U型拆卸线示意Fig.2 Schematic diagram of U-shaped disassembly line
1.2 数学模型
针对U型拆卸线平衡问题的特点,考虑了以下几种情况:为减少拆卸设施成本,应尽量减少开启工作站数目;为提高作业效率和公平性,应最大限度满足各个工作站间的均衡性;最大限度降低拆卸作业成本,以便实现经济效益最大化;同时应该避免拆卸方向频繁改变,尽量减少非作业时间.建立多目标U型拆卸线平衡问题模型[5,16]为
minf1=M;
(1)
(2)
(3)
(4)
(5)

(6)
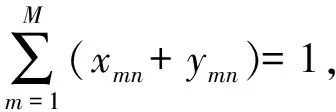
(7)
∀sij=1,
(8)
式中:M为工作站数;m为工作站编号;N为拆卸任务数;tn为第n个拆卸任务的作业时间;xmn为0-1分配变量,若第n个任务被分配到第m个工作站的入口侧,则xmn=1,否则xmn=0;ymn为0-1分配变量,若第n个任务被分配到第m个工作站的出口侧,则ymn=1,否则ymn=0;Un为第n个拆卸任务的单位时间拆卸成本;rn为序列中第n个拆卸任务的拆卸方向;Rn为拆卸序列中方向改变次数,若前后两任务的拆卸方向不同(rn≠rn-1),则Rn=1,否则Rn=0;i,j为拆卸序列中任务的编号;sij为任务i,j间优先关系值,若拆卸任务i是拆卸任务j的紧前任务,则sij=1,否则sij=0,构造任务间优先关系矩阵S,有S=[sij]N×N.
式(1)~(4)为U型拆卸线平衡问题的目标函数,分别表示最小化开启工作站数、平衡工作站的空闲时间、最小化拆卸成本、最小化拆卸方向改变次数,其中工作站的单位时间拆卸成本定义为该工作站内拆卸任务的最大单位时间拆卸成本,需要指出的是U型拆卸线中拆卸任务方向的改变不同于直线型拆卸线中工人进行作业任务的方向改变,而是生产线上拆卸任务方向的改变.
式(5)~(8)为U型拆卸线平衡问题的约束条件,式(5)表示拆卸生产线所开启的工作站数不少于理论工作站数,且每个工作站均在生产作业,所开启的工作站不应超过拆卸任务数;式(6)表示分配到每个工作站的作业任务时间上限为生产节拍;式(7)表示拆卸线为完全拆卸,所有零部件都必须进行拆卸作业,且每一项任务只能在一个工作站中完成;式(8)表示拆卸任务的进行须符合任务间的几何约束,即满足拆卸任务间的拆卸优先关系.
2 Pareto蚁群遗传算法
混合蚁群遗传算法很好的结合了蚁群算法和遗传算法的优点,具有更强的搜索能力[22],本文针对多目标U型拆卸线平衡问题的特点,结合Pareto解集思想,改进蚁群算法的初始可行解,构造遗传操作,提出Pareto蚁群遗传算法.
2.1 可行解的构造
在拆卸线平衡问题中,随机生成的序列不一定满足任务优先关系,故首先需要构造可行解.
用蚁群算法构造拆卸线平衡问题的可行解可视为蚂蚁在信息素浓度的指引下寻找下一个拆卸任务,蚂蚁经过的路径组成问题的拆卸序列,随着信息素的更新实现路径的寻优.
蚁群算法中启发式因子代表着选择下一个拆卸任务的期望程度.结合拆卸线平衡问题的特征,以最长拆卸作业时间、最小拆卸成本差距为启发式规则,构建任务l的启发式函数为
(9)
式中:Aj为当前位置j(j≥2)的候选任务集;l∈Aj;s∈Aj;k为位置j的前一项位置(即j-1)处所对应的任务.
为使蚂蚁以最大概率收敛到全局最优解,综合考虑多种规则,构造混合搜索机制[21],被分配到特定序列位置j的任务i为
(10)
式中:r为(0,1)间的随机数;r1、r2为定义的参数;τie为任务i到后续任务e的信息素;Aj为当前分配序列位置j的候选任务集;α为信息素权值;β为启发式信息权值.
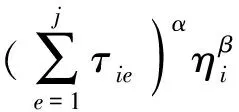
为保证可行解满足拆卸线实际生产情况,每一项任务的选择都要考虑拆卸优先关系约束.同时需判断每一项任务在U型拆卸线两侧中的位置:无紧前约束的任务位于U型入口侧,符号为“+”;无紧后约束的任务位于U型出口侧,符号为“-”;若拆卸任务既无紧前约束,也无紧后约束,则符号与前一个任务相同.
构造可行解的具体步骤如下:
(1) 从矩阵Y中按式(10)挑选任务i作为位置j处的任务,要求所选任务无紧前约束或无紧后约束,在矩阵中表现为行列全为零,并判断拆卸任务的符号;存在多个可选任务时,从可选任务集中随机挑选;
(2) 将与任务i有优先关系的约束从Y中删除:∀k∈{1,2,…,N},令yik=0,yki=0;
(3) 寻找下一位置处的任务,令j=j+1;
(4) 重复上述3步骤,完成所有任务分配.
2.2 Pareto解集的更新
在含D个目标的多目标问题中,给定两个可行拆卸序列X1、X2,若X1、X2满足
fd(X1)≤fd(X2), ∀d∈{1,2,…,D},
(11)
fd(X1) (12) 则称X1Pareto支配X2,记为X1X2. 若可行解X*满足:∃X使得XX*,则称X*为Pareto最优解或非劣解.所有X*的集合PS={X*|∃XX*}构成Pareto最优解集,对应目标函数值称为Pareto最优前沿. 根据可行解之间的支配关系,保留支配解于外部档案中,剔除非支配解,完成外部档案的更新. 采用非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)拥挤距离机制[23]评价外部档案中的非劣解,定义边界个体的拥挤距离L1=Lk=∞,拥挤距离表达式为 (13) 式中:g=2,…,k-1,k为非劣解的个数;fd,max、fd,min分别为第d个目标函数值的最大值和最小值. 蚂蚁在行走过后的路径上留下信息素,随着时间的推移,信息素会不断更新.局部信息素的更新使得蚂蚁能够摆脱已选任务的影响,跳出局部最优,增强探索未选任务的能力.蚂蚁将任务i分配到位置j,该路径上局部信息素更新方式为 τij=(1-ρ1)τij+ρ1τ0, (14) (15) 式中:ρ1为局部信息素挥发因子,0<ρ1<1;τ0为初始信息素. 在算法迭代过程中,只有全局最优的蚂蚁才允许释放信息素,所对应的拆卸方案路线上的信息素会增加,即非劣解所对应的拆卸方案存在信息素的增加,其他方案路线上不会有信息素增加.全局信息素增加方式为 τij=(1-ρ2)τij+ρ2Δτij, (16) (17) 式中:ρ2为全局信息素挥发因子,0<ρ2<1;q为调整参数. 在多目标拆卸线平衡问题中,无法直接通过某个目标值评价适应度的大小,而是根据可行解之间的支配关系评价个体的优劣,蚁群算法外部档案中非劣解均为可选的优质个体,随机挑选蚁群算法外部档案中两个非劣解作为下一步操作的个体. 在拆卸线平衡问题中,受任务间优先关系的约束,传统方法中随机交叉方式将产生大量不可行解,会降低算法效率.本文采用双点映射交叉的方式,具体操作过程如图3所示. 图3 交叉操作示意Fig.3 Schematic diagram of crossover operation 在父代Xcurrent 1、Xcurrent 2中随机选取两点作为交叉点,保持Xcurrent 1中交叉点1之前的序列{6,3,7}和交叉点2之后的序列{2,4,9}不变,两交叉点之间的序列{8,5,1}在Xcurrent 2中顺序为{1,5,8},组成子代Xnew 1={6,3,7,1,5,8,2,4,9},因{1,5,8}在Xcurrent 2中满足优先关系,则生成的子代必然满足优先关系.同理可以得到子代Xnew 2.因U型拆卸线中当前拆卸任务可从无紧后任务中选择,导致交叉后的任务可能在其紧后任务之前,不满足拆卸优先关系,需要重新选择交叉点. 同交叉操作类似,受任务间优先关系约束,变异操作中随机交换两点将产生大量不可行解.本文采用如图4所示的单点变异操作.在父代Xcurrent中随机选取一点作为变异点4,受优先关系约束,需要找到任务4的紧前任务和紧后任务,而任务4可以变换的位置在最近的紧前任务8和最近的紧后任务2之间,即任务1、5之前或是任务9、6之后,随机选择一点进行插入,如选择任务9之后,则子代Xnew={3,8,1,5,9,4,6,2,7}.在挑选变异位置时,若没有可选的插入位置,则需重新选择变异点. 图4 变异操作示意Fig.4 Schematic diagram of mutation operation 在上述定义的基础上,求解多目标U型拆卸线平衡问题的Pareto蚁群遗传算法具体实现步骤如下: 步骤1算法参数设定:种群规模Nant,最大迭代次数T,外部档案规模N0,信息素权值α,启发式信息权值β,参数r1、r2,局部信息素挥发因子ρ1,全局信息素挥发因子ρ2,调整参数q,交叉概率Pc,变异概率Pm,生产节拍TC; 步骤2开始循环计数,令t=1;初始化蚁群,建立Pareto解集,令外部档案Q=∅; 步骤3根据2.1节内容生成可行拆卸序列,按式(14)更新局部信息素; 步骤4计算目标函数值,筛选种群非劣解,更新外部档案Q; 步骤5执行选择、交叉、变异等遗传操作; 步骤6对遗传操作后的个体筛选种群非劣解,更新外部档案Q; 步骤7按式(16)更新全局信息素; 步骤8计算Q中非劣解个数NQ:若NQ>N0,按式(13)评价非劣解,选取N0个Lg较大的非劣解置于Q中,进入下一步;否则,直接进入下一步; 步骤9若t 步骤10算法终止,得到最优拆卸方案. 所设计的Pareto蚁群遗传算法部分参数设置如下:α=1.5,β=1.5,r1=0.6,r2=0.9,ρ1=0.4,ρ2=0.3,q=10,Pc=0.9,Pm=0.1.其它参数需根据实例具体情况而设定.选用MATLAB 7.11进行测试验证. 以文献[16]中算例为研究对象,验证所提算法在的求解性能.该算例相关数据见文献[16].该文献的优化目标为最小化平均闲置率Fidle、最大化负荷均衡指标Fsmooth、最小化拆卸成本Fcost.目标函数Fcost与本文目标函数f3相同,引入该文献的前两个目标函数,如下式(18)、(19)所示,将多目标函数转化为式(20). (18) (19) minF=min(Fidle,1-Fsmooth,Fcost). (20) 现将文献[16]利用多目标Pareto蚁群算法(ant colony optimization, ACO)求得的6种平衡方案结果列于表1中.采用本文所提多目标Pareto蚁群遗传算法对该算例进行求解,算法需设定的参数有:Nant=50,T=200,N0=8,TC=600.共求得8个非劣解的Pareto解集,将非劣解的平衡方案列于表2中. 表1 文献[16]Pareto ACO求解结果Tab.1 Solution results of Pareto ACO in literature [16] 将表2中Pareto ACGA结果与表1中Pareto ACO结果进行比较.在Fidle指标上,ACGA的8个非劣解均求得最优解0.057 9,平均值为0.057 9,ACO只有3个非劣解求得最优解0.057 9,其他3个解为0.175 7,平均值为0.116 8,ACGA在Fidle上较ACO提高了50.43%;在Fsmooth指标上,ACGA结果范围为91.5%~99.0%,平均值为95.31%,ACO结果范围为85.9%~97.5%,平均值为92.31%,ACGA在Fsmooth上较ACO方案提高了3.25%,ACGA平衡率更高;在Fcost指标上,ACGA结果在130.332~146.994之间,平均值为139.430,ACO结果在150.546~173.388之间,平均值为162.310,ACGA在Fcost上较ACO提高了14.10%,ACGA成本更低.综上单目标对比可知ACGA结果明显优于ACO. 综合3个目标比较:按Pareto支配关系的定义,ACGA的非劣解1、7、8支配ACO的所有非劣解;ACGA的非劣解2、3支配ACO的非劣解1、3,与ACO的其他4个非劣解互不占优;ACGA的非劣解4、6支配ACO的非劣解1、2、3,与ACO另3个非劣解互不占优;ACGA的非劣解5支配ACO的非劣解1、2、3、6,与ACO的另两个非劣解4、5互不占优.通过对比可知,所提多目标Pareto ACGA能有效求解U型拆卸线平衡问题,且求解性能较多目标Pareto ACO更具优势. 表2 所提Pareto ACGA求解平衡方案Tab.2 Balance schemes of proposed Pareto ACGA 现以某型号打印机拆卸线为研究对象,分析所提多目标Pareto ACGA在U型拆卸线实例中的应用情况.该拆卸线所涉及到的零件的拆卸时间t(s)、单位时间拆卸成本U(元/s)、拆卸方向r及其紧前任务P等拆卸信息如表3所示.表3中拆卸时间是经多次拆卸计时取平均值测定. 表3 拆卸任务相关信息表Tab.3 Related data information of printer disassembly tasks 综合实际拆卸生产情况,设定生产节拍TC=145,算法其他参数设置为:Nant=50,T=100,N0=8.经20次运行,计算平均运行时间为54.36 s,每次运行均能求得8个非劣解,表明所提算法求解结果具有多样性.取其中一次结果的非劣解任务分配方案列于表4中. 由表4可知,8种平衡方案均求得5个最优工作站,故在方案选择上只需考虑工作站空闲指标、拆卸成本以及拆卸方向改变次数.非劣解在3个目标f2、f3、f4的空间分布如图5所示. 由表4的求解结果对比分析可知:8个方案的空闲指标范围在506~718之间,若要求空闲指数最小,可以考虑方案8;拆卸成本范围为6.192~6.917,若要求成本最小,可以选择方案7;拆卸方向改变次数范围为26~39,若要求拆卸方向改变次数最少,可以选择方案4. 结合表4求解结果与图5方案结果空间分布对比分析,综合考虑某两个指标进行方案选择:若优先考虑空闲指标和拆卸成本,可以选择方案1或方案6;若要求空闲指数小和拆卸方向改变次数少,可以选择方案2或方案8;若要求拆卸成本低、拆卸方向改变次数少,可以选择方案3、方案5或方案7.所提算法求得的8种平衡方案可以为决策者提供多种选择,避免方案选择上的盲目性. 表4 Pareto ACGA非劣解的平衡方案Tab.4 Non-inferior solution balance schemes of Pareto ACGA 注:•表示方案图5 ACGA非劣解在f2、f3、f4上空间分布Fig.5 Non-inferior solutions spatial distribution of f2, f3, f4 (1) 针对传统直线型拆卸线的不足,构造了一种更符合实际生产情况的U型拆卸线模型,并设计了一种基于Pareto解集的多目标蚁群遗传算法,克服了传统方法求解多目标问题的缺陷,实现了求解结果的有效性与多样性. (2) 蚁群遗传算法将蚁群算法和遗传算法各自的优点相结合,能有效避免算法陷入局部最优.改进蚁群算法的启发式规则,使任务的分配更符合问题的实际生产情况.通过拥挤距离评价筛选机制,实现了精英保留.采用拥挤度更新蚂蚁的全局信息素,能够平衡各个目标对信息素浓度的影响.将非劣解作为遗传操作的个体,且遗传操作的结果正反馈于最优路径上的信息素浓度,丰富了蚂蚁的寻优路径,同时加快了算法的收敛速度. (3) 运用所提算法对52项拆卸任务的测试问题进行验算,并与多目标Pareto蚁群算法进行对比,所提算法求解方案优于Pareto蚁群算法的方案,验证了所提算法求解多目标U型拆卸线平衡问题的有效性.最后,将所提算法应用于具有55项拆卸任务的某打印机拆卸实例中,得到8种候选平衡方案,为决策者提供了广泛的决策空间. [1] 国务院. 国务院关于印发《中国制造2025》的通知[J]. 中华人民共和国国务院公报,2015(16): 10-26. [2] GUNGOR A, GUPTA S M. Disassembly line in product recovery[J]. International Journal of Production Research, 2002, 40(11): 2569-2589. [3] AVIKAL S, MISHRA P K, JAIN R. A Fuzzy AHP and PROMETHEE method-based heuristic for disassembly line balancing problems[J]. International Journal of Production Research, 2014, 52(5): 1306-1317. [4] BENTAHA M L, BATTAIA O, DOLGUI A. Lagrangian relaxation for stochastic disassembly line balancing problem[J]. Procedia CIRP, 2014(17): 56-60. [5] MCGOVERN S M, GUPTA S M. A balancing method and genetic algorithm for disassembly line balancing[J]. European Journal of Operational Research, 2007, 179(3): 692-708. [6] 朱兴涛,张则强,朱勋梦,等. 求解多目标拆卸线平衡问题的一种蚁群算法[J]. 中国机械工程,2014,25(8): 1075-1079. ZHU Xingtao, ZHANG Zeqaing, ZHU Xunmeng, et al. An ant colony optimization algorithm for multi-objective disassembly line balancing problem[J]. China Mechanical Engineering, 2014, 25(8): 1075-1079. [7] MCGOVERN S M, GUPTA S M. Ant colony optimization for disassembly sequencing with multiple objectives[J]. The International Journal of Advanced Manufacturing Technology, 2006, 30(5): 481-496. [8] KALAYCI C B, GUPTA S M. A particle swarm optimization algorithm for solving disassembly line balancing problem[C]∥Proceedings for the Northeast Region Decision Sciences Institute.[S.l.]: Newport, 2012: 347-357. [9] KALAYCI C B, GUPTA S M, NAKASHIMA K. Bees colony intelligence in solving disassembly line balancing problem[C]∥Proceedings of the 2011 Asian Conference of Management Science and Applications. Sanya: [s.n.], 2011: 34-41. [10] 张则强,胡扬,陈冲. 求解拆卸线平衡问题的改进人工蜂群算法[J]. 西南交通大学学报,2016,51(5): 910-917. ZHANG Zeqiang, HU Yang, CHEN Chong. An improved artificial bee colony algorithm for disassembly line balancing problem[J]. Journal of Southwest Jiaotong University, 2016, 51(5): 910-917. [11] KALAYCI C B, POLAT O, GUPTA S M. A variable neighbourhood search algorithm for disassembly lines[J]. Journal of Manufacturing Technology Management, 2015, 26(2): 182-194. [12] TUNCEL E, ZEID A, KAMARTHI S. Solving large scale disassembly line balancing problem with uncertainty using reinforcement learning[J]. Journal of Intelligent Manufacturing, 2014, 25(4): 647-659. [13] KALAYCI C B, GUPTA S M. Tabu search for disassembly line balancing with multiple objectives[C]∥Proceedings of the 41st International Conference on Computers & Industrial Engineering. Los Angeles: [s.n.], 2011: 477-482. [14] KALAYCI C B, GUPTA S M, NAKASHIMA K. A simulated annealing algorithm for balancing a disassembly line[C]∥Proceedings of the Seventh International Symposium on Environmentally Conscious Design and Inverse Manufacturing. Netherlands: [s.n.], 2011: 713-718. [15] METE S, CIL Z A, AGPAK K, et al. A solution approach based on beam search algorithm for disassembly line balancing problem[J]. Journal of Manufacturing Systems, 2016, 41: 188-200. [16] 丁力平,谭建荣,冯毅雄,等. 基于Pareto蚁群算法的拆卸线平衡多目标优化[J]. 计算机集成制造系统,2009,15(7): 1406-1413. DING Liping, TAN Jianrong, FENG Yixiong, et al. Multiobjective optimization for disassembly line balancing based on Pareto ant colony algorithm[J]. Computer Integrated Manufacturing Systems, 2009, 15(7): 1406-1413, 1429. [17] ALAVIDOOST M, BABAZADEH H, SAYYARI S. An interactive fuzzy programming approach for bi-objective straight and U-shaped assembly line balancing problem[J]. Applied Soft Computing, 2016, 40: 221-235. [18] ALAVIDOOST M H, ZARANDI M H, TARIMORADI M, et al. Modified genetic algorithm for simple straight and U-shaped assembly line balancing with fuzzy processing times[J]. Journal of Intelligent Manufacturing, 2017, 28(2): 313-336. [19] AGRAWAL S, TIWARI M K. A collaborative ant colony algorithm to stochastic mixed-model U-shaped disassembly line balancing and sequencing problem[J]. International Journal of Production Research, 2008, 46(6): 1405-1429. [20] 李明,张则强,胡扬. U型布局的拆卸线平衡问题及其求解算法研究[J]. 现代制造工程,2015(7): 7-12. LI Ming, ZHANG Zeqaing, HU Yang. Research on U-shaped disassembly line balancing problem and solving algorithm[J]. Modern Manufacturing Engineering, 2015(7): 7-12. [21] 张则强,胡俊逸,程文明. 第Ⅰ类双边装配线平衡问题的改进蚁群算法[J]. 西南交通大学学报,2013,48(4): 724-730. ZHANG Zeqiang, HU Junyi, CHENG Wenming. Improved ant colony algorithms for two-sided assembly line balancing problem of type Ⅰ[J]. Journal of Southwest Jiaotong University, 2013, 48(4): 724-730. [22] KUCUKKOC I, ZHANG D Z. Integrating ant colony and genetic algorithms in the balancing and scheduling of complex assembly lines[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(1/2/3/4): 265-285. [23] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.2.3 信息素的更新
2.4 选择操作
2.5 交叉操作
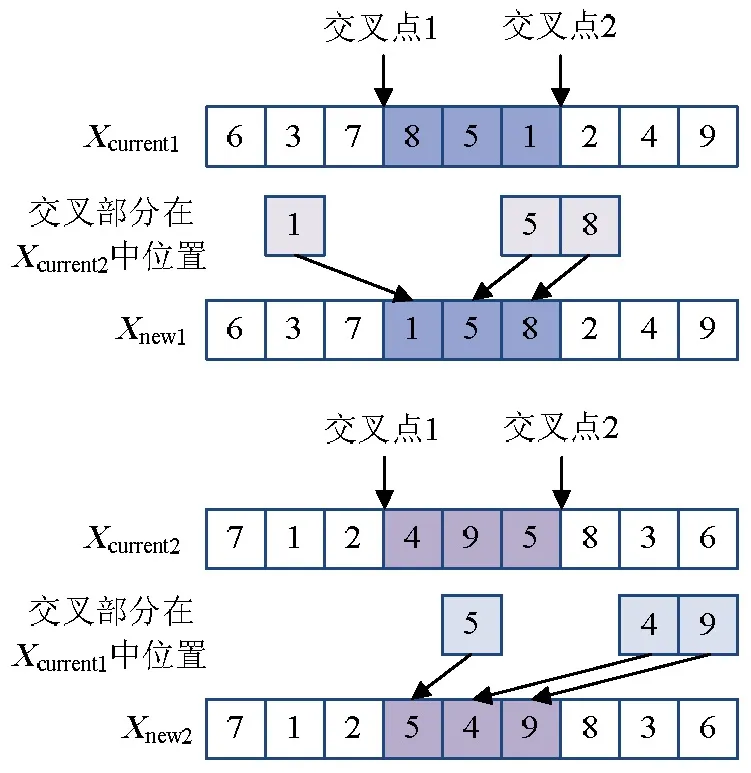
2.6 变异操作
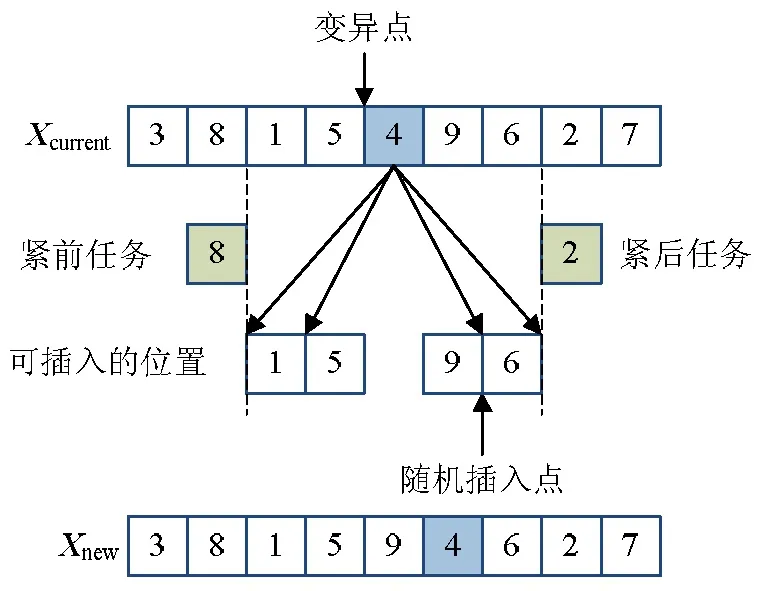
2.7 算法步骤
3 算法验证与实例应用
3.1 算法验证


3.2 实例应用
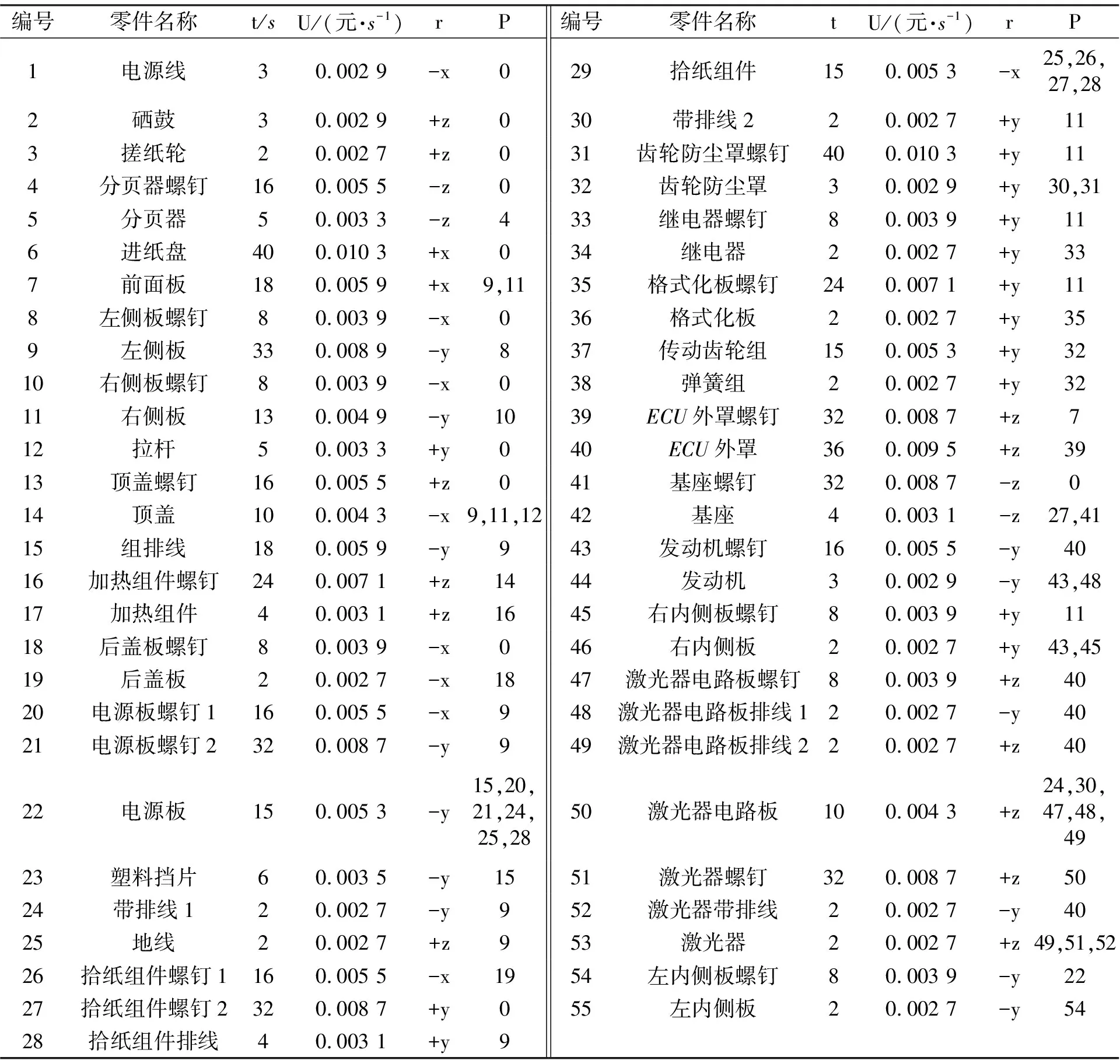

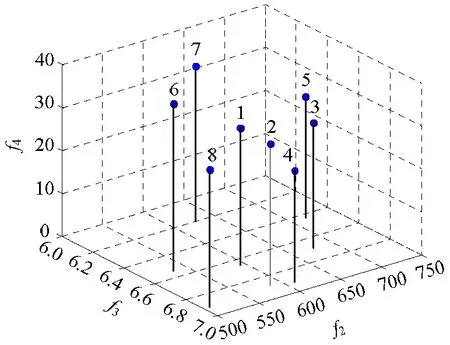
4 结 论
