带有UKBF的船舶动力定位预测控制器设计
2018-06-01苏义鑫张华军
苏义鑫, 赵 俊, 张华军
(武汉理工大学自动化学院, 湖北 武汉 430070)
随着人们对海洋资源开发的深入,船舶动力定位(dynamic positioning,DP)系统在深水定点作业中得到越来越广泛的应用.由于船舶自身的非线性特性和定位过程中受到海浪、海风等随机扰动的影响,研究人员在动力定位系统中应用了各种先进的滤波和控制技术以提高定位性能.针对船舶动力定位过程中的滤波问题,目前多利用扩展卡尔曼滤波算法[1]来解决.扩展卡尔曼滤波算法是采用高效率递归方式获得最小方差的最优估计算法[2],是进行状态估计与预测的有力工具,但扩展卡尔曼滤波算法需将非线性模型线性化,而线性化可能给估计带来误差,且计算较为复杂.文献[3]中采用粒子滤波算法估计船舶运动状态,无需线性化,但粒子滤波算法存在样本退化的问题.文献[4-5]中应用无迹卡尔曼滤波算法估计船舶状态,但需对系统模型进行离散化,可能会产生截断误差.文献[6]中提出了一种无迹卡尔曼布西滤波(unscented Kalman-Bucy filtering,UKBF)算法,该算法应用确定性采样策略逼近非线性分布,防止了样本退化;同时,该算法不需要对非线性模型进行线性化和离散化,防止了由二者带来的误差过大和难以计算的问题[7].
针对船舶动力定位非线性控制,文献[8-9]中分别给出了一种模糊动力定位控制器,这些控制器具有较强的鲁棒性,但针对不同船舶的模糊规则相差较大.文献[10]中提出了一种滑模动力定位控制器,该控制器具有物理实现简单和鲁棒性强的特点,但滑模控制器的抖振问题对推进器的磨损较大.文献[11]中应用非切换解析模型预测控制(non-switch analytic model predictive control, NSAMPC)方法设计动力定位控制器,取得了较好的控制效果.
本文将UKBF与NSAMPC相结合提出一种船舶动力定位控制器设计方法.根据船舶运动模型,利用UKBF方法估计船舶运动状态;结合相对阶概念应用NSAMPC方法设计船舶动力定位预测控制器,该方法不仅能够解决动力定位过程中的推力约束,而且还能够提高推进器输出的平滑度.
1 船舶运动数学模型
对于水面船舶的动力定位,只需考虑船舶在3个自由度上的运动,分别为纵荡、横荡和艏摇[11].船舶低速运动下3个自由度船舶运动模型[12-13]如式(1)所示
若令:
x=[xyψuvr]T;
u=[τXτYτN]T;
y=[y1y2y3]T=[xyψ]T.
将式(1)整理为规范形式,并考虑过程扰动和测量噪声对船舶运动的影响,则有式(2).
(1)
式中:x、y、ψ分别为船舶的纵坐标、横坐标和艏向角;u、v、r分别为船舶的纵荡速度、横荡速度和艏摇角速度;τX、τY、τN分别为纵向推力、横向推力和艏摇力矩;mi0j、di0j(1≤i0≤3,1≤j≤3)分别为惯性系数和阻尼系数;y1、y2、y3为系统输出.
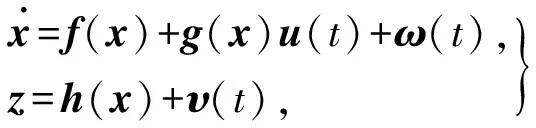
(2)
式中:z=[z1z2z3]T为测量输出;
ω(t)和υ(t)为零均值白噪声;
(3)
g(x)=[g1(x)g2(x)g3(x)]=
(4)
h(x)=[h1h2h3]T=[xyψ]T.
(5)
2 动力定位系统控制器设计
本文将连续非线性滤波方法UKBF与NSAMPC相结合,设计船舶DP非线性控制器,系统结构如图1所示.
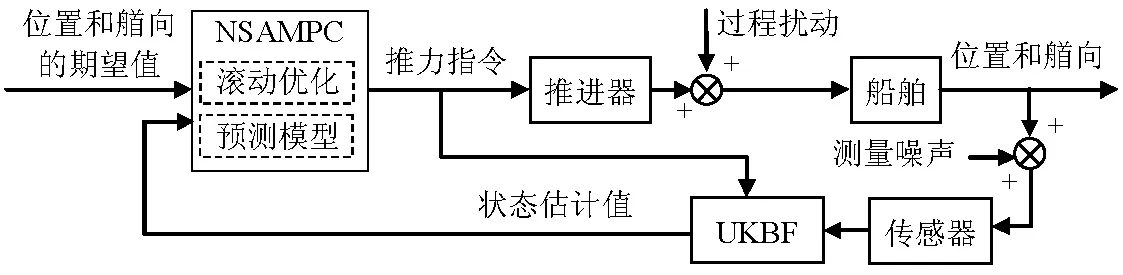
图1 船舶DP控制系统结构Fig.1 Structure of the proposed marine DP control system
2.1 UKBF算法
UKBF运用确定性采样方式逼近非线性分布,不需要对非线性模型进行线性化和离散化,防止了由二者带来的误差过大和难以计算的问题,且无需计算Jacobian和Hessian矩阵,能有效防止计算量过大或难以计算等问题.
给定连续非线性系统
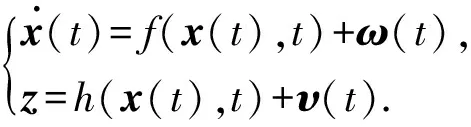
设:Q(t)为协方差矩阵(ω(t));Qc(t)为谱密度(ω(t));R(t)为协方差矩阵(υ(t));Rc(t)为谱密度(υ(t)).
首先选取Sigma点阵X(t),然后在系统状态和测量过程的有限连续时域内,应用无迹卡尔曼滤波的随机微分方程求解Sigma点的状态均值m(t),将其作为系统状态的估计值,即
K(t)(z(t)-h(x(t),t)ωm),
式中:K(t)为滤波器增益;ωm为权值矩阵.
2.2 UKBF滤波器设计
将式(2)转换成式(6).
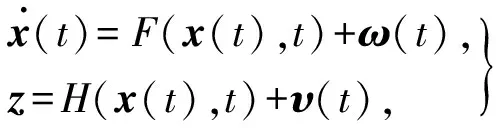
(6)
式中:x(t)∈Rn;
F(x(t),t)=f(x(t),t)+g(x(t),t)u(t);
H(x(t),t)=h(x(t)).
设:Δt为采样周期;Q(t)≈Qc(t)Δt;R(t)≈Rc(t)Δt.
选取近似采样点Sigma,Sigma点矩阵X(t)定义为
X(t)=[m(t) …m(t)]+
(7)

P(t)为Sigma点的状态协方差矩阵;
X(t)∈Rn×dS,为Sigma点的矩阵(dS为Sigma点个数,dS=2n+1).
连续UKBF递推过程的微分方程为
X(t)=X(t)WHT(X(t),t)×
[R(t)Rc(t)RT(t)]-1,
(8)
K(t)[z(t)-H(X(t),t)ωm],
(9)
FT(X(t),t)WXT(t)+Q(t)Qc(t)QT(t)-
K(t)R(t)Rc(t)RT(t)KT(t),
(10)
式中:
ωm=[Wm(0)…Wm(2n)]T,
W=(I-[ωm…ωm])×
diag(Wc(0),…,Wc(2n))×
(I-[ωm…ωm])T,
其中:Wm(0)=λ/(n+λ),
Wc(0)=λ/(m+λ)+(1-α2+β),α、β分别为设定参数,
Wm(i1)=1/2(n+λ),i1=1,…,2n,
Wc(i1)=1/2(n+λ),i1=1,…,2n.
采用连续表达式(8)~(10)计算得到的状态均值m(t),该值作为动力定位系统在t时刻的状态估计值.
2.3 非切换解析模型预测控制器设计
本文采用的滚动时域内的目标函数如式(11)所示.
(11)
式中:T为预测周期;
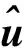
τ为滚动时域内的时间;
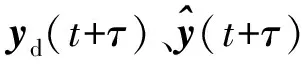
通常μ1、μ2为非负数,μ3为正数,依次为系统输出约束、控制输入、跟踪误差所占比重的反映,加有上标“^”的变量为预测变量.

(12)
其初始状态为系统的当前状态,即
(13)
根据式(12)、(13)可以预测[t,t+T]时间段内的系统输出.通过目标函数J的最小化,求取[t,t+T]时间段内的最优控制输入.
综上所述,非线性模型预测控制可以描述为
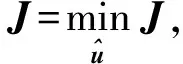
(14)
式(12)、(13)是式(14)的约束.

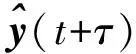
(15)
式中:

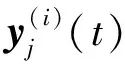
因此,式(11)所示的目标函数J的N阶泰勒级数展开可以近似为
(16)
式中:
M=μ1τ(τ)τT(τ)|τ=T+

式(14)等价于
(17)
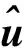
(18)
(19)
(20)
(21)
式中:
用ρi3j(1≤i3≤l, 1≤j≤m)表示控制输入ui3到系统输出yj的相对阶,相对阶的计算法方法可以参见文献[14].经计算可得,对所有状态满足Lg3Lfh3≠0,因此,ρ33可确定相对阶ρ11、ρ12、ρ13、ρ21、ρ22、ρ23、ρ31和ρ32.在某些状态下为0,则ρ11、ρ12、ρ13、ρ21、ρ22、ρ23、ρ31、ρ32是不确定相对阶.
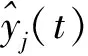
qi3(x)=[q1,i3(x)q2,i3(x)q3,i3(x)]T.
(22)

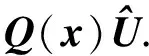
(23)

q1T(x)M(q0-yd)+
(24)
式中:
可由式(24),得到NSAMPC的解,取其初值,即为船舶动力定位的NSAMPC控制律,即
q1T(x)M(q0-yd).
(25)

3 仿 真
为了验证本文提出的船舶动力定位控制方法的有效性,分别对动力定位NSAMPC控制器,带有EKF的动力定位PID控制器和带有UKBF的动力定位NSAMPC控制器进行仿真.
主要参数:
船长76.2 m,船宽18.8 m,船舶净重4 200 t,主发动机功率3 533 kW,纵向推力(kN)[-1 000,1 000],横向推力(kN)[-300,300],艏摇力矩(kN·m)[-7 620,7 620].
m11=1.127 4,m22=1.890 2,m23=-0.074 4,m32=-0.074 4,m33=-0.127 8,d11=-0.035 8,d22=-0.118 3,d23=-0.012 4,d32=-0.004 1,d33=-0.030 8.
船舶的起始位置为(0 m,0 m,0°),定位位置为(0 m,50 m,0°),滤波采样间隔Δt=0.1 s,系统随机扰动的均值为0,协方差为diag(10-2,10-2,10-2,10-2,10-2,10-2),测量噪声的均值为0,协方差为diag(1,1,10-1).
设定参数:
κ=-2,α=0.5,β=2,T=1.4 s,仿真时长取500 s,μ1=1.0,μ2=0.05,μ3=0;PID控制器参数KPx=0.08,KIx=0.001,KDx=0.8,KPy=8,KIy=0.000 01,KDx=5,KPψ=10,KIψ=0.000 1,KDψ=6.
应用带有UKBF的动力定位NSAMPC控制器的船舶的位置和艏向的测量值和估计值,以及应用带有EKF的动力定位PID控制器的船舶位置和艏向的估计值如图2所示,图中:实线为应用带有UKBF的动力定位NSAMPC控制器的船舶位置和艏向的测量值;虚线为其估计值,点线为应用带有EKF的动力定位PID控制器的船舶位置和艏向的估计值.
从图2可以看出,系统的测量输出与滤波器输出相比,滤波器输出更加平滑.北向位置调节时间小于40 s,超调量不超过5%;东向位置调节时间小于60 s,超调量不超过5%;艏向角度的最大偏移量小于1.5°.系统的稳态输出的均值、方差分别为(49.99 m,50.01 m,-0.01°)和(0.012 8 m,0.024 5 m,0.000 4°),可见系统稳态输出的均值与设定值相差不大,方差很小.
从图2(a)、(b)可以看出,与应用带有EKF的动力定位PID控制器的船舶相比,应用带有UKBF的动力定位NSAMPC控制器的船舶的北向位置调节时间短、超调量小,船舶的东向位置调节时间短.应用带有UKBF的动力定位NSAMPC控制器,不带有UKBF的动力定位NSAMPC控制器和带有EKF的动力定位PID控制器的船舶的推力和力矩如图3所示,图中:实线为应用不带有UKBF的动力定位NSAMPC控制器的船舶推力和力矩;虚线为应用带有UKBF的动力定位NSAMPC控制器的船舶推力和力矩,点线为应用带有EKF的动力定位PID控制器的船舶推力和力矩.
从图3可以看出,应用带有UKBF的动力定位NSAMPC控制器的船舶推力和力矩是连续的,且推力和力矩波动更小.
从图3(a)可以看出,应用带有UKBF的动力定位NSAMPC控制器的船舶的纵向推力在稳态阶段波动较小;
从图3(b)可以看出,应用带有UKBF的动力定位NSAMPC控制器的船舶横向推力满偏次数较少,在稳态阶段波动较小;
从图3(c)可以看出,应用带有UKBF的动力定位NSAMPC控制器的船舶艏摇力矩满偏次数较少,在稳态阶段波动较小.
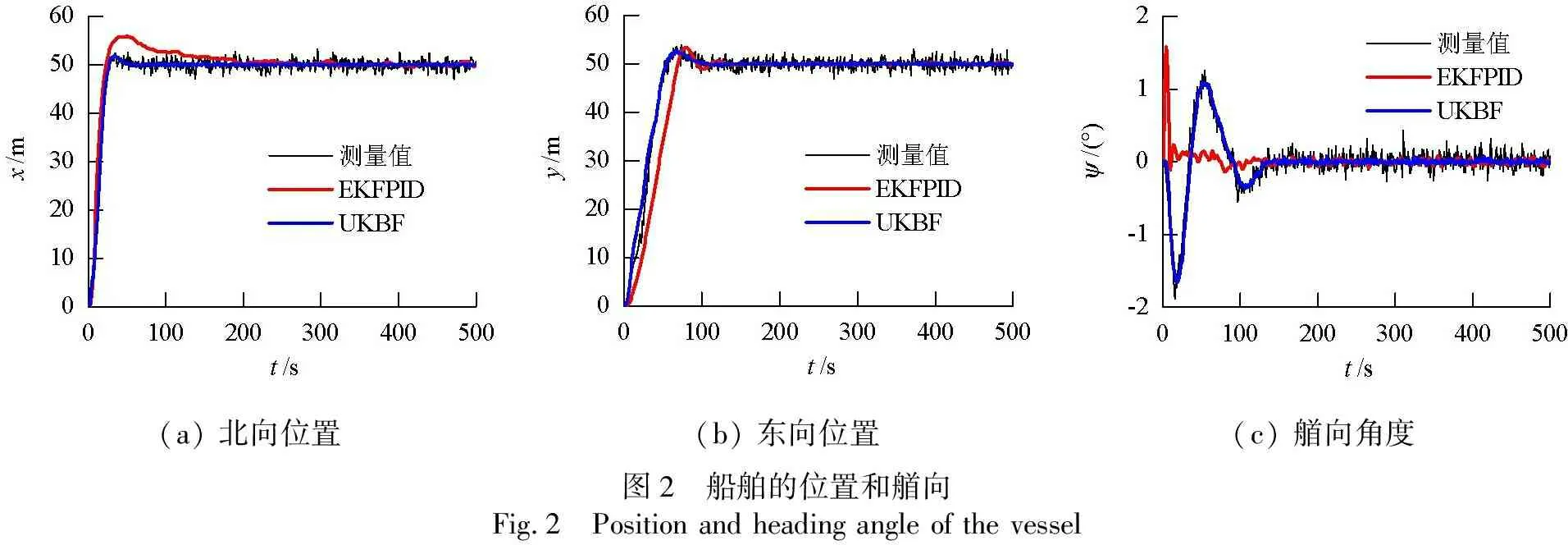
(a) 北向位置(b) 东向位置(c) 艏向角度图2 船舶的位置和艏向Fig.2 Position and heading angle of the vessel

(a) 纵向推力(b) 横向推力(c) 艏摇力矩图3 船舶纵向推力、横向推力和艏摇力矩Fig.3 Longitudinal thrust,lateral thrust and moment of the vessel
综合以上分析可得,采用本文所设计的控制器时,系统具有较强的抗随机扰动能力,能使船舶较快到达指定位置,并且控制力和力矩连续、在稳态阶段波动较小.
4 结 论
本文将UKBF与NSAMPC相结合,用于设计船舶动力定位非线性控制器,应用UKBF连续滤波方法设计了非线性系统的滤波器,产生船舶状态的估计值;应用NSAMPC方法对动力定位船舶进行控制.该控制器是非奇异的,较好地解决了相对阶不确定的系统控制问题,避免了由状态切换可能引起的系统振荡.仿真结果表明,本文设计的控制器能使船舶较快到达指定位置,并且控制力和力矩连续、在稳态阶段波动较小,有利于减少推进器的磨损.
[1] GRIMBLE M J, PATTON R J, WISE D A. The design of dynamic ship positioning control systems using extended Kalman filtering techniques[C]∥OCEANS’79. [S. l.]:IEEE, 1979: 488-497.
[2] 蒋伊琳,张芳园. 基于自然选择粒子群的时钟同步算法[J]. 西南交通大学学报,2017,52(3): 593-599.
JIANG Yilin, ZHANG Fangyuan. Clock synchroniza-tion algorithm based on particle swarm optimization with natural selection[J]. Journal of Southwest Jiaotong University, 2017, 52(3): 593-599.
[3] GGERSIMO G R. Sensor fusion-based dynamic positioning of ships using extended Kalman and particle filtering[J]. Robotica, 2013, 31(3): 389-403.
[4] WANG Xiaofei, ZOU Zaojian, WANG Yang, et al. Path following control of underactuated ships based on unscented Kalman filter[J]. Journal of Shanghai Jiaotong University, 2010, 15(1): 108-113.
[5] JAYASIRI A, NANDAN A, IMTIAZ S, et al. Dynamic positioning of vessels using a UKF-based observer and an NMPC-based controller[J]. IEEE Transactions on Automation Science & Engineering, 2017, 14(4): 1778-1785.
[7] 苏义鑫,赵俊. 带有UKF滚动时域估计的船舶动力定位控制器设计[J]. 哈尔滨工程大学学报,2016,37(10): 1381-1386,1393.
SU Yixin, ZHAO Jun. Dynamic positioning controller with UKF moving horizon estimation[J]. Journal of Harbin Engineering University, 2016, 37(10): 1381-1386,1393.
[8] HU X, DU J, SHI J. Adaptive fuzzy controller design for dynamic positioning system of vessels[J]. Applied Ocean Research, 2015, 53: 46-53.
[9] NGONGI W E, DU J, WANG R. Robust fuzzy controller design for dynamic positioning system of ships[J]. International Journal of Control, Automation and Systems, 2015, 13(5): 1294-1305.
[10] PATHE D T M, LI H, BIAN G. Switching surface design for nonlinear systems: the ship dynamic positioning[J]. Telkomnika Indonesian Journal of Electrical Engineering, 2014, 12(4): 2439-2447.
[11] 王元慧,隋玉峰,吴静. 基于非线性模型预测的船舶动力定位控制器设计[J]. 哈尔滨工程大学学报,2013,34(1): 110-115.
WANG Yuanhui, SUI Yufeng, WU Jing. Marine dynamic position system based on nonlinear model predictive control[J]. Journal of Harbin Engineering University, 2013, 34(1): 110-115.
[12] 张金龙,徐慧,刘京南,等. 基于模糊神经网络的精密角度定位PID控制[J]. 仪器仪表学报,2012,33(3): 549-554.
ZHANG Jinlong, XU Hui, LIU Jingnan, et a1. PID control based on fuzzy neural network for precision angular alignment[J]. Chinese Journal of Scientific Instrument, 2012, 33(3): 549-554.
[13] KHAC D D. Global robust and adaptive output feedback dynamic positioning of surface ships[J]. Journal of Marine Science and Application, 2011, 3(9): 325-332.
[14] 张国银,杨智,谭洪舟. 一类非线性系统非切换解析模型预测控制方法研究[J]. 自动化学报,2008,34(9): 1147-1156.
ZHANG Guoyin, YANG Zhi, TAN Hongzhou. Research on non-switch analytic nonlinear model predictive control method for a class of nonlinear systems[J]. Acta Automatic Sinica, 2008, 34(9): 1147-1156.
