土石料双屈服面弹塑性模型的二次开发算法与应用

岑威钧, 陈司宁, 邓同春, 熊 堃

(1.河海大学水利水电学院, 江苏 南京 210098; 2. 水利部岩土力学与工程重点实验室, 湖北 武汉 430010; 3. 长江勘测规划设计研究有限责任公司, 湖北 武汉 430010)

ADINA、ABAQUS和ANSYS等大型商用有限元软件前后处理方便、计算求解能力高、扩展开发性强,已在岩土工程数值分析领域中得到了较为广泛的应用[1-2].对土石坝结构分析而言,目前商用软件均能方便地实现坝基分期开挖、坝体分期填筑、坝料分区设置及各种接触关系的仿真模拟.然而,这些商用软件的本构库中仅有Mohr-Coulomb模型、Drucker-Prager模型和(修正的)CAM黏土模型等少数岩土材料模型,缺乏我国土石坝工程界广泛应用的Duncan双曲线非线性弹性模型、沈珠江双屈服面弹塑性模型(简称沈珠江模型)等实用土石料本构模型,不适合精细求解土石坝的应力变形问题,特别在高土石坝相关问题研究中受到了较大的应用限制.

所幸这些商用软件都预设了二次开发平台,用户可以根据实际需要添加所需的本构模型:Duncan非线性弹性模型已被开发应用于ABAQUS、ANSYS及ADINA等大型商用软件中[3-5];“南水”模型已被添加到ABAQUS的本构库中[6-7];修正剑桥模型也在ANSYS中进行了二次开发[8].相对于非线性弹性模型的开发,双曲面弹塑性模型的二次开发要复杂许多,涉及到应力的精确更新问题,即本构积分算法,这是弹塑性本构模型二次开发的重点和难点.Wissman[9]和Sloan[10]等较早地提出了次阶应力积分算法,将应变增量细分成很多次阶,在每个次阶中使用欧拉法、改进欧拉法或龙格-库塔法进行积分得到应力增量,然后进行叠加;Borija等[11]提出了隐式回归算法,通过迭代算法使应力状态返回到屈服面上.回归算法又包括常弹性模量回归和变弹性模量回归,Potts等[12]对上述两种应力积分算法做了比较,认为两种算法都能得到准确的结果,但在多屈服面本构开发以及弹性非线性很强的本构模型上,次阶算法更为占优.

为了充分利用商用有限元软件的优势,拓展其在岩土工程领域中的应用范围,本文详细介绍了沈珠江双屈服面弹塑性模型[13]的二次开发流程,对关键的本构积分算法进行了改进和验证,最后进行了工程实例应用.由于ADINA、ABAQUS和ANSYS等软件均用FORTRAN语言进行本构模型的二次开发,且这些软件开发本构模型的思想是相同的,因此文中所述二次开发流程和关键算法同样可用于上述商用有限元软件中开发双屈服面或多屈服面弹塑性本构模型时提供参考.

1 沈珠江双屈服面弹塑性模型

沈珠江双屈服面弹塑性模型[13-14]的屈服面由椭圆曲线和幂曲线组成,其定义的屈服函数为

(1)

式中:

p和τ8分别为八面体正应力和剪应力;

t和s分别为椭圆和幂函数的屈服面系数,不同的土石料t和s取值不同,对细粒土建议t=2,s=3,对堆石料等粗粒土建议t=s=2.

根据经典弹塑性理论,总应变可分解为弹性和塑性两部分.对于双屈服面模型,塑性应变增量由两部分组成,各自对应一个屈服面.采用正交流动法则,则应变增量可写为

(2)

式中:

A1和A2分别为对应于屈服面函数f1和f2的塑性系数,由常规三轴试验确定;

σij为应力张量分量;

Δεe,ij为弹性应变增量;

Δf1和Δf2分别为f1和f2的增量.

按照正交流动法则,沈珠江模型的塑性系数A1和A2反映了两个屈服面各自产生的塑性应变大小,即塑性势面法向增量,均应非负值.在用常规三轴试验确定A1和A2时,其应力比值始终位于两屈服面法向量之间,可确保A1和A2的非负性[13].在土石坝的施工和蓄水过程中,目前的研究大多认为坝内应力更符合等应力比路径.有限元模拟计算发现坝体某些部位土体单元的应力路径会在两屈服面法向量所围区域之外,导致A1和(或)A2出现负数的不合理现象.为此,在计算程序中需人为限制塑性系数A1和A2的非负性.

设屈服函数f1和f2的历史最大值分别为f1 max和f2 max,则加载准则按如下定义:(1) 当f1>f1 max且f2>f2 max时,为全加载,此时A1>0、A2>0;(2)f1≤f1 max且f2≤f2 max时,为全卸载,此时A1=0、A2=0;(3) 当f1≤f1 max、f2>f2 max或f2≤f2 max、f1>f1 max时,为部分加载,相应有A1=0、A2>0或A1>0、A2=0.沈珠江模型共有黏聚力c、内摩擦角φ、破坏比Rf、弹性模量基数KE、回弹模量基数Kur、模量指数nk、围压为一个大气压时的最大体应变cd、最大体应变随围压变化的幂次nd和最大体应变发生时的应力差与偏应力渐近值的比值Rd等 9个材料参数.

2 二次开发子程序关键算法

开发弹塑性本构模型时的关键问题是选择合适的应力积分算法.本文对常用的基本和中点刚度应力积分算法中应力比例因子ri的求解进行修正改进,同时还采用了Sloan提出的带误差控制的修正向后Euler返回算法[10]进行比较分析.

(1) 计算弹性预测应力.在第n步应力σn已知的情况下,按虎克定律弹性预测第n+1步的试探应力σtrial,n+1.

σtrial,n+1=σn+DeΔεn+1,

(3)

式中:

De为弹性刚度矩阵;

Δεn+1为第n+1步的应变增量.

(2) 判断屈服条件.若弹性试探应力σtrial,n+1均不满足两个屈服条件ftrial,i(σtrial,n+1)>fi,max,说明应力处于弹性状态,无需修正,转到第(6)步直接进行下一荷载步计算;除试探应力σtrial,n+1在两个屈服面内的情况以外,其余3种情况表明试探应力至少“穿越”了一个屈服面,需要进行应力修正.

(3) 计算修正应力.当试探应力“穿越”屈服面时,需要进行应力修正,先按线性假设计算各屈服面的弹性应力比例因子ri为

(4)

式中:

fi(σn)为时刻n所对应的屈服函数值,若σn位于该时刻的屈服面上则为0,反之为负数;

ftrial,i为弹性试探应力对应的屈服函数值,i=1,2分别对应双屈服面模型的体积屈服面和剪切屈服面.

对于双屈服面弹塑性模型,按线性假设求得弹性应力比例因子ri可能会有较大误差,因此需要按式(5)重新计算,直至相邻rk,i和rk+1,i之差小于允许值为止.

rk+1,i=rk,i-

(5)

式中:

Δσ为应力增量;

r0,i=0,r1,i=1.

弹性比例因子ri做上述迭代修正后发现算法更准确有效.

令α=rk+1,i,则应力增量αΔσtrail,n+1为弹性分量,应力增量(1-α)Δσtrail,n+1为塑性分量.修正应力Δσ0只根据塑性阶段计算.

Δσ0=(1-α)Δσtrail,n+1-Dep(1-α)Δε=

(1-α)(Δσtrail,n+1-DepΔε).

(6)

由式(3)和式(6)可得

Δσn+1=Δσtrail,n+1-Δσ0=

αΔσtrail,n+1+Dep(1-α)Δε=

(De-(1-α)Dp)Δε,

(7)

式(6)、(7)中:

Δε为应变增量;

α为对应“穿越”屈服面的修正系数;

Dep为σn对应的弹塑性矩阵;

Dp为塑性矩阵.单屈服面穿越的情况下,另一个屈服面的塑性系数为0.

由式(7)可知,在求第n+1级应力增量时,应力应变矩阵相当于在弹塑性矩阵Dep计算中将塑性部分乘以“塑性比例因子”(1-α).当试探应力同时“穿越”两个屈服面,只需令α=(rk+1,1+rk+1,2)/2即可.

(4) 更新应力.若采用基本刚度法时,则更新后的第n+1级应力σn+1为

σn+1=σn+Δσn+1.

(8)

为了增加计算精度,可采用中点刚度法对第n+1级应力σn+1进行2次计算,“中点”应力可按式(9)计算,取塑性应力增量的中点值为

(9)

上述两种常规应力积分算法在程序代码编写时不进行误差控制,随着荷载步的增加其应力应变会越发偏离真值,只有在荷载步足够小时满足计算精度要求.对于荷载步较大情况,建议使用带误差控制的改进Euler积分算法.该法是一种子步应力积分算法,其核心思想就是按照应力误差对第n+1级应变增量步长进行动态调整,即上述计算中Δεn+1用βkΔεn+1替代,其中调整系数βk满足0<βk≤1和∑βk=1,k为子步数.按式(10)计算第n+1级应力计算时的迭代误差.

(10)

式中:

Δσk-1,n+1、Δσk,n+1分别为时刻n+1第k-1和k子步的应力增量.

如果计算得到的应力误差Err大于控制值Eps(一般可取10-3),则采用Sloan的建议对βk按式(11)进行更新.

(11)

继续迭代计算至满足误差结束为止.最终要求在第n+1级下满足应力误差的各次迭代计算的βk之和为1,这样完成了该级的应力增量更新计算,转入到下一步.

(5) 计算弹塑性矩阵.根据更新后的应力σn+1和式(3)计算第n+1级弹塑性矩阵Dep.

(6) 重复上述过程,直至荷载施加完成.

3 算法验证与应用

3.1 算例1——三轴试验

采用雅砻江水电站粗粒土的三轴试验资料[7],进行固结排水剪切试验的数值模拟,试验采用应力控制式,围压分别按0.5、1.0、2.0 MPa三级进行.

图1为试验数据及数值模拟结果,其中:σ1-σ3为主应力差;εa为轴向应变;εV为体积应变.限于篇幅,文中仅给出了围压1 MPa和2 MPa 时3种不同应力更新算法的计算曲线.由图1可见,不同应力积分算法得到的数值模拟曲线与原试验曲线均吻合程度有所不同,其中以带误差控制的改进Euler积分算法最优.

(a) (σ1-σ3)-εa曲线(b) εV-εa曲线(c) (σ1-σ3)-εa曲线(d) εV-εa曲线图1 三轴试验数值模拟结果Fig.1 Numerical simulation results of triaxial test

3.2 算例2——模型面板坝的应力变形

本算例为100 m高的模型面板堆石坝,上下游坡坡比均为 1∶1.4,大坝堆石料计算参数见文献[14].利用本文算法在ADINA中二次开发程序计算得到的大坝应力变形分布规律与文献[14]中相应结果一致,限于篇幅,未给出等值线图,其中各物理量极值对比见表1.

除坝体向下游水平位移和面板拉应力极值与文献结果有一定出入外,坝体沉降、坝体大主应力和面板挠度极值两者均很接近,且各物理量极值所在位置完全一致.由此验证本文所用算法及编程过程是精确可靠的.

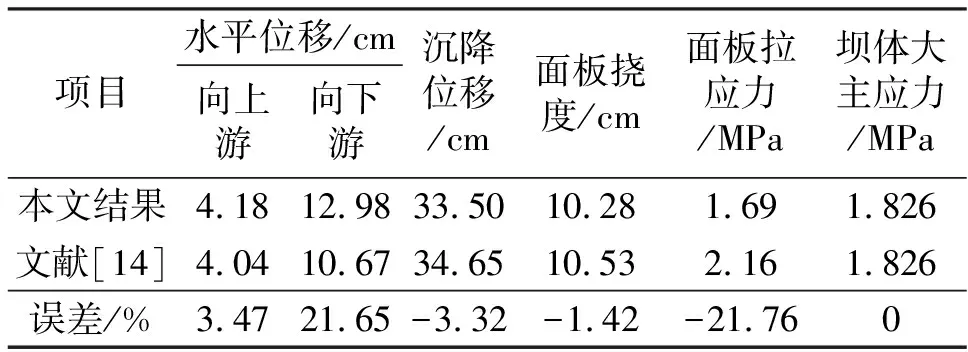
表1 蓄水期大坝各物理量极值对比Tab.1 Extreme-value comparison at water-impounding stage

3.3 工程应用

某混凝土面板堆石坝的最大坝高为132.5 m,上游坝坡坡比为 1∶1.4,下游平均坝坡坡比为 1∶1.57,混凝土趾板置于弱风化基岩上,基岩采用水泥灌浆固结,基础防渗采用灌浆帷幕.大坝典型剖面图见图2,有限元计算网格见图3,其中结点数为 8 126个,单元数为7 199个.坝体及覆盖层计算参数见表2,计算中趾板及面板采用C25混凝土,弹性模量E=28 GPa, 泊松比μ=0.167.

根据图2所示的大坝设计断面,结合坝体填筑及面板分期浇筑施工进程,大坝计算分20级加载模拟.第1级模拟坝基、覆盖层及趾板浇筑,第2～9级为1期坝体填筑,第10级模拟1期混凝土面板浇筑,第11～18级模拟2期坝体填筑,第19级为2期面板浇筑,第20级模拟水库蓄水,蓄水高程为136.04 m.

图2 大坝典型剖面图Fig.2 Typical dam section

图3 有限元计算模型Fig.3 Finite element model

竣工期坝体向上、下游的水平位移极值分别为23.1 cm和19.1 cm,沉降极值为90.9 cm,沉降率为0.686%.图4为蓄水期坝体及覆盖层变形等值线图,大坝变形等值线主要在上游发生变化,向上游的水平位移极值减小至14.1 cm,向下游增至20.6 cm,大坝沉降极值增至91.8 cm,这些数值符合采用沈珠江模型得到的计算结果的一般规律.

表2 坝体及覆盖层沈珠江模型计算参数Tab.2 Constitutive material parameters

竣工期坝体大、小主应力极值分别为2.10 MPa和1.12 MPa,蓄水期坝体大、小主应力极值增至2.21 MPa和 1.17 MPa.图5为蓄水期混凝土面板变形等值线分布图,面板在坝体变形和自身重力的影响下由两岸朝河床中央变形.竣工期面板坝轴向变形主要集中在1期面板上,左右岸变形极值分别为1.46 cm和1.24 cm;沉降和挠度极值位于以1、2期面板交接线的河床中心线附近,分别为7.55 cm 和8.55 cm(凸向上游).蓄水后,顺河向位移、沉降和挠度极值分别增大,轴向变形极值向坝顶方向移动,大致位于两岸坝坡1、2期面板交接处,左右岸变形极值分别为2.79 cm和2.64 cm;沉降极值增至20.2 cm;在库水的作用下,挠度极值向趾板方向移动,大致位于2期面板中心处,其值为21.0 cm(凹向下游).整个面板无论是在竣工期还是在蓄水期,其变形情况均较好地反映了混凝土面板堆石坝面板的工作特性[15].

(a) 顺河向

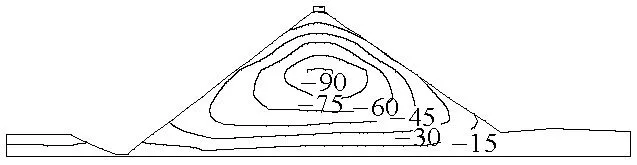
(b) 竖向图4 蓄水期坝体及覆盖层变形等值线(单位:cm)Fig.4 Deformation isoline of dam body and overburden at water-impounding stage (unit: cm)

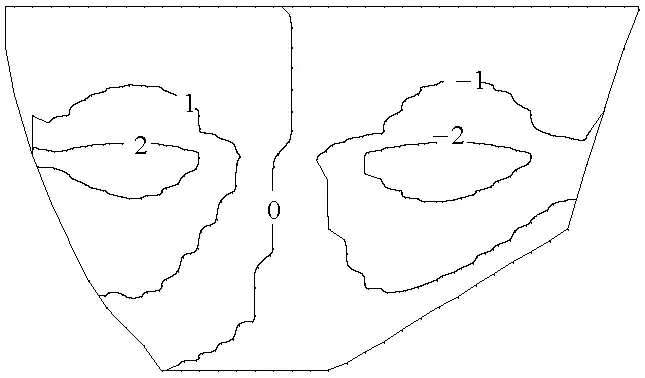
(a) 坝轴向

(b) 挠度图5 蓄水期面板变形等值线(单位:cm)Fig.5 Deformation isoline of concrete slab at water-impounding stage (unit: cm)

图6为蓄水期混凝土面板应力等值线分布图.蓄水后,面板顺坡向应力基本以受压为主,极值为5.38 MPa,右岸2期面板顶部小范围内出现微小拉应力,其极值为0.33 MPa.面板坝轴向应力呈河床中央部位受压、两岸部位受拉的特点,中部应力极值为3.81 MPa,两岸局部区域(大致位于左右岸1、2期面板交界处)出现拉应力,极值为 1.79 MPa.无论是顺坡向还是坝轴向,其面板拉、压应力都分别小于C25混凝土的抗拉和抗压强度.由于面板垂直缝采用了薄层单元模拟,面板应力与变形等值线的光滑程度有一定影响.

面板周边缝和垂直缝的三向变形规律及极值符合面板坝变形基本规律,限于篇幅不再给出接缝三向变形的分布规律图.总体而言,坝体和面板及接缝的受力变形均符合弹塑性坝体材料下的基本特性,各物理量的分布规律和极值也较合理,说明经上述验证的二次开发代码用于预测实际土石坝工程的应力变形是可行和可靠的.

(a) 顺坡向

(b) 坝轴向图6 蓄水期混凝土面板应力等值线分布(单位:MPa)Fig.6 Stress isoline of concrete slab at water-impounding stage (unit: MPa)

4 结束语

土石料本构模型的合理选择很大程度上决定了岩土工程应力变形数值模拟过程的准确性.本文采用应力积分中的基本增量法、中点增量法以及带误差控制的修正向后Euler返回算法,详细介绍了将沈珠江双屈服面模型集成到大型通用有限元软件的本构库中的具体开发流程,拓宽了ADINA、ABAQUS和ANSYS等大型商用有限元软件的应用范围.文中所述二次开发算法同样可供用户开发多屈服面弹塑性本构模型时参考,主体内容和核心代码是相似的,仅在屈服区域判断上稍有不同.

致谢:长江科学院开放研究基金资助项目(CKWV2016376/KY); 水利部土石坝破坏机理与防控技术重点实验室开放研究基金(YK914019).

[1] 熊堃,岑威钧,胡清义,等. 多途径综合开发商业软件精细求解土石坝结构静动力反应[J]. 岩石力学与工程学报,2013,32(1): 117-125.

XIONG Kun, CEN Weijun, HU Qingyi, et al. Static and dynamic response analysis of earth rockfill dams with united multipath development of commercial softwares[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 117-125.

[2] LIU Changhong, LIU Xiaoling, CHEN Qiu. Interval analysis of the finite element method for stochastic structures[J]. Journal of Southwest Jiaotong University, 2001, 12(1): 46-48.

[3] 熊玉春,房营光. ADINA有限元软件中材料本构的二次开发[J]. 岩土力学,2008,29(8): 2221-2225.

XIONG Yuchun, FANG Yingguang. Secondary development of material constitutive model in ADINA software[J]. Rock and Soil Mechanics, 2008, 29(8): 2221-2225.

[4] 江守燕,谢庆明,杜成斌. 基于ABAQUS平台的邓肯-张E-B和E-v模型程序开发[J]. 河海大学学报:自然科学版,2011,39(1): 61-65.

JIANG Shouyan, XIE Qingming, DU Chengbin. Development of program of Duncan-Chang E-B and E-v models based on ABAQUS[J]. Journal of Hohai University: Natural Sciences, 2011, 39(1): 61-65.

[5] 孙明权,陈姣姣,刘运红. 邓肯-张E-B模型的ANSYS二次开发及应用[J]. 华北水利水电学院学报,2013,34(2): 30-34.

SUN Mingquan, CHEN Jiaojiao, LIU Yunhong. The second development of Duncan-Chang E-B model in ANSYS and its application[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2013, 34(2): 30-34.

[6] 岑威钧,朱岳明. 基于 ABAQUS 的土石料本构模型二次开发及其应用[J]. 水利水电科技进展,2005,25(6): 78-81.

CEN Weijun, ZHU Yueming. ABAQUS-based secondary development of constitutive model for earth rockfill materials and its application[J]. Advances in Science and Technology of Water Resources, 2005, 25(6): 78-81.

[7] 司海宝,化西婷. 南水模型在ABAQUS中的实现及在工程中的应用[J]. 南水北调与水利科技,2010,8(1): 52-55.

SI Haibao, HUA Xiting. Development of NHRI constitutive model in ABAQUS and application in engineering[J]. South-to-North Water Transfers and Water Science & Technology, 2010, 8(1): 52-55.

[8] 关云飞,高 峰,赵维炳,等. ANSYS软件中修正剑桥模型的二次开发[J]. 岩土力学,2010,31(3): 976-980.

GUAN Yunfei, GAO Feng, ZHAO Weibing, et al. Secondary development of modified Cambridge model in ANSYS software[J]. Rock and Soil Mechanics, 2010, 31(3): 976-980.

[9] WISSMAN J W, HAUCK C. Efficient elasto-plastic finite element analysis with higher order stress point algorithms[J]. Computers & Structures, 1983, 17(1): 89-95.

[10] SLOAN S W, ABBO A J. Biot consolidation analysis with automatic time stepping and error control. part Ⅰ: theory[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23: 467-492.

[11] BORIJA R I, LEE S R. Cam clay plasticity, part Ⅰ: implicit integration of constitutive relations[J]. Computer Methods in Applied Mechanics and Engineering, 1990, 78(1): 49-72.

[12] POTTS D, GANENDRA D. An evaluation of substepping and implicit stress point algorithms[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 119(3): 341-354.

[13] 沈珠江. 土体应力应变分析的一种新模型[C]∥第五届全国土力学及基础工程学术会议论文选集.北京:中国建筑工业出版社,1990.

[14] 冀春楼. 深厚覆盖层上高堆石坝静、动力分析方法的研究-冶勒堆石坝静、动工作性态研究[D]. 南京:河海大学,1995.

[15] CEN Weijun, WEN Langshen, ZHANG Ziqi, et al. Numerical simulation on seismic damage and cracking of concrete slab for high concrete face rockfill dams[J]. Water Science and Engineering, 2016, 9(3): 205-211.