大功率整流装置谐波治理中的C型滤波器

汪 力，刘忏斌

（1.沈阳市热力工程设计研究院，辽宁 沈阳 110001；2.沈阳铝镁设计研究院辽宁 沈阳 110001）

在大功率整流装置的谐波治理时，多采用各种无源滤波器。在确定滤波器回路内的电器参数时，通常都是与无功补偿容量结合一起考虑。在大容量等效多相系统内，高次谐波的滤除成为了重点，C型滤波器具有良好的高通性能，常用以取代普通高通滤波器，以节省后者中电阻R内的有功损耗，而且通过参数优化，其高通性能可比普通高通滤波器更加优越。

1 电路的构成及其特性

电路图见图1，由电感L，电容C、C1电阻R联结而成，这个电路的关键在于，将L与C1构成在基波频率下的串联谐振环节，从而使基波电流不致流过电阻R，以降低其中的电能损耗。电路的阻抗频率特性见图2。与高通滤波器类似，也应是在截止谐次N1下，回路阻抗有最小值，高于N1时，阻抗应尽可能慢地增加，以便在将截止谐次N1的谐波电流较多地滤除的同时，也能较多地滤除高于N1的各次电流。

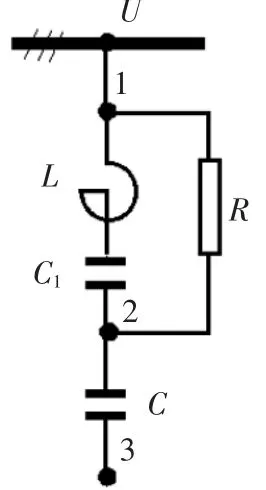
图1 电路原理图

图2 电路的阻抗频率特性

2 电路参数的确定

2.1 电路的阻抗表达式

（1）电路图1中的1点与2点间计入频率（谐次N）变化时的阻抗（略去L的内阻），并引入本电路的前提特征，即基波频率下有：

按图1电路计及（1）式表达的前提，可导出1点与2点间的阻抗：

由（2）式可看出，在基波频率（N=1）下，Z12=0。

（2）电路图1中的1点与3点间计入频率（谐次N）变化时的阻抗（略去L的内阻）

式（3）是绘制电路阻抗频率（谐次）特性Z13=f（N）的依据。

2.2 电感L的计算

由于电路的调谐谐次为N1，因此在N1谐次时有：

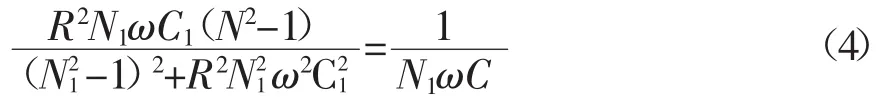
计入在基波频率（N=1）下有：

代入（4）式，求解，可得：

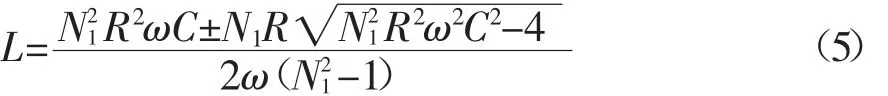
可知，只有在确定电容C和电阻R后，才能计算电感L。

2.3 电容C的确定

由于电容器只能补偿系统的基波无功功率，因此，通常是按系统功率因数所需基波无功的补偿值确定所需电容（C）的数值，应予注意的是电容C1对无功补偿不起作用，所以：

式中：Q1—功率因数补偿所需无功功率，kvar；U—滤波装置接入点的母线线电压，kV；ω—系统的基波角频 ω=2πf，f为基波频率。

2.4 C1的确定

由于L与C1须在基波频率下（N=1）构成串联谐振环节，故可从（1）式导出：

按（5）式确定L后，即可计算出C1。

2.5 电路的品质因数Q及电阻R的确定

当滤波回路在截止频率（对应谐次N1）下产生谐振时，根据谐振电路品质因数Q的定义，其值应为（2）式中感性或容性虚部阻抗与实部阻抗之比，即：

可知：

用（9）式代入（4）式，化简后可得：

根据经验，Q值常在0.5～1.0范围内选取，应予指出：Q值对电路的频率特性影响颇大，往往须在频率特性计算中反复调整，直到得出满意的频率特性为止。于是根据Q的取值和按（6）式求得的C值，即可按（10）式求出电阻R，然后可按（7）式算出所须电容C1。

3 计算举例

3.1 电路基本参数

某电解铝厂变流装置，采用220 kV直降变流机组4套，单组脉动数为12，构成等效48相变流系统。按系统功率因数要求，须装设60000 kvar的补偿电容器，拟在220 kV母线直接接入一组C型滤波补偿装置。试计算其初步所需基本参数。

电容C按（4）式：

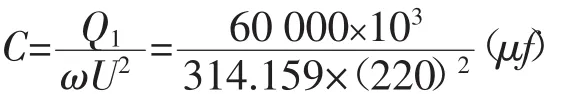
电阻R按（9）式，Q值初步取为0.9，N1取值11得：

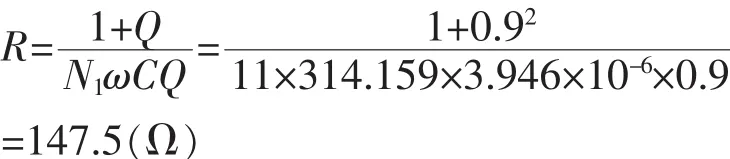
电容 C1按（7）式：

电感L按（10）式：

为比较品质因数对基本参数的影响，对Q=0.5及Q=1.5时也进行了计算，并将3个不同Q值的计算结果按方案一（Q=1.5）、方案二（Q=0.9）和方案三（Q=0.5）列出表 1。

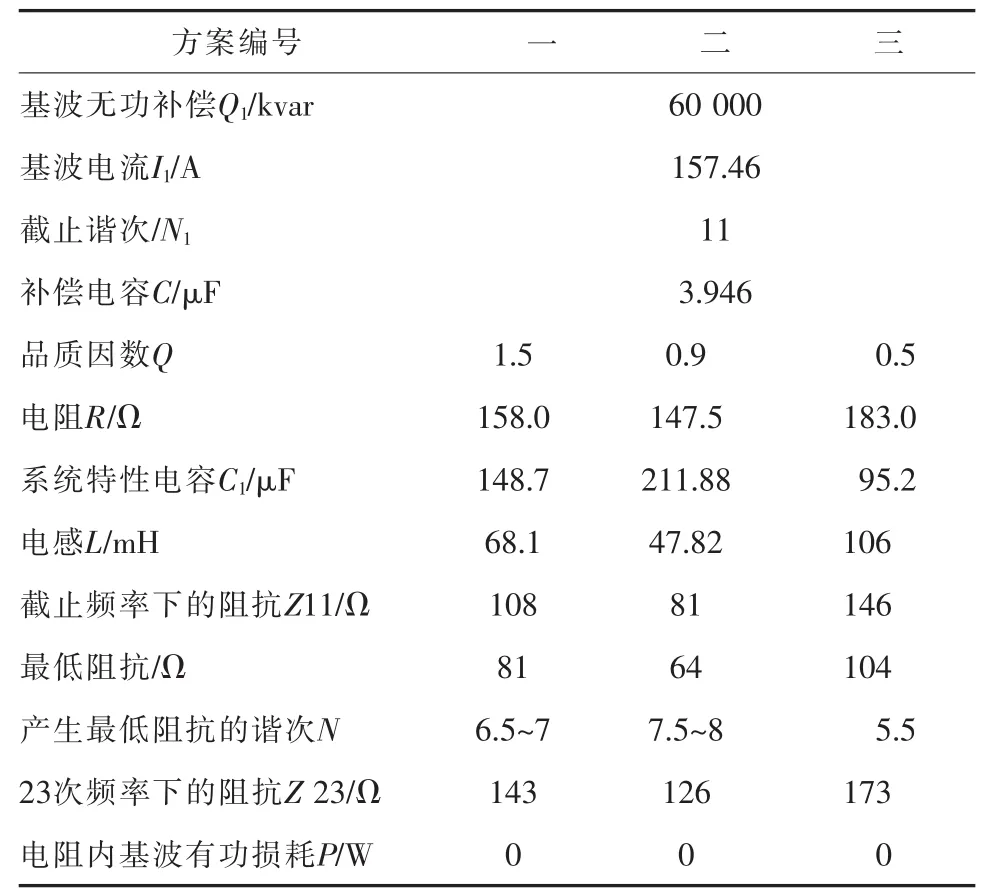
表1 不同方案计算结果

从表列结果看出，品质因数Q对滤波性能影响颇大，比较表列3种Q值的计算结果，以Q=0.9（方案二）为最佳，因为其在截止频率（11次）下的阻抗（Z11）和高次谐波（例如 23次）下的阻抗（Z23）相对最小，说明所希望滤除的截止频率和高次频率谐波滤除量最多；其次为方案一，方案三最差，其截止频率下的谐波电流滤除量最少。品质因数的增减与滤波效果的好坏也非正相关，其最终取值应结合系统的频率特性和各项谐波参数的计算，进行综合评价后确定。

3.2 频率特性

为便于比较，将上述3种品质因数计算的频率特性曲线分别列出。

（1）品质因数Q=0.9时的频率特性曲线，按（3）式计算的全阻抗频率特性见图3。

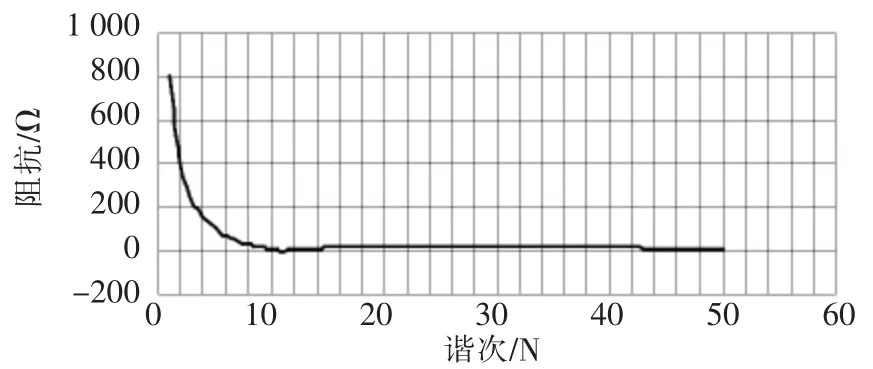
图3 频率特性（Q=0.9）

（2）品质因数Q=0.5时的频率特性曲线，按（3）式计算的全阻抗频率特性见图4。

（3）品质因数Q=1.5时的频率特性曲线，按（3）式计算的全阻抗频率特性见图5。

图4 频率特性（Q=0.5）

图5 频率特性（Q=1.5）

在比较列出的3种不同品质因素Q的阻抗频率特性时，最应该关注的是截止频率下阻抗值小者为佳，高于截止频率下的阻抗值同样以小者为佳，因为这样才能保证滤除的谐波量最多。据此，显然能得出以Q=0.9时滤波效果最好的结论。

4 结语

从本例的计算分析中已可得出，Q=0.9时（图3）为最佳选择，从其电路的频率特性曲线看出，在调谐谐次N1=11次时，阻抗为零，高于11次时阻抗数值并不大，结果比较理想。而Q=0.5（图4）和Q=0.9（图5）电路的频率特性中看出；调谐谐次下的阻抗并非最小，调谐谐次前移至7.5～8次，而不是设计要求的11次，而且高于调谐谐次的阻抗也增加较多，从而影响要求滤除的11次及高于11次谐波的滤除效果。

按（4），（7），（9），（10）式确定了滤波器的基本参数后，下一步须将滤波器与供电系统及谐波源的阻抗参数组成联合系统，进行谐波参数计算，并对滤波效果予以评价，必要时对滤波器参数进行调整后重新计算，以获取滤波各元件的电流、电压、容量、损耗等运行参数，以便提出各元件的订货条件，进行滤波装置的施工图设计。