有砟高速铁路平面优化拟合技术的研究及应用
2018-06-01孙和金
孙和金
(云贵铁路广西有限责任公司,工程师,广西 南宁 530029)
有砟高速铁路具有列车运行速度高及密度大等特点,但轨道平面位置经过高速列车冲击后,原有的轨道线形将发生变化,尤其是曲线部分,线路的总体平顺性受到影响,由于线路平顺性直接影响列车运行的安全性和舒适性,因此,有砟高速铁路维修工作需要精确的作业数据作指导,准确地确定线路平面技术参数,恢复线路的整体平顺性。高速铁路在建设期布设了精准的轨道测量控制网,可用于轨道中线平面坐标测量及平面偏移量测量,测量精度较高,但因受作业条件限制,线路平面拨道量需要通过优化拟合处理取得最优值。为此,研究如何采用线路平面坐标数据或偏差数据拟合计算最佳拨道量,具有十分重要的现实意义。
1 轨道坐标或绝对偏差数据采集
目前有砟高速铁路中线平面坐标及平面偏移量采集均使用线路两侧布设的CPⅢ为控制点,利用轨道测量小车建站后采集平面坐标或平面偏移量,采集的平面坐标为CPⅢ控制网坐标系下的统一坐标,平面偏移量为实测坐标与原设计线位之间的偏差量,数据采集流程如下:
1.1 自由设站用三脚架将智能全站仪架设于距测量起点(或终点)约120m~150m范围内的道心任意位置,棱镜安装在轨道测量小车上,一般情况下选用5~8个CPⅢ点进行建站。
1.2 建站精度要求为满足数据采集精度要求,一般情况下东坐标、北坐标、高程精度均不大于1 mm,方位角偏差不大于2″,转站搭接误差不大于2 mm,搭接长度不小于10 m。
1.3 数据采集间隔采用普通轨道测量小车采集数据时,一般按照约5 m点间距采集坐标及平面偏差数据;采用惯导快速测量小车采集数据时,按照不大于1 m点间距设置并自动采集坐标及平面偏差数据,以提高线路平面拟合精度。
1.4 曲线切线确定为确保曲线偏角的准确性,直线地段测量长度一般不应短于100 m,枢纽区段当夹直线较短时,相临的两曲线应联测联算,以确保两曲线之间的切线方位角一致。
2 线路平面参数拟合计算原理
2.1 线路平面参数计算线路平面主要由直线和曲线组成,曲线又由缓和曲线和圆曲线组成,设曲线两端直线方程分别为y=k1x+b1和y=k2x+b2,曲线半径为R,始终端缓和曲线长分别为Ls1和Ls2,那么,曲线在整个平面中的位置就可以确定。根据曲线两端的直线方程,即可分别求得它们的交点坐标(xjd,yjd),始终端切线方位角A1和A2,曲线转角a和转向系数i(假设左转i=1,则右转i=-1);根据缓和曲线计算公式及平面几何关系(如图1所示),可分别计算出曲线的其它参数,包括切线长 T1、T2,切垂距m1、m2,内移距P1、P2,缓和曲线角β1、β2,外距E、圆心坐标(xo,yo)、曲线五大桩坐标及其方位角和里程等。以上直线、曲线要素及其参数的计算,相关文献及教科书中均有详细的计算公式推导过程及说明,本文不再推导证明。
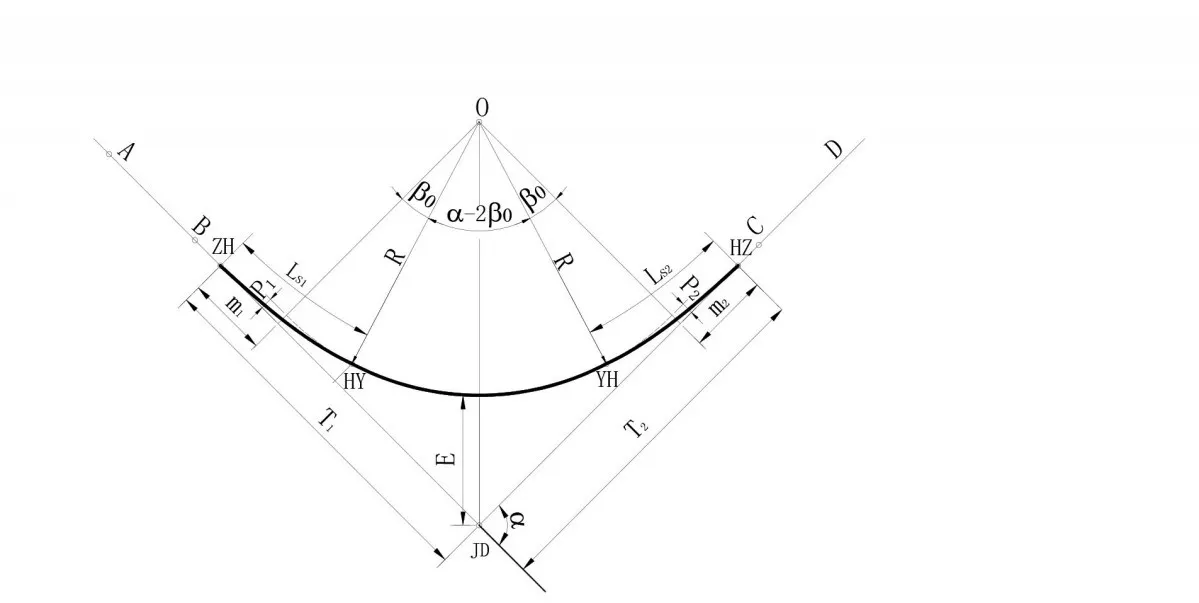
图1 线路曲线要素计算图
2.2 测点性质判断各测点的坐标和偏移量在直线段、缓和曲线段和圆曲线段采用不同的计算方法,所以,计算前要判断各测点的所在位置。由于高铁线路在测量时是利用布设的精测控制网建设坐标系,并且测量设备中建立有线性坐标数据库,测量过程可直接按照测点里程确定实测点性质。
2.3 任意测点向量定义设P为设计中线外任意实际测点,假设坐标为(x,y),M为设计曲线上任意一点,假设坐标为(xM,yM),M点对应的切线方位角为AM,P点相对于M点的切向量和法向量分别用x'M、y'M表示(如图2所示)。
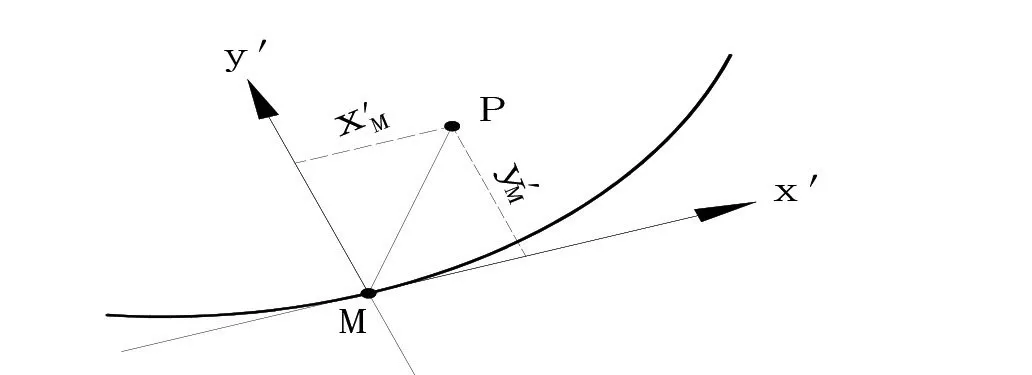
图2 P点相对于M点向量计算图
根据平面几何关系可得:
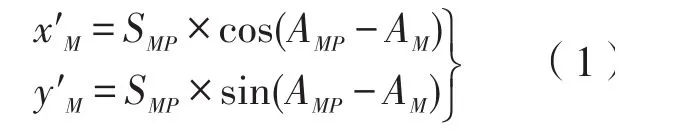
式中SMP为MP直线的距离,AMP为MP直线的方位角。
3 线路拨道量拟合计算原理
3.1 直线段拟合计算直线地段可利用通用方程y=kx+b表示,式中k为斜率,b为y轴上的截距。根据该式,直线方程参数可以分别采用直线上2个实测测点直接确定,也可采用直线上多个测点通过最小二乘法原理拟合确定。
任意测点的拨量等于其相对于ZH或HZ点的法向量y′ZH或y′HZ,即用(2)表示:
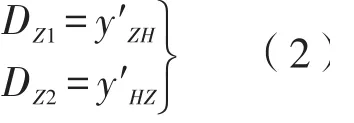
3.2 缓和曲线段拟合计算设P为缓和曲线外任意测点,其直缓点坐标设为(x,y),对应的缓和曲线长设为l(如图3所示),l值可按式(3)迭代计算求得:

式中:n=0,1,2,3,…,初值l0=x
△ln为P点到缓长对应法线的距离,按式(4)计算:
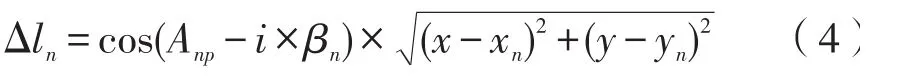
式中:AMP为缓长ln对应的中桩点到P点的方位角i
为转向系数;(xn,yn)和βn分别为缓长ln对应的中线设计坐标和缓和曲线角。当△ln≤0.0001m时停止迭代,这时P点对应的缓长l就等于ln+1。
P点的拨量按式(5)计算:
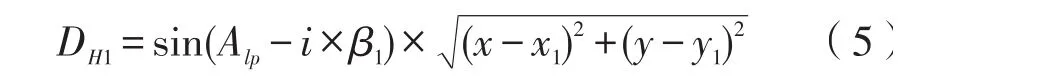
式中:AlP为缓长l对应的中桩点到P点的方位角;(x1,y1)和β1分别为缓长l对应的中桩坐标和缓和曲线角。
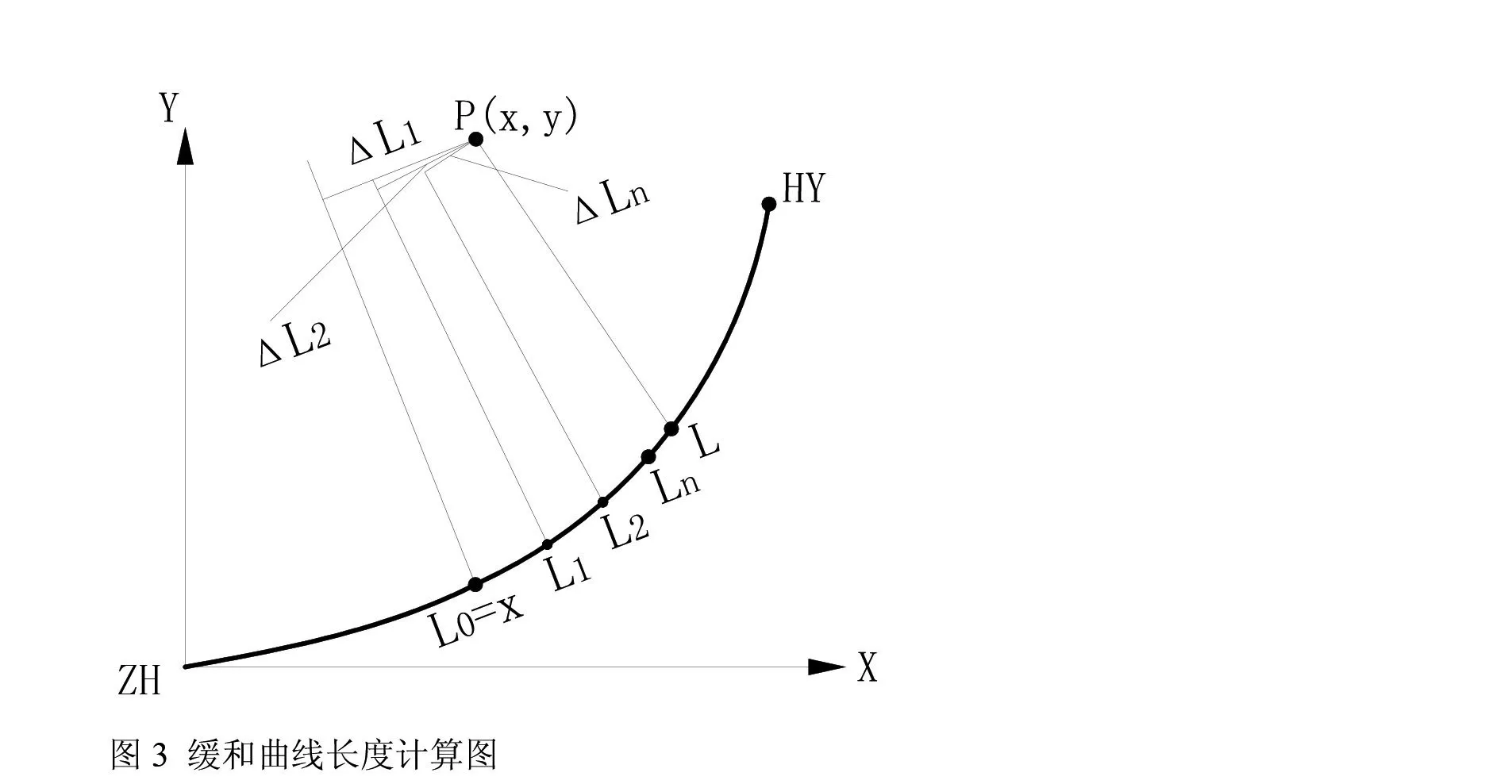
图3 缓和曲线长度计算图
3.3 圆曲线段拟合计算各测点拨量等于圆曲线半径减去测点到圆心点的距离,即用(6)式表示。
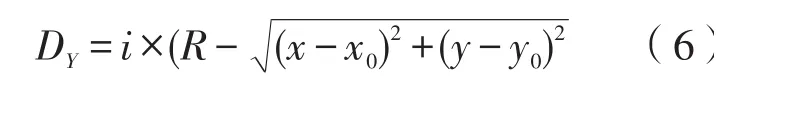
3.4 拨道量正负值确定按顺里程方向当拨量值为正值时表示测点偏离设计中心线左侧,为负值时表示测点偏离设计中心线右侧,当然可根据实际情况自行定义。
3.5 曲线拟合方法本文所研究的坐标或偏差数据整体优化拟合原理为最小二乘法原理,按照曲线的组成,采用半径和缓长分别对应逼近的优化方法,计算出各测点拨量平方和最小时,所对应的曲线半径和缓和曲线长则同为最优,根据高速有砟铁路设计规范,高铁线路主要有缓和曲线长对称优化和已知缓和曲线长优化曲线半径两种形式。
3.5.1 缓和曲线长对称优化 按始终缓和曲线等长进行优化,这时优化参数分别为缓和曲线长和曲线半径。初步给定一个缓长,按照此缓长计算最小拨量平方和及曲线半径,再以初步缓长±10m优化半径求得的最小拨量平方和,计算结果与初步缓长比较,拨量平方和较小时,则继续按+10m或-10m步长递增继续优化,直至最小拨量平方和不再减小为止,最后所得到的缓长、半径及拨道量则为最优。
3.5.2 已知缓和曲线长优化半径 根据给定的缓长对半径进行优选,并使得各测点的拨量平方和最小,这时优化参数为曲线半径。根据原设计缓和曲线长,采用逼近法对半径进行优选,分别计算出各测点的拨量平方和。按照高速铁路线路平面特点,平面曲线半径范围设为400~13000m,分别利用已知缓长计算拨量,并找出拨量平方和为最小时对应的曲线半径,按照此方法循环计算,可确定最优曲线半径及最优拨道量。
4 应用实例
本文选择某有砟高铁线路的一条完整曲线优化拟合为例,曲线参数及拨道量优化计算均采用平面绝对坐标数据,根据优化计算结果与实测线路中心绝对偏差进行比较(见图4所示),图中纵坐标为线路中线偏差量(mm),横坐标为线路里程(km)。优化后线路中线偏差如图4中上侧实线(A线)所示,实测线路中线绝对偏差如图4中下侧实线(B线)所示,从图4中可明显看出按照绝对偏差数据进行拨道时,动道作业量较大,并且整条曲线需要向曲线外股拨移,最大拨道量约为28mm(k398+750),整体工作量较大,并且不利于无缝线路道床稳定性。利用优化后的数据进行作业,只需对k398+350~k398+650及k399+150~k399+350两个区段进行拨道作业,最大拨道量约为12mm(k399+280),极大的减少了工作量,并保持道床的稳定性,符合现场实际情况。
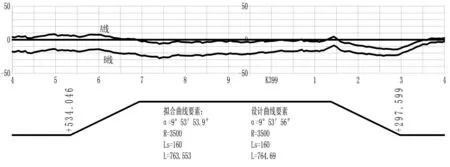
图4 曲线优化拟合数据与绝对偏差比较图
5 结束语
通过有砟高速铁路平面优化拟合的研究及理论计算,线路平面参数及拨道量拟合采用整体优化法,整个曲线及直线上的所有测点坐标均参与拟合计算,确保拟合出最优的平面参数及拨道量,计算结果符合现场实际,满足高速铁路相关技术标准。
综上所述,利用线路平面优化拟合技术,通过现场采集的坐标数据,计算出最接近现场的曲线参数及拨道量,不但可以满足线路平顺性的要求,还可以减少现场作业量,保持道床的整体稳定性,改善列车运行条件。
