一种薄管板简化有限元模型
2018-05-31,,,,,
, , , , ,
(1.甘肃蓝科石化高新装备股份有限公司, 甘肃 兰州 730070;2.上海蓝滨石化设备有限责任公司, 上海 201518;3.中国石油 大连石化公司, 辽宁 大连 116011)
管板是锅壳锅炉和火管锅炉重要的承压元件之一,在使用过程中容易损坏。管板的设计计算方法大致分为两种[1],一种是弹性基础上的当量实心板理论,该理论以等效弹性常数为基础,已经体现在多部国家标准和行业标准当中[2-4]。另一种方法基于光板弯曲理论,是一种简化的计算方法,相关的标准主要有GB/T 16508—2013《锅壳锅炉》[5]和AD 2000 CODE《Technical rules for pressure vessels》[6]等。由于采用光板弯曲理论计算得到的管板厚度很小,因此按照此理论设计的管板通常称为薄管板,对薄管板光板弯曲理论的研究远没有对当量实心板理论研究的深入。光板弯曲理论没有准确的理论基础,但是大量的应用实践,特别是在中低压锅壳锅炉上的应用实践证明这种设计方法是可行的,同时也是安全的。
管板的结构和承载状况均非常复杂,通过传统的方法准确计算管板应力十分困难,一般需要进行有限元应力分析校核。笔者在分析管板受力的基础上,提出了一种薄管板应力计算简化模型,并以1台锅壳锅炉为例,采用两种有限元模型对两种工况下设备薄管板应力进行了分析对比。
1 管板受力分析
一般锅壳锅炉壳程操作压力远高于管程,故用设备承受壳程压力分析管板受力。管板承受壳程压力,会产生壳体轴向的位移和变形。在布管区,换热管与管板为刚性连接,在换热管拉撑作用下,管板变形很小,且应力很低。非布管区的应力则较高,扳边的应力值尤其高,通常为布管区应力值的几倍甚至十几倍,文献[7-8]和工程经验均验证了这一点。
管板非布管区应力高是由于非布管区距离周边支撑点(线)较远,当量圆直径大,在压力载荷作用下,其受力模型为平板受侧向载荷,以弯曲应力为主。
扳边应力高是壳程圆筒、管板和换热管变形协调所致。在压力载荷下,壳程圆筒承受内压,环向应力高,轴向应力很低,轴向应力远不到环向应力的一半。在泊松效应下,壳程圆筒变短。而管板承压后对换热管有拉伸作用,换热管受外压,在泊松效应下有变长的趋势。换热管在外压和管板拉伸作用下变长,而壳程圆筒变短,管板与换热管组成的体系和壳程圆筒在轴向均具有较大的刚度,其变形差由扳边来协调,导致扳边应力远高于其他部位。如不考虑结构中的应力集中,扳边则是结构中产生应力最大部位,是结构设计的重点。
2 管板应力计算简化模型
众多的文献均表明,在管板布管区,在换热管拉撑作用下,管板的应力远低于材料的许用应力,故笔者提出一种简化的管板应力计算有限元模型,不考虑管板布管区的应力水平,假定管板布管区是安全的,只考察扳边、筒体的强度。将载荷对管板、换热管作用产生的位移直接施加到管板布管区,在布管区以外的管板、扳边和筒体上按计算条件施加边界条件。这样可以将管板、管束和壳体简化为轴对称问题,极大降低数据准备工作量、计算机耗用机时和硬盘存储空间。
3 管板应力分析对比
3.1 换热管布管及参数
以1台锅壳锅炉为例,采用两种有限元模型进行应力分析对比。
模型1为本文提出的简化模型,模型2为对设备3D模型结构直接离散化。对结构直接离散是目前的通用做法,其准确性得到业界的肯定,但该方法模型复杂,计算量大,在设备直径大、换热管数量多的情况下尤其如此[9]。
该锅壳锅炉的壳程设计压力为3 MPa,管程设计压力为0.1 MPa,管、壳程设计温度均为150 ℃。采用薄管板结构,换热管规格(直径×壁厚×长度)Ø42 mm×3 mm×2 000 mm,共有336根,呈正三角形排布,管间距54 mm,布管示意见图1。

图1 换热管布管示图
按照文献[5]进行计算,管板的计算厚度不足4 mm。为了满足制造需求,取管板有效厚度12 mm,扳边起点半径550 mm,扳边圆弧内半径40 mm,壳体内径1 180 mm,壳程筒体有效厚度12 mm。换热管材料选用20钢,管板和壳程圆筒的材料均选用Q345R。
3.2 工况及参数选取
考察两种工况下管板的应力,工况1只考虑壳程压力作用而不考虑膨胀差,工况2同时考虑壳程压力和膨胀差的作用。对工况2,取换热管平均温度100 ℃、圆筒平均温度50 ℃、管板平均温度150 ℃、材料导热系数50.2 W/(m·℃)、线膨胀系数11.88×10-6/℃。有限元分析时,在管板平板区施加150 ℃温度载荷,对壳体施加50 ℃温度载荷,对管板扳边则不施加温度载荷,其温度场由壳体与管板平板之间热传导形成。
针对模型1,计算出换热管的轴向膨胀量后,将其作为位移施加到管板的管束作用区域。对模型2,对换热管施加100 ℃温度载荷。
3.3 有限元模型建立
3.3.1模型1
在壳程设计压力的作用下,管板对换热管有拉伸作用,该作用下换热管的变形量Δ1按照式(1)进行计算[10]:
(1)
式中,F为管板对换热管的拉伸力,N;Lt为换热管计算长度,mm;Et为换热管材料的弹性模量,MPa;At为1根换热管截面面积,mm2。
换热管在内外压力作用下因泊松效应引起的轴向变形Δ2为[11]:
Δ2=μσLt/Et
(2)
式中,μ为换热管材料的泊松比;σ为换热管环向应力,其数值按GB 150.3—2011《压力容器 第3部分:设计》[12]计算。
在操作条件下,换热管温度升高的自由膨胀量ΔL为[10]:
ΔL=LtαtTt
(3)
式中,αt为换热管材料的线膨胀系数,℃-1;Tt为换热管操作状态下金属温度与常温的差值,℃。
则施加在管板布管区上的位移ω为:
ω=Δ1+Δ2+ΔL
(4)
模型1采用简化轴对称模型,考虑到结构轴向的对称性,取圆筒长度的一半建立有限元模型。采用ANSYS软件4节点平面单元plane182并设置轴对称选项,共计2 627个节点、2 098个单元。模型1有限元分析模型见图2。
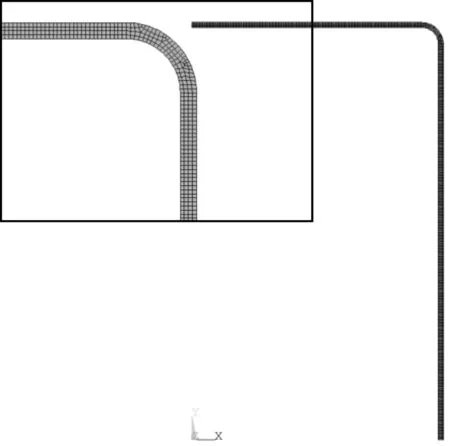
图2 模型1有限元分析模型
工况1下采用式(1)、式(2)和式(4)计算得到管板布管区的轴向位移为0.118 3 mm,在布管限定圆内施加0.113 5 mm的轴向位移,在管板其余位置及壳体内壁施加3 MPa的设计压力,在壳体截断面施加轴向位移约束。将管板当量为等效实心板既要考虑开孔对管板的削弱作用,又要考虑管子的加强作用。前人对孔板有效弹性常数进行了大量研究,文献[4]给出了不同情况下弹性模量和泊松比的折算方式。该方法计算过程复杂,工作量较大。目前我国通常采用的是空间带效率0.2~0.35的管板,相比现行美、英、法等国规范采用值,无论管子与管板的连接方式为焊接还是胀接,管子对管板的加强作用都大得多,故在GB/T 151—2014和JB 4732—1995《压力容器——分析设计标准》[13]中选用刚度削弱系数为0.4。应力分析时管板布管区的弹性模量取管板材料弹性模量的0.4倍,管板扳边和圆筒的弹性模量为材料的实际值。
对工况2采用间接耦合的方式进行分析,首先分析温度场,将温度场分析结果作为载荷与压力载荷一同施加到模型1中,其中管板布管限定圆轴向位移为1.063 9 mm,在壳体截断面施加轴向位移约束。应力分析时管板布管区的弹性模量取管板材料的0.4倍,管板扳边和圆筒的弹性模量为管板材料的实际值。
3.3.2模型2
模型2认为换热管与管板连接采用全焊透结构,并在对称面上施加对称约束[14-18]。考虑结构和载荷的对称性,建立结构的1/8模型,即取管板的1/4区域和换热管长度的一半建立模型。模型中各元件的弹性模量和泊松比取各自材料的实际值,采用8节点三维实体单元solid185,共计261 141个节点、178 256个单元。
模型2有限元分析模型见图3。

图3 模型2有限元分析模型
工况1只考虑压力载荷作用,在管板壳程侧、圆筒内壁和换热管外壁施加3 MPa的计算压力,在模型对称面施加对称约束。
对工况2采用间接耦合的方式进行分析,将温度场分析结果作为载荷与压力载荷一同施加到模型中,在模型对称面施加对称约束。
3.3.3应力计算结果及评定

图4 工况1下模型1应力云图

图5 工况1下模型2应力云图

图6 工况1下模型1温度场分布
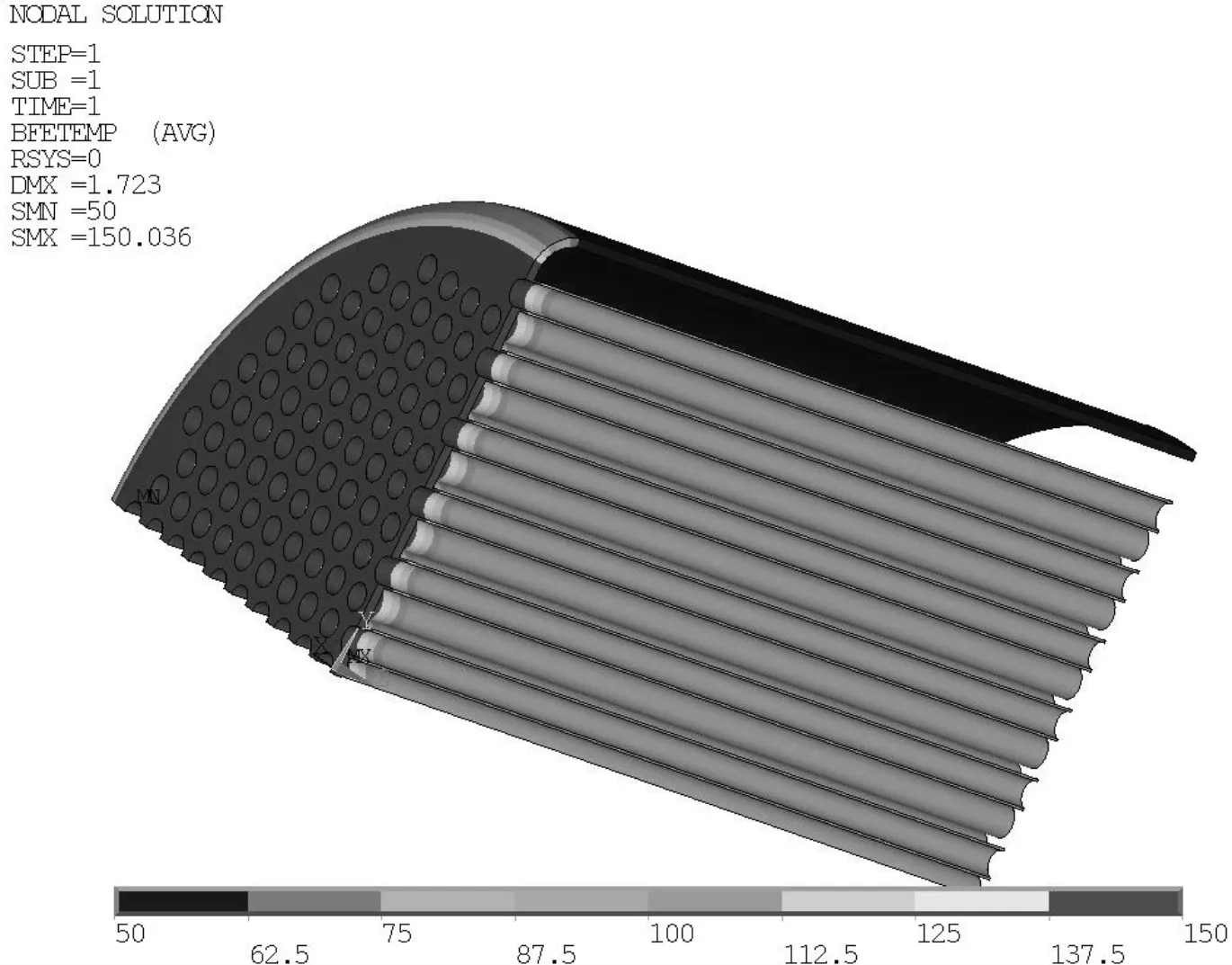
图7 工况1下模型2温度场分布
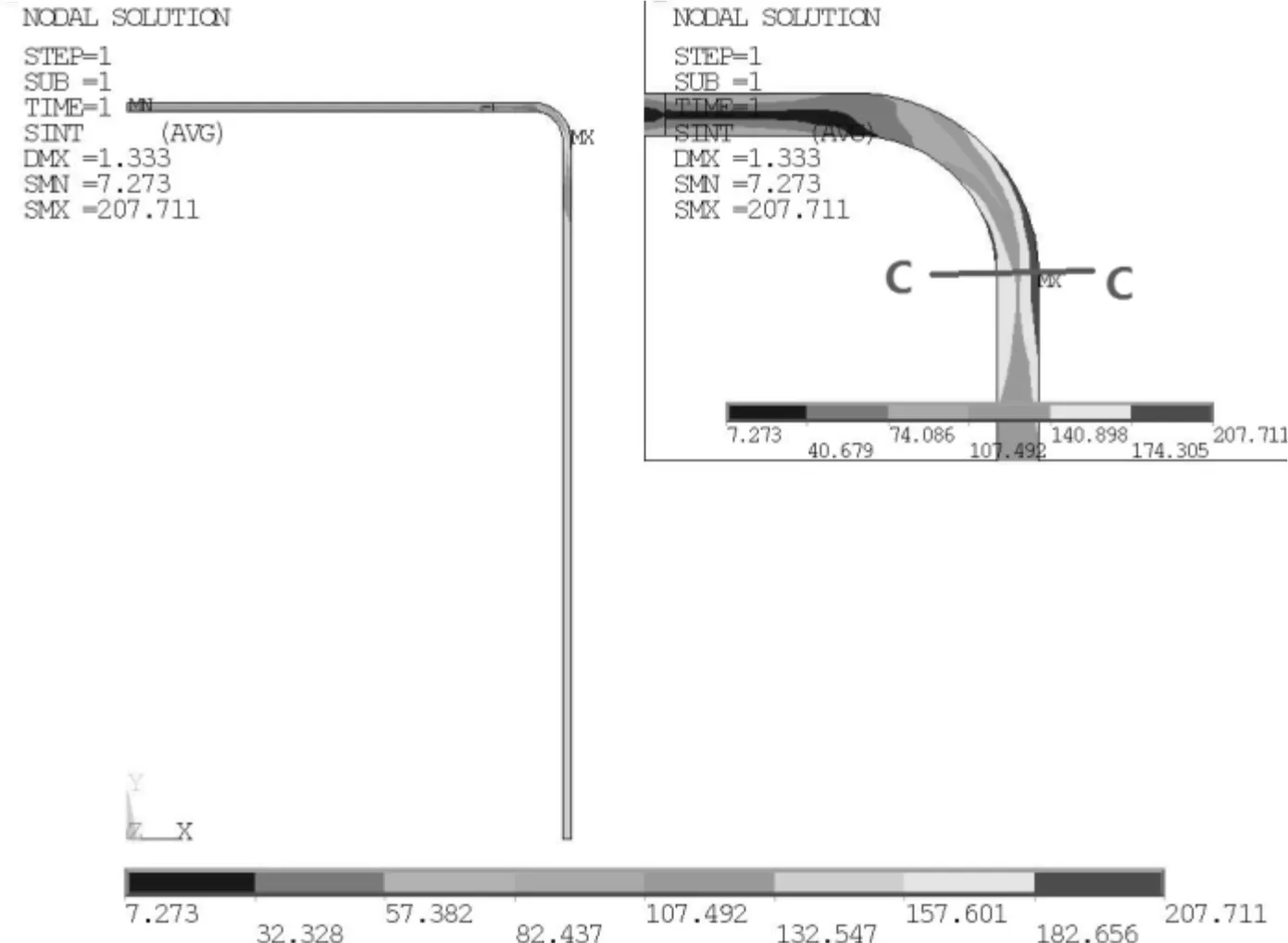
图8 工况2下模型1应力云图

图9 工况2下模型2应力云图
工况1下两种模型应力云图见图4~图5,温度场分布见图6~图7。工况2下两种模型应力云图见图8~图9。由各图可知,两种模型在同种工况下扳边区域的应力分布基本一致。工况1下两种模型的最大应力分别为169.46 MPa和166.935 MPa,差值约为1.5%;工况2下两种模型的最大应力分别为207.1 MPa和202.5 MPa,差值约为2.6%。
在模型1、模型2上分别设置线性化路径A-A、C-C、B-B和D-D,按照文献[13]对各路径的应力进行分类和评定,结果见表1。表1中K为载荷组合系数;Sm为各材料的许用应力,MPa。

表1 不同工况下两种模型应力计算结果及评定
由表1可知,与路径B-B相比,路径A-A的局部薄膜应力小21.5%,一次加二次应力大5.6%;与路径D-D相比,路径C-C的一次加二次应力大7.0%。除局部薄膜应力外,一次加二次应力计算误差在合理范围内。
无论是本算例还是大量的实践经验均表明,在中低压锅炉的评定中,管板扳边处的一次加二次应力是安全制约因素,局部薄膜应力裕量大于一次加二次应力,不是结构的安全制约因素。文中提出的简化模型对结构最大应力的计算与模型2基本相当,且略显保守。
4 结语
通过对设计实例的分析,表明两种模型对结构最大应力的计算结果相差不超过2.6%,可以将文中提出的简化模型作为校核管板扳边应力的一种简捷的方法,用于指导工程实践。
采用该简化模型的计算量远少于模型2,在直径更大、换热管数量更多的设备分析中优势更为明显。但当布管限定圆略有差别时,最外缘布管数量将受到影响,进而影响扳边的应力。此情况下采用该简化模型不如采用三维实体模型那么灵敏,如计算结果强度裕量较小,建议采用其他模型或计算方式进行验证。
参考文献:
[1] 余伟炜,高炳军.ANSYS在机械与化工装备中的应用[M].北京:中国水利水电出版社,2006.
YU W W,GAO B J. The use of ANSYS in machine and chemical industry[M].Beijing:China Water Power Press,2006.
[2] 热交换器:GB/T 151—2014[S].
Heat exchangers:GB/T 151—2014[S].
[3] Standards of tubular exchangers manufacturers association,2007[S].
[4] ASME boiler and pressure vessel code Ⅷ division 1—2013[S].
[5] 锅壳锅炉:GB/T 16508—2013[S].
Shell boilers:GB/T 16508—2013[S].
[6] Technical rules for pressure vessels:AD 2000 CODE[S].
[7] 杨国义,刘玉斌.薄管板换热器强度设计探讨[J].石化技术,1999,6(1):24-26.
YANG G Y,LIU Y B. Strength design study of thin tubesheet heat exchanger[J]. Petrochemical industry technology,1999,6(1):24-26.
[8] 杨国义,李永生.薄管板换热器强度试验研究[J].管道技术与设备,1993(3):9-10.
YANG G Y,LI Y S. Strength experimental study of thin tubesheet[J].Pipeline technique and equipment,1993(3):9-10.
[9] 王泽军.锅炉结构有限元分析[M].北京:化学工业出版社,2005.
WANG Z J.FEA of boiler structure[M].Beijing:Chemical Industry Press,2005.
[10] 范钦珊,殷雅俊,唐靖林.材料力学[M].北京:清华大学出版社,2014.
FAN Q S,YIN Y J,TANG J L. Mechanics of materials[M].Beijing:Tsinghua University Press,2014.
[11] 徐芝纶.弹性力学[M].北京:高等教育出版社,2006.
XU Z L. Elasticity[M].Beijing:Higher Education Press,2006.
[12] 压力容器:GB 150.1~150.4—2011[S].
Pressure vessels:GB 150.1~150.4—2011[S].
[13] 钢制压力容器——分析设计标准:JB 4732—1995[S].
Steel pressure vessels——design by analysis:JB 4732—1995[S].
[14] 杨国义,陈志伟,侍吉清.局部区域布管固定管板热交换器应力的有限元分析[J].石油化工设备,2010,39(2):30-32.
YANG G Y,CHEN Z W,SHI J Q. Stress analysis and evaluation for heat exchanger tubes arranged in local area of tubesheet[J]. Petro-chemical equipment,2010,39(2):30-32.
[15] 张型波,赵国栋,马一鸣.布管方式对管板热应力的影响[J].压力容器,2017,34(9):48-53.
ZHANG X B,ZHAO G D,MA Y M. Effect of tube arrangement on thermal stress of tube sheet[J].Pressure vessel technology,2017,34(9):48-53.
[16] 刘庆刚,刘玻江,朱海荣,等.管壳式热交换器扇环形管板开孔应力集中系数分析[J].石油化工设备,2018,47(1):20-25.
LIU Q G,LIU B J,ZHU H R,et al. Stress concentration factor analysis of openings on an annular sector tube sheets used in a shell and tube heat exchanger[J]. Petro-chemical equipment,2018,47(1):20-25.
[17] 张型波,孙昊,赵明明.一种反向扳边挠性管板的应力分析[J].压力容器,2016,33(7):25-31.
ZHANG X B,SUN H,ZHAO M M. Stress analysis of an reverse-edge fold flexibility tube sheet[J].Pressure vessel technology,2016,33(7):25-31.
[18] 姚兴安,王海峰.钛热交换器胀焊接头胀接残余接触压力模拟计算[J].石油化工设备,2017,46(1):12-19.
YAO X A,WANG H F. Study on residual contact stress for titanium-made heat-exchanger joint made by expansion and welding[J]. Petro-chemical equipment,2017,46(1):12-19.
