牛顿流体圆管内非稳态Poiseuille流动特性
2018-05-31汤苑楠卢兴国
陈 雷, 汤苑楠, 刘 刚, 卢兴国
(1. 中国石油大学(华东)储运与建筑工程学院,山东青岛 266580;2.山东省油气储运安全省级重点实验室,山东青岛 266580; 3.中国石化销售有限公司华南分公司,广东广州 510000)
为保证原油管道的安全经济运行,须全面把握原油管道停输再启动过程,许多学者[1-3]开展了胶凝原油管道测试研究。室内环道是常见测试手段之一,其测量原理是Hagen-Poiseuille流动。在Hagen-Poiseuille流动的初始阶段,必然存在管内流速分布不断变化的非稳态过程,造成测量黏度值与真实黏度值的差异。为明晰相关测试影响因素,减小测试误差,有必要掌握非稳态Poiseuille流动阶段流体表观的测试结果与真实流变性的差异以及不同边界条件对于非稳态流动过程的影响。最经典的非稳态Poiseuille流动为“置有牛顿流体的无限长水平圆管,初始静止,然后突然施加恒定压力,流体开始运动”。Papanastasiou等[4]采用分离变量法给出了恒压力边界条件下圆管内不可压缩非稳态Poiseuille流动的解析解,但并未讨论恒流量条件下的非稳态Poiseuille流动。Bar[5]对两种不可压缩牛顿流体混合物展开研究,得出非定常平板和轴对称Poiseuille流动下的速度分布解析解。Erdogan[6-7]控制恒压力边界条件,对两个无限大平板间以及圆管内牛顿流体的非稳态Poiseuille流动展开研究。Erdogan等[8],研究了牛顿流体和二阶流体的剪切应力随时间变化规律的差异。Siddique等[9]控制与时间有关的剪切应力边界,对不可压缩的广义Oldroyd-B流体进行研究,得到级数形式的速度分布和剪切应力的通用解。Fetecau[10]对几何形状为轴对称的圆管的无边界区域内的Oldroyd-B 流体进行研究。Muzychka等[11]通过寻求非稳态Poiseuille流动和斯托克斯第一问题的关联,建立了描述内表面剪切应力以及速度分布随时间变化的简易模型,并对结果进行了渐近分析。Hayat等[12-13]控制周期性压力边界和恒压力边界,对两平板间不可压缩二阶流体进行研究。此外,还有一些学者采用数值计算的思想展开了相关探究。Vinay等[14]建立了非牛顿流体圆管内非稳态流动的数值计算模型,对方程组进行离散求解。Negrão等[15]考虑了管道径向速度的变化开展研究。但上述学者仅讨论了恒压力边界条件下的非稳态流动过程。目前,关于Poiseuille流动的非稳态过程研究,主要关注流体非稳态速度分布函数的求解,边界条件集中在恒压力边界条件,并未关注不同边界条件下流动过程的差异以及非稳态过程对细管法测试黏度准确性的影响。笔者对不同边界条件下的圆管内非稳态Poiseuille流动过程进行分析,对比边界条件对于非稳态过程的影响。暂不考虑流体本身流变性的变化,选取牛顿流体为研究对象,考虑径向速度分布,采用数值计算方式,以无量纲黏度和无量纲时间为非稳态过程表征量,讨论不同边界条件对非稳态Poiseuille流动过程的影响。
1 问题描述
1.1 细管法黏度测试基础原理
细管法测定液体的流动性广泛应用于各种流体流变性的测量[16]。对于稳定的管道层流,两端压差P恰好提供流体圆柱体在管道内壁上的黏滞力,管壁剪切应力τ与压差Δp之间满足
(1)
式中,L为细管长度,m;R为细管半径,m。
对于牛顿流体与幂律流体的稳定圆管层流,其管壁处剪切速率可表示为
(2)
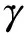
根据式(1)与(2)可获得流体剪切速率与剪切应力的关系,进而确定流体黏度或本构方程。测量黏度的表达式为
(3)
式中,μM为测量黏度,Pa·s。
细管法开展流体测试,必须满足的核心条件是流体应为与时间无关的不可压缩流体,流动状态为充分发展的稳定层流[16]。然而在实际流动过程中,在非稳态Poiseuille流动阶段,管内流体速度不断变化,基于细管法黏度测试原理计算的黏度数值不再是流体真实黏度。有必要明确非稳态Poiseuille流动阶段测试的流体表观流变性与理想均匀剪切条件下流体的真实流变性间的差异,从而探究初始非稳态流动阶段速度分布的发展对细管法测试的初始流变数据的影响。
1.2 表征非稳态过程的无量纲参数定义
1.2.1 无量纲黏度
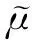
(4)
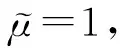
1.2.2 无量纲时间
在利用解析方法进行非稳态流动的相关研究中通常利用无量纲时间描述非稳态流动过程[7],无量纲时间的定义为
(5)

1.3 不同边界条件选取说明
在实际管道非稳态流动测试中恒流量[19]和恒压力[20-21]是最为常用的加载条件。除此之外,在控制流量边界下初期可能存在流量从0线性增加的情况[22]。选取的边界条件分别为恒流量边界、流量从0线性增加边界和恒压力边界。
定义截面上平均速度概念为
(6)
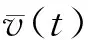
为计算方便所有的恒流量条件转换为恒平均速度边界条件,从0线性增加的流量条件转换为从0线性增加的平均速度边界。三大边界条件为:①恒平均速度边界条件;②从0线性增加的平均速度边界条件;③恒压力边界条件。
2 非稳态Poiseuille流动模型建立
对于不同边界条件下的圆管内Poiseuille流动,如图1所示,取一段管长为L,管径为R的圆管,管道保持水平,管内充满不可压缩牛顿流体。初始状态全线压力、速度均为0。在管道始端突然施加一定的加载条件,流体开始运动。
如图2所示,圆管内空间被划分为n个圆筒微元,i表示微元界面位置,I表示微元中心位置。设i=1等价于I=1,i=n等价于I=n。
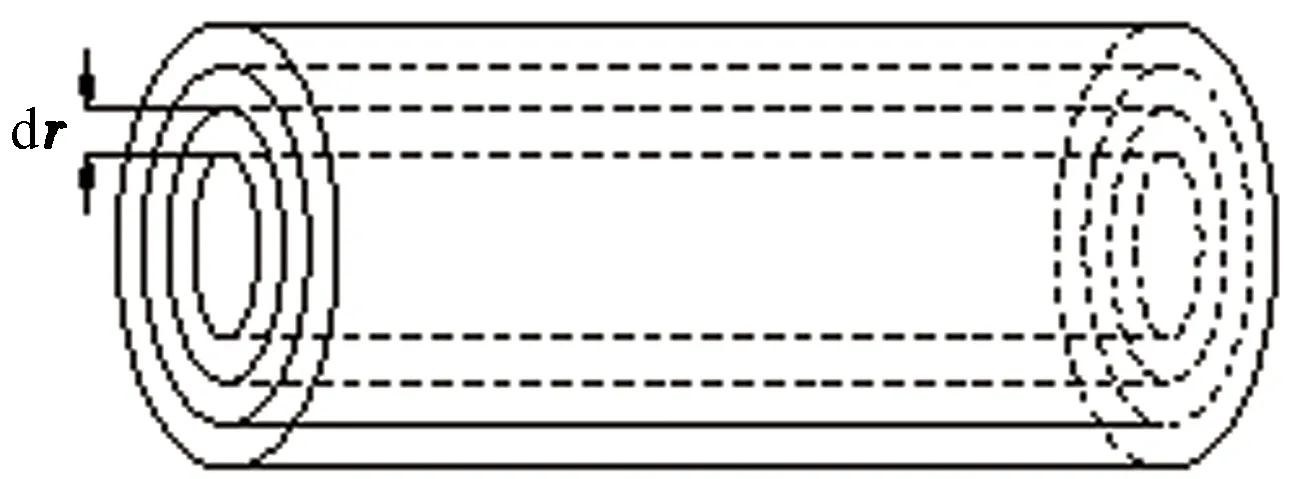
图1 圆管Poiseuille流动示意图Fig.1 Schematic of Poiseuille flow in circular pipe
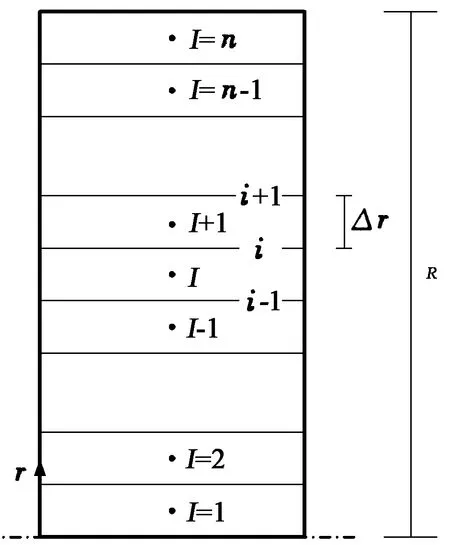
图2 圆管Poiseuille流动系统空间微元划分示意图Fig.2 Spatial grid distribution of Poiseuille flow in circular pipe
2.1 动量守恒方程
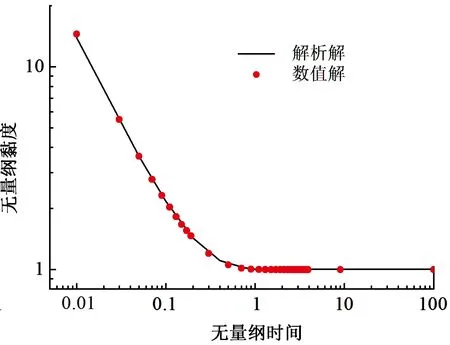
对于径向第I(1 (7) 式中,上标t+Δt表示下一时刻,s;t表示当前时刻,s;ρ为流体密度,kg·m-3;Δr为微元宽度,m;Δt为时间步长,s。 对于牛顿流体,其流变特性遵从牛顿内摩擦定律,即认为当流体受到外力作用时,其剪切速率与剪切应力的响应成正比。用流变方程描述为 (8) (1)I=0。界面处剪切速率可近似描述为 (9) (2)0 (10) (3)I=n。界面处剪切速率可描述为 (11) (1)恒平均速度边界。 (12) 式中,v0为施加的恒定平均速度,m·s-1。 (2)从0线性增加的平均速度边界。 (13) 式中,a为加速度,m·s-2。 (3)恒压力边界。 恒压力边界条件下圆管进出口压力均为恒定值,分别表示为 p(x=0)=p0, (14) p(x=L)=0 . (15) 式中,x为圆管轴向坐标,m;p(x=0)表示圆管入口位置处的压力,Pa;p(x=L)为管道出口压力,Pa;p0为施加的恒定压力,Pa。 初始时刻,流体静止,则有 (16) 剪切速率初始值为 (17) 剪切应力初始值为 τt=0i=0, 1≤i≤n. (18) 采用数值计算方法,通过编译程序对牛顿流体非稳态Poiseuille流动特性进行研究,采用控制单一变量法研究不同因素对于非稳态过程的影响规律。在数值计算过程中所需基础参数的默认值设置:μ=1 Pa·s,L=1 m,R=0.025 m,ρ=800 g·m-3,Δt=10-7s,n=20。研究某一参数影响时,仅改变该参数数值,其他参数保持默认值不变,对比计算结果,分析该参数对于非稳态过程的影响规律。 文献[4]中给出了恒压力边界条件下的牛顿流体非稳态Poiseuille流动速度分布函数的解析解。Erdogan[7]根据速度分布函数解析解,推导出流量随无量纲时间变化的解析解,表示为 (19) 式中,Q为非稳态过程测量流量;-π(ΔP/Δr)R4/8μ为流动达到稳定后的流量;λn为贝塞尔函数。 圆管流动中,在恒压力边界条件下,黏度与流量成反比[16]。即无量纲黏度应与无量纲流量互为倒数,则有 (20) 通过编译程序,对牛顿流体进行数值求解,与解析解进行对比,验证数值计算模型的可靠性。无量纲黏度随无量纲时间的变化如图3所示。 图3 恒压力边界条件下无量纲黏度数值解与解析解对比Fig.3 Comparison between numerical and analytical solutions of dimensionless viscosity under constant pressure condition 由图3可知,由数值模型计算求解的无量纲黏度变化规律与文献[7]一致,说明所建立的模型具有一定的可靠性。 根据上述牛顿流体非稳态Poiseuille流动的数值模型,编译程序,计算不同边界条件下的非稳态流动过程相关参数。 在Poiseuille流动的初始非稳态阶段,牛顿流体的速度分布随时间发生变化。以恒平均速度边界条件为例,取平均速度v0为0.05 m·s-1,其他参数根据默认值进行数值计算,记录不同时刻牛顿流体在圆管内的速度分布,如图4所示。 从图4可以看出,在流动发展的初始阶段,同一截面各位置处的流速相差较小,随着时间增加流速逐渐发展至稳定状态,管中心处流速最大,管壁处流速最小,整个截面中流速呈抛物线型分布,且不再随时间变化,仅与截面上所处位置有关,即流动得到充分发展。 由分析可知,Poiseuille流动的初始非稳态阶段主要是由径向速度分布发展的非稳态过程导致。 图4 恒平均速度边界下管内速度分布随时间变化Fig.4 Velocity distribution under constant average velocity conditions 4.1.1 不同流体黏度下非稳态流动差异 图5 不同黏度条件下无量纲黏度对比Fig.5 Dimensionless viscosity under different viscosity conditions 从图5可以看出,随着时间增加无量纲黏度逐渐降至1,即测试黏度逐渐接近真实黏度。根据无量纲黏度曲线的变化规律可知,同一时刻的真实黏度越大,其对应的无量纲黏度越小,即测量偏差越小,无量纲黏度趋近1所需的时间也越短,即流动达到稳定所需的时间也越短。 4.1.2 不同管径下的非稳态流动差异 图6 不同管径条件下无量纲黏度对比Fig.6 Dimensionless viscosity under different pipe diameter conditions 从图6可以看出,随着时间增加无量纲黏度逐渐降至1,即测试黏度逐渐接近真实黏度。同一时刻对应的管径越大,其对应的无量纲黏度越大,即测量偏差越大,无量纲黏度趋近1所需的时间也越长,达到稳定流动所需的时间也越长。 4.1.3 非稳态阶段无量纲化描述 图7为不同黏度和管径条件下无量纲黏度随无量纲时间变化。由图7可知,不同黏度和管径条件下,牛顿流体在非稳态过程中的无量纲黏度随无量纲时间的变化规律完全一致,即无量纲黏度可视为仅与无量纲时间相关的函数。 图7 不同黏度和管径条件下无量纲黏度随无量纲时间变化Fig.7 Change of dimensionless viscosity with dimensionless time under different viscosity and pipe diameter conditions 4.2.1 边界条件参数取值的影响 分别在各边界条件下取不同数值进行计算。具体取值情况为:①恒平均速度边界条件下,取平均速度分别为0.01、0.05、0.10 m·s-1;②从0线性增加的平均速度边界条件下,取加速度分别为0.01、0.1、1 m·s-2;③恒压力边界条件下,取边界压力分别为600、1 000、2 000 Pa。 4.2.2 边界条件类型影响 3种边界条件下的无量纲黏度对比如图9所示。 图8 各边界下不同参数下的无量纲黏度对比Fig.8 Comparison of dimensionless viscosities under different parameter in each boundary condition (21 ) 图9 不同类型边界条件下无量纲黏度对比Fig.9 Comparison of dimensionless viscosity under different kinds of boundary conditions 相比恒压力边界,恒平均速度边界条件下Poiseuille流动达到稳定所需的时间更短。而相比恒平均速度边界,非定常的平均速度边界会造成Poiseuille流动的非稳态过程显著延长。 (1)3种边界条件下非稳态过程使得黏度测量结果较流体真实黏度偏大。随着非稳态阶段时间增大测量黏度逐渐趋近于真实黏度。 (2)以无量纲黏度表征非稳态阶段特征,随着时间延长无量纲黏度逐渐降至1,且不同边界条件下达到1所对应的无量纲时间为定值。 (3)在同一类型边界条件下无量纲黏度仅与无量纲时间有关,与边界条件中的平均速度、压力及加速度均无关。 (4)对比不同类型边界条件,从0线性增加的平均速度边界会造成Poiseuille流动的非稳态过程显著延长,恒压力边界条件所需的流动发展时间次之,恒平均速度边界条件对应的非稳态过程最短。 : [1] 张国忠,高探贵.东黄复线停输再启动过程研究[J].油气储运,1996,15(9):37-40. ZHANG Guozhong, GAO Tangui. A study on the shutdown and restart course of Dong-Huang looping line[J]. Oil & Gas Storage and Transportation, 1996,15(9): 37-40. [2] 张树文,安家荣,张国忠.彩石输油管道停输再启动过程试验研究[J].油气储运,2000,19(10):45-48. ZHANG Shuwen, AN Jiarong, ZHANG Guozhong. Experiment and research on the shut-down and restart in Cainan-Shixi oil pipeline[J]. Oil & Gas Storage and Transportation, 2000,19(10):45-48. [3] 刘刚.胶凝原油管流特性研究[D].东营:石油大学(华东),2004. LIU Gang. An investigation of the characteristics of the gelled crude oil in pipeline[D]. Dongying:the University of Petroleum, China(East China),2004. [4] PAPANASTASIOU T, GEORGIOU G, ALEXANDROU A N. Viscous fluid flow[M]. Boca Raton: CRC Press, 1999. [6] ERDOGAN M E. On the unsteady unidirectional flows generated by impulsive motion of a boundary or sudden application of a pressure gradient[J]. International Journal of Non-linear Mechanics, 2002,37(6):1091-1106. [7] ERDOGAN M E. On the flows produced by sudden application of a constant pressure gradient or by impulsive motion of a boundary[J]. International Journal of Non-linear Mechanics, 2003,38(5):781-797. [8] ERDOGAN M E, IMRAK C E. On some unsteady flows of a non-Newtonian fluid[J]. Applied Mathematical Modeling, 2007,31(2):170-180. [9] SIDDIQUE I, SAJID Z. Exact solutions for the unsteady axial flow of non-Newtonian fluids through a circular cylinder[J]. Communications in Nonlinear Science and Numerical Simulation, 2011,16(1):226-238. [10] FETECAU C. Analytical solutions for non-Newtonian fluid flows in pipe-like domains[J]. International Journal of Non-Linear Mechanics, 2004, 39(2):225-231. [11] MUZYCHKA Y S, YOVANOVICH M M. Unsteady viscous flows and Stokess first problem[J]. International Journal of Thermal Sciences, 2010,49(5):820-828. [12] HAYAT T, ASGHAR S, SIDDIQUI A M. Some unsteady unidirectional flows of a non-Newtonian fluid[J]. International Journal of Engineering Science, 2000,38(3):337-345. [13] HAYAT T, KHAN M, SIDDIQUI A M, et al. Transient flows of a second grade fluid[J]. International Journal of Non-Linear Mechanics, 2004,39(10):1621-1633. [14] VINAY G, WACHS A, AGASSANT J F. Numerical simulation of weakly compressible Bingham flows: the restart of pipeline flows of waxy crude oils[J]. Journal of Non-newtonian Fluid Mechanics, 2006,136(2):93-105. [16] 李传宪.原油流变学[M].东营:中国石油大学出版社,2007. [17] CHEN Lei, LIU Gang, ZHANG Guozhong, et al. Transient stage comparison of Couette flow under step shear stress and step velocity boundary conditions[J]. International Communications in Heat and Mass Transfer, 2016,75:232-239. [18] 徐睿妤,刘刚,陈雷,等.同轴圆筒流变仪初始瞬态黏度的解析与数值研究[J].化工学报,2016,5:1784-1790. XU Ruiyu, LIU Gang, CHEN Lei, et al. Analytical and numerical studies on apparent viscosity in coaxial cylinder rotational rheometer during initial unsteady stage[J]. CIESC Journal, 2016,5:1784-1790. [19] 陈中良.恒流量启动胶凝原油管道初始结构破坏特性研究[D].青岛:中国石油大学(华东),2013. CHEN Zhongliang. Study on initial structural destruction properties of gelled crude oil pipeline under constant start-up flow condition[D]. Qingdao: China University of Petroleum(East China), 2013. [20] 左栋.胶凝原油恒压力启动特性研究[D].青岛:中国石油大学(华东),2009. ZUO Dong. An investigation of the characteristics of the gelled crude oil on constant pressure startup[D]. Qingdao: China University of Petroleum(East China), 2009. [21] 兰浩.胶凝原油屈服特性及环道启动过程研究[D].青岛:中国石油大学(华东),2010. LAN Hao. Study on the yield behavior and pipeline restart process of gelled crude oil[D]. Qingdao: China University of Petroleum(East China), 2010. [22] 蔡少敏.胶凝原油启动波传播及压缩特性研究[D].青岛:中国石油大学(华东),2015. CAI Shaomin. Simulation research on start-up wave propagation and compression characteristic of gelled crude oil[D].Qingdao: China University of Petroleum(East China),2015.2.2 剪切应力

2.3 剪切速率
2.4 边界条件
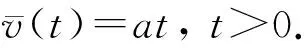
2.5 初始条件
3 牛顿流体非稳态Poiseuille流动
3.1 数值计算基础参数定义
3.2 数值计算模型验证
3.3 牛顿流体非稳态Poiseuille流动特点
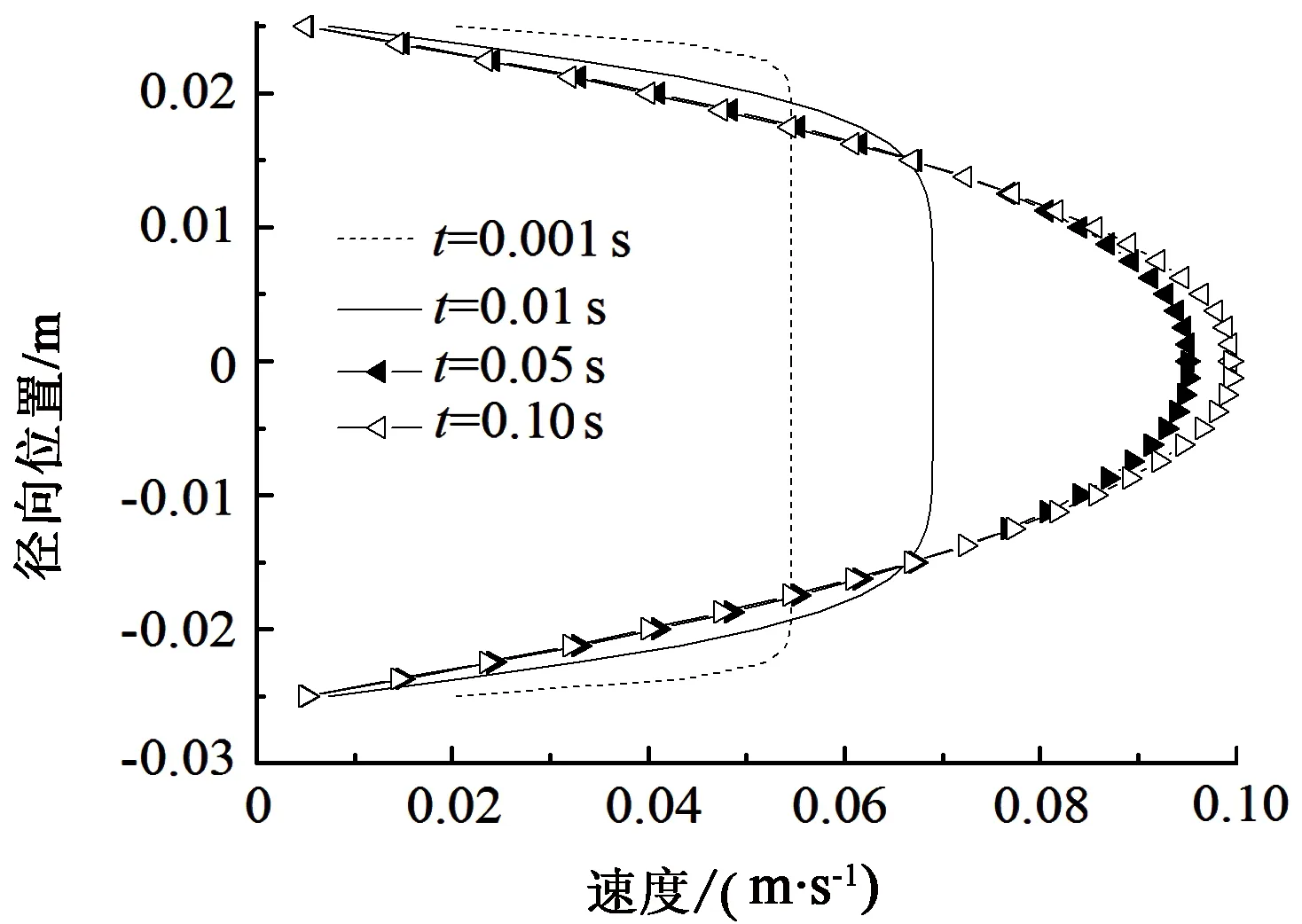
4 各因素对非稳态过程的影响规律
4.1 流体性质与管径参数影响
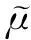

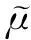

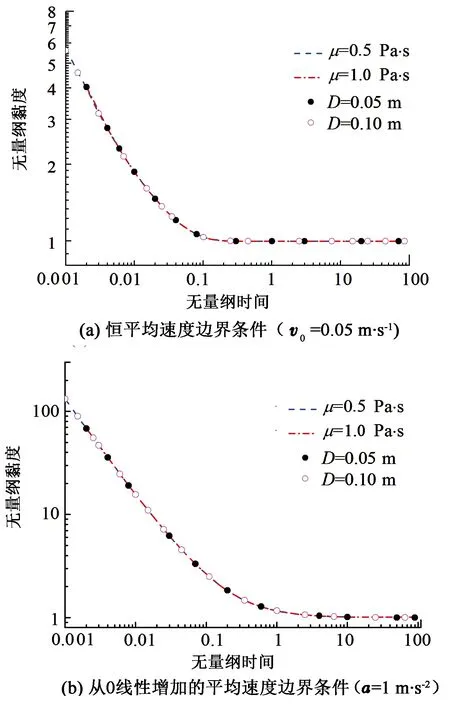
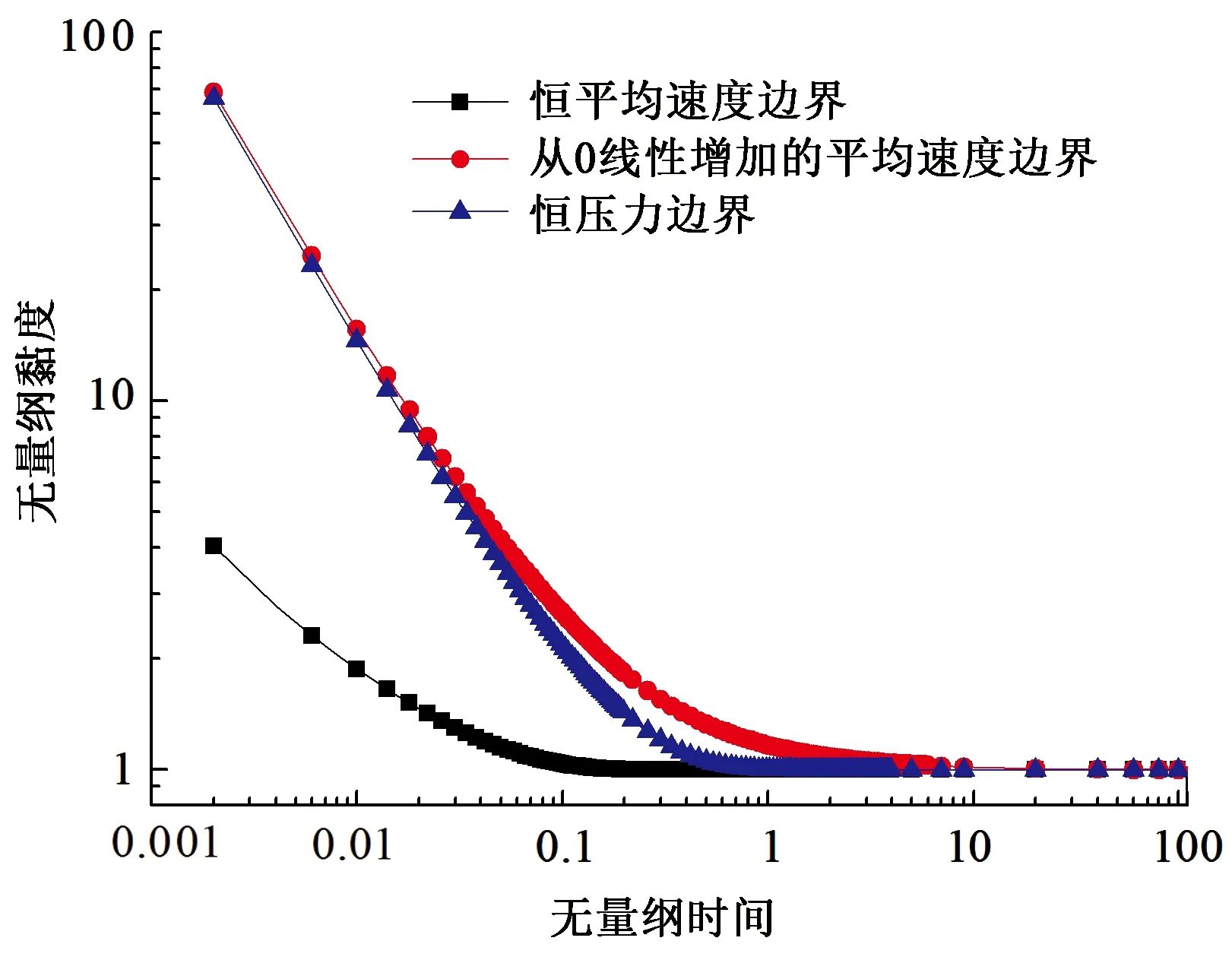
4.2 不同边界条件下非稳态Poiseuille流动


5 结 论
