基于Gaussian分布的三维非匹配性裂缝渗流规律

曲冠政, 彭 娇, 赵 凯, 高 伟, RANDY Hazlett,周德胜 ,曲占庆, 姜海龙

(1.西安石油大学石油工程学院,陕西西安 710065; 2.中国石油长庆油田分公司油气工艺研究院,陕西西安 610065;3.University of Tulsa,Tulsa USA 74104; 4.中国石油大学(华东)石油工程学院,山东青岛 266580)

在描述裂缝结构时通常将其等效为平板模型,但实际裂缝渗透率与平板模型结果偏差较大。目前关于裂缝描述及其渗流规律的研究还处于探索阶段[1-4];同时,现场裂缝具有大尺度匹配、小尺度非匹配的特点[5-6]。基于此,以页岩为例,统计并描述其高度分布特点,建立裂缝结构模型,生成满足研究条件的非匹配裂缝结构,采用Lattice Boltzmann方法,结合正交试验和灰色关联分析系统地研究流体在三维非匹配性裂缝中的渗流规律。

1 裂缝模型构造方法

1.1 Werierstrass-Mandelbrot函数法

Werierstrass-Mandelbrot函数(W-M函数)在描述二维自相似结构中具有广泛应用[7-9]。基于裂缝剖面线具有多尺度、自仿射的特征,引入W-M函数描述二维裂缝剖面结构,基本形式为

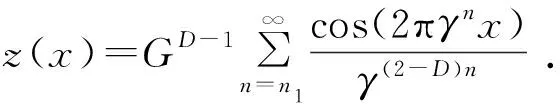
(1)

式中,z(x)为x位置处的高度,mm;G为尺度系数;D为自仿射分形维数;γ为与裂缝面轮廓频谱密度有关的量，一般取1.5;n1为描述W-M函数下限截止频率,其值可由γn1=1/Ls给出;Ls为测量样本长度,mm。

粗糙度计算方法为

(2)

式中,σ为粗糙度,mm;nl为下限截止频率，与样本长度有关，nl=1/L,mm-1;nh为上限截止频率,由测量仪器精度Lr决定,mm-1。

确定分形维数后,利用粗糙度计算公式求出尺度系数,结合W-M函数即可获得具有任意粗糙度和分形维数的二维粗糙曲线,将剖面线纵向延伸获取裂缝结构[7-9]。

1.2 基于Gaussian分布的裂缝构造方法

采用巴西劈裂试验将取自Barnett页岩的岩心Cabana-ZG-1、DARADO-ZG-1、punta-piedra-ZG-1 和Dorado-Sur12劈裂成人工裂缝,扫描裂缝面数据并重构,如图1所示。裂缝面高度Gaussian分布拟合如图2所示。

图1 页岩裂缝面重构图Fig.1 Rough fracture surface reconstitution

图2中蓝色部分为裂缝面高度分布直方图,红色曲线为依据裂缝面高度分布数据计算出的Gaussian正态分布曲线。4块页岩裂缝面高度分布特征与计算出的Gaussian分布曲线间有出入,但总体上符合Gaussian分布规律。考虑到岩心尺寸和测量手段等对结果的干扰,结合裂缝面高度分布的实际情况,可认为其分布符合Gaussian分布规律。

根据页岩裂缝面高度分布特点,采用Gaussian分布函数构造裂缝结构。裂缝结构中,特征描述参数分为裂缝开度和裂缝面粗糙性描述参数。生成裂缝面结构后,裂缝开度可任意设定。因此关键问题是裂缝面的构造。构建裂缝面时,需要考虑的主要因素为裂缝面高度概率分布及其在三维空间的展布规律[10-11]。分别采用Gaussian分布函数和自相关函数描述裂缝面高度概率分布和高度在三维空间的展布规律。裂缝结构示意图如图3所示。

图3中裂缝结构由上下两个裂缝面组成,裂缝面在局部可能会接触。两裂缝面可分别视为在平均高度平面h0+和h0-波动,两个平面与xy平面平行。面Sp+和Sp-可表示为

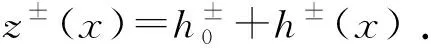
(3)

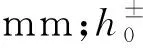
裂缝开度定义为

b(x)=z+(x)-z-(x) .

(4)

式中,b(x)为裂缝开度,mm;z+(x)为上裂缝面x处高度,mm;z-(x)为下裂缝面x处高度,mm。

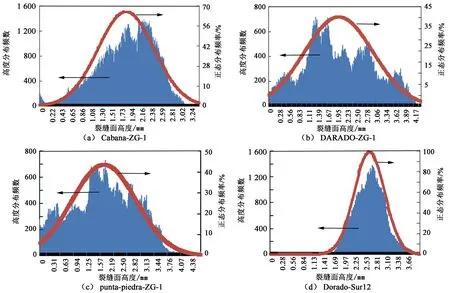
图2 裂缝面高度Gaussian分布拟合图Fig.2 Fitted Gaussian distribution of fractures surface height

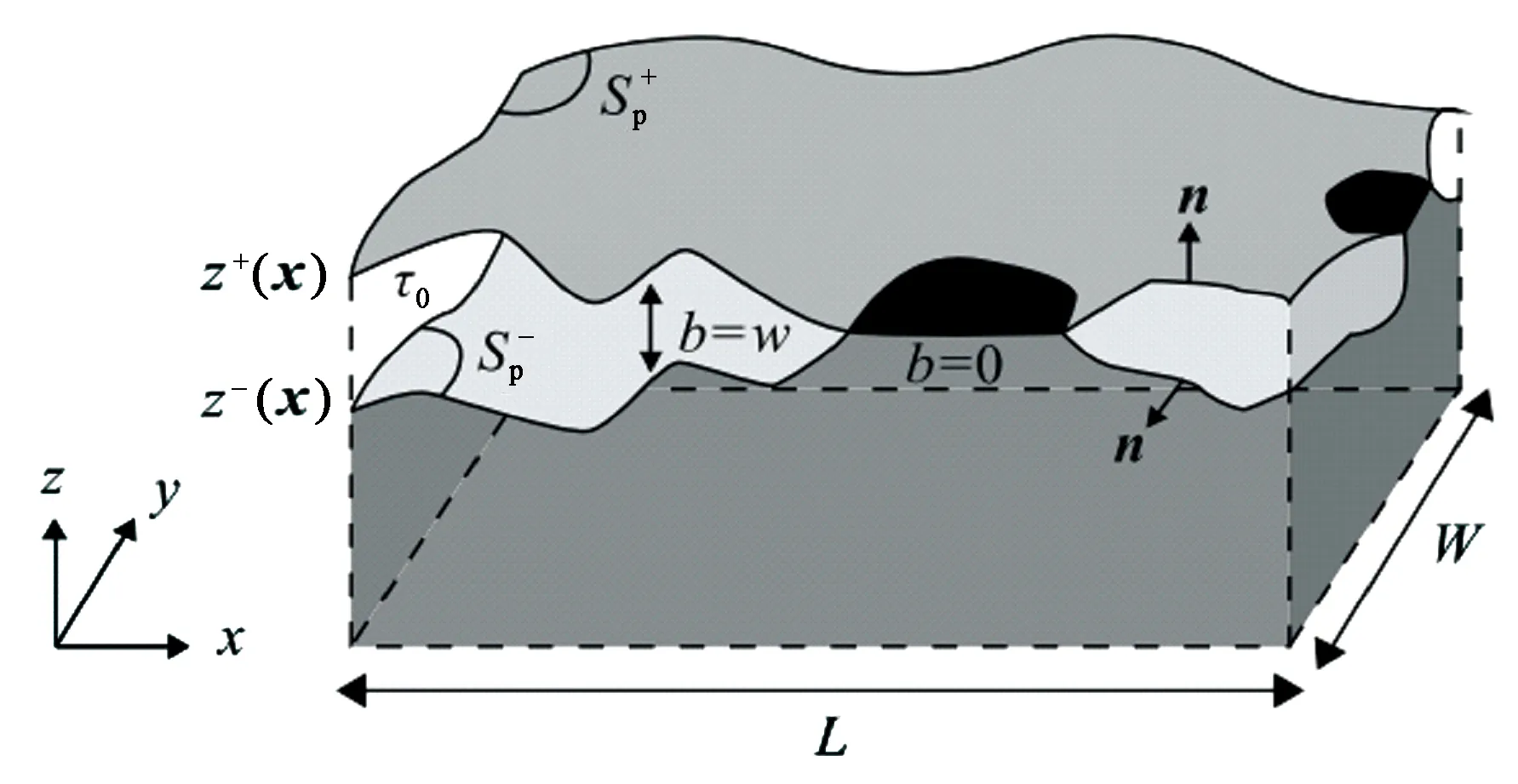
图3 裂缝结构示意图Fig.3 Sketch map of fracture structure

裂缝面的波动随其所在位置不同而差异很大。由于波动是基于平均面,因此裂缝面波动平均值为0,即

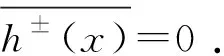
(5)

裂缝面间平均距离定义为

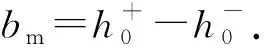
(6)

式中,bm为裂缝面间平均距离,mm。

采用Gaussian分布函数描述其高度分布概率,表达式为

(7)

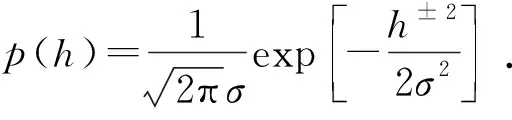
(8)

式中,P(H)和p(h)分别为概率函数和概率密度函数;h为裂缝高度,mm。

自相关函数是描述信号间关联程度的函数。对于三维裂缝面,可表示为

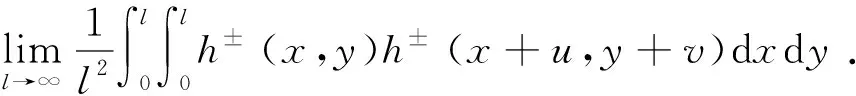
(9)

式中,Ch+(x,y)和Ch-(x,y)为自相关函数,两者相等,mm;h+(x,y)和h-(x,y)为裂缝面高度分布,mm;u和v为滞后,mm;l为周期,mm。

相比于常规数域中求解问题的局限性,在傅里叶域求解函数具有明显优势;自相关函数在傅里叶域中对应于功率谱密度函数,将信号采用不同时间域或空间域正弦信号的组合。正弦信号具有不同的波长、振幅和相位,振幅的平方为功率,振幅与波数的关系曲线为功率谱,功率谱的正交化即为功率谱密度。功率密度函数谱矩能有效描述裂缝面粗糙度。功率密度函数谱矩[12]定义为

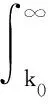
(10)

其中

k0=2π/λ0.

式中,mn为n阶矩;k0为对应于剖面线长度λ0的波数;S(k)为功率谱密度函数,即自相关函数的Fourier变换。

确定Gaussian概率分布函数和自相关函数(功率谱密度函数)后即可建立裂缝结构的基本模型。功率谱密度函数与波数间关系[12]表达式为

S(k)=Ck2D-7.

(11)

考虑粗糙度沿裂缝面两方向上的分布规律,引入各向异性系数b/a度量其非均质性。当b/a<1时,非均质性垂直于x方向;当b/a=1时,粗糙度为均质分布;当b/a>1时,非均质性平行于x方向。具体表达式为

S(k)=C[(kx/a)2+(ky/b)2]D-3.5.

(12)

采用Gaussian概率分布函数和自相关函数分别描述粗糙度分布概率、裂缝面粗糙度间的关联性,并引入分形维数、非均质性系数描述粗糙度在裂缝面的展布情况。以上函数及相关参数已足以描述拉张型粗糙裂缝结构,但研究表明:实际的粗糙裂缝两面结构间存在一定的非匹配性,傅里叶域中,长波长情况下两裂缝面是匹配的;而当波长小于某一阀值时,裂缝结构表现为非匹配性。Brown[5]首次提出非匹配长度的概念,Glover等[6]在Brown研究的基础上发展了非匹配性表征方面的理论:在傅里叶域中,引入临界波长λc衡量其匹配情况。当λ<λc/2时,采用两个独立的随机数据源(R1、R2)生成裂缝面,在此波长范围内两裂缝面完全非匹配;当λ>λc/2时,引入R1和R2的线性组合R3形成随机数据源,表达式为

(13)

式中,R1、R2和R3为随机数据源;λ为波长;β为匹配因子,代表最长波长时最大程度的匹配度;kc为非匹配波长对应的波数。

明确各参数后,以R1为生成上裂缝面的随机数据源,R3为生成下裂缝面的随机数据源。生成的两裂缝面结构分形维数、粗糙度、各向异性分布均一致,只有非匹配长度存在差异。根据以上理论,依照研究需要可任意设置裂缝面分形维数、粗糙度、各向异性系数及非匹配长度等参数。

考虑到计算资源问题,生成裂缝结构的表观尺寸限定为3 mm×3 mm。根据研究需要共生成20组不同的裂缝面结构,部分粗糙裂缝面结构如图4所示。

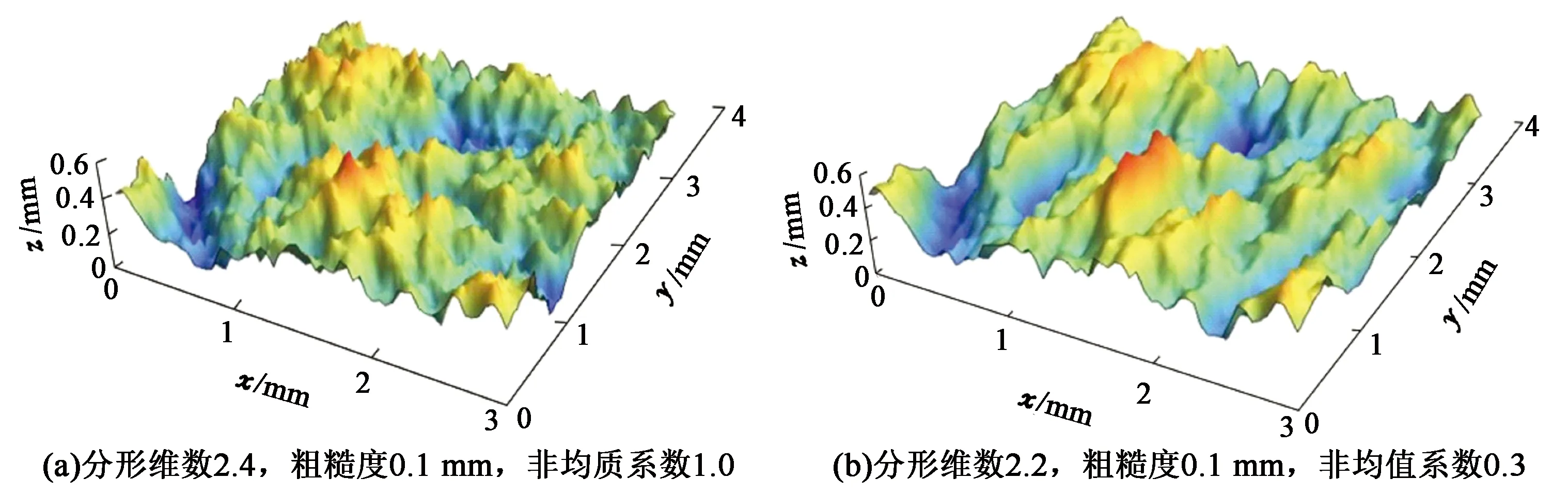
图4 粗糙裂缝面Fig.4 Rough surface morphology

图5为生成的部分裂缝结构及其开度分布,裂缝面分形维数均为2.2,粗糙度0.1 mm;其中图5(a)、(b)各向异性系数为1,图5(c)、(d)各向异性系数为3。各裂缝结构由于设定的裂缝结构参数的差异性,导致所生成的裂缝平均开度各异。

为直观展现不同裂缝面间的差异,选取裂缝结构某一剖面线分布定性考察其分布特点,鞠杨等[2]和张程宾等[3]采用Weierstrass-Mandelbrot函数生成与图6类似的满足粗糙度和分形维数的粗糙剖面线并将其横向延伸,沿纵向影像得到匹配性裂缝结构;郑宏等[4]则采取分形插值法生成满足设定分形维数的粗糙裂缝结构,并截取某一剖面线并影像进行粗糙裂缝渗流的研究,其在研究中也没有考虑非匹配性的影响。

图6为沿x=2 mm处截面y方向上各裂缝结构剖面线分布。当非匹配长度为0.3 mm时,沿y方向上裂缝上下面吻合很好,极个别点处裂缝开度略有偏移;当非匹配长度为0.7 mm、可明显见到部分区域裂缝面的非一致性,但从整体尺度上看两裂缝结构面基本保持一致,该情况下的裂缝开度相比较与非匹配长度0.3 mm情况下明显增加,裂缝开度的波动幅度较之非匹配长度0.3 mm情况增加;当非匹配长度为0.7 mm、裂缝面各向异性系数为3时,相比于各向异性系数为1情况下,裂缝平均开度略有增加,同时裂缝开度波动幅度明显增加;而当非匹配长度为2.1 mm时,裂缝面间差异明显,裂缝间距较之非匹配长度较小的情况明显增加,波动幅度亦明显增加。>

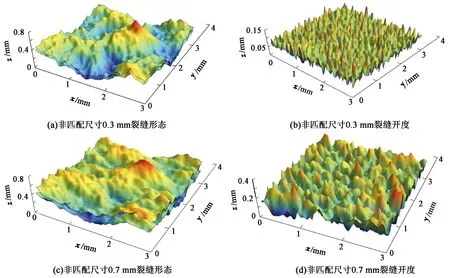
图5 构造的裂缝结构Fig.5 Constructed fracture structures

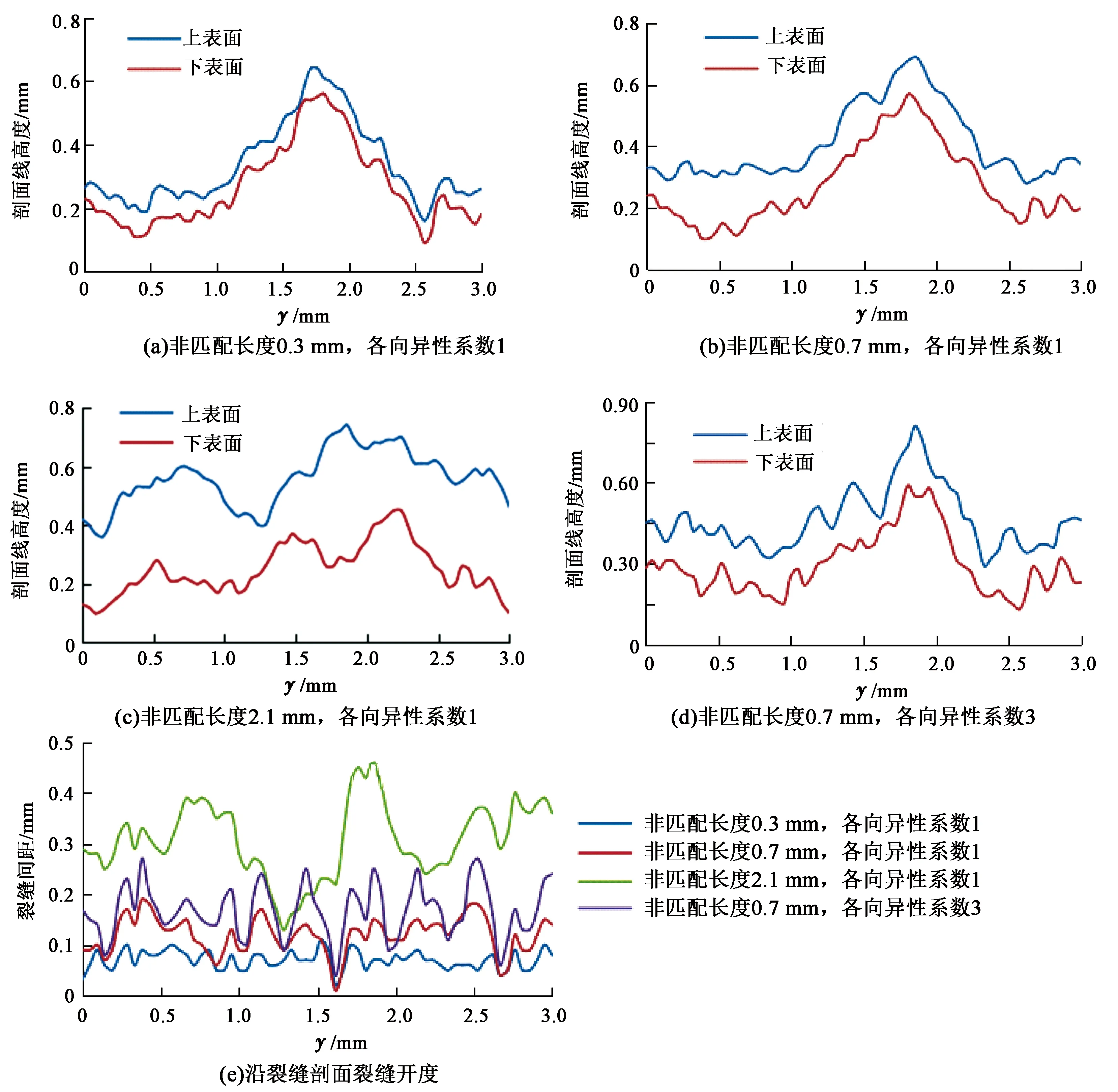
图6 x=2 mm处裂缝结构剖面线Fig.6 Fracture profiles along x=2 mm

2 渗流模拟方法

研究流体渗流问题的方法归纳起来包括物理实验法、理论研究方法及数值模拟方法。在处理微尺度问题上,物理实验方法受实验成本、仪器精度、测量手段及实验条件等影响很大;理论研究方法通常采取各种简化条件,研究条件与流体渗流条件有较大出入;数值模拟方法可根据研究需要设置物理模型,并结合相应渗流理论对研究目标重点分析,能够克服物理实验方法的缺陷,因此在研究目标较为复杂且对实验要求较高时,数值模拟方法是较好的选择。考虑到研究目标的特征尺度及裂缝面的复杂性,采用Lattice Boltzmann方法模拟流体在裂缝中的渗流[13]。

2.1 Lattice Boltzmann模型

Lattice Boltzmann方法基于分子热运动和统计理论,将无规则的分子热运动简化为格子规则化的碰撞和迁移运动。Lattice Boltzmann方法中最关键的因素是格子运动规律和平衡态分布函数。在单相流模拟方面,LBM-BGK模型被广泛接受;三维流体运移模拟中,以Qian等[14]提出的D3Q19模型应用最为广泛。该模型演化方程、平衡态分布函数及粒子权重系数表达式分别为

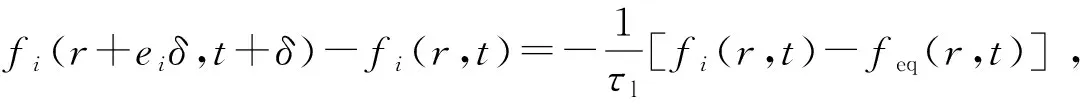
(14)

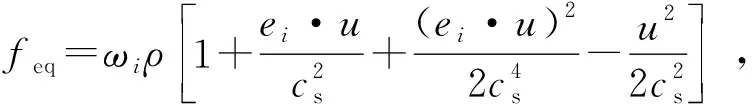
(15)

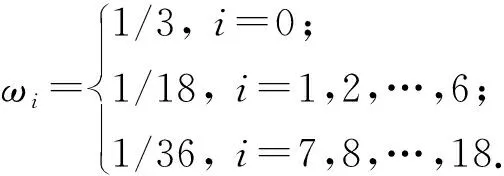
(16)

式中,cs为格子声速,模型中为(1/3)0.5;ei为i方向格子速度,i=0,1,…,18;feq为D3Q19模型平衡态分布函数;fi为粒子密度分布函数;r为粒子空间位置;ωi为i方向上的粒子权重系数;τl为松弛时间;δ为时间步长。

流体宏观密度和速度分别为

(17)

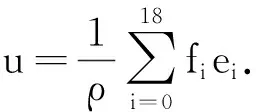
(18)

边界条件设置上,根据在裂缝中流体渗流的实际情况,将纵向上边界设为光滑边界条件;考虑到裂缝面的粗糙性,在裂缝面上采用标准反弹边界。

根据量纲等效原则,裂缝渗透率和格子渗透率关系式为

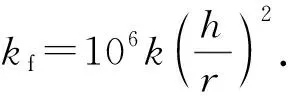
(19)

式中,kf为裂缝渗透率,μm2;k为格子渗透率;r为格子分辨率。

采用Lattice Boltzmann方法专业软件PowerFLOW进行相关模拟计算。陈耀松等[15]、Wang等[16]、Du等[17]的研究成果证明了软件的准确性和可靠性。采用平板模型和圆管模型验证计算方法的可靠性,理论值与模拟值吻合很好。

2.2 计算网格划分

空间网格采用笛卡尔正交网格,PowerFLOW软件中是以分辨率的形式表示网格结构。经计算当格子分辨率大于10以后,模拟结果基本保持不变。因此选取格子分辨率为10。

2.3 流体运移模拟

首先固定分形维数、粗糙度和各向异性系数,建立不同非匹配长度的裂缝结构模型,进行流体渗流模拟;然后,从所建立的非匹配性裂缝模型中,以一定间隔选取其中4个裂缝结构,对比两面完全吻合和非匹配情况下的流体渗流特征;此外,综合考察分形维数、粗糙度和各向异性系数等裂缝特征参数对流体渗流的影响。

采用水作为模拟流体,温度20 ℃,密度0.998×103kg/m3,运动黏度1.006×10-6m2/s,采取入口速度,出口压力作为边界条件。入口速度设为1.0 m/s,出口压力采用标准大气压,即1.013 25×105Pa。为保证模拟结果的收敛,模拟时间设为20 000时间步长。为保证模拟中流动为达西渗流,模拟中恒定雷诺数为10。

3 模拟结果分析

3.1 非匹配长度影响

如表1所示,共进行20组非匹配长度影响的模拟,模拟中裂缝表观尺寸3 mm×3 mm,分形维数2.2,粗糙度0.1 mm,各向异性系数均为1。表1中的裂缝开度为控制两裂缝面不接触所需的最小平均开度。随非匹配长度增加,维持裂缝不接触所需的平均开度总体呈增加趋势。

表1 非匹配裂缝模拟数据

图7为裂缝渗透率与非匹配长度的关系曲线。由图7可得:裂缝渗透率随非匹配长度增加呈迅速增长并在后期趋于稳定的趋势。对比理想平板模型渗透率,在相同开度情况下裂缝渗透率的变化趋势基本与理想平板模型一致;粗糙性的影响导致裂缝渗透率偏离理想平板模型结果且偏差较大。

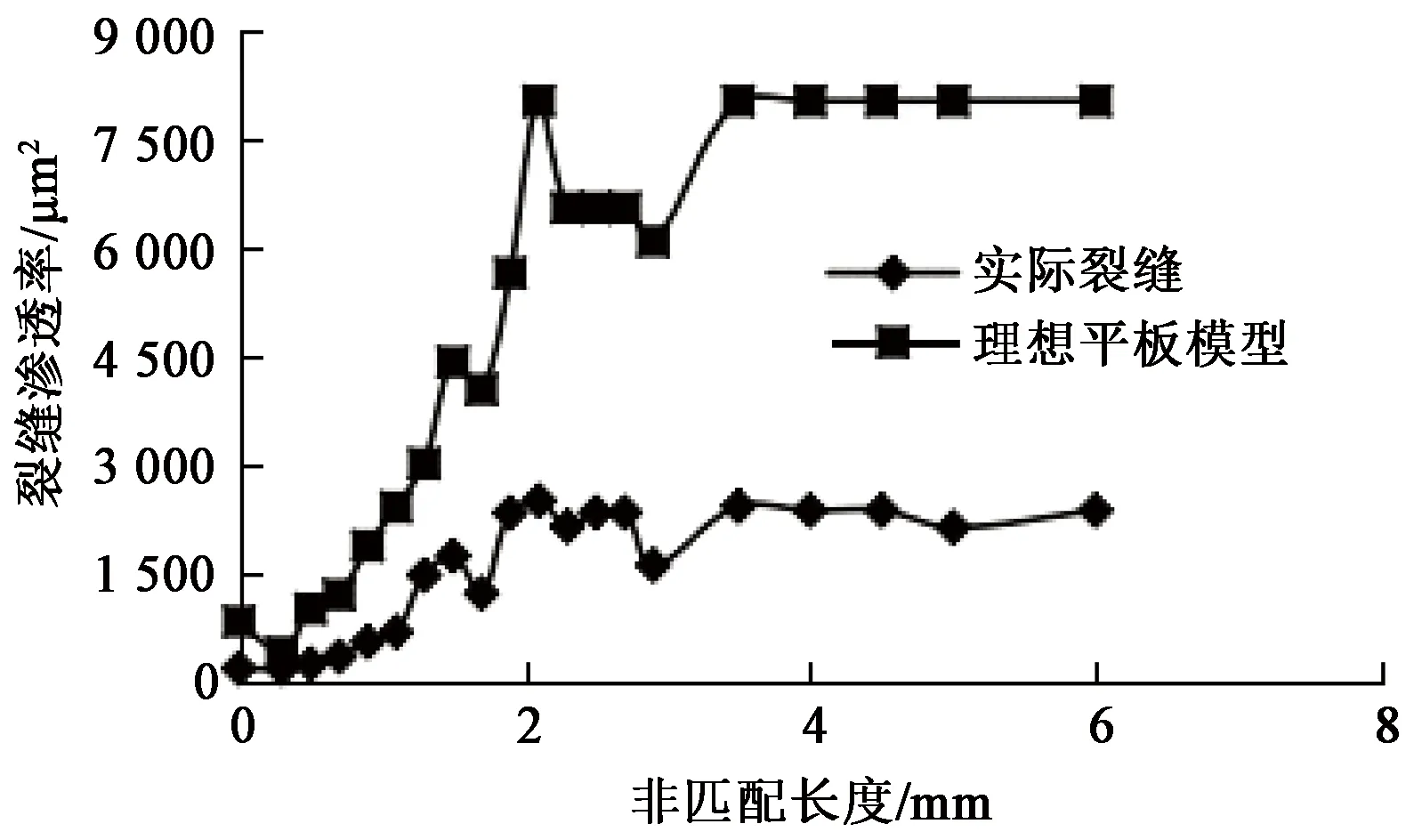
图7 裂缝渗透率与非匹配长度关系Fig.7 Relationship between fracture permeability and mismatch length

考虑粗糙性影响的裂缝渗透率计算公式[18-20]概括起来为

(20)

式中,τ为迂曲度;A和B为系数。

式(20)中采用粗糙度和迂曲度修正裂缝粗糙性的影响,但研究中并未考虑非匹配性的影响。参考裂缝面匹配的裂缝渗透率计算模型,修正非匹配性的影响公式为

(21)

式中,k′为非匹配性裂缝渗透率,μm2;α为裂缝面非匹配性综合修正系数。

非匹配性修正系数反映了非匹配性对裂缝渗透率的影响程度,该值越大则表明非匹配裂缝渗透率越大。非匹配长度与非匹配性综合修正系数关系如图8所示。受粗糙性影响,实际裂缝渗透率约为理想平板模型渗透率的20%～50%;以裂缝结构表观尺寸3 mm为界,当非匹配长度小于3 mm时,非匹配性综合修正系数随非匹配长度变化有较大幅度的波动,当非匹配长度大于3 mm后,非匹配性综合修正系数基本趋于稳定。

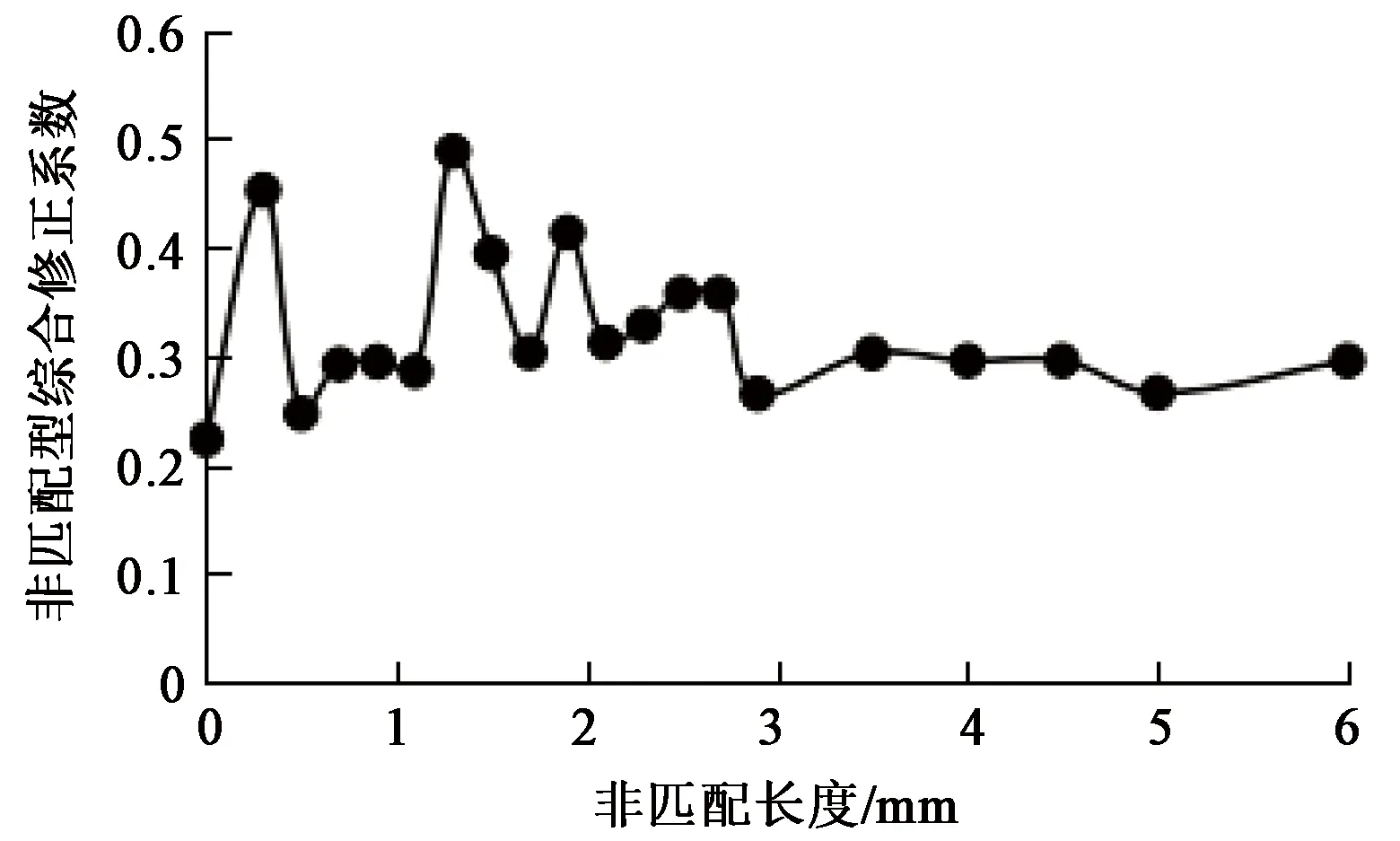
图8 非匹配长度与非匹配性综合修正系数关系Fig.8 Relationship between mismatch length and mismatch comprehensive coefficient

3.2 非匹配性裂缝与匹配性裂缝结构对比

固定分形维数2.2、粗糙度0.05 mm、各向异性系数1.0,考察非匹配长度0.3、1.1、1.9和2.7 mm情况下非匹配性裂缝结构及采用非匹配性裂缝结构两裂缝面分别组成匹配性裂缝结构等3种情况下的裂缝渗流能力,结果如图9所示。两种匹配性裂缝结构的渗流能力基本保持一致,而非匹配性裂缝的渗透率明显比匹配性裂缝渗透率低。

如图10所示,裂缝结构可视为由众多平板模型串联而成。流体在裂缝中的渗流阻力,一方面来自于众多平板模型基本单元体结构的渗流阻力,另一方面来自于相邻平板模型基本单元体结构间的衔接渗流阻力。衔接区域形态的突然改变更容易出现如图11 中裂缝面改变率较大区域形成的回流区,回流区的出现极大地增加了流体的渗流阻力。

对于非匹配性裂缝结构,同样将其等效为平板模型结构分析其渗流阻力:除具有平板模型基本单元体和基本单元体间的衔接渗流阻力外,还包括非匹配区域的渗流阻力;由于结构间的非匹配性,在非匹配区域裂缝结构形态变化率较大,造成非匹配性裂缝渗透率低于匹配性裂缝渗透率。

图9 裂缝结构渗透率对比Fig.9 Permeability comparison among different fracture structures

图10 裂缝等效平板模型 Fig.10 Equivalent parallel plate model of rough fracture

图11 裂缝渗流速度矢量Fig.11 Velocity vector in rough fracture

3.3 非匹配性裂缝渗透率影响因素敏感性分析

正交试验设计可定性确定各因素对考察目标的影响程度,最显著特点是以具有代表性的有限个方案反映大量方案中所包含的本质规律和矛盾主次[36]。非匹配性裂缝结构中,裂缝开度是影响渗透率的最主要因素,其他影响因素有非匹配长度、粗糙度、分形维数和各向异性系数。其中由于裂缝开度与非匹配长度存在正相关关系,裂缝开度的波动受迫于非匹配长度的变化。因此,进行正交试验设计时两个因素中只选取非匹配长度,即考虑非匹配长度、粗糙度、分形维数和各向异性系数,采用四因素三水平正交试验设计确定模拟方案如表2所示,表3为计算的裂缝渗透率及其基本参数数据。

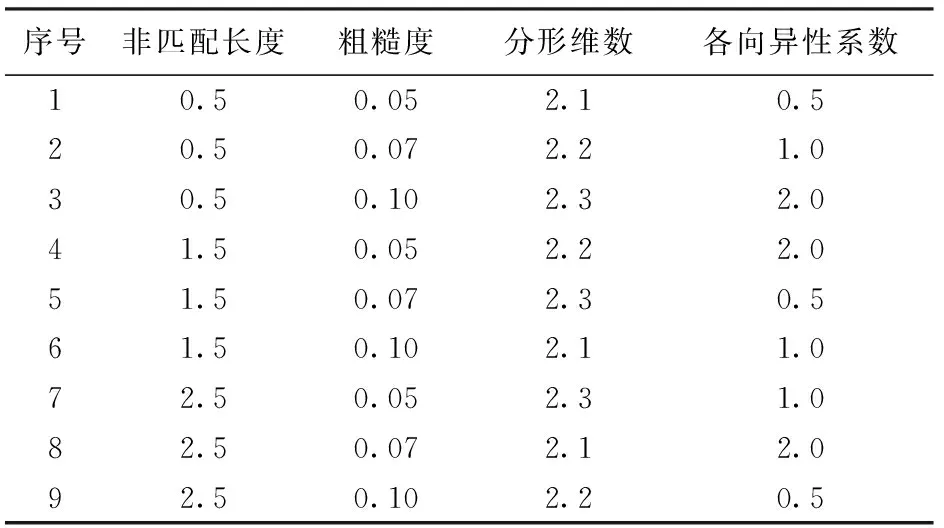
表2 正交试验设计因素

表3 Lattice Boltzmann方法模拟渗透率Table 3 Permeability value based on LatticeBoltzmann simulation

为全面分析各因素对裂缝渗透率的影响程度,在进行相关灰色关联分析计算时考虑裂缝开度的影响。灰色关联分析方法对样本容量和分布的规律性均没有要求,并且分析结果与定性分析结果相吻合,不会出现量化分析结果与定性分析结果不符的情况。因此以上试验设计方案和灰色关联分析所采用数据方案不会影响分析结果。具体步骤如下[21]。

将裂缝渗透率视为目标数列:X0={X0(s)|s=1,2,3,…,9},非匹配长度、粗糙度、分形维数、各向异性系数、裂缝开度视为因素数列Xi={Xi(s)|s=1,2,3,…,9},其中s为因素取值个数,i为因素数列个数。为消除量纲影响,将因素数列和目标数列进行均值化无量纲处理,经过均值化方法处理的各指标数据构成的协方差矩阵既可以反映原始数据中各指标变异程度上的差异,也包含各指标相互影响程度差异的信息。数据无量纲化处理后,计算因素数列Xi(s)与目标数列X0(s)的关联系数,表达式为

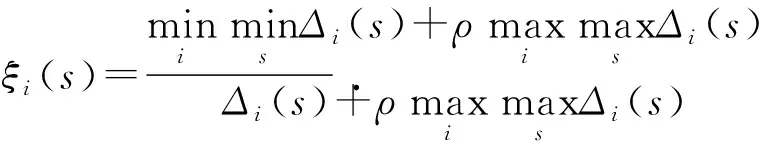
(22)

式中,ρ为分辨系数,取0.5;Δi(s)=|X0(s)-Xi(s)|为第某时刻目标数列与因素数列的绝对值差。

根据式(22)可求得因素数列Xi与目标数列X0的关联系数序列ξi={ξi(s)|s=1,2,3,…,9},利用平均值法可得各因素的关联度γi为

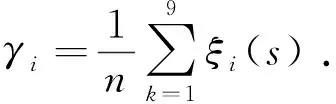
(23)

经计算,各因素的关联系数为0.58～0.82;裂缝开度的影响程度最大,其关联系数为0.813 3,是影响非匹配性裂缝渗透率的主要因素,但并不占绝对主导地位;其他依次为粗糙度0.743 7,分形维数0.671 4,各向异性系数0.660 4和非匹配长度0.586 8;非匹配长度、粗糙度、分形维数和各向异性系数对非匹配性裂缝渗透率的影响均不可忽略;粗糙度,即裂缝面高度分布偏离程度为影响非匹配性裂缝渗透率的次主要因素;分形维数,即粗糙度在裂缝面分布规律的影响位于第三位;最后为非匹配长度和各向异性系数,两者对非匹配性裂缝渗透率的影响程度相近。

在目前的压裂开发设计中,通常只考虑裂缝开度与储层油气渗流条件的匹配性。而灰色关联分析结果显示:裂缝面粗糙度及粗糙度在裂缝面的整体分布规律(分形维数)及横纵向分布规律(各向异性系数)、非匹配长度均对裂缝渗流具有不可忽略的影响。相比于两面完全吻合的裂缝结构,在裂缝平均开度相同情况下,匹配性裂缝的渗透率比非匹配性裂缝的略大;随粗糙度和分形维数增加,裂缝渗流阻力明显增加,渗透率降低。目前的压裂设计中,研究主要集中于所形成裂缝结构的缝长和缝宽等宏观尺度参数,而对于裂缝结构面参数对渗流能力的研究较少。因此在以后的研究中,建议加强储层岩石物性特征(泊松比、弹性模量等)及压裂泵注程序等对裂缝面粗糙性影响方面的研究。在保证裂缝开度的情况下,尽可能避免使裂缝结构产生非匹配性,同时降低裂缝面的粗糙度和分形维数。

3.4 各向异性系数的影响

固定分形维数2.2、粗糙度0.10 mm情况下,考察各向异性系数与粗糙裂缝渗透率的关系,结果如图12所示。随各向异性系数增加,渗透率呈先上升后下降趋势;在裂缝面粗糙度分布各向同性时,模拟裂缝渗透率值并不是最大;实例中,当各向异性系数为0.7时,模拟渗透率值最大,为402.45 μm2。

图12 各向异性系数与裂缝渗透率关系Fig.12 Relationship between anisotropy coefficient and permeability

4 结 论

(1)采用统计学公式Gaussian分布函数描述裂缝面结构分布特点,考虑分形维数、非匹配长度、粗糙度、各向异性等因素,建立更符合实际的真三维裂缝结构模型。实例中,裂缝渗透率仅为理想平板模型渗透率的20%～50%,裂缝面的粗糙性对流体渗流具有较大的阻力作用。

(2)采用上、下面结构影像得到的匹配性裂缝渗透率值基本保持一致,非匹配性裂缝渗透率比匹配性裂缝渗透率值略小。将裂缝结构视为平板模型结构的串联组合,分析匹配性裂缝和非匹配性裂缝渗流阻力的差别。非匹配性裂缝衔接区域形态的突然改变更容易出现回流区域,回流区域增加了流体的渗流阻力。

(3)裂缝开度和粗糙度是影响非匹配性裂缝渗透率的最主要因素;其他依次为分形维数、各向异性系数和非匹配长度。粗糙度分布规律同样对非匹配性裂缝渗透率具有重要作用。

(4)实例中,随各向异性系数增加,粗糙裂缝渗透率呈先上升后下降趋势,且当各向异性系数取0.7时,粗糙裂缝渗透率取最大值。

:

[1] 速宝玉,詹美礼,赵坚.仿天然岩石裂隙渗流的实验研究[J].岩土工程学报,1995,17(5):19-24.

SU Baoyu, ZHAN Meili, ZHAO Jian. Study of fracture seepage in the imitative nature rock [J].Chinese Journal of Geotechnical Engineering,1995,17(5):19-24.

[2] 鞠杨,张钦刚,杨永明,等.岩体粗糙单裂隙流体渗流机制的实验研究[J].中国科学(技术科学),2013,43(10):1144-1154.

JU Yang, ZHANG Qingang, YANG Yongming, et al. An experimental investigation on the mechanism of fluid flow through single fracture of rock[J].Science China (Technological Science),2013,43(10):1144-1154.

[3] 张程宾,陈永平,施明恒,等. 表面粗糙度的分形特征及其对微通道内层流流动的影响[J]. 物理学报,2009,58(10):7050-7056.

ZHANG Chengbin, CHEN Yongping, SHI Mingheng, et al. Fractal characteristics of surface roughness and its effect on laminar flow in microchannels[J]. Acta Physica Sinica, 2009,58(10):7050-7056.

[4] 樊火,郑宏.基于MRT-LBM的分形裂隙网络渗流数值模拟[J].中国科学(技术科学),2013,43(12):1338-1345.

FAN Huo, ZHENG Hong. MRT-LBM based numerical simulation of seepage flow through fractal fracture networks[J].Science China(Technological Science), 2013,43(12):1338-1345.

[5] BROWN S R. Simple mathematical model of a rough fracture[J]. Journal of Geophysical Research,1995,100(B4):5941-5952.

[6] GLOVER P W J, MATSUKI K, HAYASHI K, et.al. Synthetic rough fractures in rocks[J].Journal of Geophysical Research,1998,103(85):9609-9620.

[7] GANTI S, BHUSHAN B. Generalized fractal analysis and its applications to engineering surfaces[J].Wear,1995(180):17-34.

[8] MAJUMDAR A, TIEN C L. Fractal characterization and simulation of rough surfaces[J].Wear,1990(136):313-327.

[9] THOMA T R, ROSEN B G, AMINI N. Fractal characterization of the anisotropy of rough surfaces[J].Wear,1999(232):41-50.

[10] BROWN S R, SCHOLZ H. Closure of rock joints[J]. Journal of Geophysical Research,1986,9(B5):4939-4948.

[11] BROWN S R, SCHOLZ C H. Broad bandwidth study of the topography of natural rock surfaces[J].Journal of Geophysical Research,1985,90(12):575-582.

[12] POWER W L, TULLS T E. Euclidian and fractal models for the description of rock surface roughness[J].Journal of Geophysical Research,1991,96(B1):415-424.

[13] 张磊,姚军,孙海,等.利用格子Boltzmann方法计算页岩渗透率[J].中国石油大学学报(自然科学版),2014,38(1):87-91.

ZHANG Lei, YAO Jun, SUN Hai, et.al. Permeability calculation in shale using Lattice Boltzmann method[J]. Journal of China University of Petroleum(Edition of Natural Science),2014,38(1):87-91.

[14] QIAN Y H. Lattice BGK models for Navier-Stokes equation[J].Europhysics Letters,1992,17(6):479-484.

[15] 陈耀松,单肖文,陈沪东,等.计算流体力学的新方向及其在工业上的应用[J].中国科学(技术科学),2007,37(9):1107-1116.

CHEN Yaosong, SHAN Xiaowen,CHEN Hudong, et al. New direction of computational fluid dynamics and its application on industry[J].Science China(Technological Sciences), 2007,37(9):1107-1116.

[16] WANG Yiwei, WANG Yang, AN Yiran, et al. LBM calculation of high-speed train aerodynamics[J]. Science China(Technological Sciences), 2008,38(11):1795-1804.

[17] DU Tezhuan, LI Xiangqun, ZHANG Xialing, et al. Lattice Boltzmann method used for the aircraft characteristics computation at high angle of attack[J].Science China(Technological Sciences),2010,53(8):2068-2073.

[18] LOUIS C. A study of groundwater flow in jointed rock and its influence on stability of rock masses[D].London:Imperial College of Science and Technology,1969.

[19] LOUIS. Rock hydraulics in rock mechanics[M].New York:Springer-Verlag,1974.

[20] XIAO Weimin, XIA Caichu, WANG Wei, et al. Combined effect of tortuosity and surface roughness on estimation of flow rate through a single rough joint[J].Journal of Geophysics and Engineering,2013,10(4):45015-45023.

[21] 梁涛,常毓文,郭晓飞,等.巴肯致密油藏单井产能参数影响程度排序[J].石油勘探与开发,2013,40(3):357-362.

LIANG Tao, CHANG Yuwen, GUO Xiaofei, et al. Influence factors of single wells productivity in the Bakken tight oil reservoir[J].Petroleum Exploration and Development,2013,40(3):357-362.