直升机桨叶连续后缘襟翼设计与气动影响分析
2018-05-31李贇董凌华周金龙杨卫东
李贇,董凌华,周金龙,杨卫东
(南京航空航天大学 直升机旋翼动力学国家重点实验室,南京 210016)
0 引 言
主动控制后缘襟翼(Active Controlled Flap,简称ACF)智能旋翼技术是直升机发展的重要方向之一,其原理是通过主动调节旋转桨叶气动力在桨盘上的分布,从而降低旋翼振动载荷,提升直升机的性能。
国内外对该技术展开了广泛的研究。国外比较成功的ACF旋翼试验有F.K.Straub等[1-2]的SMART旋翼试验、E.Muir等[3]的旋翼塔试验以及P.Lorber等[4]的旋翼风洞试验,这些试验都取得了良好的减振效果。O.Dieterich等[5-6]对带后缘襟翼的BK-117直升机进行了飞行试验,平飞时,4阶桨榖力减小50%~90%。国内,张柱等[7]对智能旋翼技术展开了研究,设计的双X压电驱动机构可实现激振频率为18 Hz时后缘襟翼输出7.8°的偏角;刘士明等[8]进行的后缘襟翼减振仿真得到约50%的减振效果。上述研究成果证明了主动控制后缘襟翼能够有效地降低直升机的振动水平。
在早期,主要是基于分离式的后缘襟翼开展直升机旋翼减振主动控制研究,即襟翼是在桨叶加工之后安装上去的,会在桨叶表面留下缝隙,而且后缘襟翼多是由压电片、压电堆等驱动,这些驱动装置结构重量大,会增加桨叶的动力学设计难度。压电纤维复合材料(Macro Fiber Composite,简称MFC)的出现为主动控制后缘襟翼的发展带来了新的技术解决途径[9],MFC不仅具有良好的驱动能力,而且其厚度薄、重量轻、强度高,具有一定的韧性,能够布置于曲面结构中,对结构的影响较小。
本文将MFC作为后缘襟翼的驱动材料,基于NACA23012翼型设计连续后缘襟翼(Continuous Trailing-edge Flap,简称CTEF),采用热弹性比拟法和有限元方法分析CTEF在电场作用下的驱动效果,采用流固耦合方法计算桨叶段后缘襟翼偏转对剖面翼型气动特性的影响。
1 基于热弹比拟法的压电纤维复合材料建模
MFC是由NASA开发的一种智能材料,可作为作动器或传感器,具有良好的力学特性和可靠性。MFC的结构如图1所示[10]。

图1 MFC的结构组成
与传统的压电陶瓷相比,MFC有众多优点[11]:MFC强度高、韧性大,不容易出现脆性断裂;叉指电极电场方向沿着纤维的纵向覆盖了整个压电层,使MFC具有更高的d33压电常数和机电耦合系数,能够产生相对更大的驱动力和输出位移;MFC厚度薄、重量轻,能够粘贴在曲面上,对结构影响小,易于集成化设计。
为了简化MFC力学性能的分析计算,本文采用热弹比拟法[12-13]来模拟其逆压电效应。P1类型的MFC利用压电材料的d33效应,压电材料沿三方向极化,在自由边界条件下,由三方向的电场E3引起的应变为
εE=dE3=[d31d31d330 0 0]TE3
(1)
(2)
式中:εE为压电应变向量;d为压电常数向量;U为驱动电压;t为叉指电极相邻正负极之间的距离。
而热弹性体在自由边界条件下受温度载荷时,由内部温度变化引起的应变为
εE=αT=[α11α22α33α23α31α12]TT
(3)
式中:εE为热应变向量;α为热膨胀系数向量;T为温度增量。
比较式(1)和式(3),压电材料的压电应变方程和热弹性材料的温度应变方程相似,可将正交各向异性的压电材料驱动电压载荷比拟为温度载荷,定义:
(4)
(5)
(6)
α23=α31=α12=0
(7)
T=U
(8)
因此,压电材料的压电应变比拟为热弹性体的温度应变:
(9)
式(9)表明,对于压电材料仿真分析,可采用热弹性分析法将电场作用下的应变比拟为正交各向异性材料的热弹性应变。
为了验证本文采用的热弹性比拟法的有效性,开展MFC悬臂梁结构的压电应变实验,实验现场照片如图2所示,仿真和实验条件如表1所示。

图2 MFC悬臂梁结构压电应变实验

材 料参 数数 值M2814-P1悬臂梁钢片长度/mm38(有效28)宽度/mm20(有效14)厚度/mm0.3电极距/mm0.5杨氏模量/GPaE1=E2=15.86E3=30.34剪切模量/GPa5.51泊松比μ12=0.31μ13=μ23=0.16压电系数/(pm·V-1)d33=4.6×102d31=-2.1×102热弹比拟系数/(m·C-1)α33=9.2×10-7α11=α22=-4.2×10-7长度/mm80宽度/mm20厚度/mm0.5杨氏模量/GPa200剪切模量/GPa76.92泊松比0.3
热弹比拟法实验验证与修正如图3所示。

图3 热弹比拟法实验验证与修正
MFC的有限元计算结果呈线性趋势,这是由于热弹比拟法忽略了局部电场作用下的非均匀性。另外,计算结果的斜率略小于实验结果的斜率,为此,通过引入一个修正系数K进行修正,令
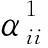
(10)
基于实验修正得到K=1.087,修正后计算值和实验值吻较好,表明采用热弹比拟法对MFC驱动器进行力学性能分析是可行的。
2 基于压电纤维驱动的连续后缘襟翼设计
与常规的后缘襟翼不同,CTEF与桨叶形成一个整体结构,利用材料的柔性,在MFC的驱动作用下,CTEF桨叶后缘实现连续变形。CTEF在电压驱动下的变形如图4所示(其中,+1 500/-500 V表示粘贴在基体上/下表面MFC的驱动电压)。
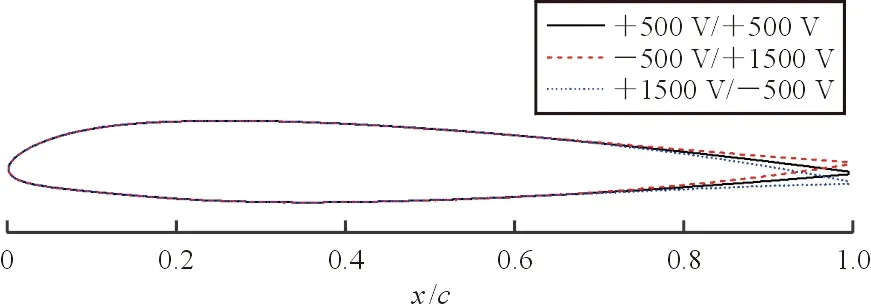
图4 后缘襟翼变形(Ma=0.5,α=6°)
CTEF剖面结构如图5所示,基于NACA23012翼型开展了CTEF与桨叶的集成设计,翼型弦长270 mm,襟翼从0.426倍弦长开始,沿翼型中弧线延伸到桨叶后缘。基体采用阶梯缩进的楔形结构,相邻两层高度差与MFC厚度一致,避免在粘贴过程中产生间隙,基体前缘部分包裹在桨叶大梁上,由玻璃纤维布压制而成,0.448倍弦长处厚度为3 mm,后缘处厚度减小为0.332 mm。在基体的上/下表面各粘贴四层型号为M8557-P1的MFC压电作动器,相邻两层之间错位分别为16、12、8 mm。若要襟翼下偏,上方的MFC施加正电压,下方的MFC施加负电压,驱动翼剖面后缘产生向下的弯曲变形;反之,翼剖面后缘向上弯曲。
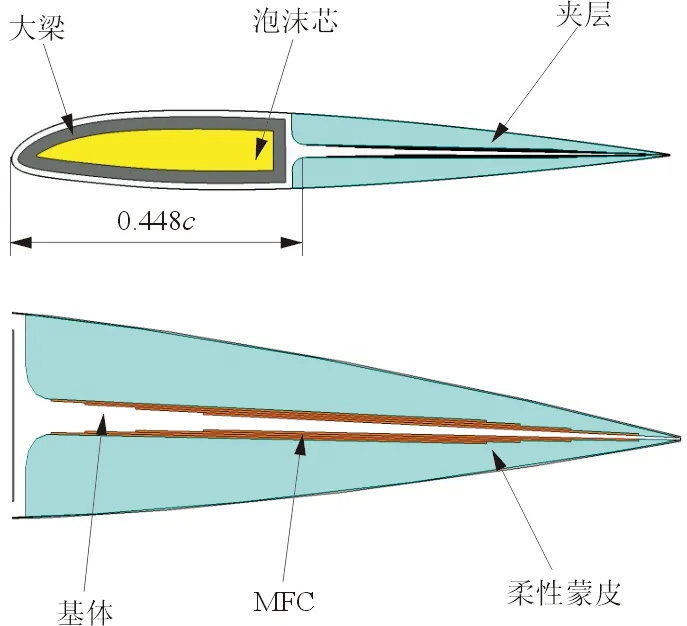
图5 CTEF剖面结构
合理选取后缘各部分的材料是CTEF设计的重要环节之一。本文针对多种材料的夹层和蒙皮进行后缘偏转位移的计算分析,各材料的弹性模量如表2所示,蒙皮厚度为0.2 mm。

表2 夹层和蒙皮的材料及弹性模量
在+1 500 V/-500 V驱动电压下,夹层和蒙皮材料不同时CTEF的后缘位移的计算结果如表3所示。
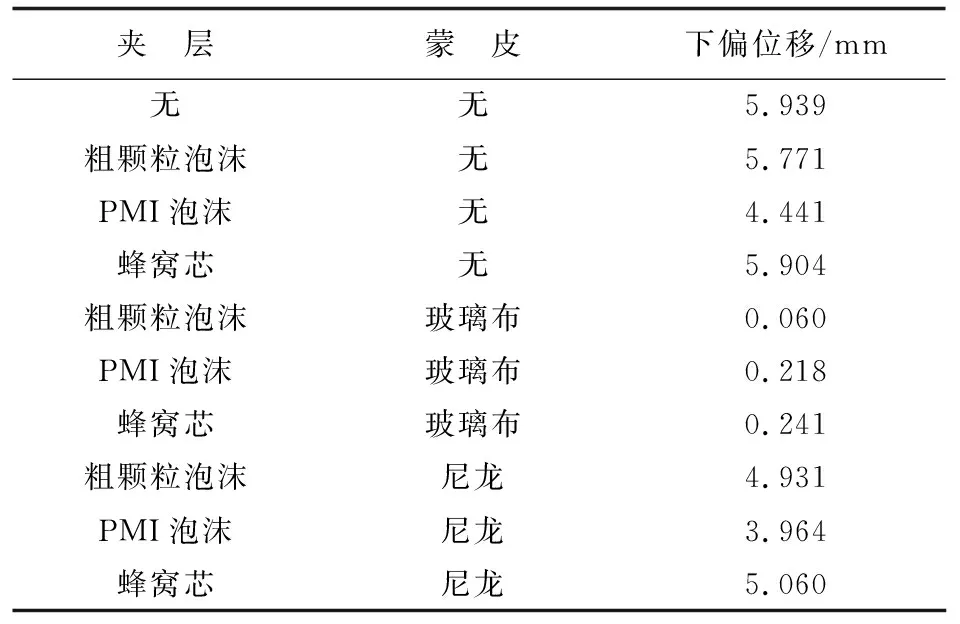
表3 加+1 500 V/-500 V电压,不同夹层和蒙皮下CTEF的后缘尖端位移
从表3可以看出:粘贴在MFC作动器上的泡沫夹层和蒙皮对后缘襟翼变形的抑制作用明显。由于玻璃布蒙皮刚度大,MFC作动器驱动后缘襟翼不会发生明显的变形,因此,蒙皮应具有较好的柔性,这不仅有利于襟翼的变形,还可以防止交变载荷作用下疲劳分层失效。同时,夹层材料应在厚度方向应具有较大的抗压刚度,同时剪切刚度要尽量小。
通过对比几种不同材质的夹层和蒙皮对襟翼偏转的影响,分别选择蜂窝芯和尼龙作为夹层和蒙皮的材料。无气动载荷时,在+1 500/-500 V电压驱动下后缘尖端下5.06 mm,在-500/+1 500 V电压驱动下后缘尖端上5.01 mm,实现了有效的位移输出。
3 连续后缘襟翼气动影响分析
3.1 流固耦合方法
由于CTEF的变形,不能用一个确定的转轴和偏转角描述,因此,本文采用流固耦合方法[10,14]分析连续可变后缘襟翼的气动效果。
流固耦合方法基于ANSYS Workbench平台,调用Fluent软件计算气动力,载荷作用下的结构响应调用Mechanical模块求解,流体和结构之间的耦合通过System Coupling模块来实现,它保证了气动力求解和结构响应求解同时进行,在每一个时间步结束后,都要进行耦合面的信息交换,实现结构响应和气动力的实时耦合。
考虑到CTEF的变形,必须用到网格更新技术,滑移网格对襟翼刚性偏转的流场模拟较好,但是不能用于后缘连续可变襟翼,而动网格可以应对任意复杂的变形,Fluent非定常气动力计算的重点和难点集中于网格运动问题。
动网格(Dynamic Mesh)通常包含两方面的内容:运动区域指定以及网格更新方法。运动区域的指定,对于可用数学语言描述的运动通常采用Profile或者UDF(User-defined Functions)宏定义,而对于无法用数学表达式描述的连续可变襟翼的运动,结构变形的位移完全依赖于System Coupling读取Mechanical求解的结构响应,则只需要指定CTEF表面为耦合运动方式,流场网格的更新由程序自动控制。Fluent提供的众多网格更新方法中:光顺(Smoothing)方法的应用范围最广,光顺方法又分为弹簧光顺(spring)和扩散光顺(diffusion),弹簧光顺适用于变形较小的情况,相对于翼型附面层极密的网格,CTEF变形较大,采用弹簧光顺容易出现负体积,而扩散光顺通常可以将变形扩散到更远的区域,与弹簧光顺相比,还可以得到更好的网格质量,因此本文采用扩散光顺的网格更新方法。
扩散光顺通过求解以下扩散方程来设置网格节点的位置:

(11)
(12)
式中:xold为网格更新前节点位置向量;xnew为网格更新后节点位置向量;u为网格的运动速度,求解出运动速度后,可以很容易获得网格节点在下一个时间步长的位置;γ为扩散系数,扩散系数的计算有两种方法,式(13)是基于网格节点与边界之间的距离计算扩散系数,式(14)是基于网格体积计算扩散系数。
(13)
(14)
式中:d为正则化后的网格节点与边界之间的距离;V为网格正则化体积;α为扩散光顺方法要设置的参数,取值范围为0~3。当α=0时,γ≥1,则计算域中的网格均匀扩散,提高此参数可以使距离运动边界较远区域吸收更多的位移,本文取中间值1.5。
流固耦合的计算流程如图6所示。其中:n为当前时间步数;N为总时间步数;i为每个时间步的当前迭代次数;I为每个时间步的最大迭代次数;F为Fluent求解的气动力;S为Mechanical求解的结构响应。

图6 流固耦合流程图
3.2 连续后缘襟翼偏转效果分析
基于材料设计参数影响分析的结果,确定CTEF桨叶段各部分的材料,其主要参数如表4所示。利用流固耦合方法计算迎角和马赫数对襟翼后缘偏转的影响。

表4 连续后缘襟翼各部分材料及主要参数
CTEF通常布置在桨叶0.75倍旋翼半径附近,直升机悬停状态下,该处来流速度约为0.5Ma。来流速度为0.5Ma时, +1 500 V/-500 V电压驱动下,后缘位移随迎角的变化情况如图7(a)所示,可以看出:随着迎角增大,后缘位移逐渐减小。迎角为6°,+1 500 V/-500 V电压驱动下,后缘位移随来流速度的变化情况如图7(b)所示,可以看出:随着来流速度增大,后缘位移也会减小,相对于剖面来流速度,剖面迎角对CTEF偏角影响要小。
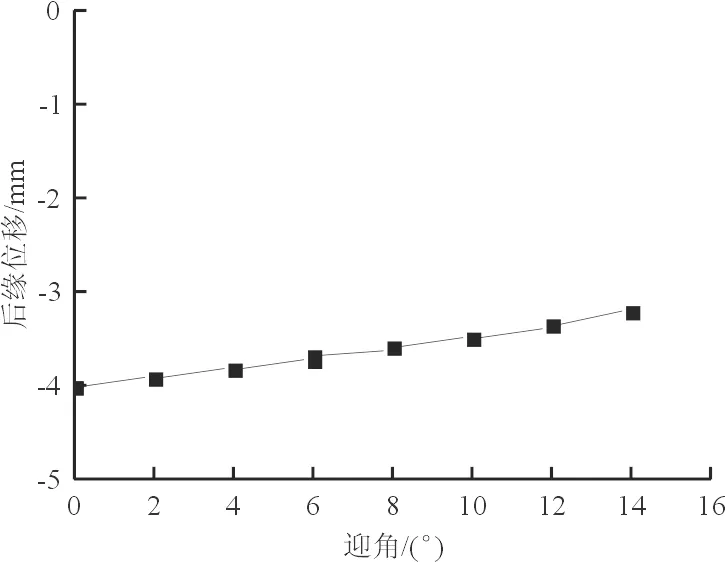
(a) Ma=0.5

(b) α=6°
计算带CTEF的翼剖面在来流速度为0.5Ma,雷诺数为3.14×106,迎角分别为0°和6°条件下,连续后缘襟翼分别在基准电压+500 V/+500 V、下偏电压+1 500 V/-500 V、上偏电压-500 V/+1 500 V时翼剖面的压力系数,以及偏转对升力、阻力、力矩系数的改变。不同计算条件下,后缘不偏转与偏转的压力云图如图8~图9所示。
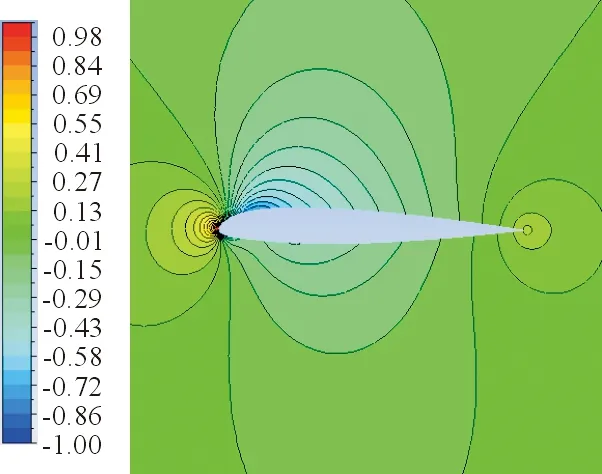
(a) +500 V/+500 V

(b) +1 500 V/-500 V

(c) -500 V/+1 500 V
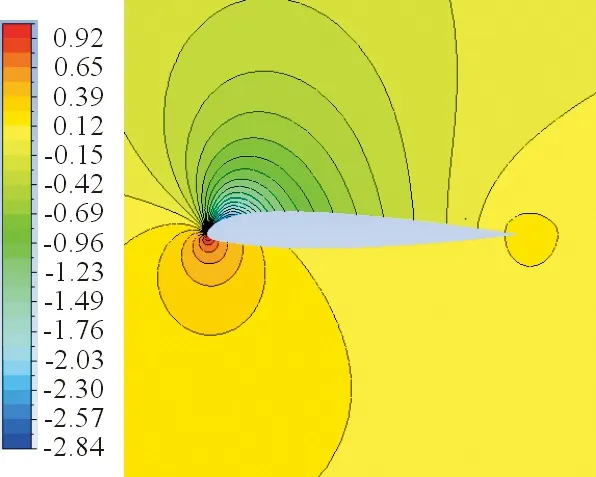
(a) +500 V/+500 V
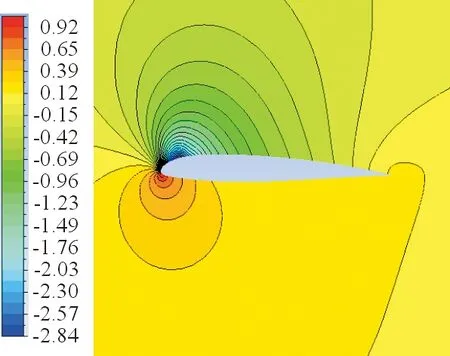
(b) +1 500 V/-500 V
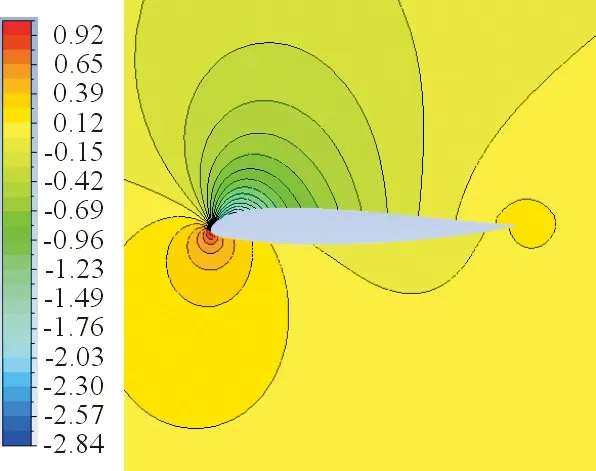
(c) -500 V/+1 500 V
从图8~图9可以看出:襟翼下偏,翼型上表面的低压区明显增大;襟翼上偏,翼型下表面高压区明显缩小。
CTEF对翼剖面压力分布的影响如图10所示,可以看出:当桨叶后缘下偏时,剖面压差增大,上偏时,剖面压差降低;压力系数曲线保持光滑,表明气动载荷下CTEF保持良好的气动外形。
来流速度为0.5Ma,0°和6°迎角下后缘偏转对升力系数、阻力系数、力矩系数以及升阻比的影响如表5所示。

(a) α=0

(b) α=6°

迎角上/下表面MFC的驱动电压/V尖端偏转/mmCLCDCMCL/CD+500/+500 0.123 0.1420.009 38-0.007 90 15.14α=0+1 500/-500-4.109 0.3970.010 13-0.049 96 39.19-500/+1 500+4.323-0.1110.009 45 0.033 94-11.75+500/+500 0.448 0.8640.014 55 0.004 93 59.38α=6°+1 500/-500-3.799 1.1050.017 88-0.030 33 61.80-500/+1 500+4.899 0.6210.012 03+0.042 89 51.62
从表5可以看出:连续后缘襟翼的小幅变形即会对翼剖面升力和力矩产生显著影响,但对翼剖面气动力阻力影响较小。
3.3 不同后缘偏转对翼剖面气动特性的影响
进一步开展CTEF偏转对翼剖面气动特性的影响分析。计算条件为:带CTEF的NACA23012翼型,弦长270 mm,来流速度分别为0.5Ma、0.7Ma,驱动电压从-500 V/+1 500 V到+1 500 V/-500 V,电压变化间隔为250 V。计算结果如图11~图12所示。可以看出:在失速以前,同一迎角下,连续后缘襟翼变形所导致的升力系数的变化量约0.5,力矩系数的变化量约0.08,阻力系数一直保持较低水平;在直升机桨叶工作迎角、马赫数范围内,驱动电压变化对气动系数变化的规律性明显,表明连续后缘襟翼对翼剖面气动力具有良好的控制效果。

(a) 升力系数
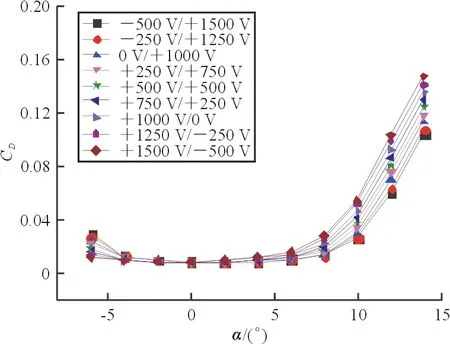
(b) 阻力系数
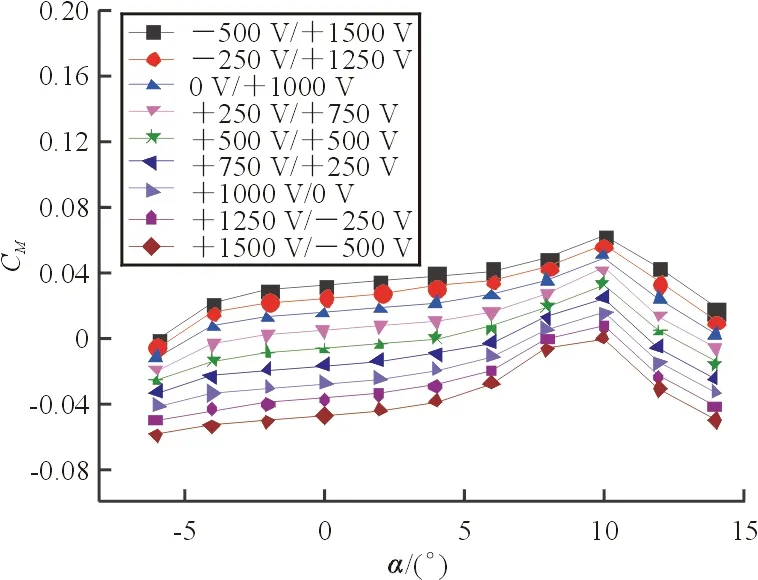
(c) 力矩系数

(a) 升力系数

(b) 阻力系数
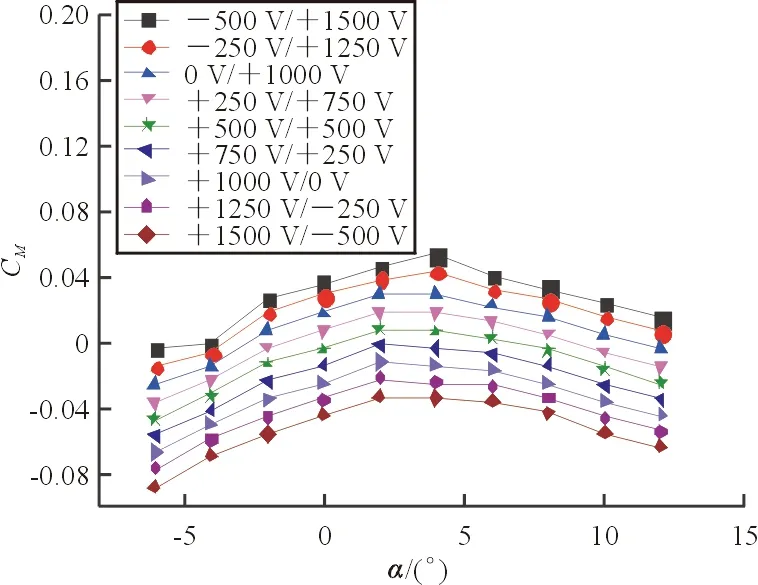
(c) 力矩系数
4 结 论
(1) 本文基于MFC设计了可用于直升机桨叶的连续后缘襟翼,通过实验修正建立了MFC的热弹比拟法力学分析模型;基于ANSYS Workbench平台,采用流固耦合方法研究了连续后缘襟翼的驱动效果以及偏转对气动特性的影响。
(2) 通过对连续后缘襟翼合理的结构设计和选材设计,MFC作动器具有驱动后缘襟翼有效变形的能力。
(3) 采用连续后缘襟翼可以显著影响翼剖面的气动升力和力矩,同时对阻力影响较小,表明连续后缘襟翼具有应用于旋翼减振控制的潜力。
[1] Straub F K, Kennedy D K, Stemple A D, et al. Development and whirl tower test of the SMART active flap rotor[C]. Proceedings of SPIE, 2004, 5388: 202-212.
[2] Straub F K, Anand V R, Birchette T S, et al. Smart rotor development and wind tunnel test[C]. Germany: Proceedings of the 35th European Rotorcraft Forum, 2009, 413-430.
[3] Muir E, Liu L, Friedmann P P, et al. Hysteresis characterization in piezoceramic stack actuators and its influence on vibration and noise reduction in helicopters using actively controlled flaps[C]. AIAA-2010-2994, 2010.
[4] Lorber P, O’Neill J, Hein B, et al. Whirl and wind tunnel testing of the Sikorsky active flap demonstrator rotor[C]. Virginia Beach: American Helicopter Society 67th Annual Forum, 2011.
[5] Dieterich O, Enenkl B, Roth D. Trailing edge flaps for active rotor control aeroelastic characteristics of the ADASYS rotor system[C]. Netherlands: American Helicopter Society 62nd Annual Forum, 2006.
[6] Roth D, Enenkl B, Dieterich O. Active rotor control by flaps for vibration reduction full scale demonstrator and first flight test results[C]. Netherlands Proceedings for the 32nd European Rotorcraft Forum, 2007, 801-814.
[7] 张柱, 黄文俊, 杨卫东. 后缘小翼型智能旋翼桨叶模型设计分析与试验研究[J]. 南京航空航天大学学报, 2011, 43(3): 296-301.
Zhang Zhu, Huang Wenjun, Yang Weidong. Design analysis and test of smart rotor blades model with trailing edge flaps[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(3): 296-301.(in Chinese)
[8] 刘士明, 杨卫东, 虞志浩, 等. 后缘小翼智能旋翼有限偏角减振效果分析[J]. 振动、测试与诊断, 2017, 37(3): 432-439.
Liu Shiming, Yang Weidong, Yu Zhihao, et al. Vibration control analysis of trailing edge flap smart rotor with limited deflection angle[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(3): 432-439.(in Chinese)
[9] Shen Jinwei, Robert P, Liu Yi, et al. Design and optimization of an airfoil with active continuous trailing-edge flap[C]. Phoenix: American Helicopter Society 69th Annual Forum, 2013.
[10] 朱红钧. ANSYS 14.5热流固耦合实战指南[M]. 北京: 人民邮电出版社, 2014: 342-365.
Zhu Hongjun. Practical guide for ANSYS14.5 heat fluid-structure interaction[M]. Beijing: Posts and Telecommunications Press, 2014: 342-365.(in Chinese)
[11] 侯志伟, 陈仁文, 徐志伟, 等. 压电纤维复合材料在结构减振中的应用[J]. 振动测试与诊断, 2010, 30(1): 51-54.
Hou Zhiwei, Chen Renwen, Xu Zhiwei, et al. Application of macro-fiber composite to structural vibration suppression[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(1): 51-54.(in Chinese)
[12] 董兴建, 孟光. 压电结构的热弹性比拟建模方法[J]. 应用力学学报, 2005, 22(3): 346-350.
Dong Xingjian, Meng Guang. A thermo-elasticity analogy modeling method for piezoelectric structure[J]. Chinese Journal of Applied Mechanics, 2005, 22(3): 346-350. (in Chinese)
[13] 孙士勇, 杨睿, 张少辉, 等. 叉指形电极压电执行器的热弹性比拟分析方法[J]. 压电与声光, 2015, 37(1): 32-34.
Sun Shiyong, Yang Rui, Zhang Shaohui, et al. The thermo-elasticity analogy approach for the analysis of Inter-digital electrodes of piezo-actuator[J]. Piezoelectrics & Acoustooptics, 2015, 37(1): 32-34.(in Chinese)
[14] Giannelis N F, Vio G A. Computational benchmark of commercial fluid-structure interaction software for aeroelastic applications[C]. Saint Petersburg: AIAC16 Australian International Aerospace Congress, 2015.
