不同海浪谱激励下矩形液舱内液体晃荡试验研究

薛 米 安， 陈 奕 超， 苑 晓 丽， 邢 建 建

( 1.海岸灾害及防护教育部重点实验室(河海大学)， 江苏 南京 210098；2.河海大学 港口海岸与近海工程学院， 江苏 南京 210098；3.河海大学 理学院， 江苏 南京 210098 )

0 引 言

海洋中蕴藏着全球70%的油气资源，随着我国能源需求的急剧增加，开发深海油气资源成为我国能源增量的主要途径之一．为了确保油气资源在海洋中的安全运输，减少不必要的经济损失及原油泄漏等灾害的发生，有必要对与原油和液化天然气运输紧密联系的液体晃荡问题进行深入研究，因为该问题直接影响着充液容器的结构安全及海洋中液货船舶航行的稳定性．

近年来，晃荡问题尤其是简谐激励下的液体晃荡被广泛关注[1-4]．事实上海浪、地震波等都属于不规则波，深入研究不规则波激励下的液体晃荡特性，以及相关的水动力学问题具有更重要的工程应用价值．针对液体晃荡问题，目前的研究方法主要有3种：基于势流假设的理论分析、基于尺度物理模型的试验研究和基于求解各类流体控制方程的数值模拟．在理论分析方面，Chen等[5]基于势流理论研究了地震波激励下的大幅度液体晃荡．然而，在实际的工程应用中，液体晃荡一般会非常剧烈，特别是在极端条件下液体自由面会发生破碎而表现出强烈的非线性特性，再加上自由面的时变性，理论分析受到了限制．模型试验被认为是最能够准确描述液体晃荡现象的一种方法，Nasar等[6]通过模型试验研究了驳船上充液容器在不规则波激励下的晃荡压力分布．蒋梅荣等[7]基于振动台试验研究了简谐激励下弹性侧壁液舱内的共振晃荡特性．但是由于模型试验存在尺度效应等问题，再加上试验装置的昂贵价格，数值模拟成为研究晃荡问题最常用的方法．

朱仁庆等[8]基于CFD技术，提出了LNG船薄膜型液舱晃荡压强的数值预报方法并和模型试验结果进行了对比，结果显示所建立的数值模型能够有效地预报LNG船液舱晃荡荷载．此外，李文刚等[9]利用有限元模型研究了水平地震激励下的储罐液体晃荡．Zama等[10]研究了在地震波作用下，地面长时间振动所诱发的液体晃荡对石油储罐的破坏．Ikeda等[11]通过求解Laplace方程，研究了圆柱形容器内液体晃荡对结构物非线性随机响应的影响．Wang等[12]基于全非线性波浪势流理论采用有限元法，分析了二维矩形容器在随机激励下的液体晃荡现象．Sriram等[13]通过求解Laplace方程，数值研究了水平和垂向随机激励下的二维晃荡波．Chen等[14]通过求解二维不可压欧拉方程，研究了海浪诱导下浮式容器中的全非线性液体晃荡现象，以及晃荡流体对浮体运动的影响．邓棋等[15]基于OpenFOAM开源代码采用超谐共振稳态解作为外部激励，研究了船舶在超谐共振横摇条件下的晃荡特性，发现在此条件下自由液面容易出现翻卷、破碎等强非线性现象，舱壁压力历时曲线表现出多峰值特征，且峰值要远大于简谐激励的情况．

综上所述，随机激励下的液体晃荡及其相关的水动力学问题，逐渐受到各国研究人员的重视．然而目前随机激励下的晃荡研究还鲜有涉及不同谱型对液体晃荡影响的讨论．当具有相同谱峰周期和有效波高时Bretschneider谱和JONSWAP谱的能谱密度函数具有较大的不同，前者波浪能量在频域上的分布相对分散，谱形较平缓，属于典型的宽频带谱；后者波浪能量在频域上的分布相对集中，谱形较尖锐，离散度高，属于典型的窄频带谱．为进一步探索不同随机海浪谱激励下的液体晃荡统计特征，本研究以典型的宽频带Bretschneider谱和窄频带JONSWAP谱两种谱，分别作为输入谱驱动液体晃荡平台作随机运动，比较分析不同随机运动激励下矩形液舱内晃荡波高、自由液面形状及晃荡压力随谱峰周期和有效波高的变化规律，为不同海域中液货船舶航行的稳定性，以及液舱结构安全设计提供有益的参考和借鉴．

1 试验设置

1.1 随机运动模拟平台

利用不规则波造波机建立了如图1所示的液体晃荡试验平台并组建了相应的测量系统[16-17]．压力传感器、浪高仪、摄像机、位移传感器分别被用于测量液体在随机晃荡过程中的砰击压力和自由液面高程、形状及液舱的运动位移等物理量随时间的变化规律．数据采集系统被用于保存并实时显示各个传感器的测量数据．该试验平台可被用于开展JONSWAP谱和Bretschneider谱等各种随机海浪谱所生成随机运动激励下的液体晃荡特性研究．

图1 液体晃荡试验装置示意图Fig.1 Sketch of experimental rig for liquid sloshing

JONSWAP谱的表达式如下：

γexp[-(Tpf-1)2/2σ2]

(1)

(2)

(3)

(4)

Bretschneider谱的表达式如下：

(5)

其中ωp为谱峰频率．

通过不规则波造波机可将海浪谱转化成如下的随机运动位移：

(6)

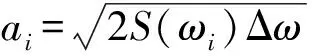
1.2 液舱模型及测量仪器布置

试验中矩形液舱的长度L=0.57 m，宽度W=0.31 m，高度H=0.70 m．该液舱由6 mm厚的透明有机玻璃板制作而成．浪高仪及压力传感器的布置如图2所示，两只浪高仪分别布置在离矩形液舱左右侧壁10 mm位置处并被固定在液舱上，4只压力传感器依次安装在液舱右壁离水箱底部65、105、145和185 mm处．液舱内的液体深度h=0.18 m保持不变．液体为室温下的自来水．

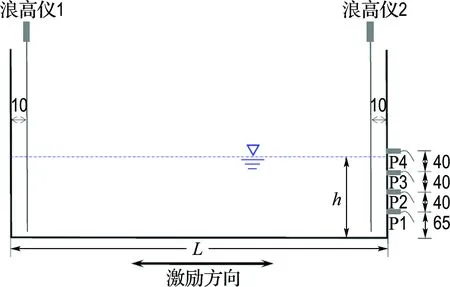
图2 压力传感器及浪高仪的试验布置(单位:mm)Fig.2 The experimental layout of wave gauges and pressure transducers (unit: mm)

对于液深为h、长度为L的二维矩形容器，根据线性波浪理论推导出的色散方程可求得固有频率

(7)

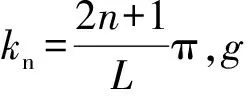
不知过了多久，渐入梦境的王树林被一阵波动惊醒，有人掀起被角从他的脚畔钻了进来。像一条湿滑的鱼。是辛娜，浴后的辛娜光着身子钻到了王树林的胸前，不由分说滚烫地咬住了王树林的嘴唇。王树林的鼻息间，酒气弥漫。

1.3 试验工况

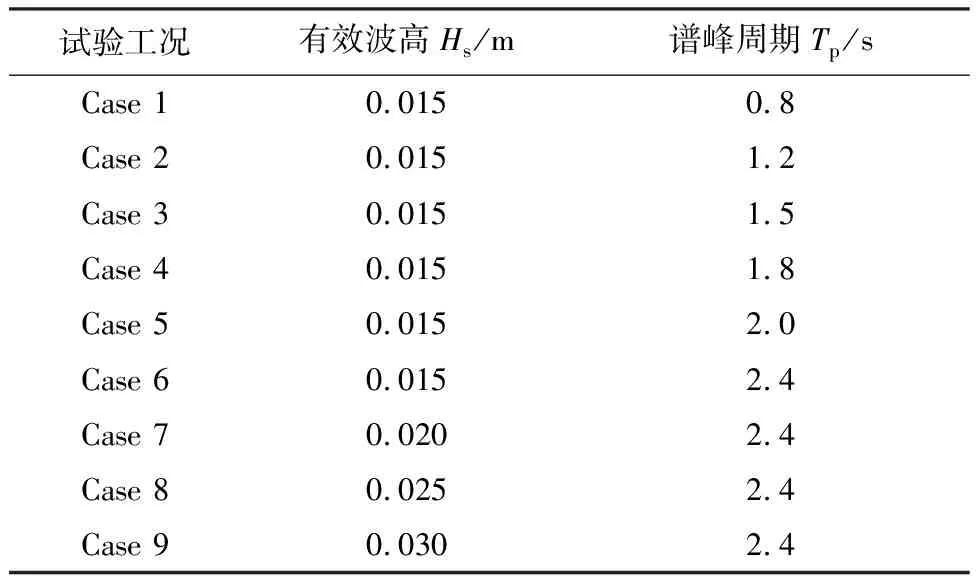
对海浪谱来说，给定有效波高和谱峰周期，即可确定频谱密度随频率的变化关系，从而根据方程(6)便可以通过造波机利用位移传感器测得与推波板相连的液体晃荡试验平台的随机运动位移曲线．在试验中，采用的两种海浪谱的9组有效波高和谱峰周期如表1所示．

在9组工况下，除非有特殊说明，试验持续时间均为40 s．在40 s内由位移传感器测得的两种海浪谱作用下液体晃荡试验平台的冲程ds随有效波高和谱峰周期的变化规律如图3所示．从图3(a)中可以看出两种海浪谱作用下液体晃荡试验平台的水平冲程随谱峰周期的增加尽管有减小的趋势但并不是单调减小．但当有效波高为0.015 m且谱峰周期为1.2 s时，JONSWAP谱作用下的试验平台水平冲程均明显大于其他试验工况．图3(b)显示试验平台的水平冲程随有效波高的增加而增大，且两种海浪谱作用下的水平冲程相差较小．

表1 Bretschneider谱和JONSWAP谱的9组有效波高及谱峰周期

Tab.1 Significant wave height and peak period of Bretschneider and JONSWAP spectra

试验工况有效波高Hs/m谱峰周期Tp/sCase 1Case 2Case 3Case 4Case 5Case 6Case 7Case 8Case 90.0150.0150.0150.0150.0150.0150.0200.0250.0300.81.21.51.82.02.42.42.42.4

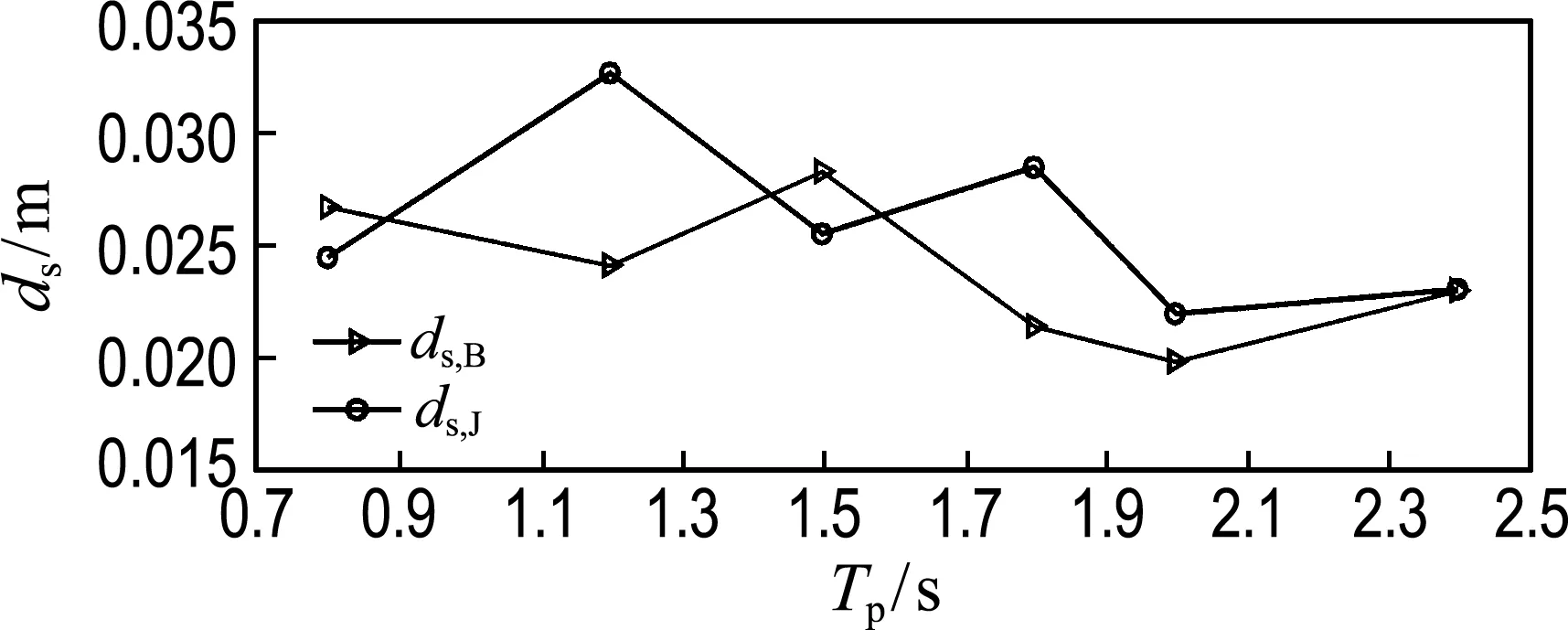
(a) 随谱峰周期变化

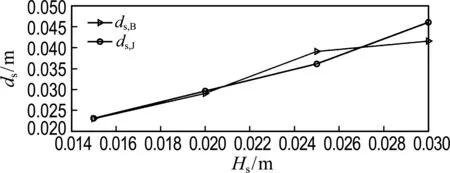
(b) 随有效波高变化

图3 Bretschneider谱与JONSWAP谱作用下液体晃荡试验平台的冲程随有效波高和谱峰周期的变化关系

Fig.3 The stroke of shaker table varying with significant wave height and peak period of Bretschneider spectrum and JONSWAP spectrum

2 结果与讨论

2.1 自由液面高程

当有效波高Hs=0.015 m并保持不变时，图4(a)给出了Bretschneider谱与JONSWAP谱激励作用下液体晃荡最大自由液面高程与谱峰周期的关系．从图4(a)中可以看出，在两种海浪谱作用下，矩形液舱内浪高仪1和浪高仪2测点处液体晃荡自由液面高程的最大值基本上随着谱峰周期的增加而减小．由色散方程(7)可求得当液体深度h=0.18 m时，充液舱的固有周期T0=0.98 s．随着谱峰周期的增加，海浪谱的峰值频率逐渐偏离充液舱的最小固有频率，因此使得液体晃荡的自由液面高程也逐渐减小．Case 2中，在Bretschneider谱作用下浪高仪2处具有较大的最大自由液面高程，主要原因是此工况中的谱峰频率接近充液舱的固有频率，导致强非线性晃荡现象的发生．

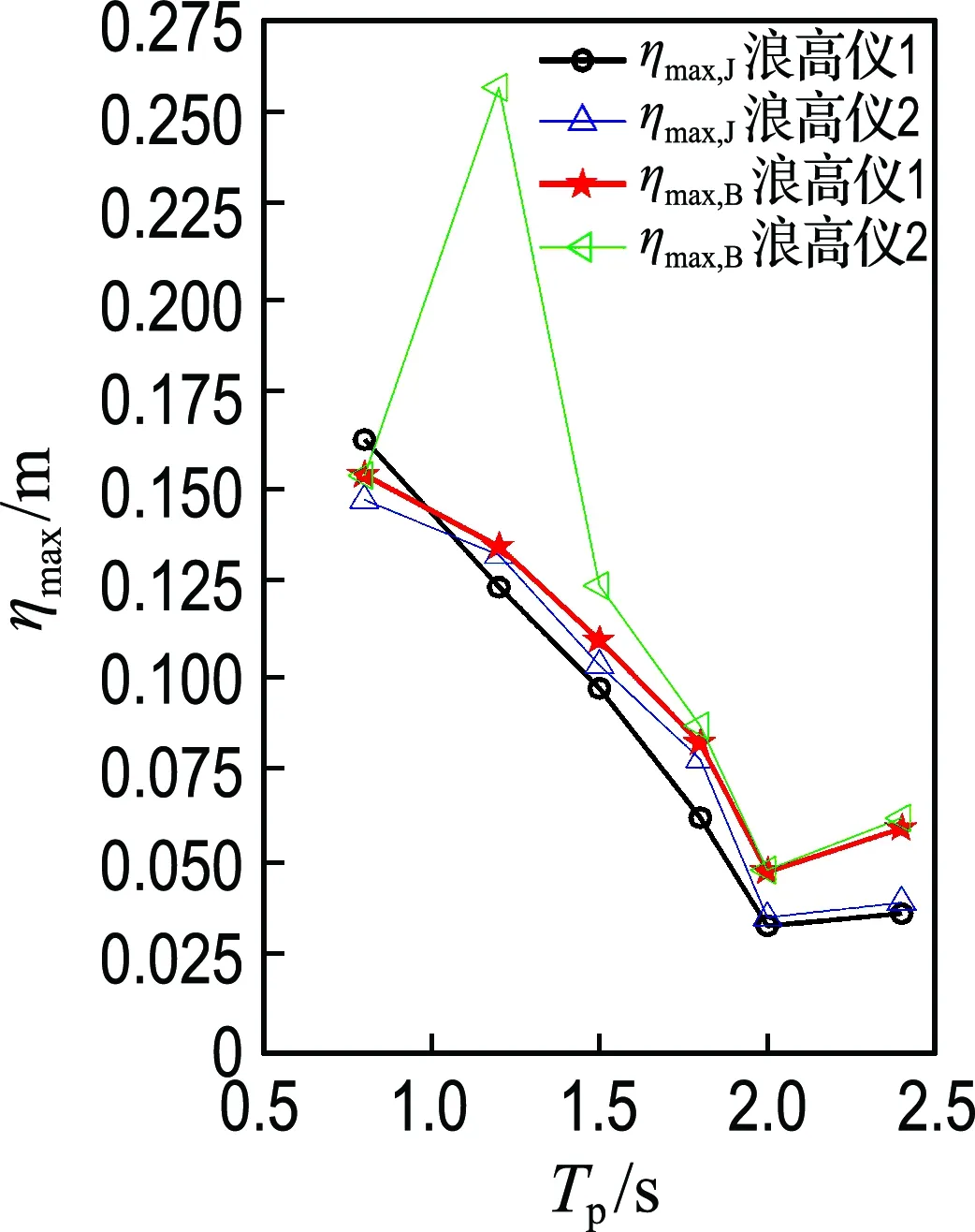
(a) 随谱峰周期变化

图4 Bretschneider谱与JONSWAP谱激励作用下液体晃荡最大自由液面高程随谱峰周期及有效波高的变化规律

Fig.4 Relation between the maximum free surface elevation of liquid sloshing and peak period，significant wave height excited by Bretschneider spectrum and JONSWAP spectrum

当谱峰周期Tp=2.4 s并保持不变时，图4(b) 给出了Bretschneider谱与JONSWAP谱激励作用下，液体晃荡最大自由液面高程与有效波高的关系．由图4(b)可知，在两种海浪谱作用下，液舱内浪高仪1和浪高仪2测点处的自由液面高程最大值均随着有效波高的增加而增大．当两种海浪谱具有相同有效波高和谱峰周期时，由图4可观测到相同测点处Bretschneider谱作用下液体晃荡自由液面高程的最大值均稍大于JONSWAP谱激励作用下液体晃荡自由液面高程的最大值，因此液舱在Bretschneider谱作用下会产生更为剧烈的晃荡现象．

事实上，Bretschneider谱的能谱密度函数较JONSWAP谱平缓，属于宽带谱，能量密度在频域上的分布相对均匀．因而Bretschneider谱激励下，液舱内液体在较宽的频带内会获得更多的能量．当水深不变时，充液舱的最低固有频率f0=1.019 Hz也保持不变，在该频率下恰好Bretschneider谱的能量密度大于JONSWAP谱的能量密度．因此，如图5所示，试验工况为Case 1时，在Bretschneider谱作用下液舱内的液体具有较大的爬高．

为深入研究晃荡自由液面高程与海浪谱谱峰频率之间的关系，采用快速傅里叶变换对自由液面高程随时间的变化曲线进行了频域分析．如图6所示，给出了9组具有不同谱峰频率和有效波高的Bretschneider谱与JONSWAP谱激励下，浪高仪1处自由液面高程变化的能谱图．由图6可得，9种工况所对应的第一峰值频率依次为1.000、0.975、1.000、1.000、1.000、1.025、1.025、1.025 和1.025 Hz，其中Case 2有两个较显著的峰值频率依次为0.975和1.025 Hz，均较接近由色散方程(7)求得的充液舱的最低固有频率1.019 Hz，表明在此工况下液舱内液体产生了接近共振现象的剧烈非线性晃荡．从自由液面高程能谱图中看出，第一峰值频率均接近充液舱的最低固有频率，这表明自由液面波形的变化主要受液舱固有频率的调制．海浪谱激励下液舱内液体晃荡生成的自由表面波能量也主要分布在系统最低固有频率附近．海浪谱谱峰频率与谱型对受激晃荡波的能量在频率上的分布没有显著的影响．但是从图6中可知，当具有相同的有效波高和谱峰频率时，在Bretschneider谱生成的不规则运动的激励下，液舱内液体会受激产生较为剧烈的晃荡现象．

图5 Bretschneider谱和JONSWAP谱激励下液舱内左右两侧壁处晃荡波最大爬高位置比较

Fig.5 Comparisons of the maximum free surface profile at left and right tank walls excited by Bretschneider spectrum and JONSWAP spectrum respectively

2.2 动态压力分布

液体晃荡的关键问题是，确定极端条件下的最大晃荡冲击荷载和晃荡荷载的时间历程及其统计特性．晃荡荷载与自由液面的大幅度变化密切相关，预测由液体晃荡引起的极限压力荷载，对充液系统的结构强度设计，及对载有充液系统各种结构物的稳定性分析都具有十分重要的工程意义．为了研究有效波高、谱峰频率与谱型对液体晃荡冲击压力分布的影响，图7(a)给出了作用在水箱右侧壁不同位置处的最大动态压力与谱峰周期和谱型的关系．从图7(a)中可以得出，当有效波高等于0.015 m并保持不变时，受迫晃荡的液体对液舱右侧壁的最大冲击压力随着谱峰周期增加而减小．对于同一测点，海浪谱Bretschneider谱激励下的最大动态压力要比JONSWAP谱激励下的动态压力稍大，而且最大动态压力在液舱内壁上的分布从液舱底部到自由液面处依次增大，位于自由液面以上的压力测点P4的最大动态压力最大，表明越靠近自由液面，液舱内受迫晃荡的液体对液舱内壁的冲击荷载越大．

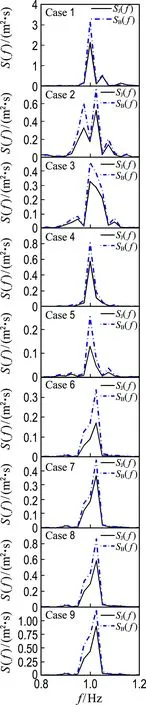
图6 不同有效波高和谱峰周期下不规则运动激励下浪高仪1处自由液面变化的能谱密度

Fig.6 Spectra density of free surface at the wave gauge 1 due to irregular wave excitation for different significant wave heights and peak periods

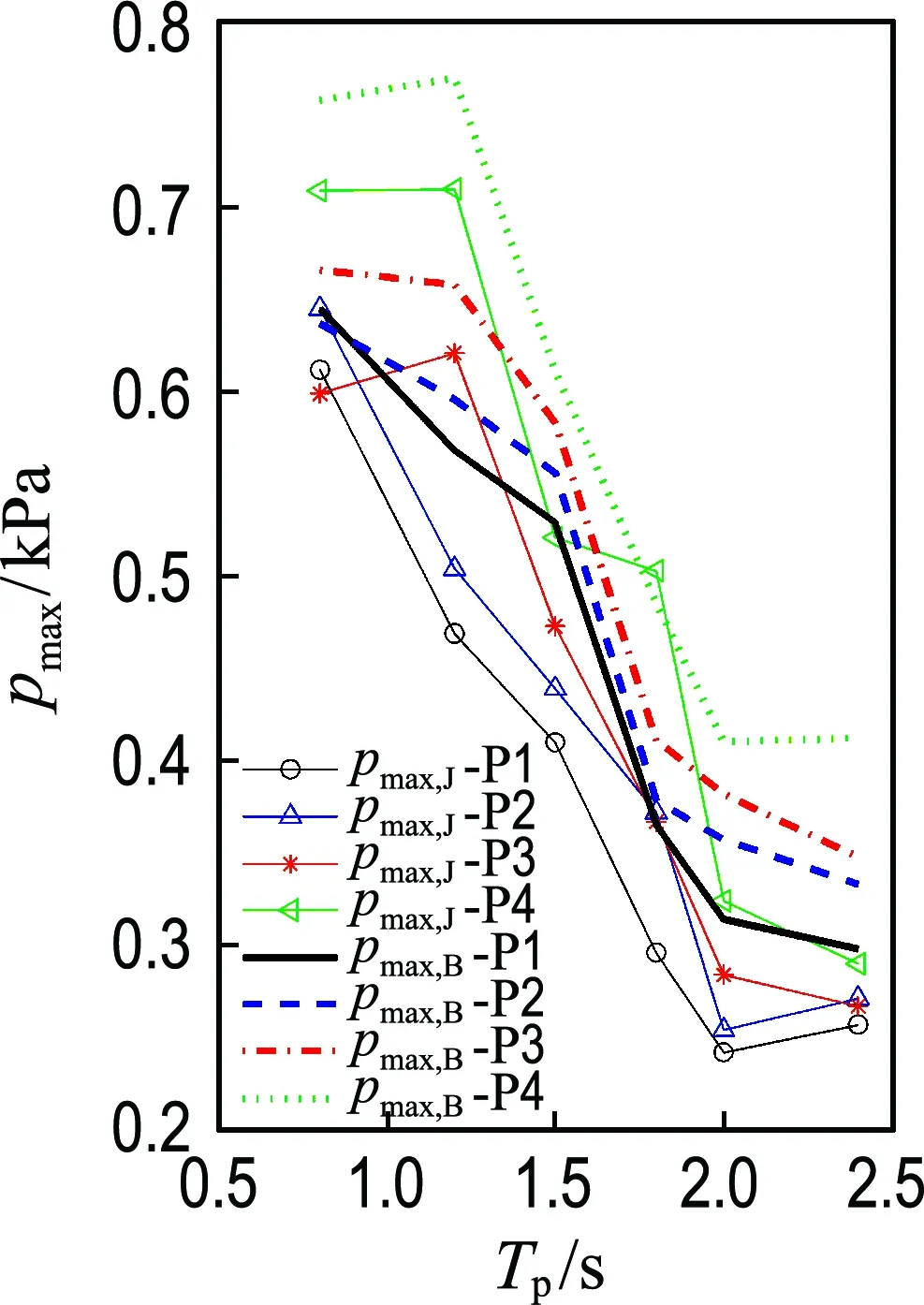
(a) 随谱峰周期变化

图7 Bretschneider谱与JONSWAP谱激励下液体晃荡最大动态压力与谱峰周期及有效波高的关系

Fig.7 Relation between the maximum dynamic pressure of liquid sloshing and peak period, significant wave height excited by Bretschneider spectrum and JONSWAP spectrum

图7(b)给出了作用在液舱右侧壁不同位置处的最大动态压力与有效波高和谱型的关系．从图7(b)中可看出当谱峰周期等于2.4 s并保持不变时，最大动态压力随着有效波高的增大而单调增大．对于同一压力测点，宽频带Bretschneider谱激励下最大动态压力比窄频带JONSWAP谱激励下最大动态压力大．动态压力在液舱内壁上的分布从液舱底部到自由液面附近依次增大，且位于自由液面以上的压力测点P4处的动态压力最大．从图7中也可以得出对于相同的波要素即有效波高和谱峰周期，Bretschneider谱作用下液舱右侧壁的最大动态压力要大于JONSWAP谱作用下的最大动态压力．对于自由液面以下的压力测点，作用在液舱右侧壁上的动态压力在最接近自由液面的P3位置处具有最大值，这是由于液舱在随机运动激励下，自由液面处的液体波动最为剧烈，导致晃动的液体与液舱内壁之间形成如图8所示的强烈砰击作用．

图8展示了Bretschneider谱(Case 1)作用下，液体晃荡波的演化过程及其与液舱内壁的相互作用．从图8中可以看出，随机海浪谱激励下的晃荡波属于典型的破碎行进波，当行进波传播到液舱内壁附近时，由于行进波波形传播速度大于液舱运动速度或行进波波形传播方向与液舱运动方向相反时，就会发生行进波撞击液舱内壁形成剧烈的波浪破碎乃至液滴飞溅等强非线性砰击作用．

图8 Bretschneider谱(Case 1)作用下液体晃荡波的演化及其与液舱内壁的相互作用Fig.8 Snapshots of the liquid sloshing wave and its interaction with tank wall excited by Bretschneider spectrum (Case 1)

3 结 语

通过改变有效波高和谱峰周期，分别研究了Bretschneider谱与JONSWAP谱作用下的随机液体晃荡现象．当有效波高和谱峰周期相同时，液舱在Bretschneider谱生成的不规则波激励下，会产生更为剧烈的波动现象．当有效波高保持不变时，自由液面高程的变化幅度随着谱峰周期的增加而减小；当谱峰周期保持不变时，自由液面高程变化的幅度随着有效波高的增大而增大．基于快速傅里叶变换，对自由液面高程时间历程的频域分析表明，自由液面波形的变化主要受液舱最低固有频率的调制．由液体晃荡生成的自由表面波的能量主要分布在液舱的最低固有频率附近，谱峰频率与谱型对晃荡波的能量在频率上的分布没有显著的影响．此外，通过试验观测发现在海浪谱作用下，液舱内容易生成破碎行进波．

相同波要素时，Bretschneider谱作用下，液舱右侧壁的最大动态压力大于JONSWAP谱作用下的最大动态压力，而且最大动态压力在液舱内壁上的分布，从液舱底部到自由液面依次增大，且位于自由液面上的压力测点处的最大动态压力一般大于自由液面下压力测点处的最大动态压力．当有效波高保持不变时，晃荡的液体对液舱右侧壁的冲击压力随着谱峰周期的增加而减小；当谱峰周期保持不变时，晃荡冲击压力随着有效波高的增加而增大．

[1] FALTINSEN O M, TIMOKHA A N.Sloshing[M]. Cambridge: Cambridge University Press, 2009.

[2] 张海涛,孙蓓蓓,陈建栋,等. 运动容器内液体大幅非线性晃动实验研究 [J]. 东南大学学报(自然科学版), 2017,47(1):33-37.

ZHANG Haitao, SUN Beibei, CHEN Jiandong,etal. Experimental study on large-amplitude nonlinear liquid sloshing in moving container [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2017,47(1):33-37. (in Chinese)

[3] 宁德志,宋伟华,滕 斌. 纵摇容器中液体晃荡的非线性数值模拟[J]. 船舶力学, 2017,21(1):15-22.

NING Dezhi, SONG Weihua, TENG Bin. Nonlinear numerical simulation of liquid sloshing in a container subjected to pitch excitation [J].JournalofShipMechanics, 2017,21(1):15-22. (in Chinese)

[4] 卫志军,陈晓东,董玉山,等. 两种运动平台下晃荡冲击荷载的实验研究[J]. 船舶力学, 2015,19(7):841-849.

WEI Zhijun, CHEN Xiaodong, DONG Yushan,etal. An experimental study of slamming impact load on two platforms [J].JournalofShipMechanics, 2015,19(7):841-849. (in Chinese)

[5] CHEN W, HAROUN M A, LIU F. Large amplitude liquid sloshing in seismically excited tanks [J].EarthquakeEngineering&StructuralDynamics, 1996,25(7):653-669.

[6] NASAR T, SANNASIRAJ S A, SUNDAR V. Wave-induced sloshing pressure in a liquid tank under irregular waves [J].ProceedingsoftheInstitutionofMechanicalEngineersPartM-JournalofEngineeringfortheMaritimeEnvironment, 2009,223(M2):145-161.

[7] 蒋梅荣,任 冰,李小超,等. 有限液深下弹性侧壁液舱内晃荡共振特性实验研究[J]. 大连理工大学学报, 2014,54(5):558-567.

JIANG Meirong, REN Bing, LI Xiaochao,etal. Experimental study of resonant behavior of sloshing in elastic bulkhead tanks under finite depth [J].JournalofDalianUniversityofTechnology, 2014,54(5):558-567. (in Chinese)

[8] 朱仁庆,马海潇,缪泉明,等. LNG船液舱晃荡压强预报[J]. 船舶力学, 2013,17(1/2):42-48.

ZHU Renqing, MA Haixiao, MIAO Quanming,etal. Prediction of pressure induced by liquid sloshing for LNG carrier [J].JournalofShipMechanics, 2013,17(1/2):42-48. (in Chinese)

[9] 李文刚,金玉姬,高 锐. 水平地震激励下储罐液体晃动分析[J]. 自然灾害学报, 2007,16(2):138-142.

LI Wengang, JIN Yuji, GAO Rui. Sloshing analysis of fluid in storage tank under lateral seismic excitation [J].JournalofNaturalDisasters, 2007,16(2):138-142. (in Chinese)

[10] ZAMA S, NISHI H, YAMADA M,etal. Damage of oil storage tanks caused by liquid sloshing in the 2003 Tokachi Oki earthquake and revision of design spectra in the long-period range [C] //The14thWorldConferenceonEarthquakeEngineering. Beijing: International Association for Earthquake Engineering, 2008.

[11] IKEDA T, IBRAHIM R A. Nonlinear random responses of a structure parametrically coupled with liquid sloshing in a cylindrical tank [J].JournalofSoundandVibration, 2005,284(1/2):75-102.

[12] WANG C Z, KHOO B C. Finite element analysis of two-dimensional nonlinear sloshing problems in random excitations [J].OceanEngineering, 2005,32(2):107-133.

[13] SRIRAM V, SANNASIRAJ S A, SUNDAR V. Numerical simulation of 2D sloshing waves due to horizontal and vertical random excitation [J].AppliedOceanResearch, 2006,28(1):19-32.

[14] CHEN B F, CHIANG H W. Complete two-dimensional analysis of sea-wave-induced fully non-linear sloshing fluid in a rigid floating tank [J].OceanEngineering, 2000,27(9):953-977.

[15] 邓 棋,尤云祥,张新曙. 超谐共振横摇下液舱晃荡特性数值研究[J]. 水动力学研究与进展(A辑), 2016,31(5):525-534.

DENG Qi, YOU Yunxiang, ZHANG Xinshu. Numerical study on tank sloshing characteristics under super-harmonic resonance rolling [J].ChineseJournalofHydrodynamics:A, 2016,31(5):525-534. (in Chinese)

[16] XUE Mi′an. Experimental study of liquid sloshing in a tank under irregular wave excitation [C] //34thIAHRWorldCongress-BalanceandUncertainty. Brisbane: International Association for Hydro-Environment Engineering and Research, 2011.

[17] XUE Mi′an, ZHENG Jinhai, LIN Pengzhi,etal. Experimental study on vertical baffles of different configurations in suppressing sloshing pressure [J].OceanEngineering, 2017,136:178-189.