基于自适应数学形态学的滚动轴承故障诊断方法

2018-05-30齐咏生，张双龙，高胜利，李永亭，王林

大连理工大学学报 2018年3期

齐咏生，张双龙，高胜利，李永亭，王林

( 1.内蒙古工业大学电力学院，内蒙古呼和浩特 010080；2.内蒙古北方龙源风力发电有限责任公司，内蒙古呼和浩特 010050 )

0 引言

滚动轴承是各种旋转机械的关键部件之一，其健康状况影响整个机械系统的运行．鉴于对滚动轴承可靠性和安全性的迫切需求，有必要对其故障的识别和诊断进行深入研究[1]．当滚动轴承外圈、内圈以及滚动体出现点蚀等故障时，处于运行状态的轴承就会产生一些特定频率的冲击，引起轴承的振动，而旋转轴承的非稳定性，使得振动信号呈现非线性、非平稳状态．此时，从中准确地提取故障特征信息就成为滚动轴承故障诊断的关键[2]．

目前，传统的非线性、非平稳信号处理的方法主要有短时傅里叶变换、小波变换、经验模态分解(EMD)等．短时傅里叶变换分析的效果主要由所选定的窗函数决定，窗函数最终确定分辨率，如果分辨率不满足要求，则需要重新选择窗函数，而且不同特征的信号必须选择相适应的窗函数，使得结果难以把握．小波变换经过几十年的发展目前已成为时频分析技术中最主要的方法之一，在滚动轴承故障特征提取中得到了普遍应用[2-3]，但是小波分析也有其局限性：首先，小波变换归根到底还是以傅里叶变换为基础的，受到不确定性原理的制约，不可能同时在时域和频域有无限高的分辨率；其次，不同信号要选择合适的小波基，而如何选择小波基仍是开放性的问题[4]．EMD是分析非平稳信号和非线性信号的有力工具，但是存在缺失严格的数学基础、算法效率低、模态混叠等问题．EEMD是在EMD基础上的改进算法[5]，该算法能有效抑制模态混叠现象，但依然存在算法效率低等问题．

针对上述一些常见方法的信号特征提取技术在滚动轴承故障诊断方面的应用效果欠佳等问题，近年来，一种有效的非线性信号处理方法——数学形态学，被快速而广泛地应用到了信号特征提取中[6]．数学形态学通过数学集合分析来进行信号处理，同以往的信号处理技术不同之处在于：数学形态学处理是通过构造一个特定的结构元素(structuring element，SE)来提取信号的有用信息，即运用结构元素在目标信号中从左至右移动，通过形态学基本算子进行比较，将一些噪声替换，保留下来该目标信号的绝大部分特征信息作为备用．因此，该方法具有很强的抑制脉冲干扰的能力，同时，形态学运算只包含膨胀和腐蚀两种基于加减法的运算算子，形态开和形态闭运算也只是以上两种算子的简单结合，与绝大部分在频域内处理方法相比运算速度更快、复杂度更小．

陈兆文[7]运用单独的开或闭运算实现了轴承信号的特征提取，使得计算速度更为快捷，效果显著；不过该算法中只针对信号的正或负脉冲进行处理，运用单一的开或闭运算，未考虑开闭运算的综合运用．一定程度上，可能造成滚动轴承振动信号中有用信息的损失．为了减小处理误差，使该方法有效滤除噪声的同时还能尽可能保持信号的完整性，Chen等[8-9]提出了多尺度形态学处理方法，该方法采用单一开运算对信号进行多尺度运算，获得滚动轴承信号中不同尺度的有用信息．不过，上述方法仍未考虑开闭算子的综合运用问题．

针对上述问题，本文提出一种自适应形态学方法，即将形态开和形态闭运算以更合理的比例进行分配，以有效提高信号的特征提取能力．然后结合谱相关分析法，根据待测未知信号与训练过信号的互相关系数大小来识别未知信号的故障类型和等级，以提高识别率．

1 基于自适应数学形态学的信号处理方法原理

1.1 数学形态学的基本理论

数学形态学的基本运算包括膨胀、腐蚀，以此为基础可以构成形态开和形态闭．设某故障信号为f(n)，定义域为Df={0，1，…，N}，定义g(n)为结构元素，域为Dg={0，1，…，P}，且P≤N，则f(n)关于g(n)形态腐蚀和膨胀运算公式如式(1)和(2)所示：

(f⊖g)(n)=min{f(n+x)-g(x)|(n+x)∈

Df，x∈Dg}

(1)

(f⊕g)(n)=max{f(n-x)+g(x)|(n-x)∈

Df，x∈Dg}

(2)

基于腐蚀和膨胀运算的简单组合，形态开和闭运算公式如式(3)和(4)所示：

f∘g=f⊖g⊕g

(3)

f·g=f⊕g⊖g

(4)

开、闭运算分别可以抑制信号中的峰值噪声和低谷噪声[10]．

1.2 基于自适应的三角结构元素

1.2.1 自适应的三角结构元素的构造在数学形态学分析中，结构元素是该算法的核心组成，它的作用类似一个特征提取“窗”，所选取的“窗”的几何特征与该“窗”所框住的信号越相似，该部分信号能提取的特征信息就越多．根据经验，在滚动轴承的故障诊断研究中，当滚动轴承出现局部缺陷时，其振动信号会产生富含该类故障信息的振动冲击，当轴承出现不同缺陷或者不同程度的缺陷时，所产生的振动冲击的特征也不同，因此对于不同的故障信号应选取不同的结构元素来分析．考虑到振动信号的非线性特点，该信号任意3个点所构成的几何形状类似一个三角形，再者以往学者运用三角结构元素处理振动信号也取得了一些成功[7]，因此本文采用三角结构元素来分析滚动轴承的故障特征．

选定结构元素的形状之后，三角结构元素的高可能是对特征信号提取影响重大的参数．考虑到形态学分析方法是处理时域内的信号，而不同故障信号的幅值呈现统计学分布，因此本文运用信号幅值的标准差σ来探究结构元素高度．

假设故障信号服从统计学的nσ(n=1，2，3)规律，那么认为信号的幅值绝对值在±nσ范围内的部分主要是由于轴承故障造成的，所包含的特征信息就是需要提取的轴承故障信息．根据统计学知识，由于±3σ所覆盖的信号幅值统计范围高达99.7%，即统计范围覆盖绝大部分特征信息，因此本文假定±3σ处所对应的信号幅值绝对值等于三角结构元素的高．此时，所得结构元素可能最有利于滚动轴承故障特征的提取．确定好结构元素的形状和高度之后，考虑到数学形态学中，结构元素宽度越小，则信号的细节保持得越好，信号的脉冲数也就提取得越多，因此本文结构元素选定为3．

本文三角结构元素具体构造过程如图1所示．

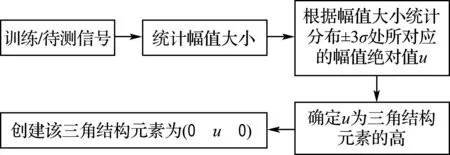
图1 自适应的三角结构元素的构造过程Fig.1 The construction process of adaptive triangular structuring elements

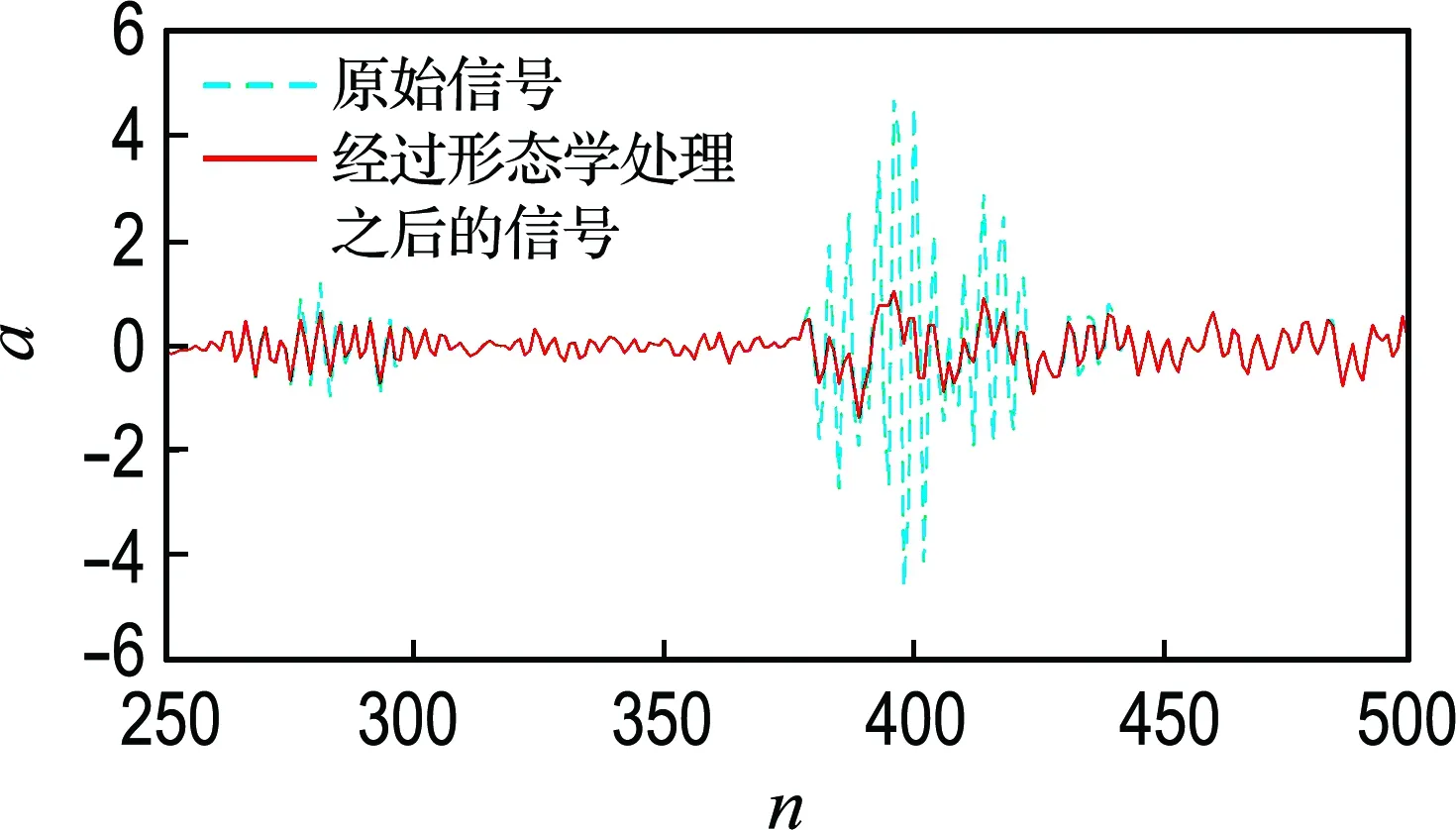
1.2.2 假定的验证为验证提出的假定，本文以美国西储大学(Case Western Reserve University，CWRU)数据中心转速为1 730 r/min、损伤直径为0.533 mm的滚动轴承外圈故障信号为例，以简单开闭运算为形态算子，分别采用±σ、±2σ、±3σ和大于±3σ处对应的信号幅值绝对值(0.14、0.61、2.67和10)作为三角结构元素的高，并将随之确定的结构元素应用到该信号的特征提取中，结果如图2所示．

图2(a)、2(b)表明提取特征信息过少使大量原始信号丢失；图2(d)表明信号处理前后几乎不发生变化，说明该结构元素失去特征提取的能力．而从图2(c)可知，信号经过形态学开闭运算之后既过滤了明显的噪声信号又尽可能多地保留了信号中的特征信息，该结构元素的特征提取能力明显优于其他取值，此外，采样其他案例也能获得相同的效果，表明本文确定三角结构元素高的方法是合理的．

1.3 自适应形态学方法

1.3.1 自适应形态学方法的提出形态学方法包含形态开和形态闭两个算子．本文提出一种自适应形态学方法，即以组合式形态学方式，增加一个自适应权重，使形态学方法在开闭运算上更具灵活性和适用性．该方法可表示如下：

(a) ±σ对应的幅值高度0.14

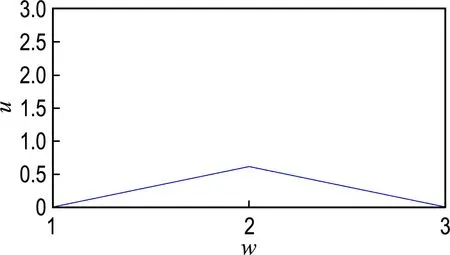
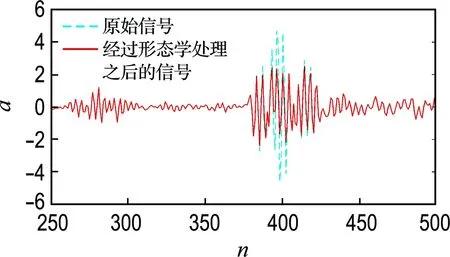
(b) ±2σ对应的幅值高度0.61

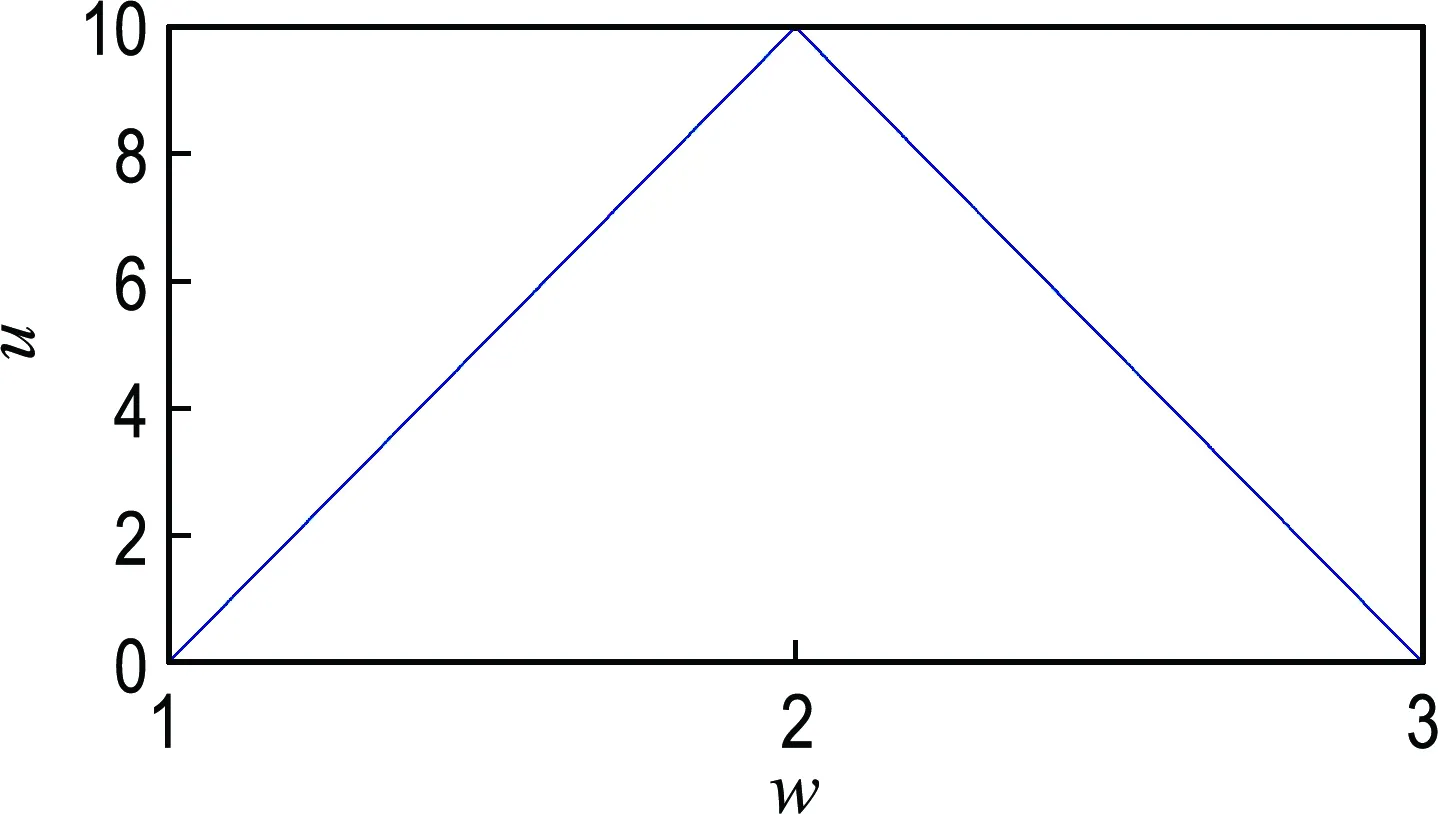
(d) 高度取10(大于±3σ对应的幅值高度)

图2 不同高度的三角结构元素的特征提取

Fig.2 Feature extraction of triangular structuring elements with different heights

y(n)=αFo(f(n))+(1-α)Fc(f(n))

(5)

式中：α为加权因子，0<α<1，y(n)为经过自适应形态学方法处理之后的信号，Fo、Fc分别表示对信号进行开和闭运算．适当调整权重，便可得到形态开闭和闭开运算后信号的权重，得到不同算子的滤波贡献，达到改善处理结果的目的．依据信号滤波评价——相关系数的比较选择更为恰当的加权因子α，即为本文提出的自适应形态学方法．

1.3.2 最优加权因子的选取α对自适应形态学方法的处理效果影响显著，需要谨慎选取．由式(5)可知，α取值较小，开运算处理后的信号在处理后的信号中的权重就较小，而闭运算处理后的信号权重就较大；反之亦然．为了均衡二者的权重比值，考虑到不同故障信号最适合的形态学算子也不同，本文以相关性系数评价指标为依据，选取达到最优信号滤波处理效果的α为最优权重．设定α取值范围为[αmin，αmax]，通常取αmin=0.1，αmax=0.9，则α的变换可采取步长递增法，即第k次权重变换的结果为

(6)

其中α0=0，Q为权重选取数量．

最优加权因子的选取过程如图3所示．

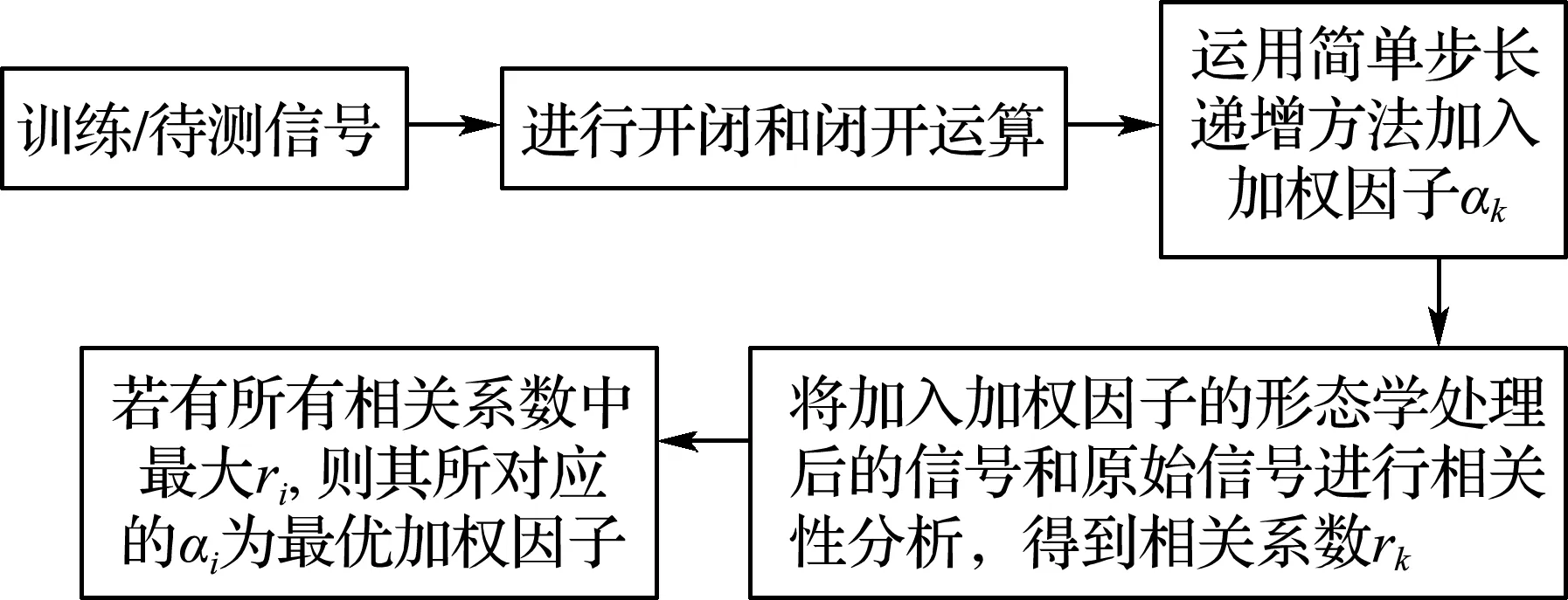
图3 最优加权因子的选取Fig.3 Selection of optimal weighting factors

2 基于自适应形态频谱相关分析的滚动轴承故障诊断方法

2.1 相关性分析

在滚动轴承故障诊断所有方法中，基于数学形态学的方法不失一般性地也能达到故障信号的识别和诊断，在具备一定先验条件的基础上可以结合信号频谱的相关性分析实现这一点．本文中，采用未知信号和已知故障信号进行相关性分析，相关系数的变化范围为-1～1，相关系数越趋近于1表明两组信号波形越相似．目前相关性分析在滚动轴承故障诊断方面的运用已经取得一些成功[11-12]．

2.2 滚动轴承故障诊断方法

图4为本文方法的流程示意图，方法包含两部分：左半部分为训练建模过程，对已知正常、内圈故障、外圈(包括3点钟方向、6点钟方向和12点钟方向)故障共6类数据的训练预处理；右半部分为方法应用过程，即对待测信号进行故障识别和诊断．

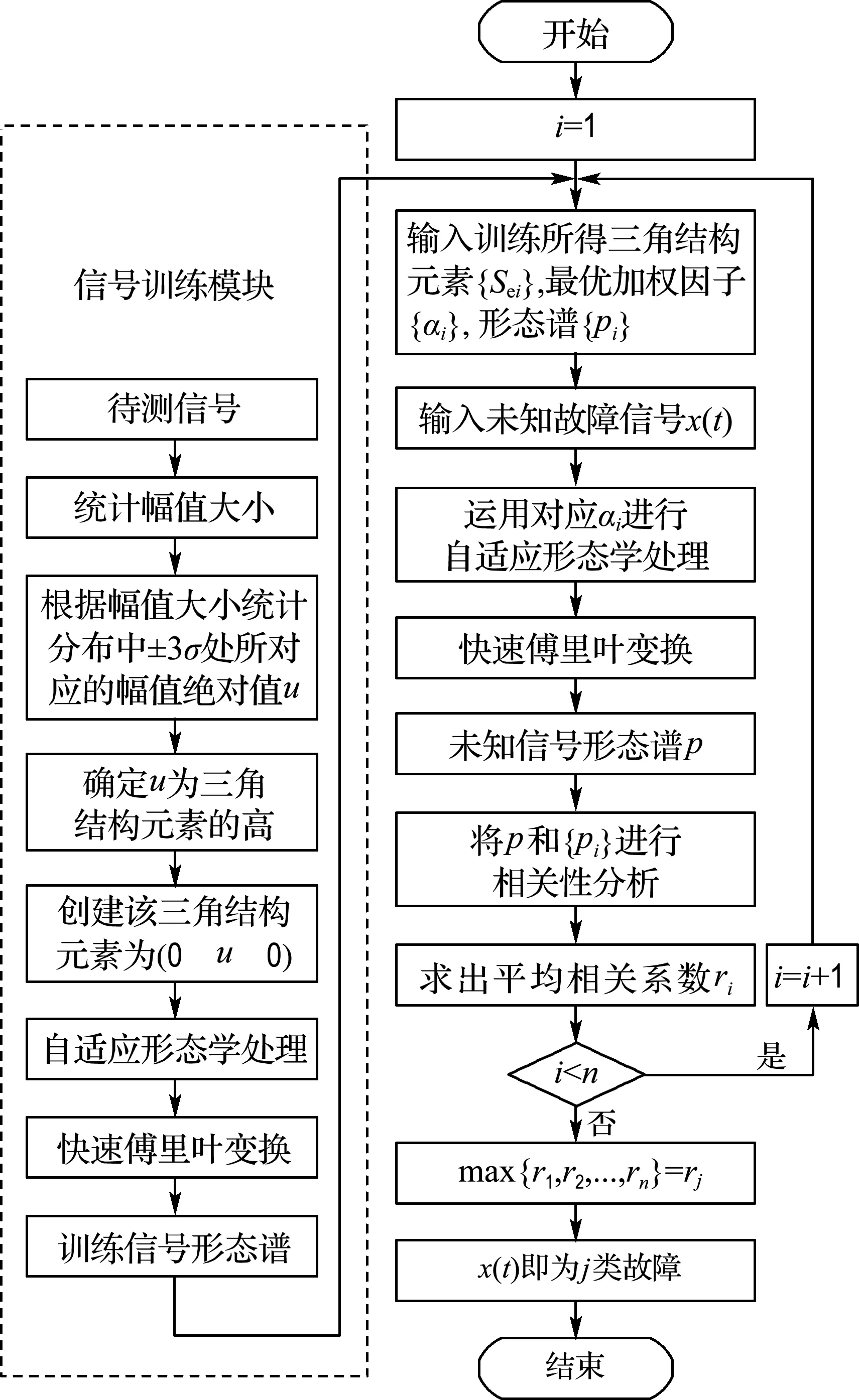
图4 基于自适应形态谱相关分析的轴承故障诊断方法

Fig.4 Fault diagnosis method of bearing based on adaptive morphological spectrum correlation analysis

该方法具体实施步骤如下：

(1)根据目前已知的轴承故障类型将训练信号分成m类，每一类包含n个训练样本信号．分别组成信号集合{xi，j}(i=1，2，…，m;j=1，2，…，n)．根据1.2节所述三角结构元素的构造方法计算出各类已知信号所对应的三角结构元素{Sei}(i=1，2，…，m)．

(2)根据1.3节所述方法确定相对应故障信号自适应加权因子{αi}(i=1，2，…，m)，采用自适应开闭运算和结构元素Sei对信号集合{xi}进行处理，以提取信号集合{xi}的特征信息．

(3)釆用快速傅里叶变换对处理后的信号集合{xi}(i=1，2，…，m)进行变换得到与之对应的自适应形态谱集{pi}(i=1，2，…，m)．

(4)对于未知故障状态的轴承信号x(t)，分别采用由训练预处理得到的三角结构元素{Sei}(i=1，2，…，m)和对应故障信号自适应加权因子{αi}(i=1，2，…，m)对其进行形态学处理以提取该信号的特征，进而通过傅里叶变换得到该信号的自适应形态谱p．分别计算待测信号的自适应形态谱p和训练预处理的自适应形态谱集{pi}之间的平均相关系数ri．假设r1到rm中最大的一个为rs(0

3 实验验证

3.1 轴承振动数据说明

为了验证本文所提出方法的有效性，本文采用美国西储大学轴承数据中心负载为2.21 kW、转速为1 730 r/m、采样频率为12 000 Hz的轴承驱动端振动信号进行了仿真验证．该数据对应的轴承健康状态包括正常、内圈故障、外圈故障以及滚动体故障4种类型，损伤直径用到了0.178和0.533 mm两类．其中轴承外圈故障数据又包括损伤位置3点钟方向(@3:00)、6点钟方向(@6:00)、12点钟方向(@12:00)的数据．

3.2 自适应形态学方法α取值比较

如图5所示，给出了自适应算法中α值确定曲线(纵坐标r为相关系数，横坐标k为权重变换数量，权重选取数量Q取18)，由图可知，r随着k变化，经过自适应形态学处理的信号与原始信号的相关性呈现先升高后降低的变化趋势，即存在最大值．由此可说明自适应形态学方法的提出相比单一形态学算子进行信号处理更具合理性，针对已知故障特征的信号求得最优加权因子，能提高相应结构元素的特征提取能力．

图5 自适应形态学方法α取值比较Fig.5 Comparison of α of adaptive morphological methods

3.3 自适应形态学方法和单一闭运算形态学方法在故障识别率方面的比较

为了验证本文提出的自适应形态学方法在故障识别提取方面的可靠性，这里将该方法与传统的单一闭运算形态学方法进行了比较．

采用西储大学损伤直径为0.533 mm的轴承故障数据进行仿真比较实验．验证信号选择外圈(@3:00) 故障信号．仿真结果如图6所示．分别使用自适应形态学方法和单一闭运算形态学方法对已知信号进行处理，这里选取相关系数对应提升最高的点为代表加入定量分析，那么识别结果的可靠性参考值为

(8)

式中：i表示实验选取的信号对数．下标ADP表示进行自适应形态学方法处理的实验结果，MM表示经过传统单一闭运算处理的实验结果．通过式(8)计算可得，该案例中识别结果的可靠性参考值为3.06%，自适应形态学方法相对传统的单一闭运算处理的相关系数更高，有利于提高识别率，提高结果的可靠性．

图6 自适应形态学和单一闭运算形态学处理比较Fig.6 Comparison of adaptive morphological processing and single closed processing

3.4 仿真结果分析比较

3.4.1 不同类型的故障识别仿真实例如表1所示，本文选用损伤直径为0.178和0.533 mm轴承分别进行实验．数据包A中共有90个训练样本和72个检验样本，每类轴承健康状况对应15个训练样本和12个检验样本，每个训练样本和检验样本都包含6 000个采样点．数据包B和数据包A类似，不同之处在于轴承损伤直径．

具体训练所得参数如表2、3所示．

表1 不同类型故障的实验数据

表2 损伤直径为0.178 mm的故障特征指标

表3 损伤直径为0.533 mm的故障特征指标

图7、8列出了损伤直径为0.178 mm的滚动体和0.533 mm的外圈(@6:00)故障类型的识别结果．由图可知，在同一损伤程度的不同故障类型模型中，数学形态学方法对故障的识别效果明显．此外，为了比较，图中将传统的单一闭运算数学形态学方法识别效果曲线也加入其中，通过式(8)计算可得，两种故障识别结果的可靠性参考值分别为9.26%和5.08%，自适应的数学形态学方法对故障的识别率有明显的提高．尤其从图7可以看出，自适应方法能有效降低实验干扰项对实验结果的影响．

图7 损伤直径为0.178 mm的滚动体故障诊断Fig.7 Ball fault diagnosis with damage diameter of 0.178 mm

图8 损伤直径为0.533 mm的外圈(@6:00)故障诊断Fig.8 Outer race (@6:00) fault diagnosis with damage diameter of 0.533 mm

3.4.2 不同损伤等级的故障识别仿真实例为进一步表明本算法的有效性，对轴承的不同程度损伤故障进行了仿真实验，表4为实验数据．

如图9、10所示，列出了损伤直径为0.355 mm的滚动体和外圈(@6:00)故障不同损伤程度下的诊断结果．由图可知，在同一故障类型的不同损伤程度识别模型中，通过式(8)计算可得，两种故障识别结果的可靠性参考值分别为10.99%和5.93%，自适应形态学方法能有效区分出不同损伤程度等级的故障，识别效果明显．

3.4.3 综合模型的故障识别实例综合上述各类故障及不同损伤程度的故障，进行综合相关性比较，如图11所示，进一步验证算法的有效性．

表4 不同损伤等级的故障数据

图9 损伤直径为0.355 mm的滚动体故障诊断Fig.9 Ball fault diagnosis with damage diameter of 0.355 mm

图10 损伤直径为0.355 mm的外圈(@6:00) 故障诊断Fig.10 Outer race (@6:00) fault diagnosis with damage diameter of 0.355 mm

如图11所示，所列为3种损伤等级下共14种损伤直径为0.533 mm的滚动体故障诊断结果．通过式(8)计算可得，该类故障识别结果的可靠性参考值为2.51%，由图可知，本文提出的自适应数学形态频谱相关分析方法能识别出不同故障类型，也能在相对复杂的情况下识别出损伤的等级并能提高结果的可靠性．

4 结语

数学形态学具有幅值不偏移和不衰减等诸多优点，本文提出一种改进的形态学方法诊断轴承故障．该方法在进行形态学的大量训练时能获得更多形态学所需的先验知识，为故障的识别和诊断提供更可靠的依据．结果通过该方法与谱相关分析相结合得到的相关系数得以体现．本文对不同故障类型同一损伤等级、同一故障类型不同损伤等级以及不同故障类型不同损伤等级进行了算法验证，结果表明该方法能明显提高结果的可靠性，具有一定的实用价值．

[1] HAMEED Z, HONG Y S, CHO Y M,etal. Condition monitoring and fault detection of wind turbines and related algorithms:A review [J].RenewableandSustainableEnergyReviews, 2009,13(1):1-39.

[2] LI Bing, ZHANG Peilin, MI Shuangshan,etal. An adaptive morphological gradient lifting wavelet for detecting bearing defects [J].MechanicalSystemsandSignalProcessing, 2012,29(9):415-427.

[3] OCAK H, LOPARO K A, DISCENZO F M. Online tracking of bearing wear using wavelet packet decomposition and probabilistic modeling:a method for bearing prognostics [J].JournalofSoundandVibration, 2007,302(4/5):951-961.

[4] 王大凯,彭进业. 小波分析及其在信号处理中的应用[M]. 北京:电子工业出版社, 2006．

WANG Dakai, PENG Jinye.WaveletAnalysisandItsApplicationinSignalProcessing[M]. Beijing:Electronic Industry Press, 2006. (in Chinese)

[5] LEI Yaguo, HE Zhengjia, ZI Yanyang. Application of the EEMD method to rotor fault diagnosis of rotating machinery [J].MechanicalSystemsandSignalProcessing, 2009,23(4):1327-1338.

[6] LI Bing, ZHANG Peilin, WANG Zhengjun,etal. Gear fault detection using multi-scale morphological filters [J].Measurement, 2011,44(10):2078-2089.

[7] 陈兆文. 基于信号的数学形态学方法及其在滚动轴承故障诊断中的研究应用[D]. 北京:北京化工大学, 2013.

CHEN Zhaowen. The signal based mathematical morphology analysis and its application in rolling element bearing fault diagnosis [D]. Beijing:Beijing University of Chemical Technology, 2013. (in Chinese)

[8] CHEN Qiong, CHEN Zhaowen, SUN Wei,etal. A new structuring element for multi-scale morphology analysis and its application in rolling element bearing fault diagnosis [J].JournalofVibrationandControl, 2015,21(4):765-789.

[9] CUI Lingli, GONG Xiangyang, ZHANG Yu. Research about rolling element bearing fault diagnosis based on mathematical morphology and sample entropy [C] //Proceedingsofthe20154thInternationalConferenceonSensors,MeasurementandIntelligentMaterials. Paris: Atlantis Press, 2016.

[10] 齐郑,李志,张首魁,等. 基于复合结构元素的新型自适应形态滤波器设计[J]. 电力系统保护与控制, 2017,45(14):121-127.

QI Zheng, LI Zhi, ZHANG Shoukui,etal. Design of a new adaptive morphological filter based on composite structure elements [J].PowerSystemProtectionandControl, 2017,45(14):121-127. (in Chinese)

[11] YOU Lei, HU Jun, FANG Fang,etal. Fault diagnosis system of rotating machinery vibration signal [J].ProcediaEngineering, 2011,15(1):671-675.

[12] SUN Wei, YANG Guoan, CHEN Qiong,etal. Fault diagnosis of rolling bearing based on wavelet transform and envelope spectrum correlation [J].JournalofVibrationandControl, 2013,19(6):924-941.