用于脉冲功率调制电路的电爆炸丝研究

沈 杰， 何 勇， 潘绪超， 陈 鸿， 贲 驰

(南京理工大学 智能弹药技术国防重点学科实验室， 南京 210094)

电磁脉冲弹药环境的特殊性对脉冲调制系统提出了可靠性高、体积小、质量小和抗过载能力强等要求。电感储能型脉冲调制采用磁场储能方式，储能密度高，适于调制系统的小型化和轻量化。电爆炸丝断路开关广泛应用于电感储能型脉冲调制系统中，具有结构简单、体积小和质量小等特点[1]。

林其文教授对电爆炸丝与传输线组合的脉冲功率调制系统进行了理论建模研究，讨论了电爆炸丝参数对脉冲调制性能的影响[2]。朱翼超等对电爆炸丝进行了仿真计算与实验研究，提出用电阻率-比作用量关系描述电爆炸丝特性，该方法具有合理性，为电爆炸丝的仿真和实验研究提供了重要参考[3-5]。在电爆炸实验研究的基础上，杨汉武建立了完整的电路仿真模型[6]，以读取图表的方法将复杂的电阻率-比作用量关系融入仿真模型中，对电爆炸丝进行了细致地仿真研究。赵科义对应用于高功率脉冲发生器中的电爆炸导体的特征参数进行了计算研究[7]。钟建忠对电爆炸丝电爆炸过程中产生的电磁脉冲辐射进行了研究，建立了电爆炸丝实验方案和电磁脉冲辐射信号测试方法[8]。

本文在已有研究基础上，进一步添加调制系统的能量守恒控制条件，以解决因仿真建模过程中引入大量功能性元件而导致的调制电路工作时打破能量守恒边界限制的问题。仿真模型中的功能性元件用于模拟电爆炸丝电阻值的迅速变化过程，却忽略了能量损耗，最终会导致系统输出的总能量远超系统输入的总能量，不符合能量守恒条件。本文在数学建模过程中，利用函数拟合电阻率与比作用量的特性关系曲线，相较常用的读取有限数据点后插值计算的仿真方式，进一步提高了仿真精度，可避免因跳过关键实验数据点而引起的仿真结果与实验结果不符的问题。

本文在Tucker等对多种金属导体材料的实验研究基础上[9-10]，对电爆炸丝的作用原理进行了数学建模和电路仿真；并通过电爆炸实验检验了仿真模型的合理性。最后结合电感储能脉冲功率调制电路进行了多变量仿真计算，探究了电爆炸丝长度、根数和充电电压对电压脉冲调制结果的影响规律。

1 电爆炸丝的工作原理

在电感储能脉冲功率调制中，电爆炸丝主要起迅速切断电路的作用。电爆炸丝工作时的电阻率变化过程如图1所示[11]。首先，当大电流流过电爆炸断路开关时，能量在电爆炸丝上以热能形式迅速积累，电爆炸丝随之升温；电爆炸丝先经历了固态熔化为液态、液态汽化为气态的物理变化过程，电阻率不断增大；随后电爆炸丝部分汽化分子和临近空气分子电离，共同形成了等离子体并迅速膨胀，电爆炸丝电阻率陡然增大，形成电爆炸切断现象，使电路断开，回路电流陡然下降[12]。最后，在电弧和金属等离子体的作用下，闭合调制系统回路，此时电爆炸丝的电阻率迅速下降[13]。

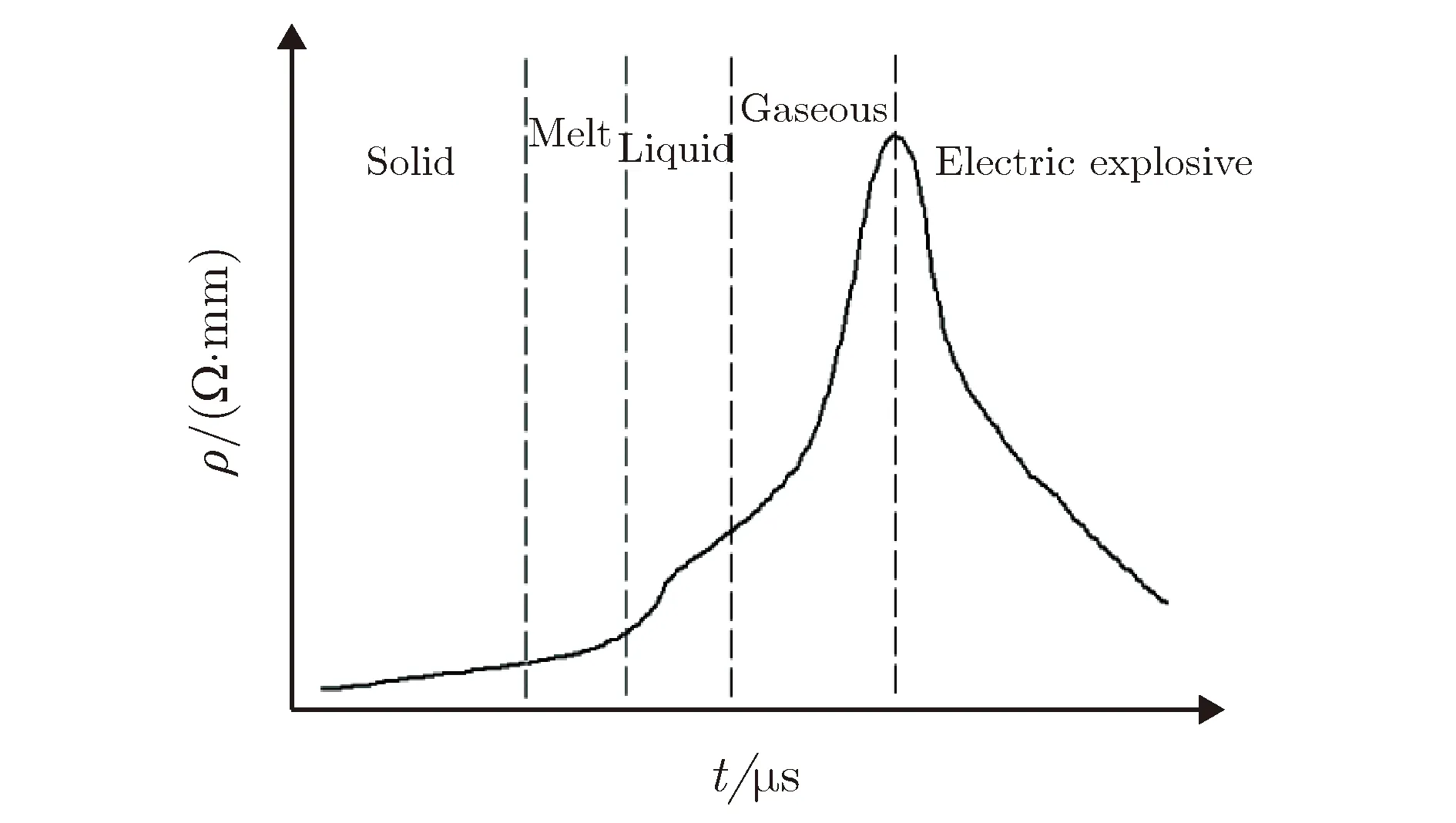
图1 电爆炸丝工作时的电阻率变化过程Fig.1 Electrical resistivity of electric exploding wire vs. time

金属丝的电爆炸切断过程十分迅速，可引起调制回路中的电感储能元件两端瞬间产生脉冲高电压，进一步加载到负载两端，实现提高输出脉冲峰值电压的效果。其实质是电感元器件存储的能量得到迅速释放，在总能量一定的情况下，以缩短能量释放时间的方式提高系统的输出功率。

2 电爆炸丝的数值仿真模型

2.1 电爆炸丝的数学模型

在一定的电流密度下，电爆炸丝的电阻率ρ可以表示为比作用量g(t)的函数，两者之间的关系如图2所示。比作用量g(t)是回路电流在电爆炸丝上随时间的累积，计算公式为

(1)

式中,j为流过电爆炸丝的电流密度，即电爆炸丝单位面积上流过的电流。

在常用的仿真模型中，一般读取ρ(g)-t曲线上的有限多个关键点数据后，以形成数据表格的方式参与到模型的计算过程中，并结合插值计算方法共同描述电爆炸丝的电阻率与比作用量之间的特征关系。此类建模方式，在多次循环计算后可能造成较大累积误差。

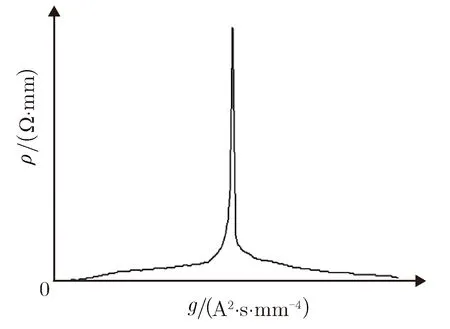
图2 电阻率与比作用量的关系曲线Fig.2 Relation curve between ρ and g

本文利用函数拟合电阻率与比作用量的特性关系曲线，将电爆炸丝的电阻率与比作用量的关系以分段函数的形式表示：

(2)

式中，ρ0为电爆炸丝的初始电阻率；ge1为电爆炸丝汽化点对应的比作用量；α、β和γ均为拟合系数，无量纲。Tucker等对23种金属材料进行了实验研究[9-10]，得到了材料在各物理状态转化点的电阻率ρ与比作用量g的实验数值，如表1所列。比作用量单位均为105A2·s·mm-4，电阻率单位均为10-5Ω·mm。

综合考虑材料电爆炸丝电阻率变化和经济性等因素，选择铜作为电爆炸丝材料。利用本文的函数模型和Tucker等得到的实验数据，可以确定式(2)中的各参数大小：ρ0=1.77×10-5Ω·mm，ge1=1.240×105A2·s·mm-4，α=13.859，β=1.307，γ=14.724。

将使用ρ(g)分段函数拟合的电阻率与比作用量的特性关系曲线，与使用Tucker等的实验数据点直接进行插值计算得到的电阻率与比作用量关系曲线进行对比，如图3所示。

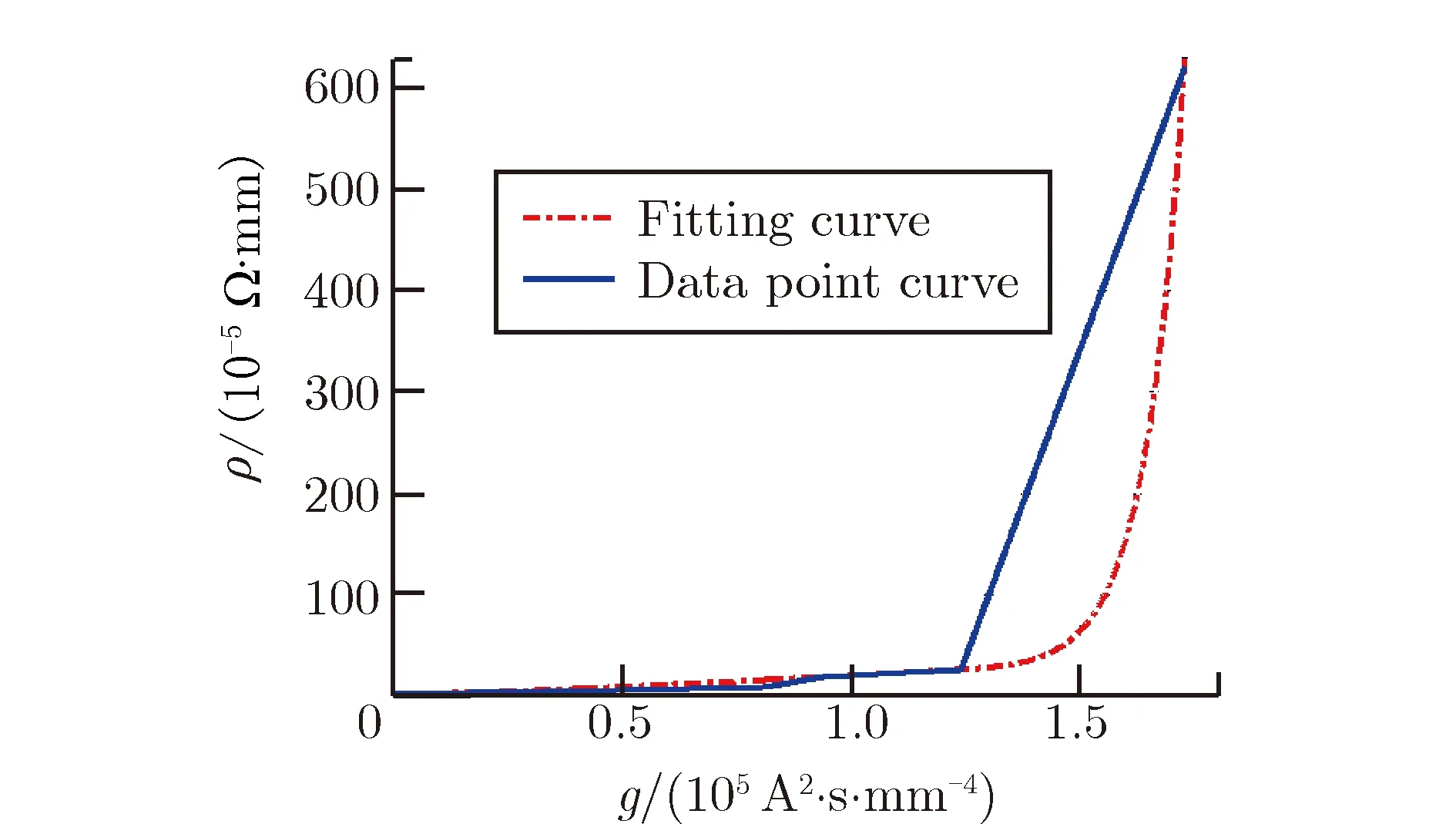
图3 函数曲线与数据点曲线对比Fig.3 Comparison between function curve and data point curve

在工作中电爆炸丝的电阻值REEOS不断变化，电爆炸丝所消耗的能量WEEOS应低于系统输入的总能量W0：

(3)

在仿真建模中，需要收集调制回路中的实时电流信号或电压信号进行运算处理，该功能的实现需要在模型中引入流控电压源、压控电压源以及函数运算等模块，会出现打破系统能量守恒边界限制的问题。本文在仿真模型中引入能量守恒控制条件，是对电爆炸丝仿真模型的进一步完善。

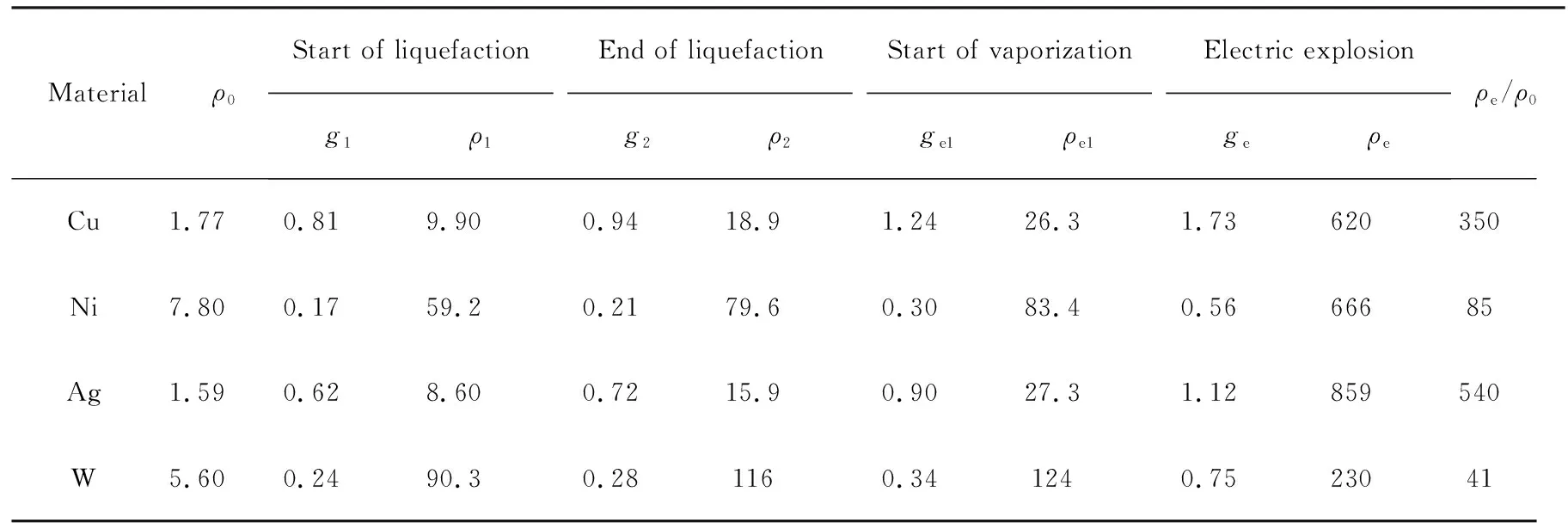
表1 部分常用材料的实验数据Tab.1 Experimental data of several commonly used materials

Note: unit ofg1,g2,ge1,ge: 105A2·s·mm-4unit ofρ0,ρ1,ρ2,ρe1,ρe: 10-5Ω·mm。

2.2 电爆炸丝的PSpice模型

PSpice电路仿真软件优点突出、功能完善，具有十分友好的用户界面，得到了国际公认。

根据电爆炸丝的工作原理，建立电爆炸丝仿真模型的流程框图如图4所示。首先获取流过电爆炸丝的实时电流信号I，对I进行平方计算和对时间t的积分运算，得到比作用量g；然后将g代入已建立的数学模型中，计算得到某时刻电爆炸丝的电阻率ρ；再根据所选的电爆炸丝参数，计算得到此时刻的电阻值REEOS；将实时电阻值REEOS与实时电流信号I做乘积运算，得到电爆炸丝两端的实时电压U，同时考虑能量守恒方程的约束，并将电压信号回馈到整体电路中；不断循环以上流程步骤，实现电爆炸丝的电路仿真计算。

根据图4，建立电爆炸丝的PSpice电路仿真模型如图5所示。因为PSpice仿真软件中对电压信号的处理能力较强，一般将电流信号转换为电压信号后再进行信号处理。本文所建立的仿真模型，应用电流控制电压源完成该项功能转换。仿真模型中的in1与in2为电爆炸丝的两端，电流由In1端流入，从In2端流出；AERFA为系数α，BETE为系数β，JAMA为系数γ；num为电爆炸丝的根数，r为单根电爆炸丝的半径，len为单根电爆炸丝的长度，mm。仿真模型中采用的积分步长为10 ns；ρ0=1.77×10-5Ω·mm；ge1=1.240×105A2·s·mm-4；α=13.859，β=1.307；γ=14.724。

3 电爆炸实验验证

电爆炸实验电路如图6所示，使用泰克P6015A型1 000倍高压探头和3 000∶1内置积分电路罗氏线圈分别测量电爆炸丝两端的电压与流经的电流。

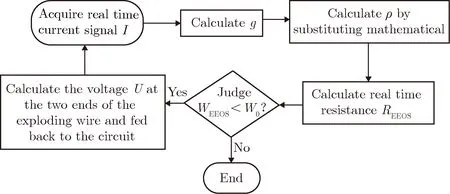
图4 电爆炸丝仿真模型的流程框图Fig.4 Simulation model of electric exploding wire

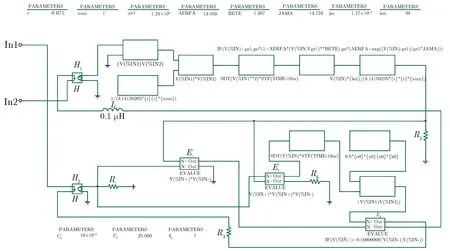
图5 电爆炸丝的PSpice仿真模型Fig.5 PSpice simulation model of electric exploding wire

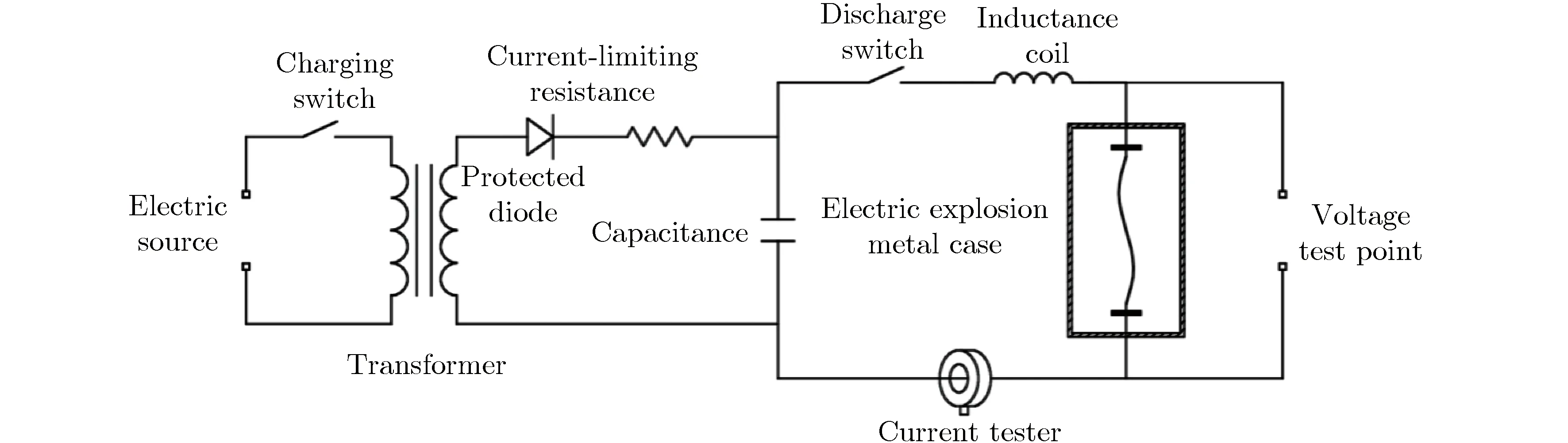
图6 电爆炸实验电路Fig.6 Experiment circuit of electric explosion

因电爆炸丝在电爆炸过程中会产生等离子体飞散和电磁脉冲辐射现象，可能损坏周围电子元器件及测试仪器，使用金属材质的电爆炸箱作为电爆炸防护措施。

电爆炸丝与实验回路的连接方式采用金属片机械夹持的方法，不采用普通焊接的方法，以避免因实验过程中焊点提前熔化脱落而导致实验回路接触不良或断开的问题。但电爆炸丝在端部夹持处易产生材料损伤，导致端部提前发生电爆炸现象，致使多次实验电爆炸一致性较差。实验过程中，采用在电爆炸丝两端并联直径相同、长度约5 mm电爆炸丝的方法，提高电爆炸丝的电爆炸稳定性。

先后进行了两轮实验，实验参数为：电爆炸丝直径φ为0.15 mm，长度l为80 mm，根数为1根，初始电阻R0为0.080 5 Ω；充电电容C为10 μF，充电电压U0为5 kV，中间储能电感L为10 μH。去除明显异常的测试数据后，得到5组可信实验数据。

因前后两轮实验使用的电爆炸丝批次不同，两次实验结果稍有差异。实验数据得到的平均电爆炸时刻te1=15.5 μs，平均电爆炸电压Ue1=24.2 kV；平均电爆炸时刻te2=15.3 μs，平均电爆炸电压Ue2=22.2 kV。PSpice仿真得到的电爆炸时刻te3=13.1 μs，爆炸电压Ue3=19.8 kV。实验测得电爆炸丝两端的电压曲线和PSpice仿真计算结果的对比，如图7所示。实验与理论仿真存在差异的主要原因在于：实验过程中在电爆炸丝的两端并联了一小段电爆炸丝，这就使直径φ为 0.15 mm的电爆炸丝的实际长度小于80 mm，因而导致电爆炸电压相对提高；放电开关为机械开关，闭合过程中存在打火现象，导致初期放电电流不稳定，电爆炸时刻相对延后；电爆炸丝电爆炸不完全，即存在局部材料电爆炸后在电弧和金属等离子体作用下迅速闭合回路，导致电压曲线提前下降，实验测得电压脉宽明显较小。虽然实验与理论仿真存在差异，但结果已十分相近，定性验证了PSpice仿真模型的合理性。

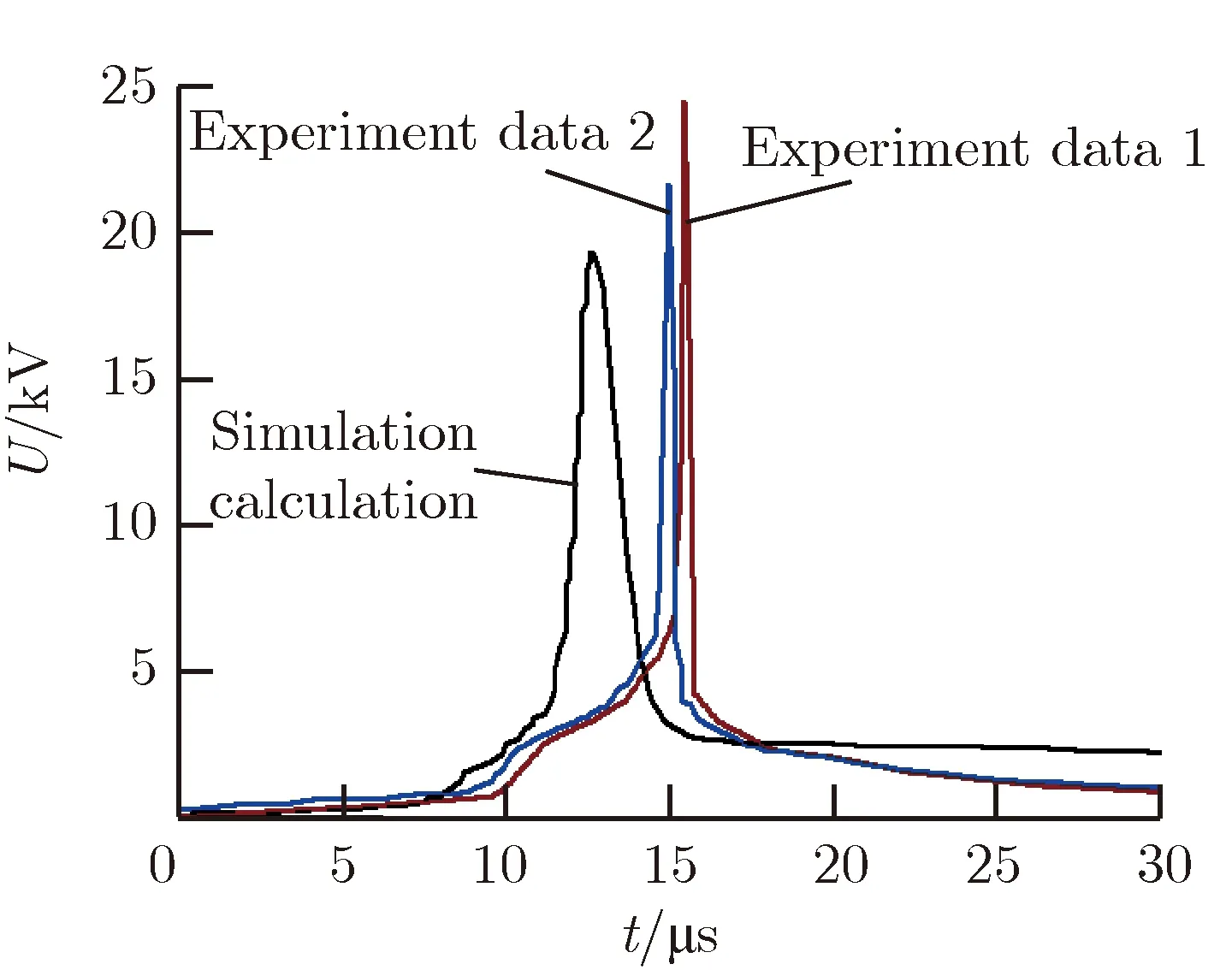
图7 电爆炸实验与仿真结果对比Fig.7 Comparison of experimental resultand simulation result

4 参数选择对电爆炸的影响

为了解电爆炸丝断路开关的电爆炸规律，需要改变电爆炸丝根数n、直径φ、长度l和充电电压U0等参数进行实验。在建立合理的电爆炸仿真模型后，通过仿真模拟计算，在一定程度上预测各参数对电爆炸的影响规律，以更好地解释实验现象。

1) 选择不同横截面积的电爆炸丝进行PSpice仿真研究。电爆炸丝根数n和直径φ的变化，实质上影响的是回路电流经过的横截面积大小。因此取电爆炸丝直径φ=0.15 mm，长度l=80 mm，充电电容C=10 μF，充电电压U0=30 kV，中间储能电感L=10 μH，仅改变电爆炸丝的根数n进行仿真计算，仿真结果如图8所示。

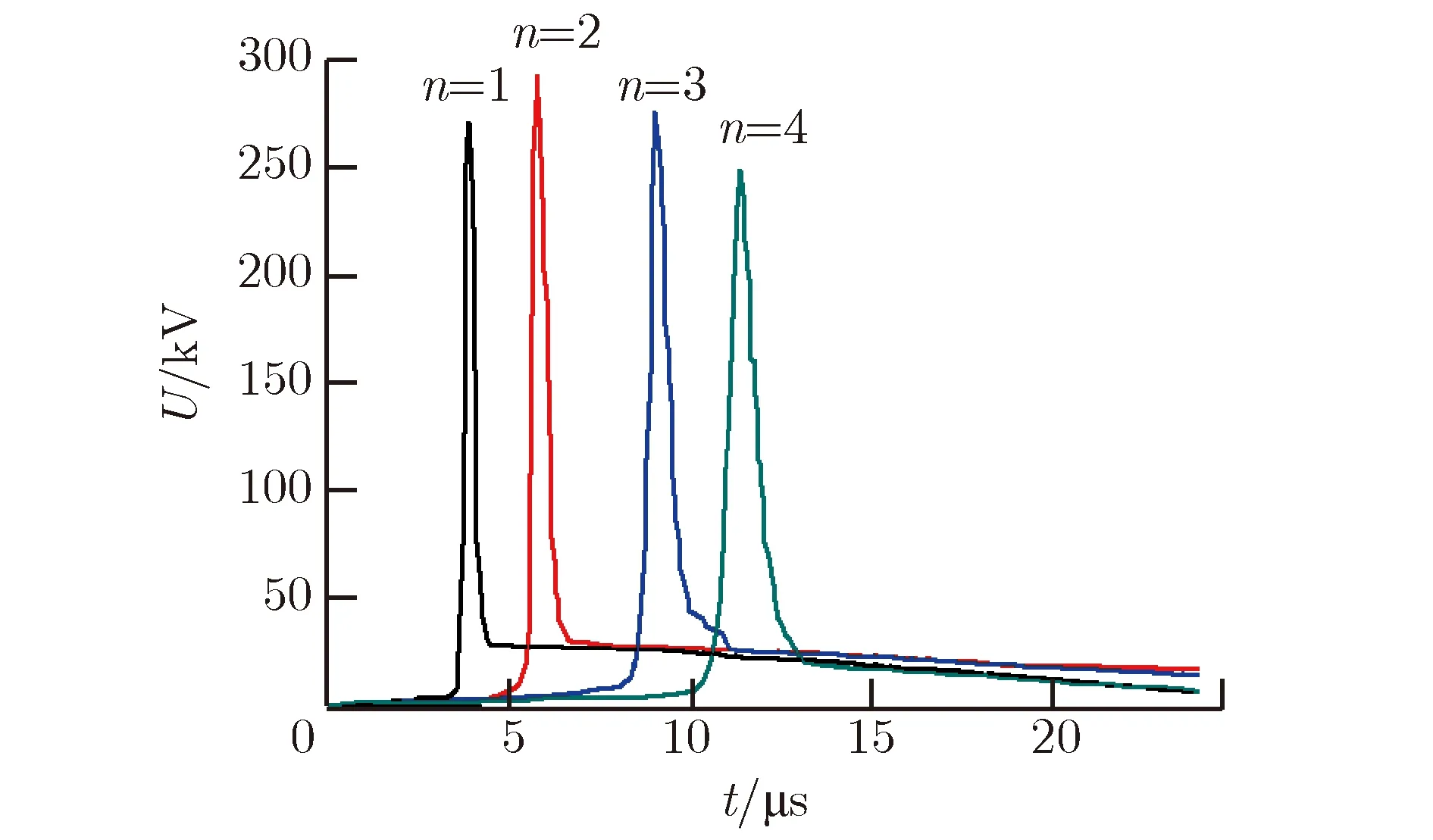
图8 电爆炸丝根数对电压脉冲调制结果的影响Fig.8 Influence of quantity of electric explosive wires on voltage pulse modulation results

电爆炸丝的电爆炸时刻te随着根数的增大而不断推迟。这是由于并联多根电爆炸丝或增大了电爆炸丝直径，造成了能量的分散而引起电爆炸时刻的推迟。

2) 选择不同长度的电爆炸丝进行PSpice仿真研究。取电爆炸丝直径φ=0.15 mm，根数n= 1，充电电容C=10 μF，充电电压U0=30 kV，中间储能电感L=10 μH，仅改变电爆炸丝的长度l进行仿真计算，仿真结果如图9所示。

电爆炸丝的电爆炸峰值电压Ue随着电爆炸丝长度l的增加而不断减小。当电爆炸丝长度过长时，甚至会导致电爆炸丝无法切断。长电爆炸丝可等效为多根短电爆炸丝的串联体，即单位长度上的电势差会随长度的增加而减小，当电势差小到一定程度时，必然导致电爆炸丝无法切断。

3) 选择不同充电电压U0进行电爆炸丝的仿真研究。取电爆炸丝直径φ为0.15 mm，根数n为1，长度l为80 mm，充电电容C为10 μF，中间储能电感L为10 μH，仅改变充电电压U0的大小进行仿真计算，仿真结果如图10所示。

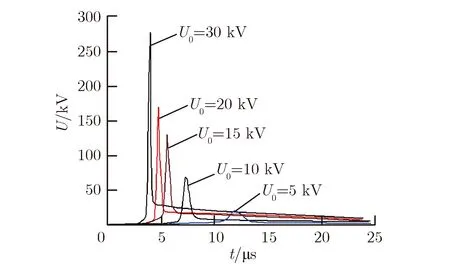
图10 不同充电电压对电压脉冲调制结果的影响Fig.10 Influence of charging voltage on voltage pulse modulation results

电爆炸丝的切断时刻te随着充电电压U0的增大而不断提前，电爆炸电压峰值Ue也随着充电电压U0的增大而不断提高。充电电压的增大使得电爆炸丝的能量积累过程更加迅速，使其更快达到电爆炸临界点。反之，若充电电压U0过小，电爆炸丝将无法产生电爆炸切断现象。当充电电压U0=1 kV时，电爆炸丝无法切断，电爆炸丝可等效为电阻，与调制回路中的电容和电感一同形成RCL振荡，仿真结果如图11所示。

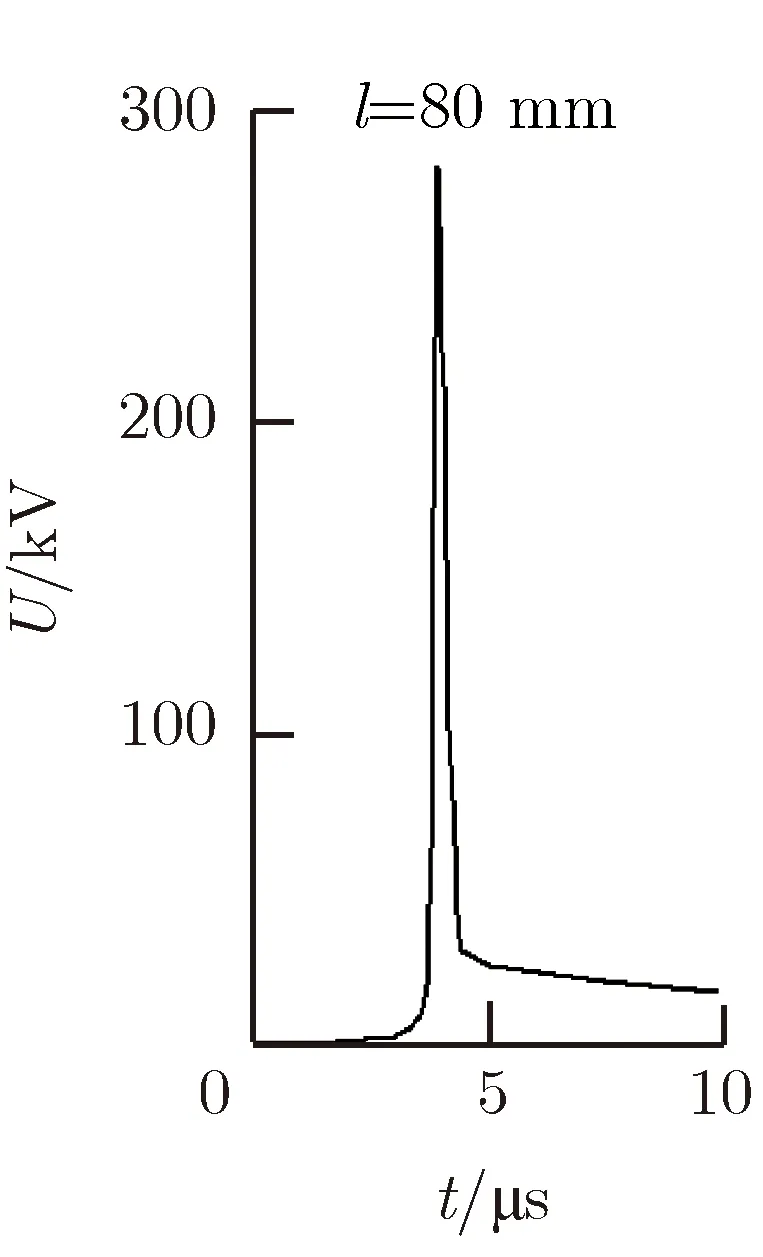
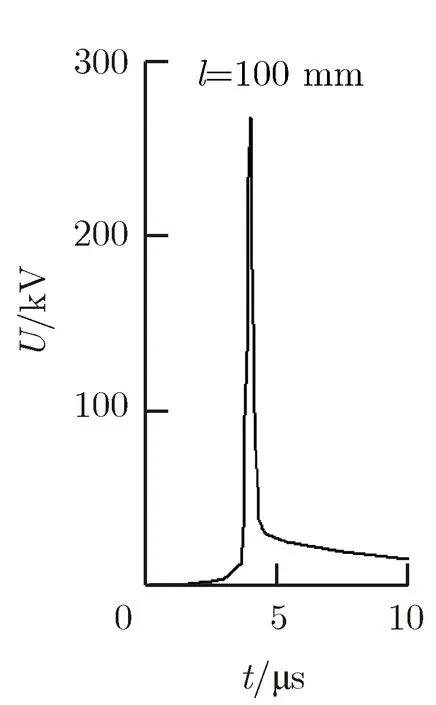
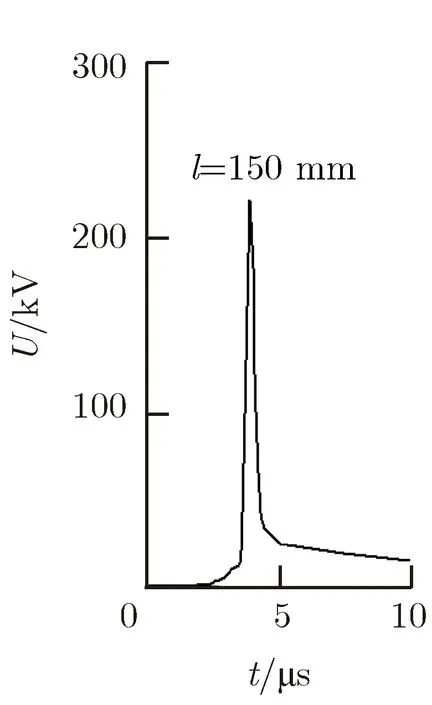
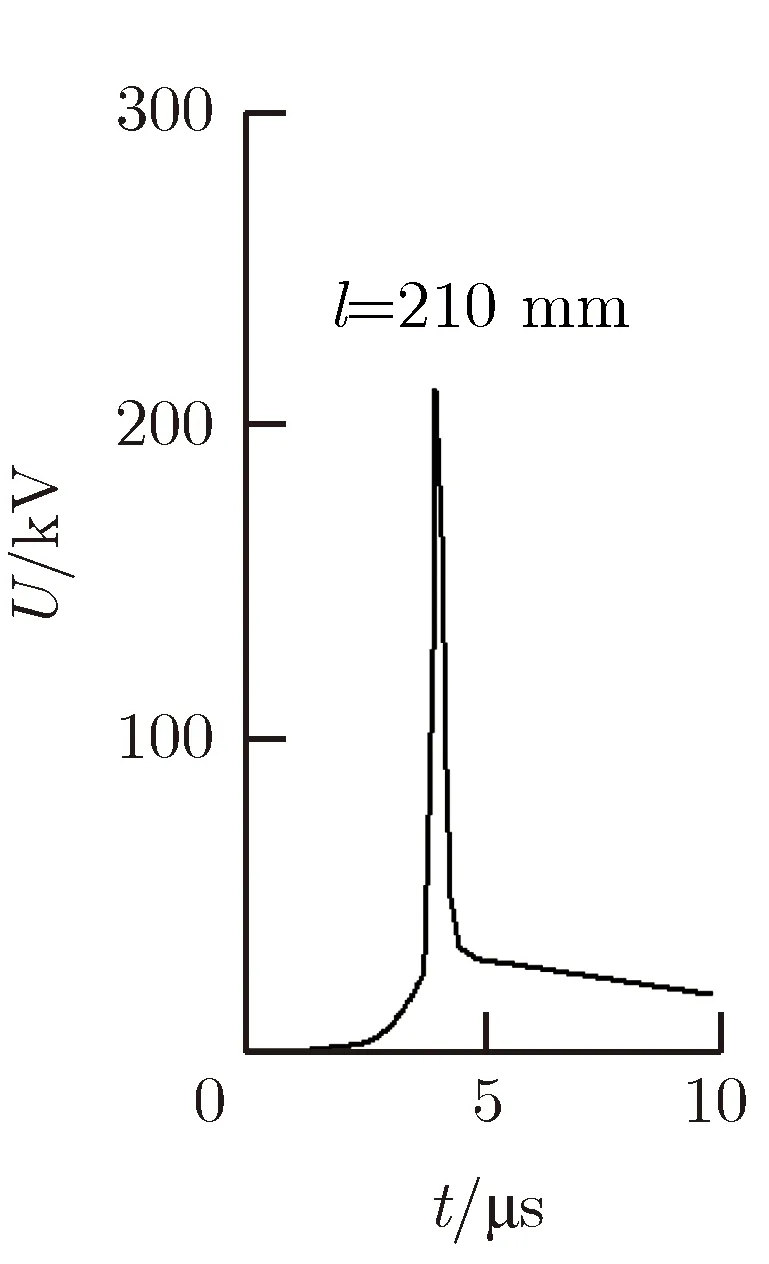
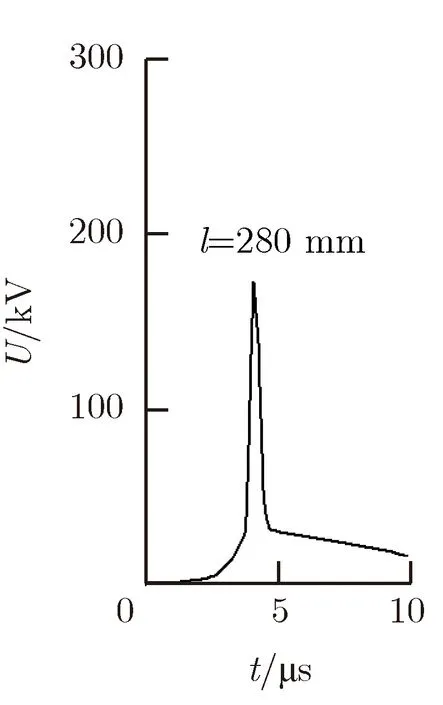
图9 电爆炸丝不同长度对电压脉冲调制结果的影响Fig.9 Influence of length of electric explosive wires on voltage pulse modulation results

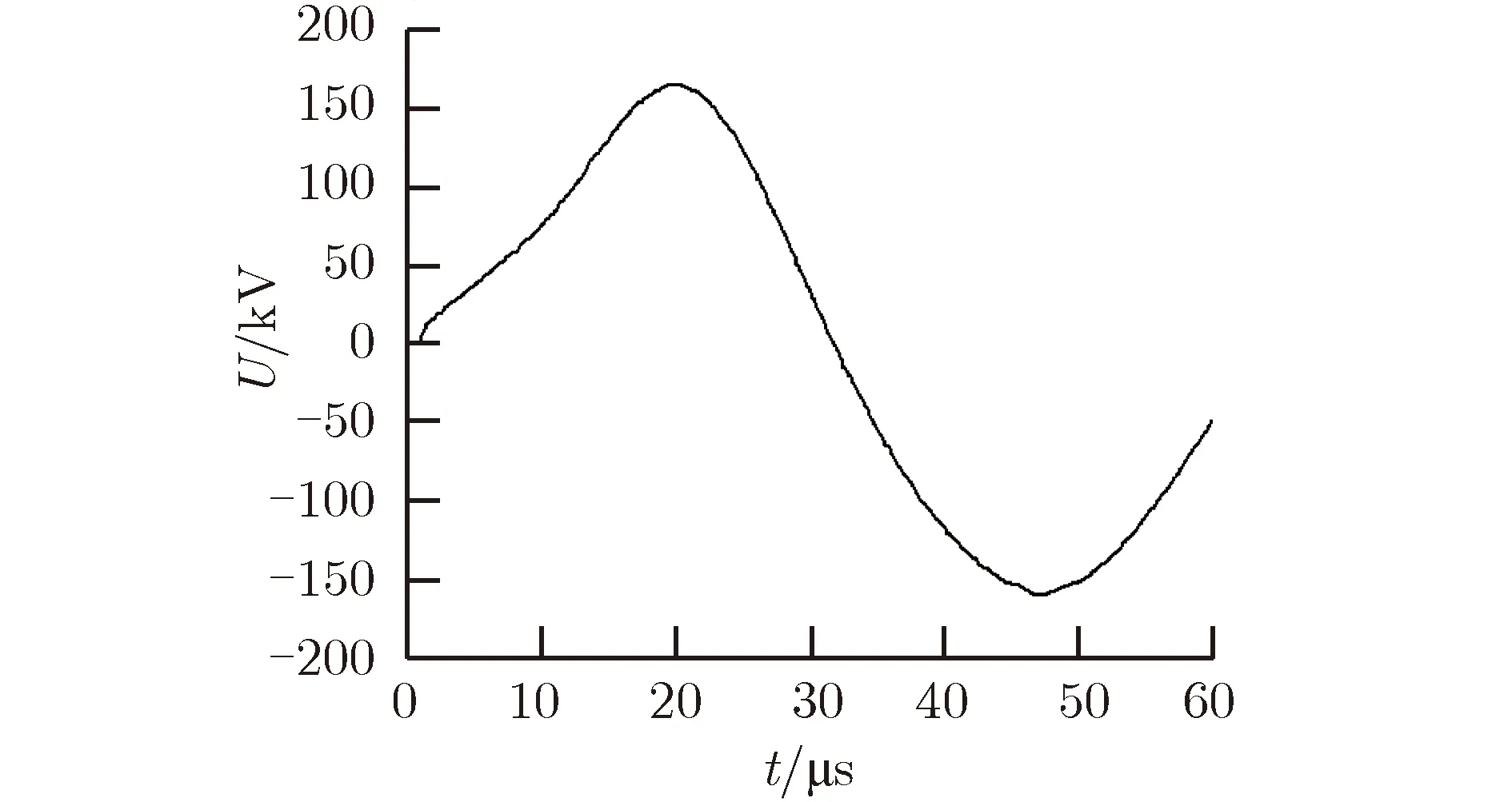
图11 充电电压为1 kV时的仿真结果Fig.11 Simulation results with 1 kV charging voltage

5 结论

本文对电爆炸丝的电阻率随比作用量的变化曲线进行了数学建模，使用特性曲线代替读取有限数据点表格的方式，完善了电爆炸丝的仿真模型；在仿真模型中增设了能量守恒控制条件，提高了电爆炸丝仿真模型计算的准确性。通过电爆炸实验与仿真结果的对比，定性验证了电爆炸丝仿真模型的合理性；最后结合电感储能脉冲功率调制电路，进行了多变量仿真计算，探究电爆炸丝长度、根数、横截面积和充电电压对脉冲调制结果的影响，得到以下规律：

1) 随着电爆炸丝根数、直径的增大，电爆炸时刻将不断推迟；

2) 随着电爆炸丝长度的增加，电路中di/dt不断减小，即电爆炸峰值电压不断减小；当电爆炸丝长度过长时，甚至会导致电爆炸丝无法正常切断。

3) 随着充电电压的增大，电爆炸切断时刻不断提前，电爆炸峰值电压不断增大。

本方法适用于电感储能脉冲调制系统的电爆炸调制的模拟仿真,可为实验研究提供借鉴和参考。

[1]杨家志， 蒋存波， 范兴明， 等． 电爆炸丝断路开关开断时间的实验研究[J]．高电压技术， 2015， 41(6)： 3 117-3 122. (YANG Jia-zhi, JIANG Cun-bo, FAN Xing-ming, et al. Switching time of electro-exploding wire opening switches [J]. High Voltage Engineering, 2015, 41(6): ： 3 117-3 122.)

[2]林其文， 高顺受． 电爆炸丝开关-传输线储能功率系统性能分析[J]． 强激光与粒子束， 1997， 9(2)： 283-288． (LIN Qi-wen, GAO Shun-shou. Analyses of performance for an electrical exploding opening switch-transmission line energy store power system [J]. High Power Laser and Particle Beams, 1997, 9(2): 283-288．)

[3]杨家志， 刘钟阳， 许东卫， 等． 电爆炸过程中金属丝阻抗的变化 [J]． 爆炸与冲击， 2009， 29(2): 205-208． (YANG Jia-zhi, LIU Zhong-yang, XU Dong-wei, et al. Wire resistance variation during its electrical explosion[J]. Explosion and Shock Wave, 2009, 29(2): 205-208.)

[4]朱翼超, 罗根新, 方向, 等. 电爆炸丝的电气特性 [J]. 爆炸与冲击, 2011, 31(6): 664-669. (ZHU Yi-chao, LUO Gen-xin, FANG Xiang, et al. Electrical characteristics of an electric exploding metal wire [J]. Explosion and Shock Wave, 2011, 31(6): 664-669.)

[5]朱翼超， 陈宇， 高成， 等． 组合开关高功率脉冲调制电路的研究[J] ． 电波科学学报， 2012， 27(3): 587-592．(ZHU Yi-chao, CHEN Yu, GAO Chen, et al. High-power and combined pulse modulation circuit [J]. Chinese Journal of Radio Science, 2012, 27(3): 587-592.)

[6]杨汉武， 钟辉煌． PSpice模型用于电爆炸丝的数值模拟 [J]． 国防科技大学学报， 2000， 22(增刊): 38-42． (YANG Han-wu, ZHONG Hui-huang. Numerical simulation of electric exploding wires via PSpice models[J]. Journal of National University of Defense Technology, 2000, 22(Suppl.): 38-42.)

[7]赵科义， 李治源， 吕庆敖， 等． 电爆炸金属导体在 Marx发生器中的应用 [J]．高电压技术， 2003， 29(10)： 47． (ZHAO Ke-yi, LI Zhi-yuan, LYU Qing-ao, et al. Application of electric exploding wire in wave’s reshaping of Marx generator[J]. High Voltage Engineering, 2003, 29(10): 47.)

[8]钟建忠， 刘列， 李立民， 等． 电爆炸丝断路开关的电磁辐射研究[J]． 高电压技术， 2007， 33(12)： 59-62．(ZHONG Jian-zhong, LIU Lie, LI Li-min, et al. Investigation of electromagnetic radiation generated from electric exploding opening switch[J]. High Voltage Engineering, 2007, 33(12) ： 59-62.)

[9]TUCKER T J, TOTH R P. EBW1: A computer code for the prediction of the behavior of electrical circuits containing exploding wire elements [A]. SAND-75-0041, Sandia National Labs, 1975.

[10] TUCKER T J, STANTON P L. Electrical gurney energy: New concept in modeling of energy transfer from electrically exploded conductors [R]. SAND-75-0244, Sandia National Labs, 1959.

[11]龚兴根． 电爆炸断路开关[J]． 强激光与粒子束， 2002， 14(4): 577-582． (GONG Xing-gen. Electric exploding opening switch [J]. High Power Laser and Particle Beams, 2002, 14(4) : 577-582.)

[12]王坤， 史宗谦， 石元杰， 等． 真空及空气中金属丝电爆炸特性研究[J]． 物理学报， 2017， 66(18): 185203． (WANG Kun, SHI Zong-qian, SHI Yuan-jie, et al. Characteristics of electrical explosion of single wire in a vacuum and in the air [J]. Acta Phys Sin, 2017, 66(18): 185203.)

[13]郭军， 邱爱慈． 熔丝电爆炸过程电气特性的数字仿真 [J]． 系统仿真学报， 2006， 18(1): 20-22． (GUO Jun, QIU Ai-ci. Digital simulation for fuse electrical characteristics in process of electrically exploding [J]. Journal of System Simulation, 2006, 18(1) : 20-22.)