高斯白噪声激励下粘弹性碰撞系统的稳定性

谢秀峰，李俊林，刘 迪

(1.太原科技大学 应用科学学院，太原 030024；2.山西大学 数学科学学院，太原 030006)

随着新材料、新结构的应用发展，粘弹性材料[1]被广泛用于航空航天、造船、汽车、铁路、建筑、纺织等行业。粘弹性系统的动力学行为的研究具有重要的理论意义和工程意义，引起了越来越多学者的重视。BISHOP et al[2]讨论了具有粘弹阻尼船舶模型的响应。ADHIKARI et al[3]研究了粘弹阻尼的线性振子的特征值和定性动力学特征。噪声广泛存在于实际工程中，其对系统的影响不容忽视，所以研究随机激励下粘弹性系统的相关问题受到很多学者的关注[4-6]。ARIARATNAM[7]应用随机平均方法研究了线性粘弹性系统的随机稳定性。XIE[8]研究了有界噪声激励下二维粘弹性系统的矩Lyapunov稳定性。

由碰撞、干摩擦等非光滑因素增加了动力系统的复杂性[9]，光滑系统的很多理论与成果不能直接应用到非光滑系统的分析当中。DIMENTBERG et al[10]利用Dirac delta函数和符号函数对非光滑系统进行光滑化处理，将碰撞系统转化为不含碰撞的动力系统，然后用能量平均法，分析了碰撞振动系统的随机响应问题。FENG et al[11]借助平均Poincare映射研究了随机激励下的线性碰撞振动系统。ZHAO et al[12]研究了随机激励下粘弹性碰撞系统的稳态响应。

综上所述，对于粘弹性碰撞系统的研究较少，因此有必要研究随机噪声作用下粘弹性碰撞系统的响应。本文研究了高斯白噪声激励下粘弹性碰撞系统的矩稳定性，用恢复系数来描述粘弹性碰撞前后的能量损失，结合Zhuravlev变换和随机平均法给出了系统任意阶矩Lyapunov指数。并讨论了恢复系数和粘弹性系数对系统矩稳定性的影响。

1 模型分析

考虑受高斯白噪声激励的粘弹性碰撞系统可表述为

(1)

式(1)中的粘弹性效应可表示为：

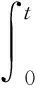
(2)

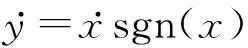
(3)

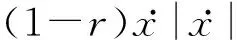
2 随机平均法

系统(3)的响应可近似表示为:

x=A(t)cosΦ(t) .

(4)

(5)

其中，Φ(t)=ωt+φ(t)，且A(t),Φ(t),φ(t)都是随机过程。系统(3)可写为关于幅值A和相位φ的随机微分关系如下:

(6)

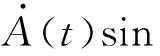
(7)

由文献[13]可知，对于一个随机系统的状态变量X(t)，其矩稳定性可以用矩Lyapunov指数Λ(p)表示

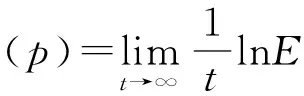
(8)

式中：E[·]表示数学期望，‖·‖2表示二阶范数，系统解p阶矩渐进稳定的充分必要条件是Λ(p)<0，并且Λ'(0)等于系统的最大Lyapunov指数

(9)

而系统的几乎必然稳定的充分必要条件是λ<0.

为了求出系统的p阶矩Lyapunov指数Λ(p)，作变换P(t)=Ap(t),并解式(6)和式(7)，得P与φ的微分关系

(10)

(11)

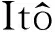
(12)

其中W(t)是标准Wiener过程，并且

推导过程见附录A.

选取Maxwell型粘弹性核函数

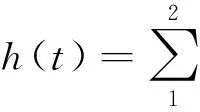
(13)

经过式(A3)和式(A4)的变换，得

(14)

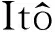
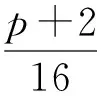
(15)

(16)

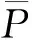
(17)

得到系统的p阶矩Lyapunov指数为

(18)

最大Lyapunov指数为

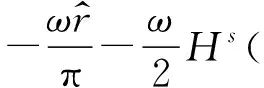
(19)

3 稳定性分析

根据式(18)的解析式给出相应的数值结果，可分析恢复因子、噪声强度和粘弹性参数对系统(1)随机稳定性的影响。图1给出系统响应的矩Lyapunov指数Λ(p)作为阶数p的函数，随不同的恢复因子r和噪声强度σ变化的函数曲线，其余系统参数为：γ1=κ1=1,γ2=κ2=0.5,β=0.5,ω=1.0,ε=0.1.实线表示由式(18)得到的解析解，虚线由Monte Carlo模拟的数值结果。该图表明，Λ(p)是p的非线性函数，在Λ(p)<0的区域内，系统响应的p阶矩渐近稳定。Λ(p)随恢复因子r的增大而增大，即r越大系统的矩稳定性越弱。Λ(p)随噪声强度σ的增大而增大，即噪声强度越大系统的矩稳定性越弱。

图1 系统(1)的p阶矩Lyapunov指数变化曲线Fig.1 The pth moment Lyapunov exponent of system (1)

图2、3分别表示矩Lyapunov指数Λ(p)随粘弹性特征参数γ,κ和阶数p的变化三维图。对于p>0，随粘弹性参数γ增大稳定区域变大，说明粘弹性越强有助于系统的稳定；而当松弛时间减小，稳定区域变窄，表明长的松弛时间有助于系统的稳定。

图2 系统响应的矩Lyapunov指数与粘弹性参数γ的变化关系Fig.2 Moment Lyapunov exponent of system with viscoelastic parameter γ

图3 系统响应的矩Lyapunov指数与粘弹性参数κ的变化关系Fig.3 Moment Lyapunov exponent of system with viscoelastic parameter κ

图4给出了矩Lyapunov指数Λ(p)与噪声强度σ和阶数p之间的函数关系。该图表明，随着噪声强度σ的增大，矩指数增大，因此，噪声强度增大使得系统响应的矩稳定性减弱。

图4 系统响应的矩Lyapunov指数与噪声强度σ的变化关系Fig.4 Moment Lyapunov exponent of system with noise intensity of σ

4 结论

本文研究了受高斯白噪声激励下粘弹性碰撞系统的随机稳定性。首先，应用Zhuravlev变换将粘弹性碰撞系统转换为非碰撞系统，然后用随机平均法得到系统的随机微分方程，求得了矩Lyapunov指数，最后通过解析结果与Monte Carlo模拟数值结果的分析，得到恢复因子、噪声强度、粘弹性参数对系统稳定性的影响。研究表明，恢复因子越大系统稳定性越弱；系统的稳定性随噪声强度的增大而减弱；随粘弹性参数的增大，稳定区域增大，随松弛时间增大，稳定区域变窄。

附录A

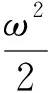
(A1)

其中

R(τ)=E[ξ(τ)ξ(t+τ)]为高斯白噪声ξ(t)的相关函数.

(A2)

应用变量代换s=t-τ和改变积分次序，得

(A3)

同理可得

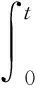
(A4)

：

[1] GURTIN M E,STERNBERG E.On the linear theory of viscoelasticity[J].Arch Ration Mech Anal,1962,11:291-356.

[2] BISHOP R E D,PRICE W G.An investigation into the linear theory of ship response to waves[J].Journal of Sound and Vibration,1979,62:353-363.

[3] ADHIKARI S,PASCUAL B.Eigenvalues of linearviscoelastic systems[J].J Sound Vib,2009,325:1000-1011.

[5] HAN X,WANG M.General decay of energy for a viscoelastic equation with nonlinear damping[J].Franklin Inst,2010,347:806-817.

[6] MESSAOUDI S A.On the control of solutions of a viscoelastic equation[J].Franklin Inst,2007,344:765-776.

[7] ARIARATNAM S T.Stochastic stability of linear viscoelastic systems[J].Probab Eng Mech,1993,8:153-155.

[8] XIE W C.Moment Lyapunov exponents of a two dimensional viscoelastic system under bounded noise excitation[J].ASME J Appl Mech,2002,69:346-357.

[9] 金栋平，胡海岩.碰撞振动与控制[M].北京：科学出版社，2005.

[10] DIMENTBERG M F,IOURTCHENKO D V.Random vibrations with impacts:a review[J].Nonlinear Dyn,2004,36:229-254.

[11] FENG J Q,XU W,RONG H W,et al.Stochastic responses of Duffing-van der Pol vibro-impact system under additive and multiplicative random excitations[J].Int J Non-linear Mech,2009,44:51-57.

[12] ZHAO X R,XU W,GU X D,et al.Stochastic stationary responses of a viscoelastic system with impacts under additive Gaussian white noise excitation[J].Physica A,2015,431:128-139.

[13] ARNOLD L.A formula connection sample and moment stability of linear stochastic systems[J].SIAM Journal of Applied Mathematics，1984，44：793-802.

[14] 朱位秋.随机振动[M].北京：科学出版社，1992.