铁路路堑型明洞顶部垂直土压力的研究
2018-05-30王云震邹春棋
王云震,李 哲,于 丽,邹春棋,王 亮
(1.中铁二十四局集团有限公司,上海 200071;2.西南交通大学土木工程学院,成都 610031;3.西南交通大学交通隧道工程教育部重点实验室,成都 610031)
山岭隧道修建的环境山岭连绵,沟谷发育,在沟谷地段遇到浅埋或超浅埋情况,明洞结构被广泛使用。但是由于受到地形限制或平山造地政策的影响,浅埋明洞回填深度可能较大。关于明洞拱圈垂直土压力,《铁路隧道设计规范》(TB10003—2005)采用土柱法计算。土柱法仅适用于回填高度较低的情况而规范并未对回填土高度做出明确规定,所以简单使用土柱法不能满足工程安全与经济的要求。
关于回填土压力,现有研究主要集中在涵洞方面[1-9],对隧道方面关注较少[9-14]。由于隧道与涵洞空间尺寸水平不同,回填土压力规律也不尽相同,且现有理论少有对回填偏压的情况进行研究。为此,借鉴高填土涵洞(管)的研究思路及部分成果,基于Marston理论推导出路堑型明洞拱顶垂直土压力计算方法并进行数值模拟分析,研究浅埋情况(0~2倍洞高,取0~25 m)下拱顶土压力大小以及拱部土压力的分布规律。
1 路堑对称型明洞拱顶垂直土压力理论计算
1.1 计算模型
隧道为带状构筑物,选取轴向单位长度的隧道进行分析,如图1所示。明洞结构刚度大而洞侧填土的刚度小,因此外土柱Ⅱ的沉降量大于内土柱Ⅰ的沉降量,外土柱对内土柱产生向下的摩擦力从而形成隧道拱部的附加土压力。随着回填施工的进行,内外土柱沉降差渐渐被弥补,在填土高度为Hc时变为零,将此时的回填平面称为等沉面。
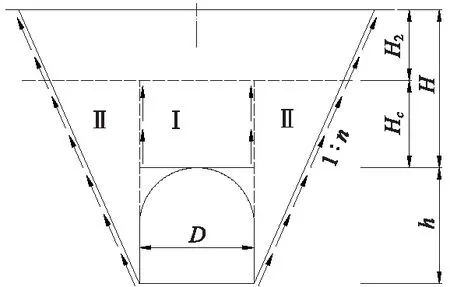
图1 路堑对称型明洞回填模型示意
在等沉面以下存在土柱间摩擦力而等沉面以上不存在,所以对不同填土高度下的土压力进行研究,利用水平层分析法[15]可以解得相关土压力、拱顶的总土压力及拱顶土压力系数。
1.2 H

图2 计算简图
dW+b(dq1)-2τ(dh1)=0
(1)
整理式(1)得
(2)
式中,b=mh+mH-mh1。
根据h1=0,q1=0的边界条件,解得
(3)
式中,b2=b1+mh,b1=mh。
沿土体Ⅰ、Ⅱ的交界面对剪应力τ进行积分,得拱顶的附加土压力
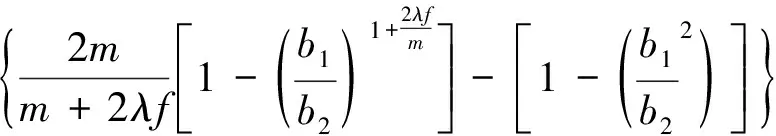
(4)
拱顶总土压力为P1=DHγ+F1,相应的土压力系数
(5)
1.3 H>Hc情况
同1.2方法相同,在等沉面以上H2段列竖向力的平衡方程并求解,可得等沉面上的平均垂直土压力
(6)
式中,B3=D+2m(Hc+h);Bs=B3=2mH2。
在等沉面以下土体Ⅱ的深度h1处,取水平微分单元,单元宽度b=b1+m(Hc-h1),列竖向力的平衡方程,由h1=0,q=q2的边界条件得解
(7)
式中,b3=b1+mHc。
洞顶附加土压力
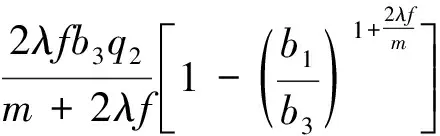
(8)
拱顶总土压力P2=γDHc+q2D+F2,相应的土压力系数
(9)
1.4 等沉面高度Hc
H≥Hc时,令内外土柱压缩量相等即可得等沉面高度Hc。

(10)
土体Ⅱ的总压缩量近似为
(11)
由变形协调条件Δ1=Δ2和边界条件H2=0、q2=0可解得Hc。
2 路堑偏压型明洞拱顶垂直土压力理论计算
2.1 计算模型
计算模型如图3所示,原理与前文1.1中相同,同时本文假定等沉面的高度不受回填偏压的影响,因此路堑偏压型等沉面高度与路堑对称型计算方法相同。随着回填深度增加,根据回填土状态不同,分情况推导拱顶土压力计算公式。

图3 路堑偏压型明洞回填模型示意
2.2H2计算简图如图4所示。此时,两侧外土柱状态相同,均低于等沉面,计算过程相同。对边界条件进行简化,假定上部阴影部分土体的重力均匀分布在h1=0的边界上:q1=Q1,其中
(12)
根据边界条件解得q1,进一步求得左侧外土柱对拱顶的附加土压力
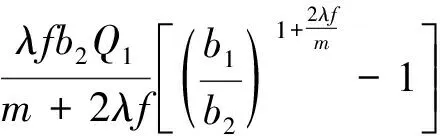
(13)
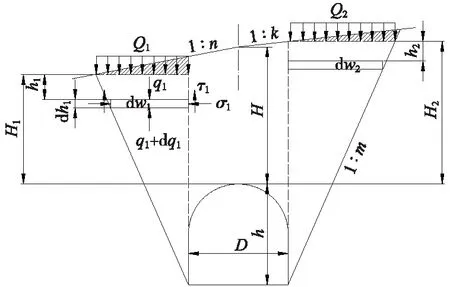
图4 H2同理可得右侧外土柱对拱顶的附加土压力F2。
洞顶总土压力
P1=DHγ+F1+F2
(14)
相应的土压力系数
(15)
2.3 H2>Hc且H1计算简图如图5所示,左侧外土柱低于等沉面,带来的拱顶附加土压力F1公式不变;右侧外土柱高于等沉面,相应的拱顶附加土压力F2公式改变。

图5 H2>Hc且H1对右侧外土柱,首先计算附加压力Q2。
等沉面以上土体划分为两层:一层为三角土体,一层为梯形土体。计算简图如图6所示。对梯形土体列极限平衡方程,根据边界条件,解得
(16)
式中,b2=b1+mH2,b1=mh。
其次,计算等沉面以下任意深度土压力q2。
根据h2=0,q2=Q2,的边界条件,解得
(17)
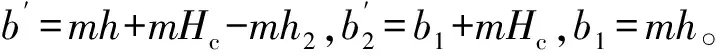
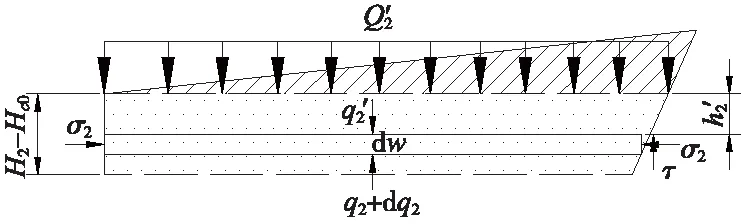
图6 等沉面以上土体计算简图
最后,计算拱顶附加土压力F2

(18)
根据式(14)和式(15)得到拱顶土压力及土压力系数。
2.4 H1>Hc的情况
此时,两侧外土柱状态相同,均高于等沉面,推导过程与2.3中右侧外土柱相同。同样根据式(14)和式(15)求得拱顶土压力及土压力系数。
3 拱顶土压力分析
3.1 理论计算与有限元计算结果对比
新建九景衢铁路某隧道明洞段长35 m,明挖段位于沟谷地区,围岩级别为Ⅴ级。明洞跨度13.7 m,高11 m,最大埋深处12 m。
采用ANSYS对该断面进行三维数值模拟,岩土体及明洞结构物理力学参数如表1所示。岩土体采用Drucker-Prager模型,服从Drucker-Prager屈服准则。路堑与回填土、明洞结构与回填土的接触单元摩擦参数均取tanφ。
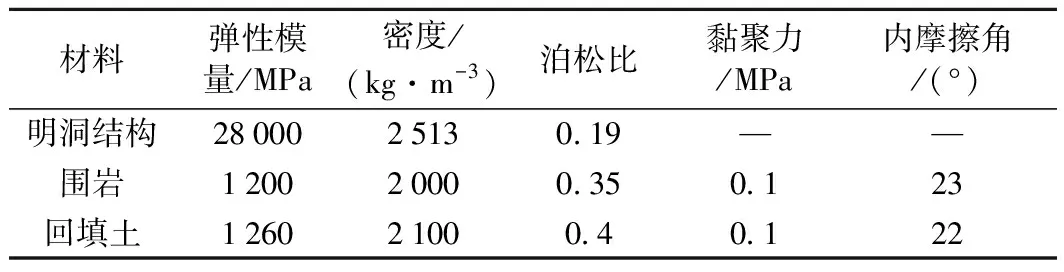
表1 物理力学参数
(1)路堑对称型明洞
由公式计算和有限元计算得到拱顶土压力及土压力系数变化如图7、图8所示。

图7 计算土压力与有限元计算结果比较
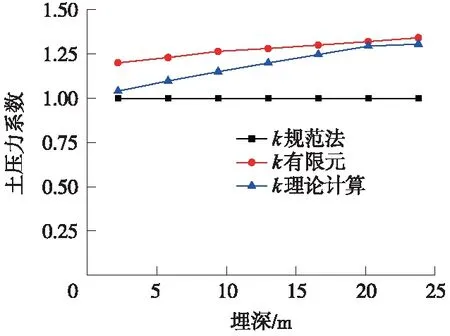
图8 计算土压力系数与有限元计算结果比较
由图7可知,在回填土厚度在0~25 m的范围内,理论计算结果与有限元计算结果吻合较好,相差在5%之内。理论计算和有限元计算结果均大于规范法的土柱重,差值随回填土厚度的增加而增加。由图8可知,在埋深0~15 m范围内,有限元土压力系数比理论计算结果大,差值在15%以内;在埋深15~25 m范围内,有限元土压力系数稍大于理论计算结果,差值在5%以内;从整体上看,理论计算的土压力系数与有限元结果吻合良好。
(2)路堑偏压型明洞
填土坡度为1∶5时,由公式计算和有限元计算得到拱顶土压力及土压力系数变化如图9、图10所示。
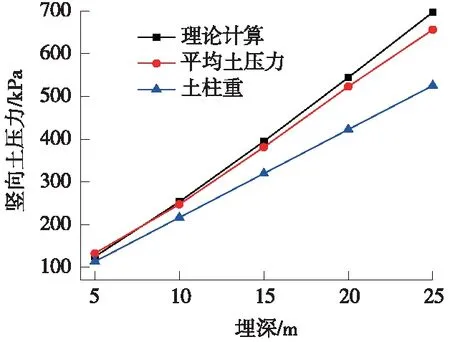
图9 路堑偏压型计算土压力与有限元结果比较
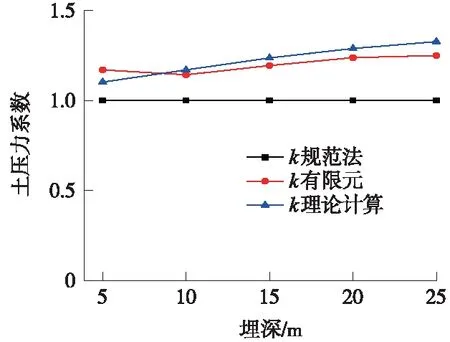
图10 路堑偏压型计算土压力系数与有限元计算结果比较
由图9可知,在回填土厚度在0~25 m的范围内,理论计算结果与有限元计算结果吻合较好,相差在5%之内。理论计算与有限元计算结果均大于规范法的土柱重,差值随回填土厚度的增加而增加。由图10可知,理论计算与有限元计算结果吻合较好,相差在7%之内。在埋深0~5 m范围内,有限元计算结果比理论计算结果大,而在埋深10~25 m范围内,有限元计算结果稍小。
3.2 拱部土压力分布规律
(1)路堑对称型明洞
在有限元模型拱部上设置均匀分布的接触压力提取点,将提取的接触压力转化为垂直土压力。根据结果可以发现:明洞所受的垂直土压力主要集中在拱部结构的中部,在拱脚部位垂直土压力较小,且两侧受力对称。
取节点垂直土压力分布系数
式中,qi为节点i处的竖向土压力;q0为拱顶处的竖向土压力。
由于荷载对称,对拱部中轴线左侧节点的垂直土压力进行分析。计算节点垂直土压力分布系数,绘制图11。由图11可以看出,在明洞埋深10 m以下时,拱肩部位的垂直土压力大于拱顶垂直土压力;在明洞埋深大于10 m时,拱肩部位的垂直土压力略小于拱顶土压力,分布系数曲线整体平缓,且各节点垂直土压力分布系数随埋深增大而趋于稳定。整理稳定后分布系数得到拱部垂直土压力分布情况如图12所示。
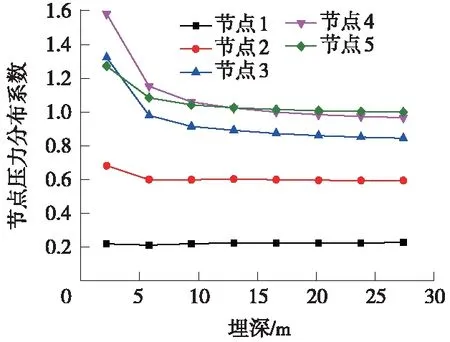
图11 各节点压力分布系数随埋深的变化
(2)路堑偏压型明洞
填土坡度为1∶5时,将提取的接触压力转化为垂直土压力。根据结果可以发现:路堑偏压明洞所受的垂直土压力主要集中在拱部结构的中部,在拱脚部位垂直土压力较小,且右侧(偏压侧)拱脚所受的压力大于左侧拱脚所受的压力。求得各节点的垂直土压力分布系数,计算对称位置节点的分布系数差值(偏压侧减对侧)绘制表2。

图12 路堑对称型垂直土压力分布情况

表2 不同埋深下对称节点分布系数之差
由表2可知:拱部中部节点(节点4~节点8)的垂直土压力受偏压地质条件影响较小,对称的节点差异很小;拱肩部位节点(节点9、节点3)的垂直土压力分布系数差异在0.1范围内,随埋深的增加而减小;拱脚部位节点(节点7、节点8、节点5、节点4)的压力分布系数差异较大,埋深5 m时差异高达0.4,差异随埋深的增加而减小,在埋深为25 m时,差异值在0.1左右。
3.3 不同埋深下拱顶垂直土压力系数
考虑土压力计算方法10%的误差范围,综合两种路堑型明洞拱顶垂直土压力计算给出不同埋深下路堑型明洞拱顶垂直土压力系数取值情况,见表3。
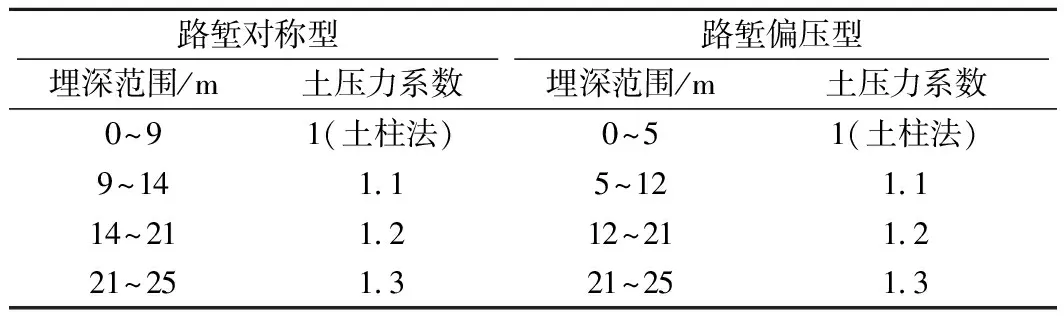
表3 不同埋深下拱顶垂直土压力系数
由表3可以看出,两种路堑型明洞在回填埋深0~14 m的范围内拱顶土压力系数的取值不尽相同,而在14~25 m的范围内取值相同。
4 结论
基于Marston理论考虑明洞拱顶上内、外土柱变形差异以及偏压回填情况,建立了路堑型明洞拱顶土压力计算模型和计算公式,给出了浅埋情况下不同埋深土压力系数的取值,理论计算与有限元计算结果相吻合。
(1)路堑型明洞拱顶垂直土压力变化趋势为先增大后减小。
(2)埋深大于10 m时,路堑对称型明洞拱部垂直土压力的分布规律不再随埋深改变而发生变化;路堑偏压型的分布规律则随埋深变化而变化,埋深增大两侧土压力分布系数差值越小。
(3)两种路堑型明洞在回填埋深0~14 m的范围内拱顶土压力系数的取值不尽相同,而在14~25 m的范围内取值相同。
[1] 李自寅.上埋式涵洞土压力的计算[J].铁道标准设计通讯,1979(10):11-15.
[2] 严东方,林从谋.上埋式涵洞顶部垂直土压力计算方法[J].地下空间与工程学报,2007,3(2):245-248.
[3] 李永刚,李珠,张善元.矩形沟埋涵洞顶部垂直土压力[J].工程力学,2008,25(1):155-160.
[4] 陈保国,郑俊杰.高路堤下涵洞地基处理现场测试与数值模拟研究[J].岩土力学,2009,30(5):1483-1489.
[5] Garg, Anil K, Abolm aali. Ali Finite element modeling and analysis of reinforced concrete box culverts[J]. Journal of Transportation Engineering, 2009,135(3):121-128.
[6] 李永刚,刘孝俊,周泽涛.梯形沟埋涵洞顶部垂直土压力试验研究[J].太原理工大学学报,2011(6):654-659.
[7] 陈保国,焦俊杰,宋丁豹.钢筋混凝土箱涵竖向土压力理论研究——梯形沟谷设涵[J].岩土力学,2013(10):2911-2918.
[8] 赵建斌,申俊敏,董立山.高填方涵洞受力特性现场测试及数值模拟研究[J].郑州大学学报(工学版),2014(3):111-115.
[9] 周兴涛,陈保国,简文星,等.沟埋涵洞土拱效应及涵顶垂直土压力研究[J].地下空间与工程学报,2015(4):957-964.
[10] 赵鹏,王起才,李盛,等.明洞顶垂直土压力性状及土工格栅减载方案研究[J].兰州交通大学学报,2013(4):79-84.
[11] 李盛,王起才,马莉,等.黄土地区高填土明洞土拱效应及土压力减载计算[J].岩石力学与工程学报,2014(5):1055-1062.
[12] 旷文涛.超高回填明洞设计探讨[J].铁道标准设计,2014(7):112-115.
[13] 刘强,谭忠盛,陈立保,等.明洞填土压力计算模式不定性的现场测试研究[J].现代隧道技术,2015(2):128-134.
[14] 李盛,马莉,王起才,等.高填明洞土压力计算方法及其影响因素研究[J].中国铁道科学,2016(5):41-49.
[15] Handy R L. The arch in soil arching [J]. Journal of Geotechnical Engineering, 1985,111(3):302-318.


图2 计算简图
dW+b(dq1)-2τ(dh1)=0
(1)
整理式(1)得
(2)
式中,b=mh+mH-mh1。
根据h1=0,q1=0的边界条件,解得
(3)
式中,b2=b1+mh,b1=mh。
沿土体Ⅰ、Ⅱ的交界面对剪应力τ进行积分,得拱顶的附加土压力
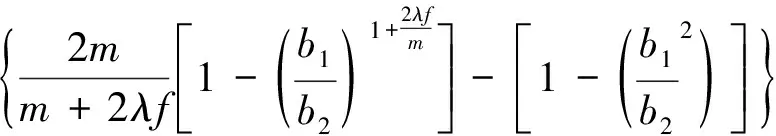
(4)
拱顶总土压力为P1=DHγ+F1,相应的土压力系数
(5)
1.3 H>Hc情况
同1.2方法相同,在等沉面以上H2段列竖向力的平衡方程并求解,可得等沉面上的平均垂直土压力
(6)
式中,B3=D+2m(Hc+h);Bs=B3=2mH2。
在等沉面以下土体Ⅱ的深度h1处,取水平微分单元,单元宽度b=b1+m(Hc-h1),列竖向力的平衡方程,由h1=0,q=q2的边界条件得解
(7)
式中,b3=b1+mHc。
洞顶附加土压力
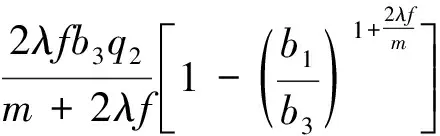
(8)
拱顶总土压力P2=γDHc+q2D+F2,相应的土压力系数
(9)
1.4 等沉面高度Hc
H≥Hc时,令内外土柱压缩量相等即可得等沉面高度Hc。

(10)
土体Ⅱ的总压缩量近似为
(11)
由变形协调条件Δ1=Δ2和边界条件H2=0、q2=0可解得Hc。
2 路堑偏压型明洞拱顶垂直土压力理论计算
2.1 计算模型
计算模型如图3所示,原理与前文1.1中相同,同时本文假定等沉面的高度不受回填偏压的影响,因此路堑偏压型等沉面高度与路堑对称型计算方法相同。随着回填深度增加,根据回填土状态不同,分情况推导拱顶土压力计算公式。

图3 路堑偏压型明洞回填模型示意
2.2H2 计算简图如图4所示。此时,两侧外土柱状态相同,均低于等沉面,计算过程相同。对边界条件进行简化,假定上部阴影部分土体的重力均匀分布在h1=0的边界上:q1=Q1,其中 (12) 根据边界条件解得q1,进一步求得左侧外土柱对拱顶的附加土压力 (13) 图4 H2 同理可得右侧外土柱对拱顶的附加土压力F2。 洞顶总土压力 P1=DHγ+F1+F2 (14) 相应的土压力系数 (15) 计算简图如图5所示,左侧外土柱低于等沉面,带来的拱顶附加土压力F1公式不变;右侧外土柱高于等沉面,相应的拱顶附加土压力F2公式改变。 图5 H2>Hc且H1 对右侧外土柱,首先计算附加压力Q2。 等沉面以上土体划分为两层:一层为三角土体,一层为梯形土体。计算简图如图6所示。对梯形土体列极限平衡方程,根据边界条件,解得 (16) 式中,b2=b1+mH2,b1=mh。 其次,计算等沉面以下任意深度土压力q2。 根据h2=0,q2=Q2,的边界条件,解得 (17) 图6 等沉面以上土体计算简图 最后,计算拱顶附加土压力F2 (18) 根据式(14)和式(15)得到拱顶土压力及土压力系数。 此时,两侧外土柱状态相同,均高于等沉面,推导过程与2.3中右侧外土柱相同。同样根据式(14)和式(15)求得拱顶土压力及土压力系数。 新建九景衢铁路某隧道明洞段长35 m,明挖段位于沟谷地区,围岩级别为Ⅴ级。明洞跨度13.7 m,高11 m,最大埋深处12 m。 采用ANSYS对该断面进行三维数值模拟,岩土体及明洞结构物理力学参数如表1所示。岩土体采用Drucker-Prager模型,服从Drucker-Prager屈服准则。路堑与回填土、明洞结构与回填土的接触单元摩擦参数均取tanφ。 表1 物理力学参数 (1)路堑对称型明洞 由公式计算和有限元计算得到拱顶土压力及土压力系数变化如图7、图8所示。 图7 计算土压力与有限元计算结果比较 图8 计算土压力系数与有限元计算结果比较 由图7可知,在回填土厚度在0~25 m的范围内,理论计算结果与有限元计算结果吻合较好,相差在5%之内。理论计算和有限元计算结果均大于规范法的土柱重,差值随回填土厚度的增加而增加。由图8可知,在埋深0~15 m范围内,有限元土压力系数比理论计算结果大,差值在15%以内;在埋深15~25 m范围内,有限元土压力系数稍大于理论计算结果,差值在5%以内;从整体上看,理论计算的土压力系数与有限元结果吻合良好。 (2)路堑偏压型明洞 填土坡度为1∶5时,由公式计算和有限元计算得到拱顶土压力及土压力系数变化如图9、图10所示。 图9 路堑偏压型计算土压力与有限元结果比较 图10 路堑偏压型计算土压力系数与有限元计算结果比较 由图9可知,在回填土厚度在0~25 m的范围内,理论计算结果与有限元计算结果吻合较好,相差在5%之内。理论计算与有限元计算结果均大于规范法的土柱重,差值随回填土厚度的增加而增加。由图10可知,理论计算与有限元计算结果吻合较好,相差在7%之内。在埋深0~5 m范围内,有限元计算结果比理论计算结果大,而在埋深10~25 m范围内,有限元计算结果稍小。 (1)路堑对称型明洞 在有限元模型拱部上设置均匀分布的接触压力提取点,将提取的接触压力转化为垂直土压力。根据结果可以发现:明洞所受的垂直土压力主要集中在拱部结构的中部,在拱脚部位垂直土压力较小,且两侧受力对称。 取节点垂直土压力分布系数 式中,qi为节点i处的竖向土压力;q0为拱顶处的竖向土压力。 由于荷载对称,对拱部中轴线左侧节点的垂直土压力进行分析。计算节点垂直土压力分布系数,绘制图11。由图11可以看出,在明洞埋深10 m以下时,拱肩部位的垂直土压力大于拱顶垂直土压力;在明洞埋深大于10 m时,拱肩部位的垂直土压力略小于拱顶土压力,分布系数曲线整体平缓,且各节点垂直土压力分布系数随埋深增大而趋于稳定。整理稳定后分布系数得到拱部垂直土压力分布情况如图12所示。 图11 各节点压力分布系数随埋深的变化 (2)路堑偏压型明洞 填土坡度为1∶5时,将提取的接触压力转化为垂直土压力。根据结果可以发现:路堑偏压明洞所受的垂直土压力主要集中在拱部结构的中部,在拱脚部位垂直土压力较小,且右侧(偏压侧)拱脚所受的压力大于左侧拱脚所受的压力。求得各节点的垂直土压力分布系数,计算对称位置节点的分布系数差值(偏压侧减对侧)绘制表2。 图12 路堑对称型垂直土压力分布情况 表2 不同埋深下对称节点分布系数之差 由表2可知:拱部中部节点(节点4~节点8)的垂直土压力受偏压地质条件影响较小,对称的节点差异很小;拱肩部位节点(节点9、节点3)的垂直土压力分布系数差异在0.1范围内,随埋深的增加而减小;拱脚部位节点(节点7、节点8、节点5、节点4)的压力分布系数差异较大,埋深5 m时差异高达0.4,差异随埋深的增加而减小,在埋深为25 m时,差异值在0.1左右。 考虑土压力计算方法10%的误差范围,综合两种路堑型明洞拱顶垂直土压力计算给出不同埋深下路堑型明洞拱顶垂直土压力系数取值情况,见表3。 表3 不同埋深下拱顶垂直土压力系数 由表3可以看出,两种路堑型明洞在回填埋深0~14 m的范围内拱顶土压力系数的取值不尽相同,而在14~25 m的范围内取值相同。 基于Marston理论考虑明洞拱顶上内、外土柱变形差异以及偏压回填情况,建立了路堑型明洞拱顶土压力计算模型和计算公式,给出了浅埋情况下不同埋深土压力系数的取值,理论计算与有限元计算结果相吻合。 (1)路堑型明洞拱顶垂直土压力变化趋势为先增大后减小。 (2)埋深大于10 m时,路堑对称型明洞拱部垂直土压力的分布规律不再随埋深改变而发生变化;路堑偏压型的分布规律则随埋深变化而变化,埋深增大两侧土压力分布系数差值越小。 (3)两种路堑型明洞在回填埋深0~14 m的范围内拱顶土压力系数的取值不尽相同,而在14~25 m的范围内取值相同。 [1] 李自寅.上埋式涵洞土压力的计算[J].铁道标准设计通讯,1979(10):11-15. [2] 严东方,林从谋.上埋式涵洞顶部垂直土压力计算方法[J].地下空间与工程学报,2007,3(2):245-248. [3] 李永刚,李珠,张善元.矩形沟埋涵洞顶部垂直土压力[J].工程力学,2008,25(1):155-160. [4] 陈保国,郑俊杰.高路堤下涵洞地基处理现场测试与数值模拟研究[J].岩土力学,2009,30(5):1483-1489. [5] Garg, Anil K, Abolm aali. Ali Finite element modeling and analysis of reinforced concrete box culverts[J]. Journal of Transportation Engineering, 2009,135(3):121-128. [6] 李永刚,刘孝俊,周泽涛.梯形沟埋涵洞顶部垂直土压力试验研究[J].太原理工大学学报,2011(6):654-659. [7] 陈保国,焦俊杰,宋丁豹.钢筋混凝土箱涵竖向土压力理论研究——梯形沟谷设涵[J].岩土力学,2013(10):2911-2918. [8] 赵建斌,申俊敏,董立山.高填方涵洞受力特性现场测试及数值模拟研究[J].郑州大学学报(工学版),2014(3):111-115. [9] 周兴涛,陈保国,简文星,等.沟埋涵洞土拱效应及涵顶垂直土压力研究[J].地下空间与工程学报,2015(4):957-964. [10] 赵鹏,王起才,李盛,等.明洞顶垂直土压力性状及土工格栅减载方案研究[J].兰州交通大学学报,2013(4):79-84. [11] 李盛,王起才,马莉,等.黄土地区高填土明洞土拱效应及土压力减载计算[J].岩石力学与工程学报,2014(5):1055-1062. [12] 旷文涛.超高回填明洞设计探讨[J].铁道标准设计,2014(7):112-115. [13] 刘强,谭忠盛,陈立保,等.明洞填土压力计算模式不定性的现场测试研究[J].现代隧道技术,2015(2):128-134. [14] 李盛,马莉,王起才,等.高填明洞土压力计算方法及其影响因素研究[J].中国铁道科学,2016(5):41-49. [15] Handy R L. The arch in soil arching [J]. Journal of Geotechnical Engineering, 1985,111(3):302-318.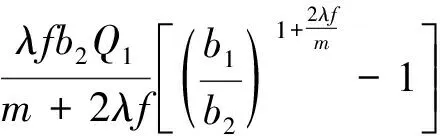

2.3 H2>Hc且H1

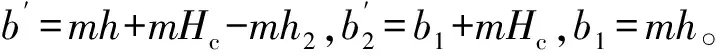


2.4 H1>Hc的情况
3 拱顶土压力分析
3.1 理论计算与有限元计算结果对比





3.2 拱部土压力分布规律



3.3 不同埋深下拱顶垂直土压力系数

4 结论
