基于模糊故障树的列控风险发生频率研究

郭荣昌，赵小娟，范多旺

(兰州交通大学自动化与电气工程学院，兰州 730070)

随着我国高铁里程的增长和运营速度的提高，高铁运营安全越来越凸显其重要地位。作为高铁核心装备和安全相关系统的列车运行控制系统[1]，直接影响高铁安全。风险发生频率等级评价是列控风险评价的重要内容之一[2-3]。对列控风险发生频率进行评价，是当前的一个研究热点。

目前，对列控风险发生频率分析的方法主要有定性法、半定性半定量法[4]、定量法[5-8]和模型检验法[9]。

定性法主要是指根据专家经验直接判断危险源的风险发生频率等级，此方法虽然简单易操作，但当专家面临列控系统这种涉及人机环管的复杂系统时，有时也难以进行精确的评判。半定性半定量法是将定性评判和定量计算结合起来，文献[4]对专家评判方法进行了一些改进，提出了一种基于HAUSDORFF距离的模糊群决策的发生频率计算模型，该方法降低了专家评判结果的主观程度。定量法主要是建立风险故障树，通过定量计算风险事件的发生概率或频率来得到结果。但由于我国列控运营的相关数据较为薄弱，失效数据、环境影响数据等相关的数据较为匿乏，因而故障树底事件的相关数据较难获取，这影响了定量法的应用。模型检验法是一种通过建立系统的统计模型，然后对统计模型进行统计计算，最后得到系统的发生频率、危险失效率等相关统计信息的方法。模型检验法在分析小概率事件发生频率上尚处于起步阶段，还没有形成系统的建模和分析方法。文献[9]提出了一种改进的统计模型检测方法来计算列车碰撞事件发生概率，虽然该方法能对列车碰撞事件的发生频率进行统计，但是难以应用于实际。

为了提高专家评价的准确性，采用基于模糊故障树的发生频率评价方法。用故障树对发生频率事件进行描述，对于有统计数据信息的基本事件的发生频率采用精确值表示，对于基本事件中没有统计数据信息的事件的发生频率采用模糊数表示，采用三角模糊判断矩阵得到专家权重，利用模糊算子对顶事件的发生频率进行计算，得到顶事件的模糊数，最后将顶事件的模糊数精确化得到顶事件的发生频率等级。

1 故障树和模糊数介绍

1.1 故障树介绍

故障树分析方法是一种通过演绎方式来分析系统安全的方法。它将系统可能发生或已经发生的事故(顶事件)作为分析起点，将导致事故的原因事件按因果逻辑关系逐层列出，用树形图表示出来，构成一种逻辑模型。

当故障树结构模型中存在出现次数大于1的基本事件时，可通过最小割集来求顶事件发生的概率。假定故障树的第i个最小割集可以表示为MCi，且最小割集之间相互独立，则顶事件发生的概率可以表示为

(1)

当最小割集之间不是相互独立时，应用容斥定理计算顶事件发生的概率，有

P(T)=P(MC1∪MC2∪MC3…∪MCk)=

(-1)k-1P(MC1∩MC2∩MC3…∩MCk)

(2)

1.2 模糊数介绍

模糊集理论是由扎德在1965年提出的用来处理现象不精确和模糊的问题。模糊数用于处理如“接近1或者0”、“可靠度、安全度比较低”、“故障率较高”等不精确信息。模糊数的隶属函数有多种，如三角模糊数、梯形模糊数、正态模糊数等，它们的隶属函数形式可见相关文献，本文不再详述。

通过各种途径获得的故障事件发生概率有多种形式，包括精确发生概率值、语言值及各种模糊数。为了便于故障树分析，应将它们归一为一种形式。

1.2.1 模糊数归一化

1.2.2 模糊数运算

(1)加法运算⊕

(2)减法运算Θ

(3)乘法运算⊗

(4)与门(and)、或门(or)运算

1-(1-b1)(1-b2)，1-(1-c1)(1-c2)，

1-(1-d1)(1-d2))

2 模糊故障树分析方法介绍

传统故障树分析方法是以基本事件发生的概率已知为前提的。当基本事件发生的概率尚未确定时，无法通过传统的故障树方法对系统的风险进行有效的评估。此时，借助专家判断，采用模糊故障树分析方法，可以准确地评估系统发生的概率[11]。

图1 基于模糊故障树的发生频率计算方法

基于模糊数的发生频率计算方法如图1所示。从图1可以看出，模糊故障树计算方法共有3个步骤，分别是构造故障树、基本事件分类及发生频率模糊数计算和顶事件发生频率模糊数计算及去模糊化。

2.1 构造故障树

将需要进行发生频率等级评价的风险作为顶事件，依据铁路相关规范和专家经验等来构造故障树。

2.2 基本事件分类和发生频率模糊数计算

将故障树中的基本事件分为没有发生频率精确值的基本事件和有发生频率精确值的基本事件。

对于有发生频率精确值的基本事件，将精确值直接转换为梯形模糊数。

当基本事件发生频率没有精确值时，需要借助专家意见，专家给出对于某基本事件发生频率的判断，专家评判结果以语言变量的形式表示。参考EN标准[12]中给出的发生频率等级表，另外考虑到鲁棒性，隶属函数之间应有重叠，且重叠一般为25%～50%[13]，如表1所示。

表1 语言评判结果和梯形模糊数的对照

从不同的专家获得的评判结果不尽相同，这就需要对专家权重进行计算，然后综合专家的评判结果得出最终的基本事件发生频率评判结果。计算专家权重一般采用层次分析法等主观评价方法和熵权法等客观评价方法。层次分析法在遇到因素众多、规模较大的问题时，容易出现判断矩阵难以满足一致性要求的问题，而且元素间两两比较判断的次数就越多，很难达到一致[14，15]。东北大学郭亚军对层次分析法进行了改进，提出了G1法，该方法避开了层次分析法的缺点，而且无需一致性检验[16]。本文采用G1法来计算专家权重，依据文献[16]，计算步骤如下。

(1)确定序关系

对做出评价的专家进行一个排序，按照重要度从高到低进行排序。用Ek表示排序为第k的专家，则序关系可以表示为{E1，E2，…，EK}，K表示专家总数。

(2)相邻专家重要度确定

用Wk表示排序为第k的专家的权重，排序为k-1的专家Ek-1和排序为k的专家Ek之间的重要程度之比可以用Rk=Wk-1/Wk来表示，其中Rk的取值需要参考表2。

表2 G1法重要度描述

(3)专家权重计算

显然有

(3)

Wk-1=RkWk

(4)

2.3 顶事件发生频率模糊数计算和去模糊化

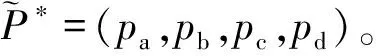
采用重心法[17]对顶事件模糊数去模糊化，得到顶事件发生频率的精确概值P*

(5)

参考表1，得到顶事件发生频率等级。

3 实例

列控系统狭义上讲包括地面设备和车载设备，但是从广义上讲不仅包含地面设备和车载设备，还包括联锁、调度等。道岔是联锁系统中的关键设备，道岔的安全性直接关系着行车效率和安全。以文献[18]中的道岔四开位置采集为定位为例的例子进行计算。故障树采用文献[18]建立的故障树，如图2所示。

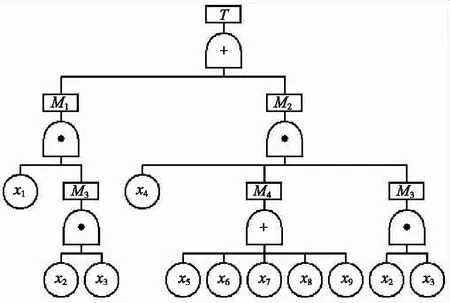
图2 道岔四开位置采集为定位故障树

3.1 构造故障树

图2中的事件名称见表3。

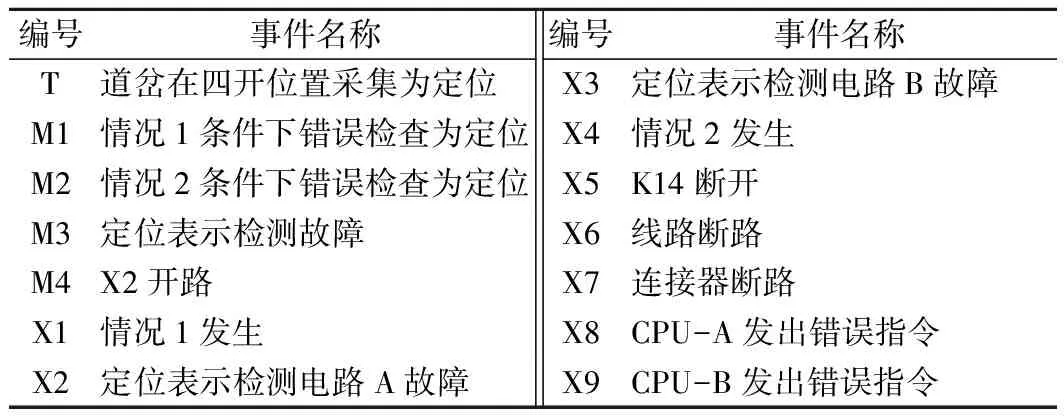
表3 事件编号和事件名称表

3.2 基本事件分类和发生频率模糊数计算

为了验证基于模糊数概率计算方法的正确性，假定所有的基本事件都没有精确的统计数据，均需要进行评判。请铁路信号领域的6名专家和4名现场维护人员对基本事件进行评判。

3.2.1 人员权重计算

对6名专家和4名维护人员进行重要度排序，排序结果为{E1，E2，…，E10}。

3.2.2 发生频率计算

邀请10个专家分别对基本事件的发生频率进行评估，评估结果为语言值，具体的评估结果这里不再叙述。

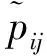
同理，也可得到其他基本事件的模糊数。

3.3 顶事件发生频率模糊数计算和去模糊化

采用下行法计算最小割集，结果为：MC1={X1，X2，X3}，MC2={X2，X3，X4，X5}，MC3={X2，X3，X4，X6}，MC4={X2，X3，X4，X7}，MC5={X2，X3，X4，X8}，MC6={X2，X3，X4，X9}。

依据与或模糊算子，得到顶事件模糊数；并依据式(5)，计算得到精确值为P*=7.21×10-13。

对应表1，可以得到评估结果为几乎不可能的。

上例中基本事件都是需要专家进行评价的，若部分基本事件有精确值，本文验证在此情况下的算法的正确性。采用文献[18]中的数据，认为基本事件X1，X2，X3有精确值，对顶事件进行计算，得到结果6.21×10-14。认为基本事件X1，X2，X3，X4，X5，X6，X7，X8， X9均有精确值，计算结果为P*=7.4077×10-17。文献[18]中的精确计算结果为7.407 7×10-17。比较计算结果可以看出，如果基本事件中精确值越多，则计算结果越精确；如果所有基本事件都由专家进行评价，虽然评估结果值与精确值之间存在差距，但是从发生频率等级来看，二者是一致的。这也证明了本文算法的可行性和有效性。

4 结论

本文引入模糊数，采用模糊故障树对列控风险发生频率等级进行计算。首先将需要进行发生频率评价的列控风险表示成故障树的形式，之后对基本事件分类，并用模糊数来表示基本事件的发生频率，然后计算得到需要评价的列控风险的模糊数，最后通过去模糊化得到精确发生频率值，并确定风险发生频率等级。实例验证了本文采用的模糊故障树计算方法的合理性和有效性。

[1] 宁滨，唐涛，李开成，等.高速列车运行控制系统[M].北京:科学出版社，2012：303.

[2] 张跃兵，王凯，王志亮.危险源理论研究及在事故预防中的应用[J].中国安全科学学报，2011，21(6):10-16.

[3] 侯志强，刘敏燕，彭思义，等.水运工程施工重大危险源风险评价关键技术研究[J].中国安全科学学报，2009，19(5):135-139.

[4] 张亚东，郭进，戴贤春，等.列车运行控制系统风险发生频率的分析模型研究[J].中国安全科学学报，2012，22(9):37-42.

[5] 张苑，刘朝英，李启翮，等.无线闭塞中心系统安全风险分析及对策[J].中国铁道科学，2010，31(4):112-117.

[6] 刘敬辉，戴贤春，郭湛，等.铁路系统基于风险的定量安全评估方法[J].中国铁道科学，2009，30(5):123-128.

[7] 肖礼谆，马驷，甄利贤.高速铁路客运站风险分析研究[J].铁道运输与经济，2014，36(9):57-62.

[8] 邱敏.基于动态故障树的列控系统风险分析与控制[D].成都:西南交通大学，2014.

[9] 杜德慧，程贝，刘静.面向安全攸关系统中小概率事件的统计模型检测[J].软件学报，2015，26(2):305-320.

[10] 武庄，石柱，何新贵.基于模糊集合论的故障树分析方法及其应用[J].系统工程与电子技术，2000，22(9):72-75.

[11] 董海波，顾学康.基于模糊故障树方法的钻井平台井喷概率计算[J].中国造船，2013，54(1):155-165.

[12] IEC C / S C T. Iec 62278—2002， Railway Applications-Specification and Demonstration of Reliability， Availability[S]. 2007.

[13] 吕琛.故障诊断与预测—原理、技术及应用[M].北京：北京航空航天大学出版社，2012：303.

[14] 李龙清，宫雯，许永刚.基于G1法的煤矿企业信息化水平指标权重的确定[J].西安科技大学学报，2012，32(4):518-521.

[15] 刘建，郑双忠，邓云峰，等.基于G1法的应急能力评估指标权重的确定[J].中国安全科学学报，2006，16(1):30-33.

[16] 郭亚军.综合评价理论与方法[M].北京:科学出版社，2002：160.

[17] 王大庆，张鹏，郭龑，等.考虑相关性时LNG储罐泄漏模糊事故树定量分析[J].中国安全科学学报，2014，24(1):96-102.

[18] 何涛.轨道交通全电子化联锁系统安全技术研究与系统分析[D].兰州:兰州交通大学，2014.